喷动床最小喷动速度的计算颗粒流体力学数值模拟

金海安， 王东祥,2， 俞建峰,2

(1.江南大学 机械工程学院， 江苏 无锡 214122；2.江南大学 江苏省食品先进制造装备技术重点实验室， 江苏 无锡 214122)

喷动床具有结构简单，床内气固接触和颗粒混合特性良好等优点，已广泛应用于食品、化工、能源和轻工等领域[1-5]。喷动床有着特定的操作条件，当喷口表观气速达到最小表观喷动速度(以下均称最小喷动速度)，气体才可以突破床层形成喷动。最小喷动速度对喷动床的工艺设计与优化具有重要意义。Mathur等[6]提出的粗颗粒最小喷动速度经验关联式应用最为广泛。Monazam等[7]测量了普通平底喷动床的最小喷动速度，并基于Mathur-Gishler方程，建立了新的最小喷动速度关联式。任立波等[8]耦合CFD-DEM算法，研究了锥形喷动床内的气固流动行为，获得了稳定流态化阶段颗粒的时均速度分布规律。Duarte等[9]采用了双欧拉模型对锥型喷动床内的流体动力学特性进行了研究，其最小喷动速度模拟结果与文献试验值吻合较好。近些年，通过CPFD方法对颗粒相进行双重处理，节省了大量计算成本和时间，特别适合于复杂的多相流系统气固流动行为的模拟研究，在工业级流化装置模拟中逐渐成为主流[10-12]。课题组基于CPFD方法，建立二维锥形喷动床数值模型，数值模拟不同结构参数和操作参数床内的气固流动特性；分析喷口宽度、喷动气速以及颗粒特性对气固流动结构和最小喷动速度的影响，建立二维锥形喷动床最小喷动速度预测模型。

1 CPFD方法

CPFD结合了欧拉和拉格朗日方法的优点，将颗粒相既视为连续介质，也视为离散单元，按欧拉方法以流体网格上的应力梯度代替颗粒应力梯度，再插值到离散颗粒体上，并对颗粒相的其他属性使用拉格朗日法进行计算。CPFD将多个具有相同的物质属性、物理运动及化学变化的真实颗粒打包成一个计算粒子[13]，计算速度快，并且可以保证全局和局部物质输运守恒，可以更为快速准确地模拟复杂多相流系统的气固流动行为。

1.1 控制方程

对于气相，采用Navier-Stokes方程计算，湍流模型选择大涡模型(LES)，流体连续性方程和动量方程如下[14]：

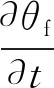
(1)

(2)

式中：uf为流体速度,m/s；θf为流体体积分数；ρf为流体密度,kg/m3；p为流体压强,Pa；F为流体与颗粒相间单位体积的动量交换率；g为重力加速度,m/s2。

对于颗粒相，假设每个颗粒的质量在时间上是恒定的(颗粒之间或流体之间没有质量传递)，但颗粒可具有一系列尺寸和密度，通过求解颗粒分布函数Φ(xp,up,ρp,Ωp,t)的输运方程来描述颗粒相的运动。其中xp为粒子位置；up为粒子速度，m/s；ρp为粒子密度，kg/m3；Ωp为粒子体积，m3。输送方程和颗粒的加速度[15]为：

(3)

(4)

式中：A是计算粒子加速度，m/s2；θp是颗粒体积分数；τp是颗粒的法向应力，Pa；Dp是曳力系数。

1.2 颗粒碰撞模型

CPFD中将多个真实颗粒处理成一个计算颗粒，对于真实颗粒间的碰撞无法逐一进行计算，通过引入碰撞模型来表征真实颗粒间的碰撞，将流体网格中的应力梯度插值到相应位置的颗粒上进行计算。颗粒碰撞时法向应力τp[16]为

(5)

式中：Ps为常数，Pa；θcp为颗粒堆积时的体积分数；β为常数，推荐值2～5；ε取值为10-7。

1.3 曳力模型

多相流中气固间的相互作用力通过曳力模型表征，常用的有Wen-Yu模型[17]、Ergun模型[18]和Gidaspow模型[19]等，其中Wen-Yu模型适用于稀相颗粒流，Ergun模型更多的适用于密相区域，Gidaspow模型结合了Wen-Yu和Ergun 2个模型的特点，其适用的浓度范围更为宽泛。喷动床内气固流动呈现稀相和密相混合状态，课题组选择Gidaspow模型计算曳力系数Dp：

Dp=D1,θp<0.75θcp;

(6)

0.75θcp<θp<0.85θcp; (7)

Dp=D2, 0.85θp<θp。

(8)

式中：D1和D2分别为Wen-Yu模型和Ergun模型的曳力系数。

2 模型参数

2.1 数值模型

如图1(a)所示，喷动床床高为800 mm，床体宽度为200 mm，厚度20 mm。喷动气入口底部是夹角为60°的V形结构，入口厚度为20 mm。模拟中入口厚度不变，入口宽度分别调整为20，15和10 mm以改变喷动气的进口尺寸。采用笛卡尔网格生成方法进行网格划分，如图1(b)所示。如果在网格中形成非常小的切割单元不能在模型中包含相关数量的计算粒子，则必须被移除或与附近较大的单元合并来维持模型稳定性。研究采用的颗粒直径为1.3～3.2 mm，床体宽度是床体厚度的10倍，床体厚度大于粒径的5倍，满足二维喷动床条件[20]，其呈现出的流动特性能较真实反应实际的气固流动。

采用网格数量为10 000，15 000和20 000进行网格无关性验证以检验合理的网格数量范围。从表1中可以看出，当网格数量超过15 000后，床体高度为50，100和200 mm处压力监测点的数值不再出现明显改变，即可保证计算结果的可靠性。为了更准确地模拟喷动床内颗粒的流动形态，底部锥形区域的网格进行了加密，有效网格数量为16 251。

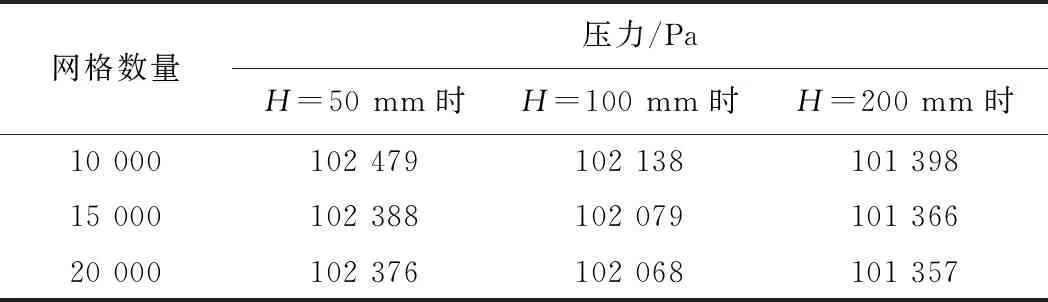
表1 网格无关性验证

2.2 模拟参数

以空气作为入射气体，所选固体物料为绿豆、小米和3种不同直径的玻璃珠，颗粒参数如表2所示。表3所示为模拟时相关参数的设置情况。采用升速法结合压降曲线得到最小喷动速度并对颗粒不同流动形态进行观察。

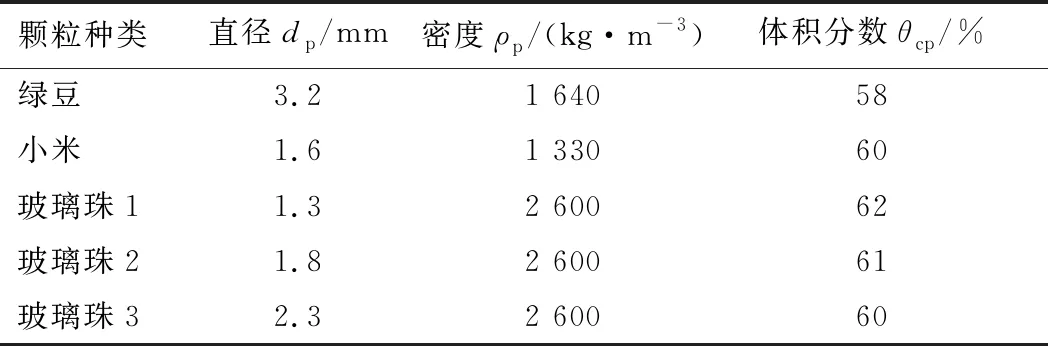
表2 颗粒物性参数

表3 模拟参数

3 结果与讨论

3.1 实验验证

根据Liu等[21]的实验数据对初始床高分别为50，75和100 mm的二维喷动床最小喷动速度进行模拟计算，填料为直径2 mm，密度2 380 kg/m3的玻璃珠，通过逐渐增加喷动气速引起的床层压降变化和具体床层流动形态来确定最小喷动速度。图2为表观气速Us=1.58 m/s时稳定喷动状态下二维喷动床的实验和模拟对照图，从图中可以看出两者在喷动结构上有着高度一致性。环隙区颗粒不断流入喷动区，最终在喷动区出口形成喷泉。模拟结果中喷泉区中颗粒相对较少的主要原因是CPFD方法是将多个真实颗粒“打包”成一个计算颗粒进行计算。

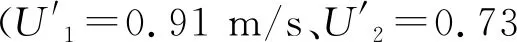
3.2 喷动结构

图4为Us=2.3Ums时喷动过程的模拟情况。t=0.0 s时，向喷动床内通入高速气体来推动物料上升；t=0.2 s时，床层中部形成一段大气泡状空腔，尺寸接近床层截面积，类似腾涌射流流动结构。主要原因是气速突然增大，推动物料整体上升，床层表面高度明显升高，气体需要运动距离增大，向四周渗透的气体增加，造成空腔范围增大。气体继续上升至突破床层后将携带的颗粒向四周抛洒，逐渐形成稳定的喷动区和喷泉区。可以看到环隙区颗粒缓慢向下运动至底部后被卷吸入喷动区随着入口高速气流上升，进行新的循环。

图5是喷动气速逐渐增大时床内流动结构的变化。当喷动气速小于最小喷动气速时，气体无法穿透床层，颗粒只能在床层内部形成射流区内进行循环。区别于图4中t=0.2 s时产生的大气泡，图5中Us=0.8Ums时形成的内部射流区较窄，在内部射流区顶端形成气泡继续上升并不断聚拢至床层表面破裂。随着喷动气速继续增加，气流突破床层后并形成喷泉。从图中可以明显看出喷泉的高度随着喷动气速增加而增加，当气体速度足够大时，大量颗粒被吹起布满整个床体，没有明显喷泉区界线，喷动床开始向气力输送床转变。

3.3 最小喷动速度的影响因素

3.3.1初始床高的影响

图6为喷口宽度为20 mm的条件下，初始床高和床宽的比值与最小喷动速度的关系。从图中可以看出在喷口宽度和床宽不变的条件下，不同填充材料的最小喷动速度都随着初始床高的增加而增加，并且在初始床高超过锥形体高度后，两者呈现出良好的正比关系。产生这种现象的原因主要有2个：一是因为初始床高的增加即初始填充物料的增加，气体在上升过程中需要吹起更多的颗粒，导致阻力增大，就需要更高的气速来克服阻力产生喷动；二是初始床高的增加使气体需要上升的距离变长，更多的气体在突破床层的过程中由喷动区向四周环隙区逸散，导致需要更多气体来产生喷动，使最小喷动速度增大。

3.3.2颗粒直径的影响

图7为颗粒直径与最小喷动速度的关系，在喷口宽度为20 mm的条件下，选用了1.3，1.8和2.3 mm的3种直径的玻璃珠作为填充物料。从图中可以看出最小喷动速度随着颗粒直径的增大而迅速增大。主要原因是由于同种密度的材料，颗粒直径增大，颗粒的表面积和体积比减小，导致相同质量的颗粒喷动所需气体的速度增加[22]。随着颗粒直径的增大，颗粒的终端速度相应增大也是最小喷动速度增大的一个原因。结合图6初始床高与最小喷动速度的关系可以看出同样的比例系数下颗粒粒径对最小喷动速度的影响远大于初始床高的影响。

3.3.3喷口宽度的影响

图8为喷口宽度与最小喷动速度的关系。在H0/Dt为1.4的条件下，喷口宽度为10，15和20 mm时，3种填充物料的最小喷动速度变化呈现出相同趋势。从图中可以看出随着喷口宽度增大，最小喷动速度逐渐增大。一方面是随着喷口宽度的增加，喷动区的平均宽度也逐渐增大，气体在上升过程中会卷吸更多的颗粒，需要更高的气速来克服其产生的阻力。另一方面，由于喷口宽度的增加，气体向环隙区的扩散量也在增加，导致气体携带的动能损失增大，需要更多的气体来弥补动能损失，导致最小喷动速度增大。

通过上述分析得到最小喷动速度受到初始床高、颗粒直径、颗粒密度和喷口宽度等影响。根据唐凤翔等[23],[24]54对最小喷动速度关联式的研究，可以写成下面的参数群形式：

(9)

结合不同操作条件下的模拟结果进行多元线性回归分析，确定系数a～e，得到最小喷动速度关联式为

(10)

图9(a)将最小喷动速度关联式的计算值与模拟值进行比较，从图中可以看出计算值与模拟值具有很高的吻合性；相关系数为0.98，标准误差为9.8%，吻合较好，相对误差在12.5%以内，该关联式对此类喷动床最小喷动速度的预测具有较高的准确性。图9(b)中将得到的最小喷动速度的关联式与其他学者的关联式进行对比，从图中可以发现在相同的条件下，所有关联式的预测值呈现相同趋势；相对误差大部分控制在30%以内，与Uemaki和Wang等[25-26]得到关联式预测值非常吻合，说明研究得到的关联式对于最小喷动速度的预测具有一定的可靠性。Zhong[24]52的关联式中考虑了流化气的影响，而Choi等[27]填充颗粒的粒径比差异较大，喷动床床体并非二维结构，导致了与关联式的预测值误差较大。

4 结论

课题组采用CPFD方法建立了二维喷动床数理模型，对最小喷动速度和气固流动结构进行数值模拟，考虑了操作参数和结构参数的改变对最小喷动速度和流动结构转变的影响，并通过对比文献实验数据验证了模型准确性，得到如下结论：

1) 随着喷动气速增加，床内将逐步呈现内部射流、鼓泡射流、喷动、稳定喷动和气力输送等流动结构，稳定喷动流动结构的发生需要喷动气速维持在一定范围内。

2) 最小喷动速度随着初始床高、颗粒粒径和喷口宽度增大而增大，通过增大喷动速度可克服颗粒产生的阻力和弥补气体携带动能损失；相对于喷口宽度，静止床高和颗粒直径对最小喷动速度影响较为显著。

3) 研究得到的二维锥形喷动床最小喷动速度关联式与已有二维经验关联式吻合较好，能够准确预测二维喷动床最小喷动速度，对于三维喷动床则存在一定误差。