多分支HQ管模型的传声损失分析
齐成婧,毛崎波
多分支HQ管模型的传声损失分析
齐成婧,毛崎波
(南昌航空大学飞行器工程学院,江西南昌 330063)
通过波动方程建立了多分支赫歇尔-昆克(Herschel-Quincke, HQ)管的传声损失模型,该模型可计算包含任意数量、不同管径和不同管长组合的HQ管模型。通过与前人的计算结果进行比较,验证了该方法的有效性。并通过数值计算,分析讨论了不同参数(如HQ管的长度和直径、HQ管分支数量)对多分支HQ管传声损失的影响。结果表明:在总横截面积相等的情况下,多分支HQ管吸声性能与单分支HQ管相同;改变管道的长度可以改变共振频率;比较频率平均传声损失,HQ管长度不统一的结构的声学特性优于长度统一的结构。
多分支HQ管;传声损失;数值计算
0 引言
赫歇尔-昆克(Herschel-Quincke, HQ)管是一种利用声波叠加干涉原理的简单可行的消声设备,能有效地阻止或减少噪声的传播。早期,戴根华等[1]研究了带旁通的无流动管道系统的声学性能,利用具体的数值计算证明了声能环流的存在和传声损失的频率特性。而后,朱之墀等[2]研究了有流动的管道中旁通管降噪的问题。Selamet等[3]将传统的HQ管延伸到管并联的结构,而且推导出了各分支HQ管的传递损失表达式。董为民等[4]针对单分支HQ管和串联HQ管及具有微穿孔、阻性材料内衬复合HQ管消声器进行了仿真计算和实验研究。Torregrosa等[5]研究了对传统的HQ管结构在有均匀气流场时,气流对结构消声性能和共振位置的影响。Liu等[6]对比了分别在有气流和无气流时,主管道和HQ管管道的角度和直径变化对声学性能的影响。Howard等[7]改变支管与主管的接口处形状,通过实验分析不同接口形状对降噪性能的影响。苏吉益等[8]通过实验分析HQ管不同主管与旁通管的长度和面积比,以及不同构型的HQ管对降噪效果的影响。
HQ管降噪技术已广泛应用于航空、船舶、车辆的风扇、发动机进排气等的噪声控制。Burdisso等[9]和Hallez等[10]在涡扇发动机的入口处安装HQ管,将HQ管应用于航空发动机的噪声控制,也有学者将HQ管应用在汽车进气口降噪系统中[11]。Zhu等[12]利用HQ管提出了一种新型的半主动消声装置,有效地控制了汽车内排气管道的低频噪声。Sagar等[13]将HQ管应用于H型连接的双重消声器的两边,验证了设置H型连接对高效消声器的有效性。Tristan等[14]将纸折成螺旋管状,插入HQ管中,增加其吸声特性,并通过实验证明了优化HQ管的潜力。杨帆[15]对HQ管用作液压脉动衰减器的滤波特性进行了研究,验证了HQ管用于液压系统压力脉冲衰减的可行性。Zhan等[16]进一步提出通过HQ管模型解决往复式压缩机中的不定常流动。
目前的研究主要集中于单分支HQ管的消声性能的影响和实验仿真,而针对于多分支HQ管结构模型的分析研究较少。HQ管的消声特性不仅与反相干涉原理有关,也与主管道和旁管道的几何尺寸密切相关。因此有必要对多分支HQ管进行相关分析研究。本文从声传播解析公式出发,利用传递矩阵推出多分支HQ管结构模型的传声损失计算公式,与前人的计算对比,验证了公式的有效性。最后举例计算并列5个分支HQ管结构的传声损失,研究讨论传声损失的频率特性与HQ管管道长度及直径的关系。
1 理论分析
在管道传播噪声控制中,噪声可以分为平面声波和高阶模态声波,当管道入射声波的频率小于第一个高阶模态的截止频率时,则噪声以平面声波传播。假设管道的入射声波频率远远低于管道传声的截止频率,声波在任意管道内以平面波形式传播,则声压表达式为[17]

相应的质点振动速度为



图1所示为多个HQ管分支的简单模型且为无气流的状态。利用传递矩阵来计算结构的传声损失。声波从上游管道进口,经主管和多个平行HQ管道分支,从下游管道出口流出,假设出口端无反射,则整个管道模型的传递函数为
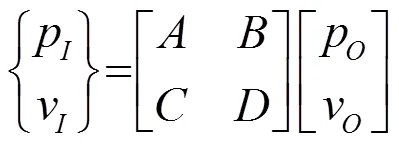
图1中I、O分别表示多HQ管分支上游和下游的连接点,则、和、分别为I、O处的声压和体积速度。
可以得到任意管道的传递矩阵函数
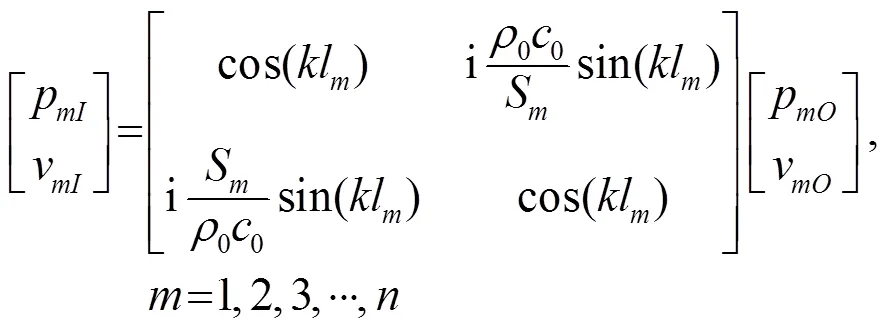
根据声压连续和体积速度连续的边界条件,在、处应满足以下条件:
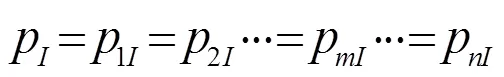



因为声压连续,求得任意一根HQ管入口处的声压即可得到点声压,将=1代入式(5),并结合式(6)、(7)可解得:

根据式(5)和式(10)可解得任意管出口端的体积速度:

将式(11)代入(9),得到点处的体积速度:
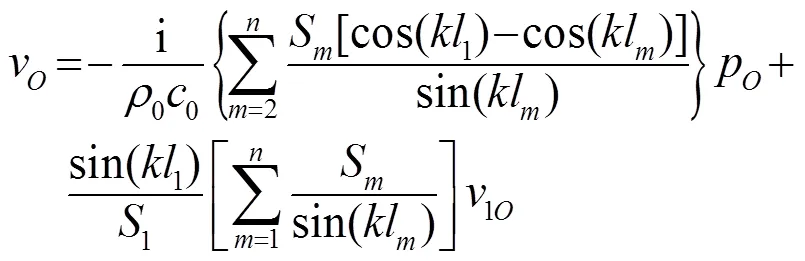

由式(13)对比式(4)可知:


同理,根据式(7),将式(11)代入(5)可得:

将式(16)代入(8),得到:


对比式(18)、式(4)可知:
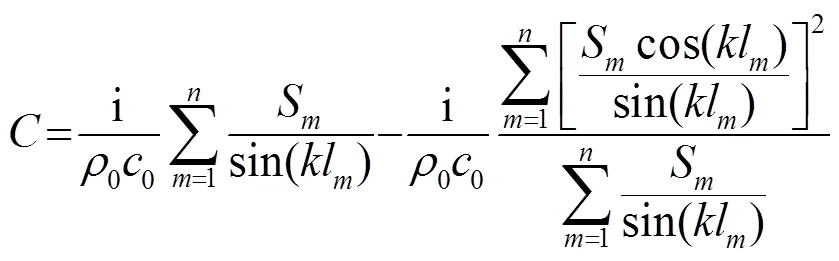
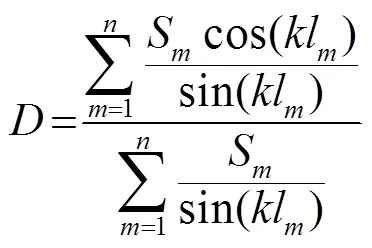
综上所述,式(14)、(15)、(19)、(20)的组合完整地表达了如式(4)所示的多分支HQ管道的传递函数。
消声量的大小作为消声器声学性能评价的主要指标之一,可以用传声损失来表征,且受声源与环境的影响较小[19]。因此,传声损失作为HQ管性能分析计算和结构设计的主要依据,具有重要意义。传声损失是HQ管上游进口噪声声功率级和下游出口噪声声功率级的差值,要考虑到声波的相位差和声强,可以通过旁管和主管的长度及面积来调节。
若带点粒子的初速度不为零,因初速度方向与电场线平行,即带电粒子所受合外力方向和速度方向相同,那么带电粒子将做匀加速直线运动或匀减速直线运动,同样可根据动能定理得出:
根据文献[18]可知,传递矩阵计算传声损失的表达式为
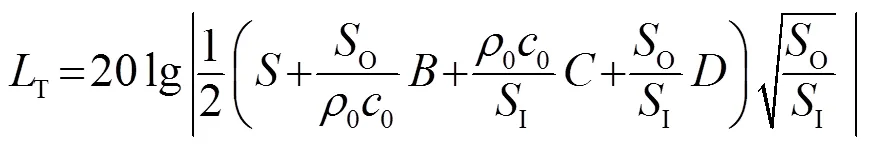

由式(22)可知,产生共振的条件为

当满足式(23)时,发生共振,HQ在发生共振时的传声损失达到最大。

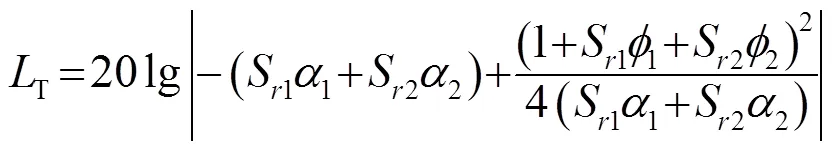
其中:

由式(24)、(25)所得到的传声损失公式与前人分析推导出的单分支HQ管结构传声损失相同[4]。
对于单分支HQ管,共振条件为

将式(25)代入式(26)中,可得:

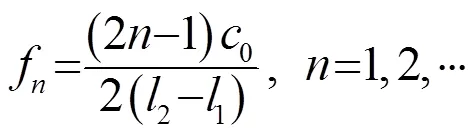
当所有HQ管的长度与主管相等时,模型可等效于单节扩张室消声器,则式(22)可进一步化简为

2 数值分析



图2 单分支HQ管传声损失和膨胀室传声损失比较(d1=0.05 m)
当管道横截面积相同时,由多HQ管共振条件式(27)求得,图2中显示的两次共振频率分别为428.75 Hz和1 286.25 Hz。与文献[3]的结果一致,这证明本文方法是可行的。
2.1 多HQ管模型的管径对传声损失的影响

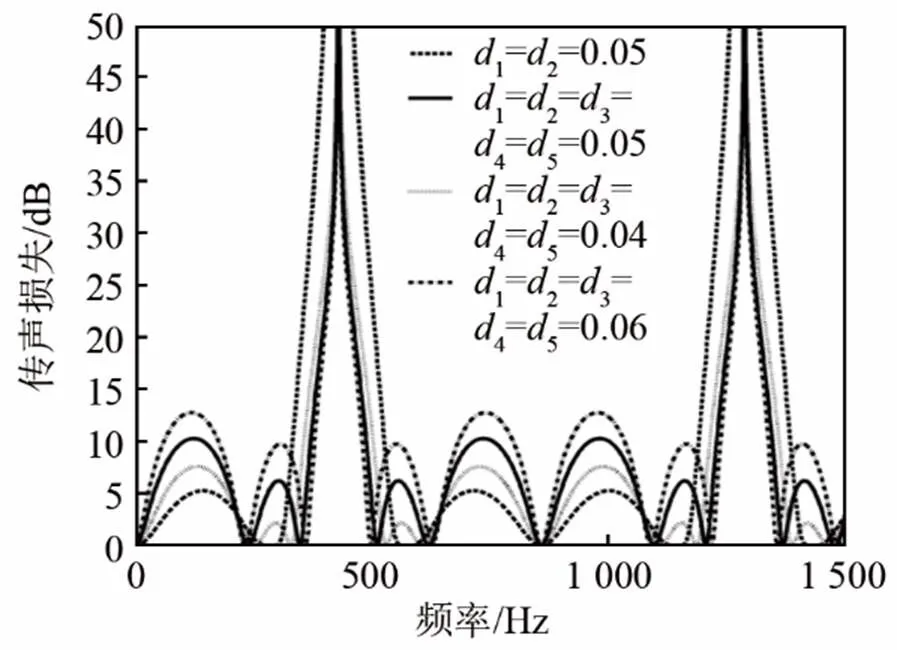
图3 同等改变各HQ管直径时多分支结构传声损失的变化
Fig.3 The acoustic transmission loss change of the multi-branch structure when the diameter of each HQ tube changes equally


综上所述,HQ管长度不变时,传声损失的大小与HQ管的总横截面积有关,总横截面积越大,传声损失越大,反之,总横截面积越小,传声损失越小。
2.2 管长对传声损失的影响


图4 同等改变各HQ管长度时多分支结构传声损失的变化
由表1可再一次证明,HQ管的消声性能优于膨胀管的消声性能。从表1和图4、图5可以发现,当保持HQ管的管径不变时,改变HQ管长度,结构的共振频率将发生相应改变,各HQ管不同长度时的频率平均传声损失要高于同等长度变化时的频率平均传声损失。所以,当通过多分支HQ管实现宽频吸声时,应该把管长设计为不同长度。


图5 非同等改变各HQ管长度时多分支结构传声损失的变化(l1=0.7 m, l2=0.75 m, l3=0.8 m, l4=0.85 m, l5=0.9 m)

表1 各HQ管长度改变时多分支结构在不同频率的平均传声损失
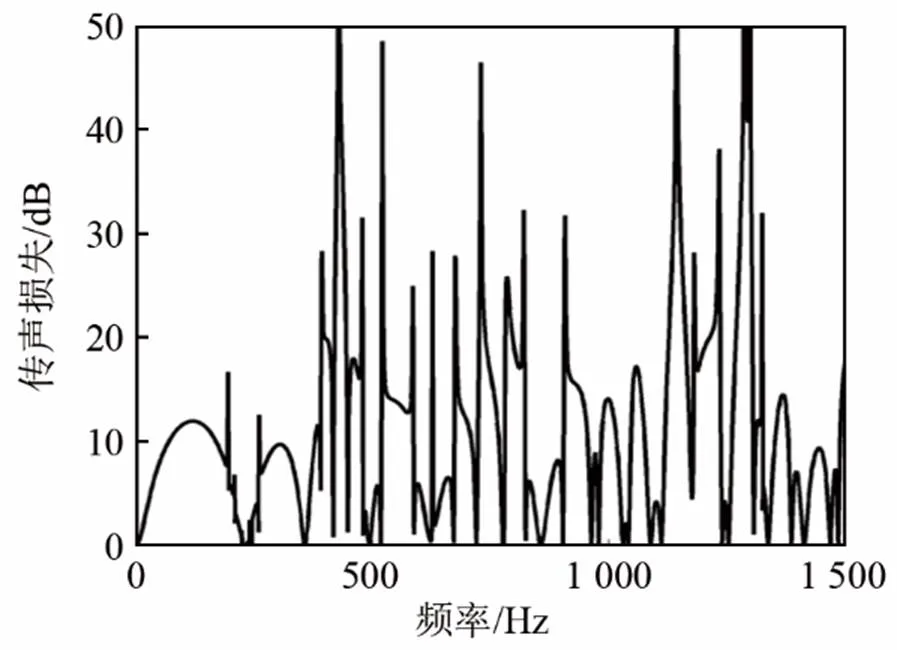
图6 六分支HQ管结构的传声损失频率特性
由图6结合共振条件公式(23)可知,管道数量越多,共振也随之增加,导致多分支HQ管结构的传声损失的频率特性更加复杂。
3 结论
基于传递矩阵法分析推导出多分支HQ管模型传声损失的公式和共振条件公式,此公式可以计算任意数量、任意管长管径的HQ管模型。利用MATLAB进行数值计算,计算了传统单分支HQ管的传声损失,并以5个HQ管分支的结构为例,分析其频率特性。结果表明,HQ管的数量越多,其传声损失的频率特性越复杂,同时,HQ管直径和长度的改变对其消声特性有很大影响。当保持HQ管长度不变时,若保持所有HQ管横截面积的总和不变,数量和直径的变化不影响传声损失;若总横截面积增大,则传声损失也增大;当保持HQ管直径不变时,改变其管长可使其共振频率发生改变。实际应用中可以结合实际降噪要求,合理配置HQ管的数量和几何参数,使其可以同时达到所需的最佳消声效果和最佳结构。
[1] 戴根华, 田瑞, 李鹭, 等. 带旁通的管道中的声能流及传声损失—Ⅰ: 理论分析[J]. 声学学报, 1995, 22(4): 244-249.
DAI Genhua, TIAN Rui, LI Lu, et al. Acoustic energy flux and transmission loss in a duct with a by-pass, part I: theoretical analysis[J]. Acta Acustica, 1995, 22(4): 244-249
[2] 朱之墀, 田瑞. 流动管道内利用旁通管道反声降噪研究[J]. 声学学报, 1997, 22(1): 1-10.
ZHU Zhixi, TIAN Rui. A study of noise reduction by anti-sound bypass in ducts with flow[J]. Acta Acustica, 1997, 22(1): 1-10.
[3] SELAMET A, EASWARAN V. Modified Herschel-Quincke tube: Attenuation and resonance for n-duct configuration[J]. Journal of the Acoustical Society of America, 1997, 102(1): 164-169.
[4] 董为民, 李功宇, 尹红. HQ管反声消声器的仿真分析及实验研究[J]. 噪声与振动控制, 2004, 24(2):34-37.
DONG Weimin, LI Gongyu, YIN Hong. Numerical simulation and experimental study of HQ tube attenuator[J]. Noise and Vibration Control, 2004, 24(2): 34-37.
[5] TORREGROSA A J, BROATCH A, PAYRI R. A study of the influence of mean flow on the acoustic performance of Herschel–Quincke tubes[J]. J. Acoust. Soc. Am., 2000, 107(4): 1874-1879.
[6] LIU X G, YIN C C. A study of the Herschel-Quincke tube concept[J]. Advanced Materials Research, 2011, 199-200: 1024-1030.
[7] HOWARD C Q, CRAIG R A. Noise reduction using a quarter wave tube with different orifice geometries[J]. Applied Acoustics, 2014, 76(1): 180-186.
[8] 苏吉益, 施琳. 旁通管的应用与降噪性能研究[J]. 吉林化工学院学报, 2017, 34(5): 81-84.
SU Jiyi, SHI Lin. An applied study of noise reduction by anti-sound using bypass[J]. Journal of Jilin Institute of Chemical Technology, 2017, 34(5): 81-84.
[9] BURDISSO R A, GERHOLD C H. Fan noise control using Herschel-Quincke resonators on a production turbofan engine[J]. J. Acoust. Soc. Am., 2002, 111(5): 2452-2453.
[10] HALLEZ R F. Investigation of the Herschel-Quincke tube concept as a noise control device for turbofan engines[D]. Blacksburg, Virginia Polytechnic Institute and State University, 2001.
[11] 谢志清, 李泽状, 王伟伟. 汽车进气系统1/4波长管的设计与应用[J]. 装备制造技术, 2015(7): 220-222.
XIE Zhiqing, LI Zezhuang, WANG Weiei. Design and application of 1/4 wave resonating pipe for vehicle air induction system[J]. Equipment Manufacturing Technology, 2015(7): 220-222.
[12] ZHU Y W, ZHU F W, ZHANG Y S, et al. The research on semi-active muffler device of controlling the exhaust pipe’s low-frequency noise[J]. Applied Acoustics, 2017, 116: 9-13.
[13] SAGAR V, MUNJAL M L. Analysis and design guidelines for fork muffler with H-connection[J]. Applied Acoustics, 2017, 125: 49-58.
[14] TRISTAN C, EMMANUEL G. Innovative origami-based solutions for enhanced quarter-wavelength resonators[J]. Journal of Sound and Vibration, 2018, 434: 379-403.
[15] 杨帆. Herschel-Quincke管用作液压脉动衰减器的滤波特性研究[J]. 液压与气动, 2018(8): 81-85.
YAN Fan. Filtering Characteristics of Herschel-Quincke tube used as hydraulic noise suppressor[J]. Chinese Hydraulics and Pneumatics, 2018(8): 81-85.
[16] ZHAN L, XU E L, JIA W G, et al. Improvement of one-dimensional gas dynamic model for pulsation prediction in reciprocating compressor systems[J]. Energy Procedia, 2018, 152: 137-142
[17] MAO Q B, PIETRZKO S. Control of noise and structural vibration[M]. London: Springer, 2013.
[18] MUNJA M L. Acoustics of Ducts and Mufflers[M]. Chichester: Wiley, 2014.
[19] 季振林. 消声器声学理论与设计[M]. 北京: 科学出版社, 2015.
JI Zhenlin. The theory and design of muffler[M]. Beijing: Secience Press, 2015.
Analysis of the acoustic transmission loss of multi-branch HQ tube structure
QI Chengjing, MAO Qibo
(School of Aircraft Engineering, Nanchang Hangkong University, Nanchang 330063, Jiangxi, China)
The acoustic transmission loss model of multi-branch HQ tube is established based on the wave equation. The proposed model can be used to calculate the HQ tube model with any number of branches, different diameters and/or lengths. The effectiveness of the method is verified by comparison with previous calculations. Then, the influence of different physical parameters, such as the length and diameter of HQ tube and the number of HQ tube branches, on the acoustic transmission loss of multi-branch HQ tube is analyzed and discussed in detail. The calculation results show that the acoustic transmission loss of multi-branch HQ tube is the same as that of a single-branch HQ tube when the total cross-section areas of both are equal; and changing the length of the HQ tube can change its resonance frequency. By comparing the average acoustic transmission loss in frequency domain, it can be seen that the acoustic performance of the HQ tube structure with different lengths is superior to that with united length.
multi-branch HQ tube; acoustic transmission loss; numerical calculation
TB535.2
A
1000-3630(2020)-02-0224-06
10.16300/j.cnki.1000-3630.2020.02.017
2018-12-10;
2019-01-24
国家自然科学基金(11464031, 51265037)、江苏省六大人才高峰(KTHY-036)、江西省自然科学基金(20192BAB206024)资助项目
齐成婧(1995-), 女, 湖南株洲人, 硕士研究生, 研究方向为噪声与振动控制。
毛崎波,E-mail: qbmao@nchu.edu.cn

