摄动开普勒问题形式化建模与验证

王国辉，许京然，刘永梅，施智平，关 永

1(首都师范大学 信息工程学院,电子系统可靠性技术北京市重点实验室，北京 100048)2(首都师范大学 北京成像理论与技术高精尖创新中心，北京 100048)3(北京城市学院 信息学部，北京 101399)4(首都师范大学 电子系统可靠性与数理交叉学科国家国际科技合作示范型基地，北京 100048)

1 引 言

人造地球卫星在地球引力的作用下沿闭合轨道绕地球做周期性运行.当地球是一个质量分布均匀的标准球体时，卫星的轨道应该为标准的椭圆形，并服从开普勒三大定律.然而，地球表面高低起伏，地球内部结构复杂，使得地球引力在空间分布不均.人造地球卫星在地球引力场的作用下，其运行轨道发生较为复杂的变换，产生摄动问题[1].因此，摄动开普勒问题在卫星轨道分析研究过程中得到广泛应用.该领域对安全性与可靠性要求非常严格，微小的错误将导致灾难性后果.

早在1920年Levi-Civita就提出二维谐振子描述平面开普勒问题[2].1964年Kustaanheimo和Stiefel提出四维谐振子描述空间开普勒问题[3].这两种类型将开普勒问题中的微分方程转化为线性微分方程且都是可行的.1995年Vivarelli和Vrbik提出了利用四元数解决该问题的可行性[4].直到2006年Waldvogel利用四元数合理的解决了该问题并给出了推导方法与过程.从二维复数到三维四元数的代数转换，是一次突破性进展[5].但是上述方法在解决卫星摄动开普勒问题的建模与分析过程中涉及到矢量代数、旋量代数、复数、四元数等多种不同的代数系统，在各个代数系统相互转换过程中极易引入错误.2008年哈尔滨工业大学方茹等[6]提出了利用几何代数解决摄动开普勒问题.该方法利用几何代数将摄动开普勒问题的建模与分析统一到相同代数结构中，同时把摄动开普勒方程转换成旋量方程来求解，有效避免奇点的同时弥补传统分析方法的不足.

由于上述建模与分析方法主要依靠纸笔演算、数值计算和计算机代数系统.纸笔演算的方法耗时耗力，容易引入人为错误；计算机数值计算方法由于计算机无法精确表示实数，数值计算不能给出精确的结果；计算机代数系统在边界条件、奇异表达简化方面的处理具有缺陷，此外庞大的符号计算程序不能排除程序漏洞的存在[7].相对于传统的建模与分析方法，基于定理证明的形式化方法采用严格的高阶逻辑描述数学问题的属性和规范，以公认的逻辑公理和推理规则为基础构建形式化建模和验证过程，在安全攸关的系统设计中具有很大优势.

中国科学院李洪波[8]在2002年首次提出应用Clifford代数自动证明共形几何模型，创立了高效的几何计算和推理新方法.2013年Harrison等曾使用HOL Light对几何代数的基本内容，主要包括多重矢量和基矢量做出了形式化定义，完成了几何代数核心运算和部分性质的证明[9].2016年马莎等[10]完成了共形几何代数的高阶逻辑形式化验证工作，为几何代数定理证明做了铺垫.2018年李黎明[11]在HOL Light定理证明器中构建了几何代数的高阶逻辑定理库，为摄动开普勒问题的形式化建模与分析提供了必要条件.本文通过定理证明的方法对基于几何代数的摄动开普勒问题进行形式化建模与分析，并给出严格的高阶逻辑推理，从而最大程度确保数学模型的正确性和分析方法的可靠性.

2 几何代数基础及其形式化

几何代数是由Grassmann 代数和Clifford 代数发展而来的，能够统一多种代数结构到同一框架下，从而避免多种代数系统之间相互转换的问题.利用几何代数中几何体、几何关系和几何变换描述不依赖坐标的优点，可以将描述卫星轨道运动的摄动开普勒方程转化为线性、正则旋量方程，即KS方程[12].

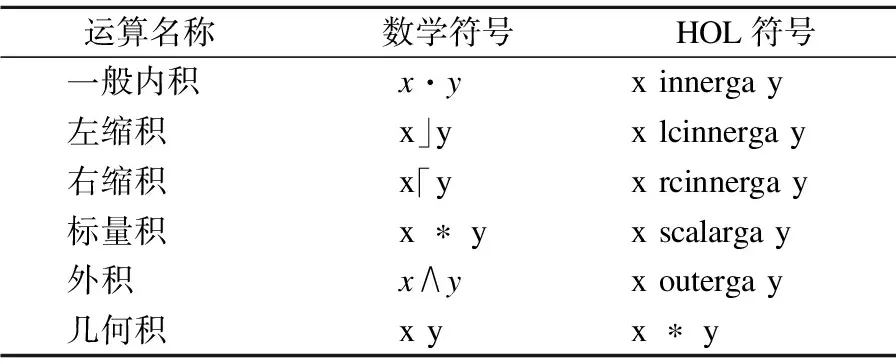
表1 几何代数基本运算在定理证明库中的表示Table 1 Representation of the basic operations of geometric algebra in the theorem proving library

2.1 几何代数基本运算及其性质的形式化

几何代数建立在多重向量空间上，其基本元素为多重向量.几何代数运算主要包括内积、外积和几何积.在使用过程中，内积还分为一般内积、左缩积、右缩积和标量积四种.在HOL Light定理证明库中，几何代数基本运算如表1所示.几何代数基本运算不依赖研究对象的坐标系统，只与坐标基之间的相对位置有关.其运算规则符合双线性、结合律和分配律等基本性质，有效的统一了标量运算、矢量运算、维度运算和几何运算.

本文以一般内积为例简要介绍其定义及性质的高阶逻辑形式化描述.其他运算的定义与性质可参见几何代数的高阶逻辑定理证明库1.

定义1.几何代数一般内积

|- x innerga y：real^(P，Q，R)geomalg =

Productga(s t.if s={} / t={} /

～(s SUBSET t)/～(t SUBSET s) then & 0

else --(& 1)pow CARD {i，j | i IN 1..(pdimindex(：P)

+pdimindex(：Q)+pdimindex(：R))/

j IN 1..(pdimindex(：P)+pdimindex(：Q)+

pdimindex(：R))/ i IN s / j IN t / i > j} *

--(& 1)pow CARD((pdimindex(：P)+

1..pdimindex(：P)+pdimindex(：Q))

INTER s INTER t)* & 0 pow

CARD((pdimindex(：P)+pdimindex(：Q)+

1..pdimindex(：P)+pdimindex(：Q)+

pdimindex(：R))INTER s INTER t))x y

其中real^(P，Q，R)geomalg为几何代数基本元素多重向量的类型.

性质1.一般内积双线性性质

|- bilinear f =(!x.linear(y.f x y))/

(!y.linear(y.f x y))

其中linear为线性性质描述.

|-linear(f：real^M->real^N)=

(!x y.f(x+y)= f(x)+f(y))/〗(!c x.f(c*x)= c * f(x))

性质2.一般内积结合律性质

|- !x y z.op x(op y z)= op(op x y)z

其中op为二元操作符.

2.2 位置矢量与旋量

由几何代数基础知识可知，欧式空间内的旋转和伸缩变换满足如公式(1)所示的欧式空间内矢量与几何空间内的旋量或四元数之间的关系.

(1)

2.3 多重向量微分形式化

基于几何代数理论的卫星摄动KS方程涉及卫星与地球的位置、速度和加速度的关系.因此需要构建多重向量微分及其基本定理的形式化，为开展摄动开普勒问题的形式化工作做准备.Maggesi等[13]在HOL Light系统中完成了向量函数的微分，本文以此为基础，实现多重向量微分形式化.

定义2.多重向量函数f与微分函数f′之间的关系

|-(f has_ multivector _derivative f′)net <=>

(f has_multivector_derivative(x.drop(x)% f′))net

定义3.多重向量函数f在某点进行向量微分的函数值

|- multivector _derivative(f：real^1->(P，Q，R)geomalg)net=@f′.(f has_multivector _derivative f′)net

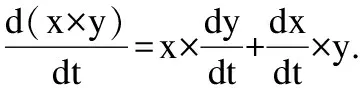
|- !x y：real^1->real^(′3，′0，′0)geomalg x′ y′ t.

(x has_ multivector _derivative x′)(at t)/

(y has_ multivector _derivative y′)(at t)

==>(( .(x t inner y t))

has_multivector _derivative

((x(t)inner y′)+x′ inner y(t)))(at t)

|-!x y：real^1->real^(′3，′0，′0)geomalg x′ y′ t.

(x has_ multivector _derivative x′)(at t)/〗(yhas_ multivector _derivative y′)(at t)

==>(( .(x t outer y t))

has_ multivector _derivative

((x(t)outer y′)+x′ outer y(t)))(at t)

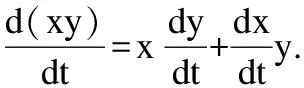
|-!x y：real^1->real^(′3，′0，′0)geomalg x′ y′ t.

(x has_ multivector _derivative x′)(at t)/〗(y has_ multivector _derivative y′)(at t)

==>(( .(x t * y t))

has_ multivector _derivative

((x(t)* y′)+x′ * y(t)))(at t)

上述三个多重向量函数运算微分的性质形式证明，为卫星摄动开普勒问题形式化建模奠定了基础.

3 卫星摄动开普勒问题形式化建模

3.1 惯性坐标系中摄动开普勒方程形式化

人造地球卫星在三维欧式空间的惯性坐标系中，卫星与地球之间有微小且不可忽略的摄动力，在微小的摄动力f的作用下，系统的摄动开普勒方程可以表示为方程(2).

(2)

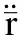
定义4.惯性坐标系中摄动开普勒方程形式化描述

|-multivector_derivative((multivector_derivative

(rotation_t r)(at t))(at t)=

((-k：real^1)*(r_position q t)/

norm(r_position q)pow & 3)+

(f：real^1->real^(′3，′0，′0)trip_fin_sum)

其中变量rotation_t r表示的是天体的矢量位置，它是一个与时间t有关的矢量函数；f是一个与时间t有关的多重向量函数；multivector_derivative f(at t)表示函数f对时间t的微分.k是一个实数，即公式(1)中的变量μ.

3.2 基于几何代数的摄动开普勒方程形式化

利用几何代数相关理论，可以将摄动开普勒方程转换为运动的旋量方程，记为KS方程.该方程形式简单，计算方便，同时能够有效消除引力位奇异点1/r，如方程(3)所示.

(3)

定义5.基于几何代数的摄动开普勒方程形式化描述

|-& 2 % multivector_derivative

((multivector_derivative q)(at s))(at s)-(E_DEF q t k)*(q t)=q t*r_position u t *

(f：real^1->real^(′3，′0，′0)trip_fin_sum)

其中开普勒能量E定义6所示.

定义6.开普勒能量

|-E_DEF(q：real^1->real^(′3，′0，′0)geomalg)(t：real^1)(k：real)

=(& 2 %

((conjugation(multivector_derivative q(at t))*

(multivector_derivative q(at t)))MYMMYM {})- k)

/norm(r_position q t)

4 卫星摄动开普勒问题形式化验证

本小节将利用定理证明库中已有的和补充的定义、定理对基于几何代数的摄动开普勒方程进行形式化推导.根据能量守恒原则，证明上述两种摄动开普勒问题建模分析方法的等价性.从而验证了基于几何代数的摄动开普勒方程的正确性与完备性.

4.1 地球与卫星相对位置矢量形式化定义

在欧式惯性坐标系中，地球与人造地球卫星中心相对位置矢量关系满足公式(4)：

(4)

其中u为采用几何代数系统中多重向量的四元数表示，u+为u的共轭.

定义7.地球与卫星相对位置矢量形式化

|-r_position(q：quat)=

(geomalg_300_quat q)* mbasis{1} *

conjugation(geomalg_300_quat q)

其中，quat为四元数类型.conjugation(u)表示u的共轭.e1是一个矢量基，用mbasis{1}表示.geomalg_300_quat表示四元数表示与多重向量表示的转换，其形式化定义如定义7所示.

定义8.四元数与多重向量转换形式化定义

|-geomalg_300_quat(q：quat)=

(Re q)% mbasis{} +(Im1 q)% mbasis{2，3} +

(Im2 q)% mbasis{1，2} +(Im3 q)%

(--(mbasis{1，3}：real^(′3，′0，′0)geomalg))

4.2 地球与卫星相对位置形式化相关定理

由地球与人造地球卫星中心相对位置矢量关系公式(4)可得关系式(5)：

(5)

定理1.地球与卫星相对位置标量化

|-!q：quat.norm(r_position q)=

(norm(geomalg_300_quat q))pow 2

其中，norm表示矢量取模.

为了证明定理1的成立，需要引入两个引理.即引理1位置矢量与多重矢量共轭的关系和引理2多重矢量与其共轭乘积的交互性.首先，用重写策略(REWRITE_TAC)将定理1中的r_position和geomalg_300_quat定义展开.其次，运用化简策略(SIMP_TAC)并结合HOL Light向量库中的相关定理对目标进行化简.最后，将定理目标推导为实数相等，并应用实数推导自动策略(REAL_ARITH_TAC)完成证明.

引理1.位置矢量与多重矢量共轭关系

|-!q：quat.norm(r_position q)% mbasis{}=

geomalg_300_quat q *

conjugation(geomalg_300_quat q)

引理2.多重矢量与其共轭积的交互性

|-!q：quat.conjugation(geomalg_300_quat q)*

geomalg_300_quat q=

geomalg_300_quat q *

conjugation(geomalg_300_quat q)

4.3 基于几何代数摄动开普勒方程形式化推导

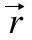
(6)

在形式化推导验证过程中，直接证明公式(6)成立相对复杂，所以先由多重向量的共轭性质(u+)+=u去证明等式(7).

(7)

|-!q′ q：quat.

((geomalg_300_quat q′ * mbasis{1} *

geomalg_300_quat(cnj q))$${1，2，3}=& 0 )

==>conjugation(geomalg_300_quat q′*mbasis{1} *

geomalg_300_quat(cnj q))=

geomalg_300_quat q′*mbasis{1}*

geomalg_300_quat(cnj q)

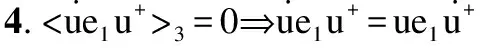
|-!q′ q：quat.((geomalg_300_quat q′*mbasis{1}*

geomalg_300_quat(cnj q))$${1，2，3}=& 0 )

==>geomalg_300_quat q′*mbasis{1}*

geomalg_300_quat(cnj q)=

geomalg_300_quat q*mbasis{1}*

geomalg_300_quat(cnj q′)

根据引理3和引理4可以把公式(6)化简，如公式(8)所示.

(8)

其高阶逻辑形式化表示如定理2所示.

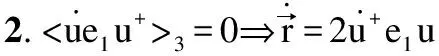
|-!q′：quat q：real^1->quat t：real^1.

((geomalg_300_quat q′*mbasis{1}*

geomalg_300_quat(cnj(q t)))$${1，2，3}=& 0 /〗((q)has_multivector_derivative q′)(at t))

==>(( .(r_position(q t)))

has_multivector_derivative

(& 2 %(geomalg_300_quat q′*mbasis{1}*

geomalg_300_quat(cnj(q t)))))(at t)

公式(8)左右两边同乘e1u，再对时间t求导，可得公式(9).

(9)

其形式化描述为定理3.

|-!(q：real^1->real^(′3，′0，′0)geomalg)

(s：real^1->real^(′3，′0，′0)trip_fin_sum)(t：real^1).

& 2 % multivector_derivative((r_position q t)*

(multivectorr_derivative q(at t)))(at t)=

& 2 / norm(r_position q t)*

multivector_derivative(

(multivector_derivative q)(at s))(at s)

此时可以得到关于u对s的二次微分，如公式(10)所示.

(10)

(11)

为了证明公式(11)成立，在逻辑推导过程中仍需引入dt=rds表示t与s的关系，用引理5表示其形式化描述.

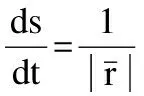
|-!(q：real^1->real^(′3，′0，′0)geomalg)(t：real^1)

(s：real^1->real^(′3，′0，′0)trip_fin_sum).

multivector_derivative s(at t)=

& 1 / norm(r_position q t)

通过上述推导，可以获得地球与人造地球卫星摄动开普勒问题的几何代数高阶逻辑模型，并且形式化证明了几何代数方法构建卫星摄动开普勒问题数学模型的正确性.

4.4 摄动开普勒问题几何代数模型与惯性坐标模型等价性证明

根据基于几何代数的摄动开普勒方程公式(2)可知，公式(11)满足摄动开普勒问题的旋量方程，根据能量守恒原则，可证如下公式(12)成立，

(12)

公式(12)可形式化为定理4，即开普勒能量守恒性质.

定理4.开普勒能量性质

|-!(q：real^1->real^(′3，′0，′0)geomalg)(t：real^1)

(k：real).E_DEF q t k =

(norm(multivector_derivative(r_position q)

(at t))pow 2 / & 2)-k/norm(r_position q t)

为了证明定理4的成立，需要证明开普勒能量引理，即引理6.

引理6.开普勒能量引理

|-!(q：real^1->real^(′3，′0，′0)geomalg)(t：real^1).

norm(r_position q t)*

(norm(multivector_derivative(r_position q)

(at t))pow 2)= & 4*norm

(multivector_derivative q(at t))pow 2

通过引理6的证明我们可以得到开普勒能量在几何代数下的形式化描述.定理4以开普勒能量守恒为形式化验证的最终目标.其证明过程主要借助上文提到的定义、引理和定理，运行重写、化简和自动求解等策略组合实现逻辑推导.从而证明摄动开普勒问题几何代数模型与惯性坐标模型具有等价性.

本小节的重点是将摄动开普勒旋量方程的形式化建模与验证.经过过严密的高阶逻辑形式推导，最大程度确保基于几何代数的摄动开普勒问题数学模型的正确性和分析方法的可靠性.

5 结 论

几何代数系统能够将多种代数系统统一在同一个代数系统中，避免了代数系统之间转换问题，有效的提高了卫星摄动开普勒问题分析的可靠性.本文以几何代数为数学基础，在高阶逻辑定理证明器HOL Light中建立摄动开普勒方程逻辑模型，对摄动开普勒问题进行了形式化分析与验证.由于解决摄动开普勒问题的需要，本文首先补充了几何代数基本运算微分性质定理；其次完成从欧式空间到几何代数空间的转换关系进行形式化；再次形式化证明多重向量的线性性质、共轭性质以及共轭的线性性质；最后采用高阶逻辑对基于几何代数的卫星摄动开普勒问题的数学模型进行形式化建模与推导，从而最大程度确保数学模型的正确性和分析方法的可靠性.

此外，摄动开普勒问题不仅应用于研究卫星轨道和姿态运动，也是研究两个带电粒子的运动方程基础，在测试物理理论和测量自然常数的模型系统中发挥了重要作用.因此下一步工作将围绕基于几何代数理论的微观世界粒子运动方程的形式化建模与验证展开.