一种最优粒子逐维变异的粒子群优化算法

罗 强,季伟东,徐浩天,孙小晴

(哈尔滨师范大学 计算机科学与信息工程学院,哈尔滨 150025)

1 引 言

PSO(Particle Swarm Optimization)算法[1]是由Kennedy和Eberhart通过对鸟群捕食过程中迁徙及群居行为的模拟,于1995年提出的一种群智能算法,该算法有简单易实现、参数少、对优化问题无连续性要求等优点,目前广泛运用于多个科学及工程实践领域.可是粒子群算法存在一系列问题,比如容易陷入局部最优、收敛速度慢、精度低等.针对这些问题很多学者以不同方式对粒子群算法进行优化,其中变异策略是一个优化热点,具有代表性的是柯西变异.

分析PSO算法公式可知,粒子前期飞行轨迹受自身的飞行经验(个体最优)以及全局最优信息影响,后期收敛于全局最优.这就说明有一个更优的全局最优信息点,将能引导粒子朝向更好的解空间飞行.为了得到一个更好的全局最优点信息,Wang等[2]提出了HPSO算法,通过对最优粒子进行多次柯西变异实现位置的更新.该方法能增加跳出局部最优的概率,加强全局搜索能力,且能加快收敛速度.

反向学习(Opposition-Based Learning,OBL)是Hamid R.Tizhoosh等[3]于2005年提出的一种学习方法,Rahnamayan等[4]用数学推导证明了反向学习的有效性;XU Qing-zheng等[5]探讨了反向学习表现良好背后的原因;Sedigheh Mahdavia等[6]对反向学习近年的发展及发表的文献进行了综述.目前反向学习模型已经应用于各种优化算法,如蛙跳算法[7]、蝗虫优化算法[8]、正弦余弦算法[9]、蝴蝶优化算法[10]等.Wang等[11]首次将反向学习应用于粒子群算法,提出了一种基于OBL的粒子群算法OPSO,随后又提出一般化反向学习(Generalized OBL,GOBL)概念,并增加柯西变异算子一起对OPSO进行了优化形成了GOPSO算法[12].反向学习的引入,有效地加快了粒子群算法的收敛速度和精度.ZHOU Xin-yu等[13]提出的精英反向学习粒子群优化算法(EOPSO),该算法仅对精英粒子,即全局最优粒子和个体最优粒子进行反向学习,并对全局最优粒子采用差分演化变异策略,该策略增强了算法的局部开采能力,算法相对GOPSO在收敛速度及精度上均有提升,突现出精英粒子在粒子群算法中起的引领作用.ZHOU Ling-yun等[14]提出邻域重心反向学习的粒子群优化算法(NCOPSO),算法引入了由Rahnamayan等[15]提出的重心反向学习(Centroid Opposition-Based Learning,COBL)策略,并以粒子的邻域重心为反向点来生成反向解,同时加入了收缩因子拓展COBL的反向搜索空间.该算法充分利用了群体搜索经验,具有更好的收敛精度.

受HPSO算法启发,发现仅仅对最优粒子进行变异就能取得较好的效果,基于此,本文提出了一种对最优粒子进行逐维重心反向学习的变异策略,逐维变异能降低维间干扰[16],重心反向学习能扩大搜索空间、增加种群的多样性、提升收敛精度.且该变异方式可以和各种优化算法结合,都能取得更好的效果.

2 粒子群算法与反向学习

2.1 粒子群算法

PSO算法[1]是模拟鸟类觅食过程提出的一种仿生优化算法,其基本思想是,将解决问题的过程抽象为:在一个空间中,存在很多飞行的鸟,它们有自己的位置以及速度,通过自身的飞行经验和种群相互交流的社会经验,他们不断向有食物的方向飞行.而这个空间就是问题的解空间,鸟就是空间中的粒子,设问题的维数为D,粒子个数为n,全局最优为Gbest=(Gbest1,Gbest2,…,GbestD),第i个粒子xi=(xi1,xi2,…,xiD)的个体最优为Pbesti=(Pbesti1,Pbesti2,…,PbestiD)其第j维速度为vij,位置为xij,更新公式如式(1):

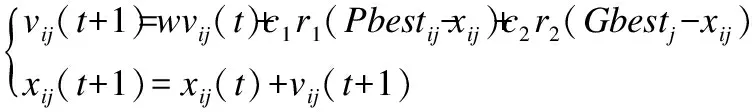
(1)

其中t表示更新代数;i=1,2,…,n表示粒子编号;j=1,2,…,D表示维数;w为惯性权重,且w∈[0,1];c1为个体学习因子,c2为社会学习因子,且c1,c2∈[0,2];r1,r2为区间[0,1]上均匀分布的随机数.

分析该式可知速度更新分三部分,其一为自身先前速度的一部分,受惯性权重w影响,其二为自身飞行经验部分,是向自身Pbesti方向学习的分量,受个体学习因子c1影响,其三为社会认知部分,是向Gbest方向学习的分量,受社会学习因子c2影响.

2.2 反向学习

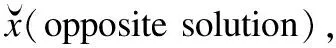
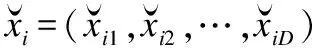
(2)

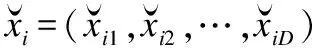
(3)

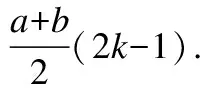
定义3.重心[15](Centroid)：设(x1,x2,…,xn)是D维搜索空间上的带有单位质量的n个点,则整体的重心定义为

(4)

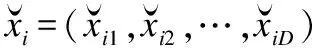
(5)

其中k为区间[0,1]上均匀分布的随机数,其反向过程中中心点的位置是动态的并与重心M相关.

3 逐维重心反向变异粒子群优化算法

3.1 逐维重心反向变异策略

目前的对最优粒子的变异策略大多选取的所有维度或者随机挑取部分维度进行变异,对于高维复杂函数来说,计算其适应度时会因各维相互间的干扰,造成某些维度虽然变得更优但是被另外变得较差的维度所掩盖,变异效率低下,相较于多次的变异,逐维变异的效率更高,通过避免维间干扰,得到的变异解通常更好.

(6)

其中k为区间[0,1]上均匀分布的随机数,Mi为重心M在第i维的分量.

算法1.逐维重心反向变异策略

1.据式(4)计算种群重心M;

2.fori=1 toD

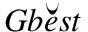
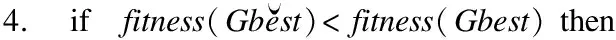
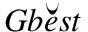
6. end if

7.end for

图1在2维空间上模拟了对Gbest(x,y)反向学习与逐维反向学习的4种可能存在的情况.

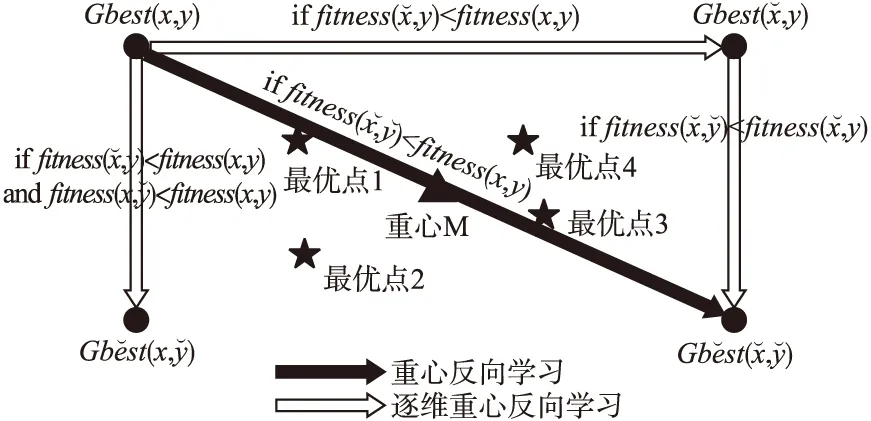
图1 2维空间不同学习策略对比Fig.1 Comparison of different learning strategies in two-dimensional space

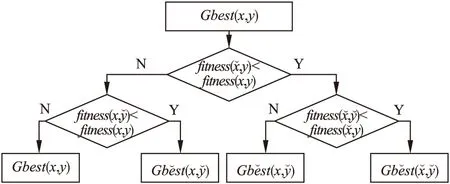
图2 2维粒子逐维重心反向学习流程图Fig.2 Two-dimensional particle Dimensional-by-dimensional centroid opposition-based learning flow chart

表1 2维空间不同学习策略结果对比Table 1 Comparison of different learning strategies in two-dimensional space

分析表1可知逐维重心反向学习比重心反向学习评价的位置更多,所以获得更优解的机会更大,且质量更好,但是反向学习本身的计算开销就很大,所以仅适合单独对最优粒子进行逐维变异,基于这个思想,下面提出一种基于最优粒子逐维重心反向变异策略的粒子群优化算法.

3.2 算法流程

基于逐维重心反向变异粒子群优化算法(DCOPSO)算法流程如下:

Step 1.按照均匀分布随机初始化N个D维的粒子形成初始种群Pop;

Step 2.计算当前种群Pop中每个粒子的适应度fitness来确定个体最优Pbest和全体最优Gbest;

Step 3.根据式(1)更新种群Pop中每个粒子的速度vij及位置xij;

Step 4.计算当前种群Pop中每个粒子的适应度fitness,并更新Pbest以及Gbest;

Step 5.按照算法1进行逐维重心反向变异来更新Gbest;

Step 6.判断当前最优解是否满足终止条件或者达到最大迭代次数,如果是则终止算法,如果不是则返回Step 3.

4 仿真实验与结果分析

4.1 参数设置与测试函数

本文使用Matlab2018a进行仿真实验,选取了表2中的9个经典测试函数,每个函数的最优解均为0.将DCOPSO算法与基本PSO算法、自适应柯西变异的HPSO算法、无变异的COPSO算法进行了对比,参数设置如下:计算次数Time=100次,每次的最大迭代次数Maxgen=1000,种群规模N=30;维数D=30,惯性权重w为[0.4,0.9]之间线性递减,学习因子c1,c2都为2;HPSO中对最优粒子的变异次数M=30;COPSO算法中的反向学习概率P=0.3.

选取的测试函数中,f1-f4为四个单峰函数,f5-f7为3个多峰函数,f8为带旋转和位移的单峰函数,f9为带旋转和位移的多峰函数.

主要有2个测试目的:1)对比逐维重心反向变异与柯西变异的效率;2)分别以不同的方式引入COBL得到的结果如何.

表2 测试函数
Table 2 Test function

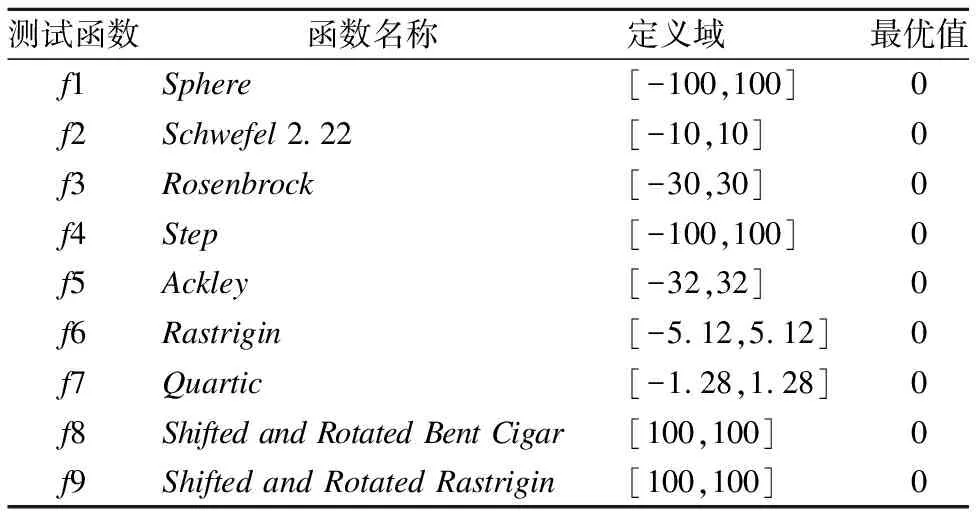
测试函数函数名称定义域最优值f1Sphere[-100,100]0f2Schwefel 2.22[-10,10]0f3Rosenbrock[-30,30]0f4Step[-100,100]0f5Ackley[-32,32]0f6Rastrigin[-5.12,5.12]0f7 Quartic[-1.28,1.28]0f8Shifted and Rotated Bent Cigar[100,100]0f9Shifted and Rotated Rastrigin[100,100]0

4.2 实验结果分析

分析表3实验结果以及图3(a)～图3(i)收敛曲线可知,对于简单的单峰测试函数f1和f2,DCOPSO比HPSO和COPSO的收敛速度及精度均高出很多,这得益于DCOPSO中最优粒子前期快速变异至一个比较好的位置,让种群迅速朝着更优的地方飞行,后期通过逐维的方式避免维间干扰,接受有利变异的维度,使收敛的精度更高.对于较为复杂,难以寻优的病态单峰测试函数f3,HPSO和COPSO很难取得较好的值,而DCOPSO却有小概率寻找到较好的解,且其平均寻优能力也高出不少.在阶梯状的单峰测试函数f4,该函数存在很多平台,DCOPSO的收敛精度比COPSO较好,但是在计算过程中容易遇到所有的粒子处于同一个平台后便出现停滞状态的问题,而HPSO可以借助柯西变异跳出平台继续寻优取得较优的值.在几个多峰测试函数中,HPSO跳出局部最优的几率较低,平均的收敛精度也比COPSO和DCOPSO差,这意味着柯西变异在后期的全局搜索能力变差,很难跳出局部最优解.对于f5和f6,COPSO和DCOPSO均可能收敛到一个比较好的解,但是DCOPSO的收敛精度和稳定性更高,而在f7中情况又相反,这表明DCOPSO在前期的全局搜索能力不如COPSO,但是后期的局部搜索能力更强.在带旋转和位移的函数f8和f9中,DCOPSO明显优于其余算法,表明其具有较好的鲁棒性.

表3 实验结果
Table 3 Experimental results

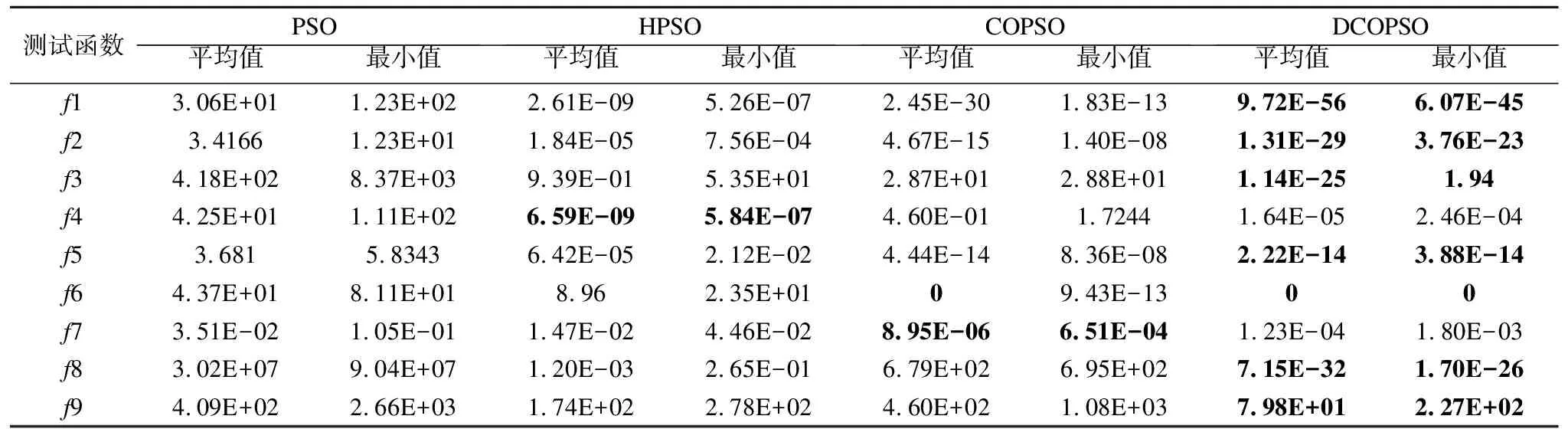
测试函数PSOHPSOCOPSODCOPSO最小值平均值最小值平均值最小值平均值最小值平均值f13.06E+011.23E+022.61E-095.26E-072.45E-301.83E-139.72E-566.07E-45f23.41661.23E+011.84E-057.56E-044.67E-151.40E-081.31E-293.76E-23f34.18E+028.37E+039.39E-015.35E+012.87E+012.88E+011.14E-251.94f44.25E+011.11E+026.59E-095.84E-074.60E-011.72441.64E-052.46E-04f53.6815.83436.42E-052.12E-024.44E-148.36E-082.22E-143.88E-14f64.37E+018.11E+018.962.35E+0109.43E-1300f73.51E-021.05E-011.47E-024.46E-028.95E-066.51E-041.23E-041.80E-03f83.02E+079.04E+071.20E-032.65E-016.79E+026.95E+027.15E-321.70E-26f94.09E+022.66E+031.74E+022.78E+024.60E+021.08E+037.98E+012.27E+02

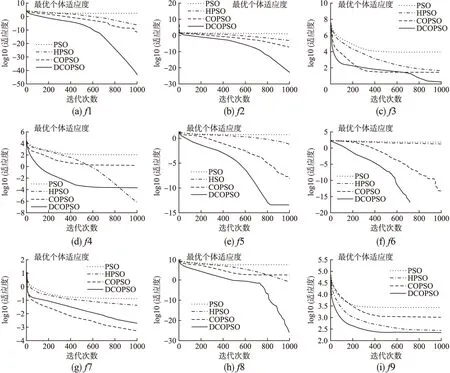
图3 各函数的收敛曲线Fig.3 Convergence curve of each function

表4 平均每次迭代变异次数Table 4 Average number of mutation per iteration

表4记录了HPSO和DCOPSO在9个函数中平均每次迭代变异次数,该数据是变异性能的一个指标,可以从侧面体现变异效率的优劣,分析表中数据可知,DCOPSO的变异频率明显高于HPSO,从测试结果也验证了DCOPSO的变异效果更好.

COBL的引入让PSO算法获得了较大的提升,通过对比一般地使用COBL,逐维地对最优粒子进行COBL取得的效果也很突出.

5 结 语

本文提出了一种逐维重心反向变异的粒子群优化算法DCOPSO,基于逐维变异的思想,采用重心反向学习模型,使全局最优粒子在前期带领种群探索了更大的空间范围,增加了种群的多样性,后期充分利用种群信息找到了精度更高的解.通过理论分析及实验证明,逐维重心反向变异策略优于柯西变异策略.且相较一般的重心反向学习算法,其可以和各类优化算法相结合,均能对算法的全局搜索能力、算法的精度有所提升.