基于长短时记忆神经网络的鄱阳湖水位预测*

郭 燕,赖锡军

(1:中国科学院南京地理与湖泊研究所，中国科学院流域地理学重点实验室, 南京 210008) (2:中国科学院大学资源与环境学院，北京 100049)

鄱阳湖是中国第一大淡水湖，水量主要来自流域“五河”. 汛期，长江水可能倒灌鄱阳湖. 鄱阳湖是典型的季节性吞吐型湖泊，水位年内年际变化剧烈，具有“洪水一片，枯水一线”的特征. 每年4-6月为鄱阳湖主汛期，湖水位随“五河”来水的增加而升高；7-9月是长江主汛期，受到长江高水位的顶托作用，湖水位进一步升高；每年10月-次年3月鄱阳湖属于枯水期，水位较低. 水位变化会导致湿地植被分布以及候鸟栖息等也相应发生改变[1-3]. 近十几年来，在气候变化和高强度的人类活动影响下，鄱阳湖水情发生了剧烈的变化，特别是枯水问题突出，出现了枯水发生时间提前、持续时间延长的现象. 湖区生态环境因水量平衡的变化面临威胁[4-5].

鄱阳湖水量平衡近年成为了学界关注热点. 为阐明鄱阳湖的水量变化，开展了大量卓有成效的研究，建立了诸多水文水动力模型和数理统计模型，分析了气候变化和不同类型的人类活动对鄱阳湖水量的影响过程以及江湖交互作用下湖泊水位的变化特征[6-9]. 水动力模型可实现过程的精细模拟，但是水动力系统庞大、需要非常完善的基础资料、计算复杂、耗时较长，对水位高效预测仍存挑战[10-11]. 数理统计方法(如：多元线性回归(MLR)、累积距平曲线(CPC)、概率分布函数(PDF)、泰尔森方法(TSA))简单易行，主要用于长时间尺度的变化检验分析[12-16]. 鄱阳湖水位受流域“五河”和长江来水多重控制，其变化与“五河”来水和长江来水有着非常复杂的非线性关系[17]，难以采用简单的统计模型模拟预测水位和来水的响应关系. 人工神经网络方法作为一种数据驱动的自适应性方法，没有先验假设，可较好地模拟预测复杂的非线性作用关系，也在鄱阳湖得到了应用[18]. 近年来，基于人工神经网络的深度学习算法得到了飞速发展. 特别是长短时记忆神经网络方法(long short-term memory,LSTM)，它通过循环反馈结构存储历史信息，具有较强的时间序列问题求解能力，在模拟预测水文时间序列问题中受到关注. Zhang等[19]基于雨量器和水位传感器的在线数据，比较了不同神经网络结构在模拟和预测挪威Drammen联合下水道结构水位方面的性能，证实了LSTM比没有显式细胞记忆的传统架构更适合于多步预测. Zhang等[20]使用LSTM预测农业地区的地下水位，并将基于LSTM方法的预测结果与传统神经网络的预测结果进行了比较，发现前者的性能优于后者. Lee等[21]利用基于物理的水文模型SWAT和数据驱动的深度学习算法LSTM，在湄公河下游Kratie站进行了径流模拟. Liu等[22]提出了改进的CA-LSTM上下文感知神经网络，基于收集到的洪水因子序列数据对洪水进行了预测.

鄱阳湖水位受江湖共同制约，其变化与流域“五河”来水量及长江来水量具有非常复杂的非线性关系. 本文选取鄱阳湖为研究对象，采用LSTM神经网络方法，建立鄱阳湖水位日尺度的预测模型，探讨其用于预测江湖交互作用下鄱阳湖水位变化过程的潜力，为鄱阳湖水量平衡研究提供一个快速有效的预测方法.

1 数据和方法

1.1 研究区概况

鄱阳湖(28°24′～29°46′N，115°49′～116°46′E)位于长江中下游南岸，北部较平坦，东西南三面环山，全流域总体地势是南高北低，南部地形起伏变化较大，形成了一个以鄱阳湖为底，向北开口连接长江的巨大盆地. 鄱阳湖流域由赣江、抚河、信江、饶河和修水5个相互独立的子流域组成，与湖区共同形成了一个完整的流域系统，流域总面积为16.2×104km2[16, 23]. 多年平均径流量为1491亿m3，水位年内变幅为9.59～15.36 m.

1.2 研究数据

选用“五河”流域外洲站、李家渡站、梅港站、渡峰坑站、虎山站、万家埠站和长江中游汉口站7站逐日平均流量数据以及湖口站、星子站、都昌站、吴城站和康山站5站逐日平均水位数据建模，时间序列长度均为1956-2000年,监测站点分布见图1.

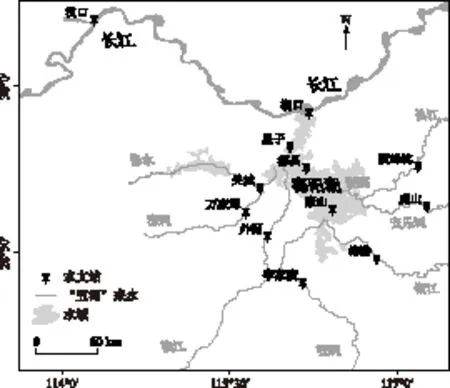
图1 鄱阳湖监测站点的空间分布Fig.1 Location of sampling sites in the Lake Poyang

1.3 LSTM基本原理

1.3.1 LSTM前向计算 LSTM是1997年Hochreiter和Schmidhuber[24]为了解决RNN模型的梯度消失或爆炸缺陷而开发的一种复杂的递归模型. Gers等[25]正式提出LSTM网络层是由遗忘门f、输入门i、记忆单元C和输出门o组成(图2). LSTM的关键是记忆单元，它像传送带一样，将信息从上一个单元传递到下一个单元.

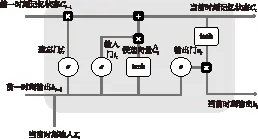
图2 LSTM内部结构示意图Fig.2 Schematic diagram of the internal structure of LSTM

首先，决定从记忆单元中增减多少信息. 遗忘门本质上是一个σ神经网络层，根据前一时刻的输出ht-1和当前的输入Xt，产生一个介于0和1之间的ft值：

ft=σ(Wxf·Xt+Whf·ht-1+bf)

(1)

接下来，确定将在记忆单元中存储哪些新信息. 这一部分由一个σ神经网络层和一个tanh神经网络层两部分组成. 输入门根据前一时刻的输出ht-1和当前的输入Xt，产生一个介于0和1之间的it值：

it=σ(Wxi·Xt+Whi·ht-1+bi)

(2)

(3)

从而更新记忆单元：

(4)

最后，我们决定输出什么信息. 首先，运行一个σ神经网络层来决定输出记忆单元的哪些部分. 然后，通过tanh神经网络层将Ct值调整为-1～1，并将其乘以σ神经网络层的输出，最终得到目标信息.

ot=σ(Wxo·Xt+Who·ht-1+bo)

(5)

ht=ot·tanh(Ct)

(6)

式(1～6)中，f、i、o、C和h分别是遗忘门、输入门、输出门、记忆单元和输出信息，W是相应的权重矩阵，b是偏差矩阵，σ和tanh是激活函数.

1.3.2 LSTM反向训练 神经网络训练的过程是去寻找最优参数，使得模型收敛，即损失函数达到极小甚至最小的过程. 网络通过反向传播损失函数，利用梯度下降法迭代更新网络的权重[26-27]. 我们选取最常用的均方误差计算损失函数：

(7)

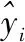
1.4 模型评估标准

LSTM是通过已有的训练样本(即已知数据及对应的输出)去学习得到一个最优模型，再利用该模型将所有的输入映射为相应的输出. 我们采用均方根误差(RMSE)、纳什效率系数(NSE)和决定系数(R2)3个指标对模型模拟的效果进行评价[28].

(8)

RMSE值为0表示观测值与预测值完全吻合.

(9)

NSE是一个参数，它决定了剩余方差(噪声)相对于测量数据(信息)中的方差的相对重要性，取值范围为负无穷至1. 接近1，表示模拟效果好，模型可信度高；接近0，表示模拟结果接近观测值的平均值水平，即总体结果可信，但过程模拟误差大.

(10)

2 鄱阳湖水位预报模型构建

2.1 模型结构

采用单层LSTM循环神经网络建模，输入长江和“五河”来水量，其中长江水量以汉口站流量为代表，“五河”水量以赣江外洲站、抚河李家渡站、信江梅港站、饶河渡峰坑站和虎山站、修水万家埠站流量为代表，输出湖口站、星子站、都昌站、吴城站和康山站5个代表站的水位，实现根据“五河”来水量和长江来水量组合预测鄱阳湖湖区未来1 d水位的空间分布，神经网络结构见图3，表达式为：

(11)

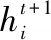
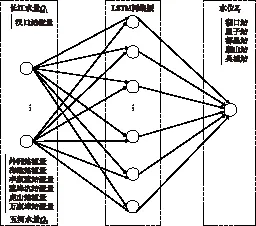
图3 单层长短时记忆网络LSTM模型结构Fig.3 Structure of a single layer LSTM model

数据之间的差异性会对模型的学习能力产生负面影响. 因此，为了保证构建的模型中参数能够稳定收敛，在神经网络训练之前需对其进行预处理，以确保所有变量保持在相同的量表上[29-30]. 我们对所有数据进行[0,1]归一化处理：

(12)

式中，X是归一化后的数据，Xori是原始数据，Xmax和Xmin分别是原始数据的最大值和最小值.

模型损失函数选用均方根误差，优化选取基于梯度下降的ADAM算法，采用Dropout正则化方法防止模型过拟合[31-33]. 训练集为1956-1980年的水文时间序列数据，验证集数据长度为1981-2000年. 在LSTM神经网络中，输入时间窗、隐藏神经元数目、初始学习率大小等重要参数会直接影响到模型预测效果. 所以，接下来我们将对模型中的这些参数进行优选.

2.2 模型参数优选

2.2.1 输入时间窗长短对模型模拟效果的影响 鄱阳湖作为大型通江洪泛湖泊，其入湖流量与湖泊水位关系呈现明显的非线性特征，加之长江与湖泊之间相互作用的复杂性，湖泊流量与水位之间呈现多种对应关系[34]. “五河”水量经一段时间传输入湖，鄱阳湖接受“五河”及长江来水进行调蓄作用，因而水位和流量并不总是同步变化，存在明显的相位滞后效应，输入时间窗的优选计算就是确定流量-水位之间滞后时长的过程. 我们计算并比较了不同长短的输入时间窗(1～10 d，即分别将当前时刻的流量、前2 d内的流量、……、前10 d内的流量作为输入变量)下，根据“五河”来和长江来水量，组合预测鄱阳湖湖区未来1 d的水位空间分布. 同时，为了确保模型较高的准确率，隐藏神经元数目应尽量多取，设置了100个；初始学习率大小应定义为较小的值，设置为0.001. 不同输入时间窗模式下模型拟合评价指标计算结果如图4所示.

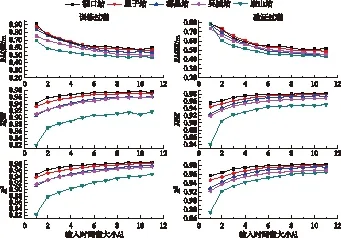
图4 不同输入时间窗下模型训练和验证过程的模拟结果Fig.4 Simulation results of model training and verification under different input time windows

虽然神经网络模型的外延效果一般不是很理想，但可通过反复对模型调试计算、选取最适宜的输入时间窗来提高模型预测效果. 图4结果表明：不同输入时间窗下，湖口站水位预测的效果均最好，其次分别是星子站、都昌站和吴城站，康山站水位预测效果为五站中最差. 利用当前时刻的七站流量来预测未来1 d的鄱阳湖五站水位时，湖口站训练和验证过程的RMSE均较大，分别为0.91 m和0.79 m.NSE和R2相对较小，训练阶段NSE为0.94，R2为0.95；验证阶段NSE和R2均为0.96. 随着输入时间窗逐步延长，模型训练和验证阶段的模拟效果都稳步提高. 当输入时间窗为7 d时，模型各项性能指标已达到很好的效果，继续增大输入时间窗，模型预测效果没有明显提高. 因此，我们选择利用“五河”六站及长江干流汉口站这七站前7 d内的流量来预测鄱阳湖湖口、星子、都昌、吴城和康山站未来1 d的水位. 其中，湖口站训练和验证阶段的RMSE分别为0.62和0.55 m，NSE分别为0.97和0.98，R2均为0.98.

2.2.2 隐藏神经元数目对模型模拟效果的影响 LSTM网络层中隐藏神经元数目是影响模型预测结果准确率的重要参数之一. 若数量太少，网络不能很好地学习，需要训练的次数也多，训练精度也不高；若数量太多，训练时间又较长，甚至可能导致模型不收敛[35-36]. 因此，我们进一步计算了隐藏神经元数分别为1、5、10、20、30、40、50、100、200、500共10种模式下，根据前7 d“五河”六站及汉口站流量组合预测鄱阳湖5站未来 1 d 的水位空间分布，相应的训练和验证阶段模型拟合评价指标的计算结果如图5所示.

图5 隐藏神经元数目对模型训练和验证过程的模拟结果的影响Fig.5 The effect of the number of hidden nodes on the simulation results of model training and verification

计算结果表明，一定范围内随着隐藏神经元数目的增加，模型在训练和验证阶段的水位预测效果均稳步提高，但当隐藏神经元数目增加到一定值之后，继续增加其数量模型预测效果变化不大. 隐藏神经元数为1个时，各站水位预测效果最差. 湖口站水位训练和验证阶段的RMSE均高达1.0 m以上，分别为1.02 和1.13 m，NSE和R2均相对较低. 隐藏神经元数目为50个时，各站水位预测效果的评估指标均达到平稳. 其中，作为5个水位站中预测效果最差的康山站，RMSE仅为0.45 m，NSE为0.95，R2为0.96. 考虑到模型预测精度以及计算时间，我们设置了50个隐藏神经元节点. 模型训练阶段的RMSE为0.61 m，NSE为0.97，R2为0.98；验证阶段的RMSE为0.53 m，NSE为0.98，R2也为0.98.

2.2.3 初始学习率大小对模型模拟效果的影响 学习率表示每次迭代后权重的更新量，学习率太小，模型更新速度慢；学习率过大，模型可能错过最优解. 为了找到模型的全局最优解，我们借助基于梯度下降的具有相当鲁棒性的ADAM自适应学习率优化算法作为优化器[37]，算法描述为：

mt=β1·mt-1+(1-β1)gt

(13)

(14)

(15)

(16)

(17)

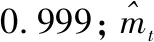
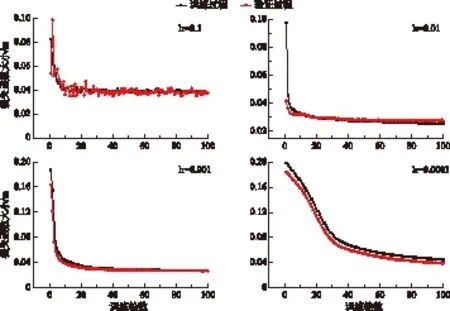
图6 初始学习率大小对模型训练和验证过程的模拟结果的影响Fig.6 The effect of the initial learning rate on the simulation results of model training and verification

计算了4种初始学习率(分别为0.1、0.01、0.001和0.0001)下模型训练和验证阶段损失函数的大小(图6). 我们发现，初始学习率为0.1时，损失函数曲线随着迭代次数的增加发生不同幅度的震荡，此时学习率选择过大；当初始学习率为0.01时，训练阶段的损失函数具有较好的学习过程，但验证阶段的损失函数曲线迅速下降，模型学得太快，基于对模型精度和速度的综合考虑，认为初始学习率过大；当初始学习率为 0.0001 时，则经过较长时间模型才得以收敛. 因此，我们选取训练和验证阶段均有很好的学习过程曲线的 0.001 作为最适初始学习率，且模型快速地收敛于0.03. 此时，五站中水位预测效果最好的湖口站，训练和验证阶段的RMSE分别为0.58和0.50 m，NSE均为0.98，R2也均为0.98. 预测效果相对最差的康山站，验证阶段的RMSE为0.42 m，NSE和R2分别可达0.95和0.96. 康山站的RMSE值反而比湖口站的低，是因为各站年内水位变幅存在差异，康山站多年年内变幅均值为6.03 m，而湖口站可达12.00 m.

3 水位预测

3.1 预测结果分析

综上所述，最终我们建立了含50个隐藏神经元的单层LSTM神经网络，采用基于梯度下降的自适应学习率的ADAM优化算法，初始学习率为0.001，利用“五河”六站和长江干流共7个流量站前7 d内的日均流量，组合预测鄱阳湖从北到南5个水位站未来1 d的日均水位. 将1956-1980年水文序列数据作为训练集，1981-2000年数据对模型进行验证. 构建的LSTM模型对湖口、星子、都昌、康山和吴城站的水位预测精度较高，模型拟合的各项评价指标如表1所示，训练阶段和验证阶段RMSE都很小，范围分别为0.48～0.60 m和0.41～0.50 m. 同时，训练和验证阶段的NSE和R2都很大，几乎接近于1. 其中，训练阶段和验证阶段的NSE范围分别为0.92～0.98和0.96～0.98；两个阶段的R2范围则分别为0.93～0.98和0.96～0.98. 湖口站和星子站1981-2000年水位预测的验证结果如图7所示，以两站2000年的水位过程线为例，湖口站年均水位实测值和预测值分别为12.98和13.26 m. 最高日均水位实测值为18.10 m，预测值较之大0.62 m，但与年均水位相比，相差较小，具有较强的可靠性. 日均最低水位的实测值与预测值分别为7.73和7.61 m，较年均和年最高水位值的预测结果更精确. 构建的LSTM模型对湖泊最下游湖口站的水位预测精度最高，从最上游康山站至湖口站，模型对五站水位预测精度有逐步增强的趋势，这可能和湖区各站受长江的顶托关系逐渐趋弱有关.

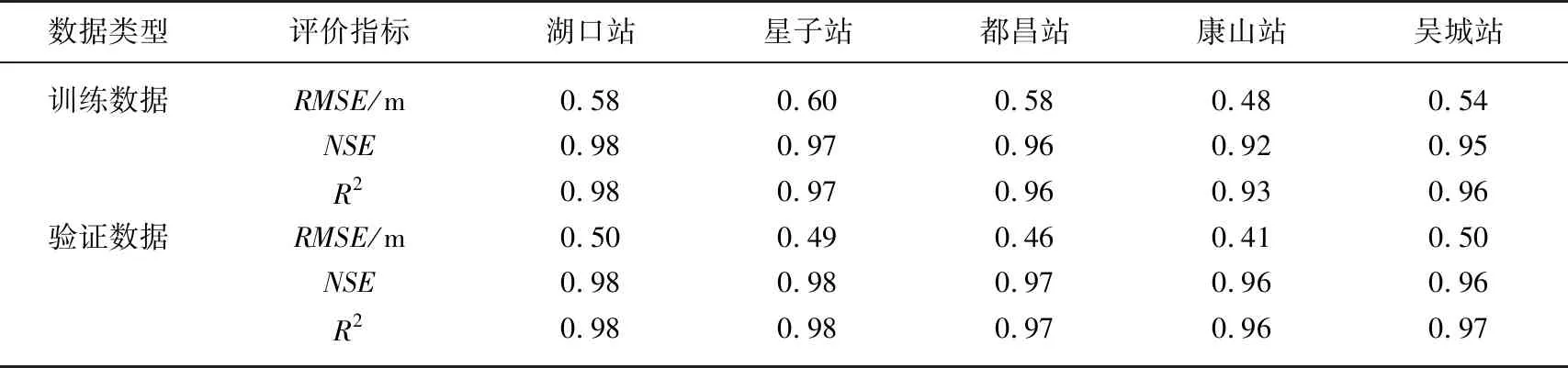
表1 最佳模型评价指标计算结果

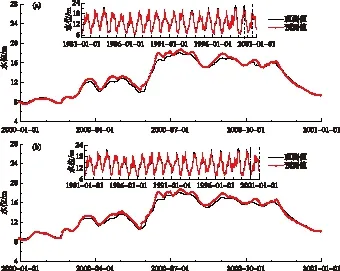
图7 1981-2000年湖口站(a)和星子站(b)水位预测结果Fig.7 Water level prediction results of Hukou station (a) and Xingzi station (b) from 1981 to 2000

3.2 模型能力比较

为了充分验证本文构建的LSTM模型的水位模拟精度，突出模型的优势以及后续模型应用，我们也用一般的循环神经网络BP神经网络对鄱阳湖水位进行模拟，并与LSTM模型的模拟精度进行对比. BP神经网络同样是将1956-1980年水文序列数据作为训练集，1981-2000年数据对模型进行验证，利用“五河”六站和长江干流共7个流量站前7 d内的日均流量，组合预测鄱阳湖从上游到下游5个水位站未来1 d的日均水位. 比较了两种方法的各项评价指标(表2).

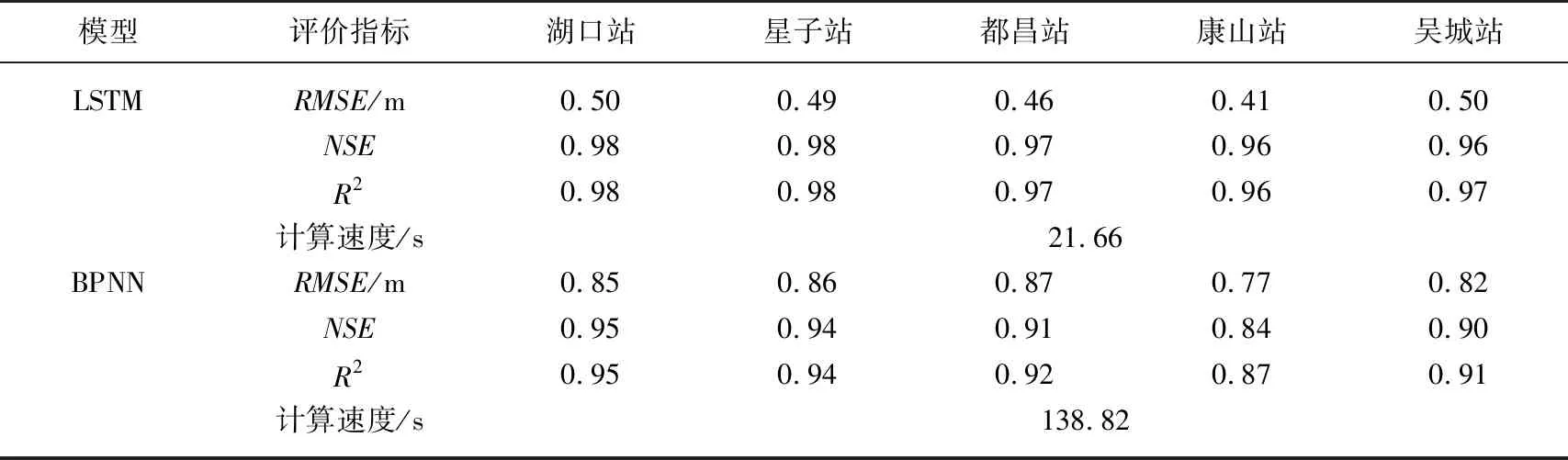
表2 两种神经网络方法验证阶段评价指标计算结果对比

图8 三种训练数据集下模型验证结果比较Fig.8 Comparison of model verification results under three training data sets

对五站水位的预测，LSTM模型得到的最佳RMSE值均低于0.50 m，而BPNN模型得到的最佳RMSE值除最上游康山站为0.77 m，其他四站的RMSE值均高于0.80 m；LSTM模型得到的NSE，预测精度最低的康山站水位也达到0.96，而BPNN得到的NSE，预测精度最高的湖口站水位也仅有0.95. 不难看出，我们构建的LSTM模型模拟精度明显强于BPNN模型. 除了模拟精度外，计算速度也是衡量模型性能的一个重要指标. 计算了两种模型的计算速度，结果表明，LSTM模型的计算速度(21.66 s)明显快于BPNN的计算速度(138.82 s). 综上，构建的LSTM模型在精度和速度上较BPNN模型均具有明显的优势.

3.3 训练数据集的影响

实际情况中，应尽可能选取足够多的数据来建模，但由于各种不可抗因素，往往无法获取完整的水文时间序列数据. 为此，我们需要考虑选用不同的训练数据集，分析模型的效果. 我们基于水文时间序列数据自身的特点，利用上述参数设计好的LSTM模型，设计3种方案分别对五站水位进行预测，分别为：①训练集数据为长时间序列(1956-1980年)；②训练集数据较短时间序列(1956-1960年)；③训练集数据时间序列为5个典型年：1954年、1973年、1974年、1977年和1978年. 根据《水文情报预报规范》(GB/T 22482-2008)中的距平百分率划分径流丰平枯的标准，1954年和1973年是典型的丰水年，1977年是平水年，1974年和1978年为典型的枯水年. 利用1981-2000年的数据进行验证，比较3种训练集数据模式下模型拟合的效果.

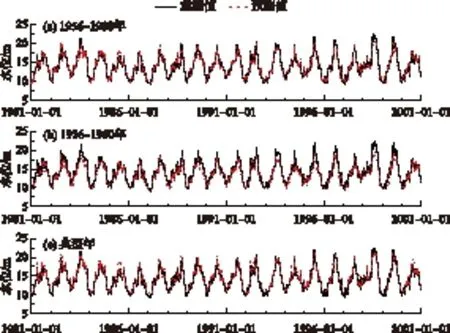
图9 三种训练集训练模式下都昌站1981-2000年水位预测结果Fig.9 Water level prediction results of Duchang station from 1981 to 2000 under three training sets

五站水位预测效果的各项评价指标计算结果如图8所示，同种预测方案中，湖口站水位预测效果均最好，康山站均最差. 方案①中，湖口站验证阶段RMSE、NSE和R2分别为0.51 m、0.98和0.98；康山站相应的指标计算结果分别为0.43 m、0.95和0.95. 方案②中，五站水位预测的效果明显降低. 湖口站RMSE、NSE和R2分别为0.93 m、0.94和0.97；康山站相应的指标计算结果分别为0.88 m、0.80和0.91. 方案①和方案②中训练集的样本量分别为9126和1827. 而将样本量为1820个的5个典型年的数据作为训练数据进行模型训练时，五站水位的预测效果与方案①相比较差，但明显优于方案②的预测效果. 湖口站RMSE、NSE和R2分别为0.76 m、0.96和0.96；康山站相应的指标计算结果分别为0.56 m、0.92和0.93. 所以，我们在利用LSTM神经网络预测湖泊水位时，应尽可能选取足够长时间序列的数据. 若因为不可抗因素无法获取完整的数据序列，选取涵盖各种代表性数据的典型年数据进行训练，也可以获得较好的模型预测效果.

都昌站代表鄱阳湖主湖区水位，3种方案下其水位预测的结果如图9所示(其他水位站预测结果与其相似，故图省略)，当1956-1980年数据作为训练时间序列时，五站多年水位的预测值与真实值之间具有非常高的对应关系. 1956-1960年是鄱阳湖典型的枯水期，因而模型通过训练能够较好地反映低水位特征. 5个典型年涵盖了几个重要的丰、枯水年信息，总体预测效果介于前两者之间.