雷达精度飞行试验目标飞机选择分析*

郑全普，郑光勇，赵文杰，霍烁烁，谢婷婷

(中国洛阳电子装备试验中心，河南 洛阳 471003)

0 引言

在雷达检飞试验中，探测精度是雷达的一项重要战技指标，对雷达的探测精度考核就成为雷达试验中一个极其重要的题目。雷达的探测精度都是对某种典型目标提出来的，如对典型目标或者对某种特定机型的探测距离是多少、探测精度是多少。而在实际的雷达精度试验中，由于条件限制，有时难以找到雷达散射截面积(radar cross section，RCS)为规定值或特定机型的飞机，因此必须用不同RCS、不同机型的飞机进行雷达探测精度的试验，然后通过等效替代的方法推算到对应考核要求的指标上[1]。

通常情况下，探测精度的试验数据往往受到合作目标配试飞机尺寸、形状、RCS的影响。选择不同的机型，试验数据会随着飞机的尺寸、形状、RCS的变化而变化，如果变化的范围超出了试验允许值，会致使试验得到的试验数据不满足统计条件而不可用[2]。本文将对不同配试目标对雷达精度试验数据的影响展开分析，探讨在选择不同机型的飞机时，飞机因素对试验结果的影响，提出配试飞机选择方法。

1 不同目标对精度试验的影响

在雷达精度试验中，主要考核的指标为：方位探测精度，距离探测精度和高度探测精度。在这些指标考核中，目标由于其外形尺寸不同、运动状态不同、RCS不同等，其对试验数据会产生不同的影响。

1.1 方位误差分析

在方位误差中，不同目标对试验数据的影响主要来源于2个方面：动态跟踪误差和随机误差[3-4]。

1.1.1 动态跟踪误差

动态跟踪误差主要是指动态滞后误差。滞后误差指跟踪系统在雷达坐标系统中因为没有能够跟踪上目标的速度、加速度或者更高阶导数而形成的误差。滞后误差可以用目标轨迹的泰勒展开式中的运动参数除以一个跟踪系统的误差常量来表示为

(1)

式中：x为目标位置；Kp为位置误差常量；Kv为速度误差常量；Ka为加速度误差常量。

1.1.2 随机误差

(1) 角闪烁

闪烁误差指雷达跟踪一个复杂目标时的随机跟踪误差分量，它由目标多个不同散射中心反射回来的信号相互干涉而形成闪烁误差。目标角闪烁表现为到达天线的反射波的等相位面发生变化，或者说是目标的等效视在中心产生移动，因而产生角度跟踪误差。移动的大小与目标横向(垂直于雷达射线)尺寸有关，理论和实践都表明有10%～20%的时间甚至会移动出目标横向尺寸之外。

角闪烁误差估计公式为

(2)

式中：Ls为目标横向尺寸(水平方向尺寸)；R为目标到被试装备的斜距。

(2) 动态滞后变化

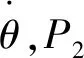
(3)

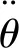
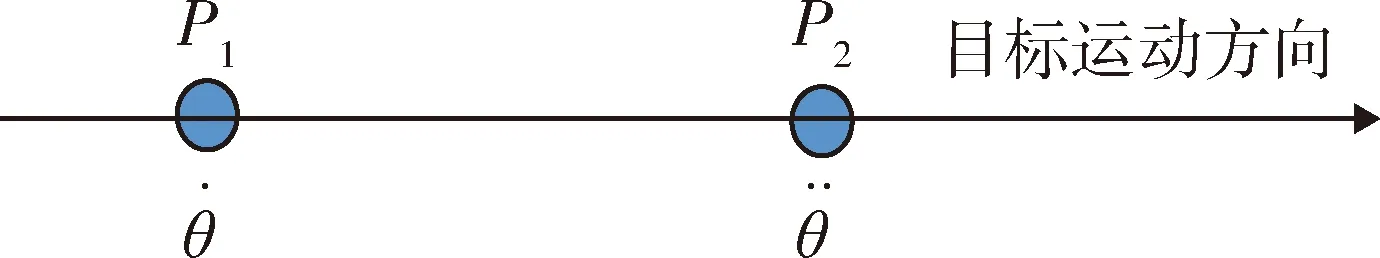
图1 动态滞后变化的产生

再根据加速度误差的变化，可以得出动态滞后变化误差Δεθd为

(4)

(3) 热噪声误差

进入跟踪雷达接收机的热噪声会给角误差检波器输出造成误差，在不同信噪比时误差不同，在低信噪比时极为重要。

圆锥扫描雷达中由接收机热噪声造成的角误差均方根值为

(5)

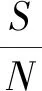
脉冲跟踪系统中由接收机造成的角误差为

(6)

式中：km为角误差检测斜率。

1.2 距离误差分析

在距离误差中，不同目标对试验数据的影响主要来源于2方面：动态跟踪误差和随机误差。

1.2.1 动态跟踪误差

动态跟踪误差主要为动态滞后误差。与角度动态滞后类似，距离动态滞后误差的估算公式为

(7)

在精密跟踪雷达系统中，当径向速度较大时，通常需要进行动态滞后修正。

1.2.2 随机误差

(1) 距离闪烁

由目标引起的距离闪烁跟踪误差与角闪烁噪声误差相似。对飞机而言，典型的距离闪烁均方根误差为目标跨度的0.1～0.3倍，其中由机尾和机头观察时接近0.3倍，由侧面观测时接近0.1倍[5]。

通常在雷达系统精度设计时，距离闪烁均方根误差用公式估算为

σR=(0.2～0.35)Lr，

(8)

式中：Lr为目标在距离向上的尺寸。

(2) 动态滞后误差

距离跟踪动态滞后变化误差的原因和形式类似于角度跟踪系统的动态滞后变化误差。其误差估算公式为

(9)

一般运动情况下，动态滞后变化误差都很小，大部分跟踪雷达中可以不考虑。

(3) 热噪声误差

距离跟踪测量的噪声误差大小与雷达信号的有效带宽和有效信号噪声比有关。在不同探测目标RCS不同，会带来不同的信噪比，由不同的信噪比带来的随机误差为

(10)

式中：τR为被试设备的脉冲宽度；Kr为常数，一般取值1.4～2.0；β为距离跟踪回波有效带宽。

1.3 高度误差分析

根据测得的目标斜距和仰角，并考虑到地球曲率和大气折射的影响，可按图2所示的几何关系计算目标高度[6-8]。ae=8 490 km为考虑大气折射后的地球等效半径，ha为雷达天线高度，ht为飞机的高度。

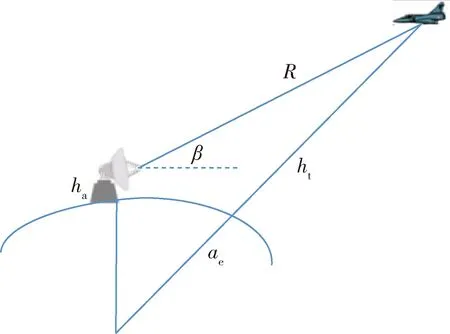
图2 目标高度的计算

由余弦定理可近似得到

(11)

若目标距离较近，雷达天线不高，式(11)可以简化为

ht≈Rsinβ.

(12)

由式(12)可以得到

dht=sinβdR+Rcosβdβ.

(13)

2 雷达精度试验配试飞机选择

在精度试验中，配试飞机通常作径向、等高、匀速的往返水平飞行[9-12]，试验布局及飞行航线可由图3表示。

在精度试验中，飞机沿着径向直线飞行时，运动状态的变化率很小，因此动态跟踪误差、动态滞后误差变化很小，通常可以忽略；而当飞机在进行转弯机动时，动态跟踪误差、动态滞后误差变化很大，有时还会影响到雷达的跟踪，因此在精度试验数据处理中，通常不能使用这段数据。所以在精度试验中，不同配试飞机对试验数据的影响主要表现在闪烁误差和热噪声误差。

在实际雷达精度试验中，通常用典型飞机作为配试飞机[13-14]；但在某些情况下，由于条件限制，必须用其他飞机代替。下面以对空情报雷达精度试验为例，分别分析苏-27与歼-7飞机作为配试飞机对精度的影响。苏-27与歼-7飞机对试验结果的影响表现在2种飞机的外形尺寸不同而带来验数据误差，以及由于2种飞机RCS不同而带来的信噪比不同引起的热噪声误差。在探测精度试验中，通常要求真值的精度高于测量值精度的3倍[8]，因此在采用不同配试目标时，目标对测量误差的影响远小于测量指标的1/3，则可以认为配试目标对试验结果没有影响。文献[14-16]给出了歼-7飞机和苏-27飞机的典型参数，见表1所示。

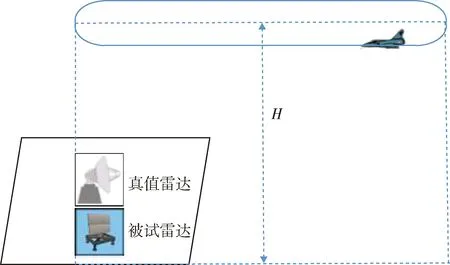
图3 精度试验飞行航线示意图

表1 歼-7飞机和苏-27飞机的外形尺寸表

2.1 方位精度分析

通过前面的分析，在精度试验中不同配试飞机对试验数据的影响要考虑的是角闪烁、热噪声误差带来的误差。

2.1.1 角闪烁

配试设备在最近端时，可以计算出歼-7飞机、苏-27飞机引起的最大方位向误差为

(14)

2.1.2 热噪声误差

信噪比公式为

(15)

式中：P为雷达功率；G为天线增益；λ为工作波长；Ls为综合损耗；Bn为接收机工作带宽。

在配试飞机飞到最远端300 km时，S/N最小，随机误差最大，得到歼-7飞机和苏-27飞机所带来的角度最大随机误差分布为0.015°和0.007°。

从上面可以计算出由配试飞机所带来的方位累计误差为：歼-7飞机为0.022°,苏-27飞机为0.021°，相对于雷达的探测精度小了2个数量级，因此在试验中可以不考虑由于配试飞机不同而给方位精度试验数据带来的影响。

2.2 距离精度分析

同方位精度一样，在精度试验中不同配试飞机对雷达探测精度试验数据的影响主要需要考虑的是距离闪烁、热噪声误差带来的误差。

2.2.1 距离闪烁

由于歼-7飞机、苏-27飞机在进行精度飞行时是作径向飞行，飞机在距离向上的尺寸即为飞机的长度，飞机的最大距离闪烁误差为

歼-7：σR=0.35×13.95=4.9 m,苏-27：σR=0.35×21.93=7.6 m.

(16)

2.2.2 热噪声误差

根据热噪声误差公式，可以计算出歼-7飞机和苏-27飞机所带来的距离最大随机误差分别为2.3 m和1.2 m。

从上面可以计算出由配试飞机所带来的距离累计误差为：歼-7飞机为7.2 m、苏-27飞机为8.8 m，相对于雷达的探测精度小了2个数量级，因此在试验中可以不考虑由于配试飞机不同而给试验数据带来的影响。

从分析中可以看出，歼-7飞机、苏-27飞机所带来的距离精度误差接近10 m，因此在探测精度为米级的雷达精度试验中，最好用尺寸更小的飞机作为配试目标。

2.3 高度精度分析

由于目标不同而对试验数据带来的影响可以由式(13)计算。通过前面的分析，歼-7飞机、苏-27飞机所带来的距离误差远小于指标要求，简化起见取指标100 m。

由式(13)所知，当飞机在最远端时所带来的数据影响最大，为方便计算，飞行距离取300 km，高度取8 000 m，得到俯仰角度β为1.5；设探测波束为笔形波束，方位波束宽度与俯仰波束宽度相同，可以计算出热噪声误差带来的俯仰测角误差，带入式(13)计算得到：

歼-7：dht=sinβdR+Rcosβdβ≈80.8 m,苏-27：dht=sinβdR+Rcosβdβ≈42.4 m.

(17)

从计算结果可以看出，歼-7飞机、苏-27飞机所带来的测量误差远小于指标要求，因此在试验中可以不考虑由于配试飞机不同而给试验带来的影响。

3 结束语

通过本文分析可以看出，由于歼-7飞机尺寸和RCS都比苏-27飞机小，其对雷达探测精度试验数据的影响比苏-27飞机小。因此在条件允许的情况下，歼-7飞机是进行精度飞行试验的首选飞机。在难以找到歼-7飞机作为配试飞机时，选用其他配试机型，需要按照第1节的公式计算配试飞机所带来的测量误差，只有配试飞机所带来的综合误差小于雷达的探测精度指标要求的1/3时，才可使用此机型进行探测精度飞行试验。在本文分析中，苏-27飞机对探测精度试验数据的影响虽然比歼-7飞机大，但是由其带来的误差远小于指标要求的1/3，因此可以用其进行试验。