运输车辆安全驾驶行为分析

王畅 蒋思琦 韩依洋

摘 要：针对第七届“泰迪杯”数据分析职业技能大赛C题——运输车辆安全驾驶行为分析，以欧氏距离和物理方法为基础，建立基于轨迹与速度特征异常检测模型，基于差分与最小二乘法轨迹拟合模型，综合运用MATLAB软件编程求解，得到良好的数据拟合路线图等结论。

关键词：欧氏距离;差分;最小二乘法;MATLAB

0 引言

随着信息技术的发展，以及车载运行监控系统的不断改进，为了充分利用交通运输企业的车联网数据，挖掘车辆驾驶行为的潜在特征，对监控系统所统计的数据进行合理的整理，可以为数据的进一步挖掘提供良好的保障。

1 模型假设

（1）假设车辆行驶是在二维的平面上，即不考虑地球的形状及地面的高度差。

（2）假设每辆车仅有一名驾驶人员。

2 基于轨迹和速度特征异常检测模型

2.1 模型建立思想

由于原有数据的数据量大且存在异常轨迹的情况，即需要通过有效的方法解决异常轨迹并且得到拟合数据。针对异常轨迹的检测，R-Tree异常轨迹检测算法是目前常用的异常轨迹检测方法。R-Tree异常轨迹检测算法是通过找出每个轨迹点的w-邻域点集，与该轨迹点构成点对集合，每个轨迹点仅和其w-邻域点集中的点进行比较，然后通过指定的邻域阈值w找出异常轨迹，但是此方法对于长且复杂的轨迹，表现出异常轨迹分段平均化的现象。即在此基础上我们提出了根据相邻两点数字特征综合考虑数据的异常情况。

2.2 模型建立

對于轨迹特征，通过欧几里的距离进行两点之间的距离计算，设定两个坐标点在二维空间上的距离则两点之间的轨迹弯曲程度本文使用两点之间的移动距离与两点之间的形成的直线距离的比值衡量。

对于速度特征，数据的位置变化代表着车辆运动时位置随时间的变化情况。对于等时变化的数据，可以得到速度vi与位移li的关系：则相应的加速度：

综合考虑轨迹特征和速度特征，设定相应的阈值，对数据进行异常点的处理。

2.3 基于差分与最小二乘法轨迹拟合模型

由于车辆的行驶轨迹没有规律性，即在不同区域内，形成的轨迹可以完全不同，所以不能通过高次拟合的方法来完整的拟合车辆的行驶轨迹;离散的数据对应不同的坐标和不同的方位角，因此拟合过程中的拟合曲线是否连续或者拟合结果是否能够组成一条连续的轨迹并不是必需的。故根据差分和最小二乘法的思想来分段的拟和轨迹，并且获取合适的方位角。

2.4 结果分析

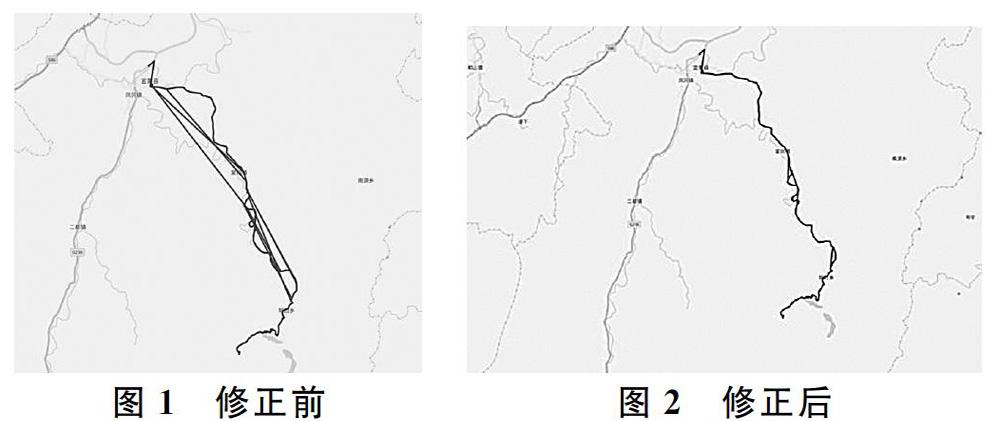
通过MATLAB软件编程可以得到，以其中两条路线为例（如图 1、图 2所示）。

根据数据处理和轨迹拟合结果显示，综合考虑轨迹弯曲程度和速度对于去除异常轨迹点有明显的效果，但不能完整的处理异常数据点;通过设置权函数，运用差分和最小二乘法的思想，提高了轨迹拟合的准确性，但是设置权函数的作用比较局限。

参考文献

[1]孙川，吴超仲，褚端峰，等.基于车联网数据挖掘的营运车辆驾驶速度行为聚类研究[J].交通运输系统工程与信息，2015，15（06）：82-87.

[2]陈锦阳，刘良旭，宋加涛，等.基于R-tree的高效异常轨迹检测算法[J].计算机应用与软件，2011，28（10）：34-37.

[3]李红岩.车辆轨迹异常检测应用研究[D].长春：长春工业大学，2019.

[4]姚连璧，钱瑾斐.基于移动最小二乘法的轨迹拟合切线方位角计算[J].同济大学学报（自然科学版），2018，46（11）：1589-1593.