三光路结构的调频连续波重采样测距方法

张 桐，曲兴华，张福民

天津大学精密测试技术及仪器国家重点实验室，天津 300072

引 言

调频连续波测距技术是一种绝对距离测量技术，该技术采用的光源为波长连续变化的等效宽光谱光源，光信号经外差相干获取测量距离。 由于大带宽连续调频和外差相干叠加的特点，该技术具有较高的测距分辨率，灵敏度和信噪比，测量过程无需靶镜等合作目标的帮助。 上述优点使得调频连续波测距技术在精密制造[1]，光纤通信[2-5]，OCT成像[4-5]等领域都有较广泛的应用价值和较好的应用前景。

调频连续波测距技术常采用线性调制方式，由于外界因素的影响，实际的频率调制过程为一个非线性过程[6]，由调频信号相干迭加产生的拍频信号的频谱会引入许多其他的频率成分，掩盖真实的距离谱线，无法读出正确的测量结果。 常见的抑制扫描非线性的方法主要有两类，一类是主动型抑制方法，该方法采用闭环反馈技术检测激光的瞬时频率相对参考频率的误差，迫使激光器的调制速度稳定在参考速度附近[7-8]。 该方法设计难度较大。 另一类是被动型抑制方法，该方法通过辅助干涉仪代替光谱仪的作用，实时标定激光的瞬时频率，并对测量信号进行等频率间隔重采样，标定速度比光谱仪更快，可以做到实时标定校准。 重采样的方法主要有两种，一种是插值重采样及触发点重采样。 插值重采样法通过多项式相位的高阶模糊函数以及希尔伯特变换[9]等数学方法结合辅助信号标定激光的瞬时频率变化，这种方法计算较为精确，但计算量大，运算速度慢。 触发点重采样法以辅助信号的波峰和波谷位置的采样点作为时钟对测量信号进行触发重采样[10-13]，这种方法运算量较小，较为简单，在工程中较为常用。 这两种重采样测量方法有一个共同的问题，即待测物需要保持静止不动，但在实际的测量过程中，外界的振动对待测物体的位置及测量装置中辅助光纤的长度都会产生影响，对测量信号引入多普勒误差以及光纤长度对应的频率间隔误差，从而降低触发点重采样法的测量精度。 本文针对振动对触发点重采样方法的影响做了数学分析并提出了一种三光路的补偿方法对振动误差进行补偿，采用全光纤马赫泽德干涉仪作为辅助干涉光路监测光信号的瞬时频率，相对于光谱仪减小了仪器体积，提高了信号处理质量，处理速度。

1 振动误差对触发点重采样测量方法的影响

振动对重采样测距系统的影响主要有两个部分，一个是测量距离，由于外界振动的影响，待测物都会发生前后的移动，引起测量距离的变化，另一个是辅助干涉装置的延时光纤，在受到振动影响时，光纤的长度会发生相应的变化。

在受到低频低振幅振动影响的情况下，待测物的移动在一个激光频率扫描周期内可以近似看做是单方向的匀速直线运动，设μ为运动的速度，此时的瞬时测量距离对应的时间延迟可以表示为

τm(t)=2(Lm-μt)/c

(1)

激光器发出的光经过分光器1分为两路，一路进入测量干涉系统，另一路进入辅助干涉系统。 在测量干涉系统中，入射光再次分为两束，一束为测量信号，经过待测物反射沿原路返回； 另一束为参考信号，与回波信号相干叠加形成拍频。

激光器的瞬时频率为

f=f0+αt

(2)

对应的激光参考信号可以表示为

UL(t)=cos{παt2+2πf0t+φ0}

(3)

测量干涉系统中测量臂的回波信号的表达式为

(4)

回波信号与参考信号相干叠加后拍频信号的瞬时频率可以表示为

(5)

在辅助干涉系统中，信号光同样也是分成两束光并相干叠加。 信号光是瞬时光频率连续变化的宽光谱光源，辅助干涉系统起到光谱仪的作用，随着光波长的变化，拍频信号成正弦变化规律，通过拍频信号的相位可以得出任意时刻的波长信息。 辅助拍频信号可表示为：UA=cos(2πατAt)，其中τA为辅助干涉系统的光程差对应的时延，f0+αt为不同时刻光信号对应的频率，在峰值和谷值点处，光信号对应的频率间隔相等，选取峰值和谷值点(tn=n/ατA)对测量拍频信号进行重采样，重采样信号的频率为

(6)

式(6)中，第二项是由初始频率产生的固定频移项，第三项是由扫描速率产生的频率调制项，随着调制带宽的增加，频率谱逐渐展宽和变形。

重采样后拍频信号的傅里叶变换表达式为

[Fresencle(ν1)-Fresencle(ν2)]2}

(7)

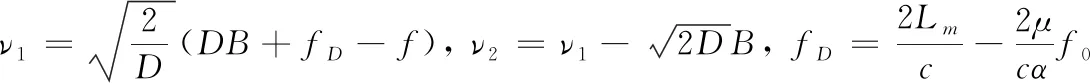
静态测量实验中，低频振动的速度都很小，幅频特性函数Smrr(f)的外形接近于一个正弦函数的频谱，频谱峰值偏移到频率调制带宽的中心位置，对应的频率为

(8)

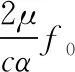
在测量装置受到外界振动影响时，辅助干涉系统中的延时光纤长度会发生变化。 由于光纤的变化速度较慢，在单次测量实验的激光频率扫描过程中可以近似认为光纤长度不变，但在不同次测量实验中的长度会有一定的改变。 设延时光纤对应的理想时延为τA，某次测量中产生的时延变化量为δτA，此时辅助干涉系统产生的拍频信号为

UA=cos[2π(f0+αt)(τA+δτA)]

(9)

设测量干涉系统的待测距离对应的时延为τm，对应的测量拍频信号为

Um=cos[2π(f0+αt)τm]

(10)

通过辅助拍频信号的峰值点对测量拍频信号进行重采样后的拍频信号为

(11)

该信号的重采样频率对应的待测距离通过泰勒展开表示为

(12)

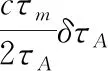
2 三光路测量装置及测距方法

为了消除实验平台振动以及光纤振动对测量结果的影响，研究中提出了一种三光路测量装置，在等频率间隔重采样测量系统的基础上增加了两个相对位置固定不变的部分反射镜。 如图1所示，三光路测距装置的基本结构由两个并联的干涉装置组成，一个是测量干涉装置，另一个是辅助干涉装置，测量干涉装置的发射光经过环形器和准直透镜发出，出射光透过两片部分反射镜MB1和MB2，经靶镜MT反射再次透过两片部分反射镜进入测量干涉装置。

图1 三光路测距系统

部分反射镜MB1和MB2以及反射镜MT放置在同一实验平台上，两镜片MB1和MB2之间的位置固定不变。 出射光在反射镜MB1处被分为两束，IMB1R反射回测量系统，IMB1T透过反射镜MB1，在MB2处又被分为两束，反射光IMB2R透过MB1回到测量系统，透射光IMB2T被靶镜MT反射透过部分反射镜MB1和MB2回到测量系统。 测距信号接收端同时获得来自两个部分反射镜以及靶镜的合成光信号。

距离测量方法。 第一步： 识别镜片位置。 用该实验装置读取经靶镜MT，部分反射镜MB1和MB2反射的合成回光信号，对该信号做傅里叶变换，在频谱上会出现三个信号最强的峰值，然后依次遮挡靶镜MT，部分反射镜MB1和MB2，观测哪一个峰值消失，以此识别出三块镜片在频谱中的位置fMT，fMB1和fMB2。

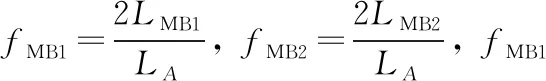
(13)

第三步： 以部分反射镜MB2的绝对距离为测距系统的起点，以靶镜MT相对部分反射镜MB2的距离为靶镜的实际测量距离。

LTC=LMT-LMB2=(fMT-fMB2)LA

(14)

通过(LMB2-LMB1)/(fMB2-fMB1)实时的标定辅助干涉系统的光程差，补偿了振动对辅助光纤长度带来的影响，fMT-fMB2消去了由振动等因素影响的共模误差。

3 结果与讨论

为了对比补偿方法对振动的抑制效果，在实验平台上放置一个偏心电机模仿振源，使光学平台处于振动的干扰环境下，通过光纤测振仪对光学平台沿测量光方向的横向振动分量进行实时监测，测量结果如图2所示。

图2 实验平台振动测量值

由图2可知，在偏心电机转动的情况下，实验平台沿测量光路的方向会发生一个微小的振动，导致测量干涉仪光纤的长度发生变化，从而使测量光纤的输出信号值呈周期性的变化规律。 在此环境下开展三光路补偿测量实验和对比实验，实验步骤如下。

(1) 反射镜MT位置固定不动，用上述三光路测量方法测量MT到MB2之间的距离，测量次数30次，测量结果作为补偿后的测量距离值，与此同时在反射镜MT和MB2旁边安装导轨和激光干涉仪，调节导轨和激光干涉仪的出射光与三光路测量装置的出射光平行，用激光干涉仪标定MT到MB2之间的距离。

(2) 为了对比三光路测量方法的补偿效果，撤掉部分反射镜MB1和MB2，移动靶镜到MB2处，使用重采样测量装置测量MB2所在位置的距离30次求取平均值近似作为该处的标准距离。

(3) 移动靶镜到MT处，使用重采样测量装置测量MT所在位置的距离，用MT的距离减去MB2所在位置平均值的距离作为MT与MB2之间的距离，重复该步骤30次，测量结果作为补偿前的测量距离值。

(4) 反射镜安装在导轨上沿导轨移动，每移动一段测量反射镜的移动距离一次，总共移动十段，与此同时用激光干涉仪标定反射镜的移动距离。

图3是由三光路测量装置测得的合成信号频谱图，图中的3个谱峰从左到右分别对应部分反射镜MB1和MB2以及靶镜MT在同一时刻的测量距离。

图4(a)为重采样测量系统测得的反射镜MT与MB2之间的距离，其中红线为通过重采样测量方法测得的距离值，蓝线为激光干涉仪测得的距离值，绿色点线为重采样方法测得的平均值，紫色点线为标定的平均值。 图4(b)为三光路测量系统测得的反射镜MT与MB2之间的距离，其中红线为通过三光路补偿测量方法测得的距离值，蓝线为激光干涉仪测得的距离值，绿色点线为三光路补偿测量方法测得的平均值，紫色点线为标定的平均值。

图3 三光路实验测量装置的频谱图

图4 MT反射镜与MB1部分反射镜之间距离的测量结果

图5是三光路系统和重采样系统对反射镜MT与MB2部分反射镜之间距离的测量误差，其中红线为重采样方法的测量值相对激光干涉仪测量值的误差(即补偿前的测量误差)，蓝线为三光路补偿方法的测量值相对激光干涉仪的误差(即补偿后的测量误差)，红色点线是补偿前测量标准差，蓝色点线是补偿后的标准差。 补偿前的标准差为23.6 μm，补偿后降到了11 μm。

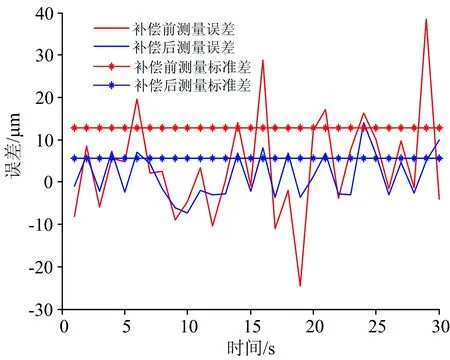
图5 三光路系统和重采样系统的测量误差

图6是由三光路测距系统测得的MT反射镜在直线导轨上的移动距离，并用激光干涉仪对其进行标定，蓝线为距离测量值，红线为三光路测量结果相对激光干涉仪的绝对误差，其中最小绝对误差为19.5 μm。

图6 三光路测量系统对直线导轨移动距离的标定结果

可以看到三光路测量系统及补偿方法有效的降低了测量距离的标准差，但是补偿后还存在残余误差，这主要是由于部分反射镜MB1与反射镜MT不在同一个位置，两个反射镜受到的平台振动有一定的差异，另外由于两反射镜的距离不同，两反射镜的多普勒误差不在同一时刻，此时两误差的大小存在差异。

4 结 论

分析了振动对重采样测量系统的影响规律，由于振动的影响，待测物的位置以及辅助干涉仪的光纤长度都会发生变化，对测量结果引入多普勒误差和重采样频率误差，降低测距结果的精度。 在静态测量实验中，受外界微小振动影响的情况下，信号的频谱不会展宽并发生畸变，但测量精度会下降。 针对振动对测量结果的影响，研究并提出的三光路的补偿测量方法，通过一个测量靶镜和两个部分反射镜在测量信号频谱中产生一条距离谱线和两条参考谱线。 通过距离谱线与参考谱线的差动算法补偿多普勒误差的影响，通过两条参考谱线实时标定辅助干涉仪的光程差。 实验证明这种方法将重采样测量系统的标准差从补偿前的23.6 μm降到了补偿后的11 μm，有效地提高了系统的测量精度。