应用于管壳式换热器热工水力数值模拟的多孔介质算法
陆道纲,王 雨,*,袁 博,隋丹婷
(1.华北电力大学 核科学与工程学院,北京 102206;2.非能动核能安全技术北京市重点实验室,北京 102206;3.长江勘测规划设计研究院,湖北 武汉 430010)
管壳式换热器在工程中应用十分广泛,其类型多样,内部结构各不相同,因此与实验研究相比,数值计算方法省时省力且具有可重复性。1974年,Patankar和Spalding[1]首次提出利用多孔介质的概念对壳侧流场进行数值模拟,引入体积孔隙率并考虑分布式阻力对流场的影响。在此基础上,Sha[2]引入了表面渗透率解释说明了液态金属换热器中支撑板、传热管等对流场的阻碍作用。Prithiviraj和Andrews[3]开发了三维计算程序HEATX,该程序物理模型采用了Patankar提出的分布式阻力概念,结合表面渗透率和体积孔隙率对换热器管侧进行建模。Ferng等[4]提出了一个三维计算流体力学沸腾模型研究蒸汽发生器二次侧不同工况下的热工水力特性。蒸汽发生器二次侧传热管被看作多孔介质,二次侧两相混合流被视为拟单相流,并假设其为物性参数可变化的可压缩流。可见,许多学者在采用数值计算方法对管壳式换热器相关问题进行研究时,均利用了多孔介质模型。尤其对于核电厂蒸汽发生器,其传热管数目众多且结构复杂,可运用多孔介质方法进行适宜的简化模拟。但不同的网格划分方法,每个控制体积的表面渗透率和体积孔隙率也会不同,所以多孔介质系数的计算方案十分重要。
KAERI等[5]在CUPID的基础上,开发了蒸汽发生器热工水力分析程序CUPID-SG,该程序在模型的入口、中间和出口处分别取多孔介质系数为0.0、0.5、0.9,3处的流体温度也被设定为固定常数。程序与ATHOS3计算结果和瑞士FRIGG试验的结果进行了对比,结果符合良好。但多孔系数并不符合真实情况下的数值,该程序仍需进一步细化。邓斌等[6]设计了一种计算多孔介质特性参数的算法,将传热管截取控制体积单元边界线的情况总结为16种位置关系。计算时对每个控制体积进行扫描判断其与传热管的位置关系,再选取相应的计算公式进行系数计算,但该方法相对较为繁琐。
为能快速且真实地反映管壳式换热器中两相流的热工水力特性,本文介绍一种适用于直角坐标和柱坐标系的大型管壳式换热器各向异性的多孔介质系数自动生成程序。
1 基于多孔介质模型的气液两相流控制方程
管壳式换热器的壳侧多为气液两相流动,流动情况复杂,为更真实反映流场流动情况,本文在多孔介质模型的基础上结合两相流模型给出了统一的控制方程(式(1)),包括气相和液相的连续方程、动量方程和能量方程。为使方程封闭,方程源项需辅助方程进行计算。控制方程中各源项表达式列于表1[7]。
(1)
式中:α为空泡份额;ρ为密度,kg/m3;u、v、w分别为周向、径向和轴向的流速,m/s;下标k表示气相或液相;fv、fθ、fr、fz为多孔系数,分别表示体积孔隙率及周向、径向和轴向的表面渗透率;θ、r、z分别为周向、径向和轴向的长度,m;Sφ为方程源项;Γ为扩散系数。
表1中:μ为流体动力黏度,Pa·s;λ为导热系数,W/(K·m);cp为比定压热容,J/(kg·K);T为温度,K;p为压力,Pa;M为相间质量转移速率,kg/(m3·s);MX为由相间质量转移引起的动量变化;R为分布式阻力;Q为二次侧流体热源。
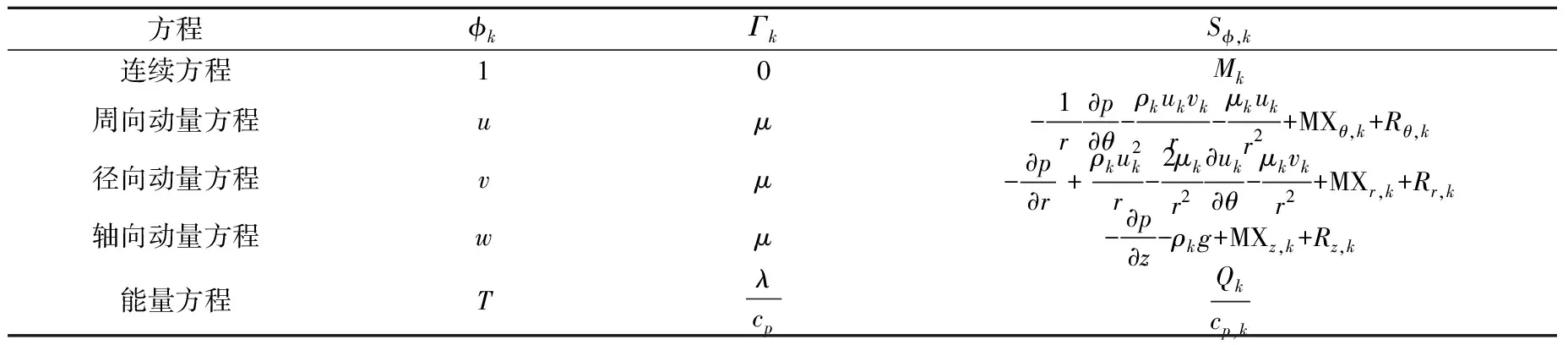
表1 控制方程源项表达式Table 1 Governing equation source term expression
2 多孔系数的计算方案
多孔系数的计算参数主要是体积孔隙率和表面渗透率。以大亚湾核电站蒸汽发生器为原型,解释说明多孔系数的计算方案。大亚湾蒸汽发生器内部共有4 474根倒U型传热管[8],以正方形排列成管束。传热管外径为19.05 mm,管间距为27.43 mm,下筒体直径为3 446 mm,管束套筒半径为1 543 mm。
首先根据模型建立坐标系网格,确定网格中心坐标,并记录网格尺寸、网格体积和柱坐标系中3个方向的投影面积。网格与传热管的位置关系(横截面)如图1所示。图中阴影区域即为气液两相流流通区域。
其次循环计算体积孔隙率和表面渗透率。对全局传热管中心坐标进行扫描,判断是否落入有效区域。有效区域表示若传热管中心坐标在此区域内,则此控制体网格被该传热管截到。图2中虚线内部为有效区域,有效区域为控制体网格四周各扩展1个传热管半径距离的区域,Δr为网格径向尺寸,Δθ为网格周向角度,d为传热管外径。

图1 网格内多孔介质示意图Fig.1 Schematic diagram of porous media in grid
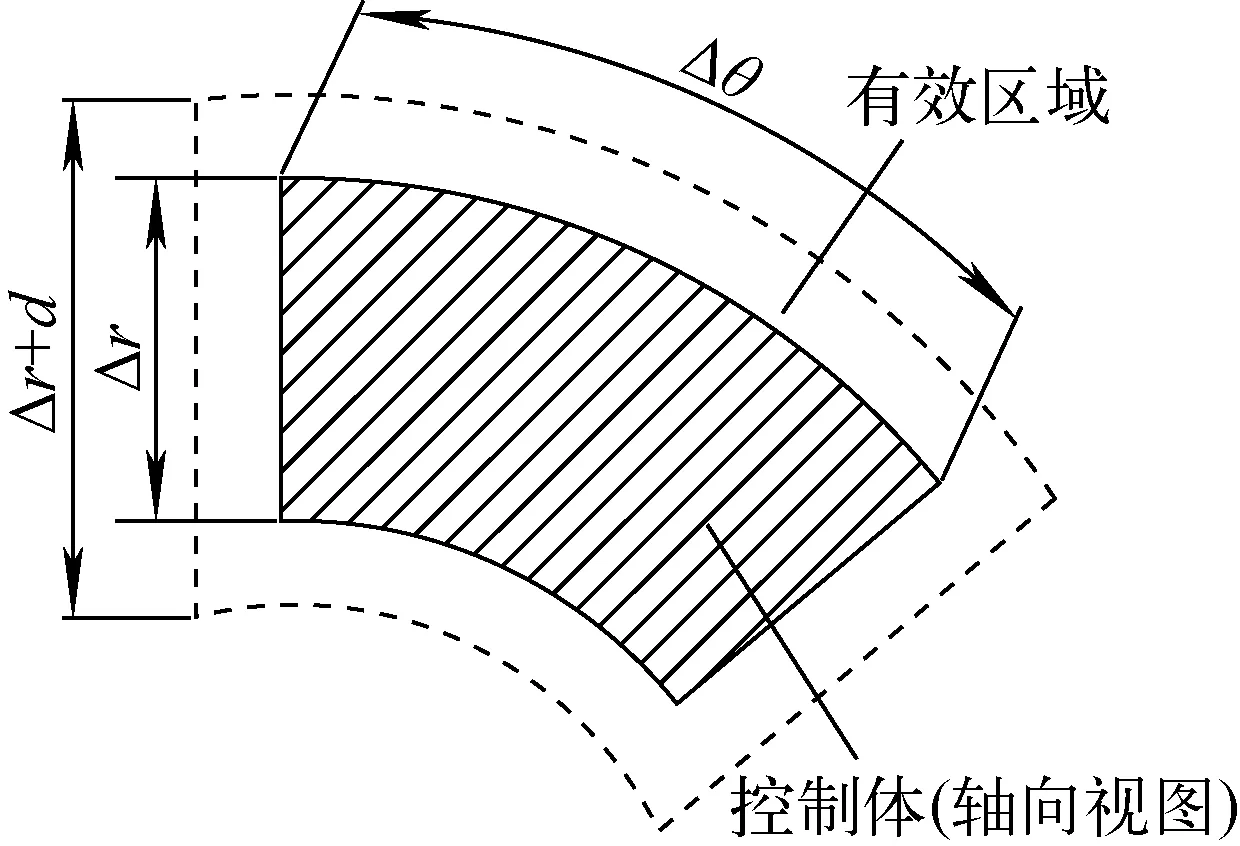
图2 网格有效区域示意图Fig.2 Schematic diagram of grid effective area
2.1 计算体积孔隙率
从第1个传热管开始扫描,若循环中检测到第n个传热管中心坐标位于有效区域内,则调用散点生成程序,该程序以此传热管中心坐标为中心,在传热管直径范围内均匀分布N个点,并记录点坐标。按顺序扫描散点并判断散点坐标是否位于控制体内。假设有M个坐标点位于控制体内,则此传热管占据控制体的体积V1(式中Δz为网格轴向尺寸)为:
(2)
逐次扫描所有传热管,判断控制体网格是否被传热管截到。将在此网格内的所有传热管体积加和,即为网格内的所有传热管体积Vs。根据体积孔隙率定义计算fv。式(3)中下标f、 s分别代表两相流流体和传热管。
(3)
计算时,若要提高体积孔隙率的精确程度,可适当增加传热管直径范围内的散点数量。
2.2 计算表面渗透率
判断位于网格有效区域内的传热管数量不为0,那么则记录位于控制体网格有效区域内的传热管数目及径向坐标。
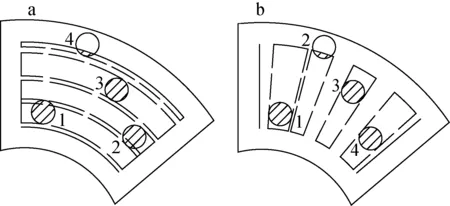
a——周向投影; b——径向投影图3 传热管投影示意图Fig.3 Schematic diagram of heat transfer tube projection
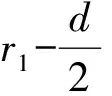
根据表面渗透率定义,则周向表面渗透率为:
(4)
(5)
其中,θ、r分别为周向和径向的方向矢量。
2.3 计算方案流程
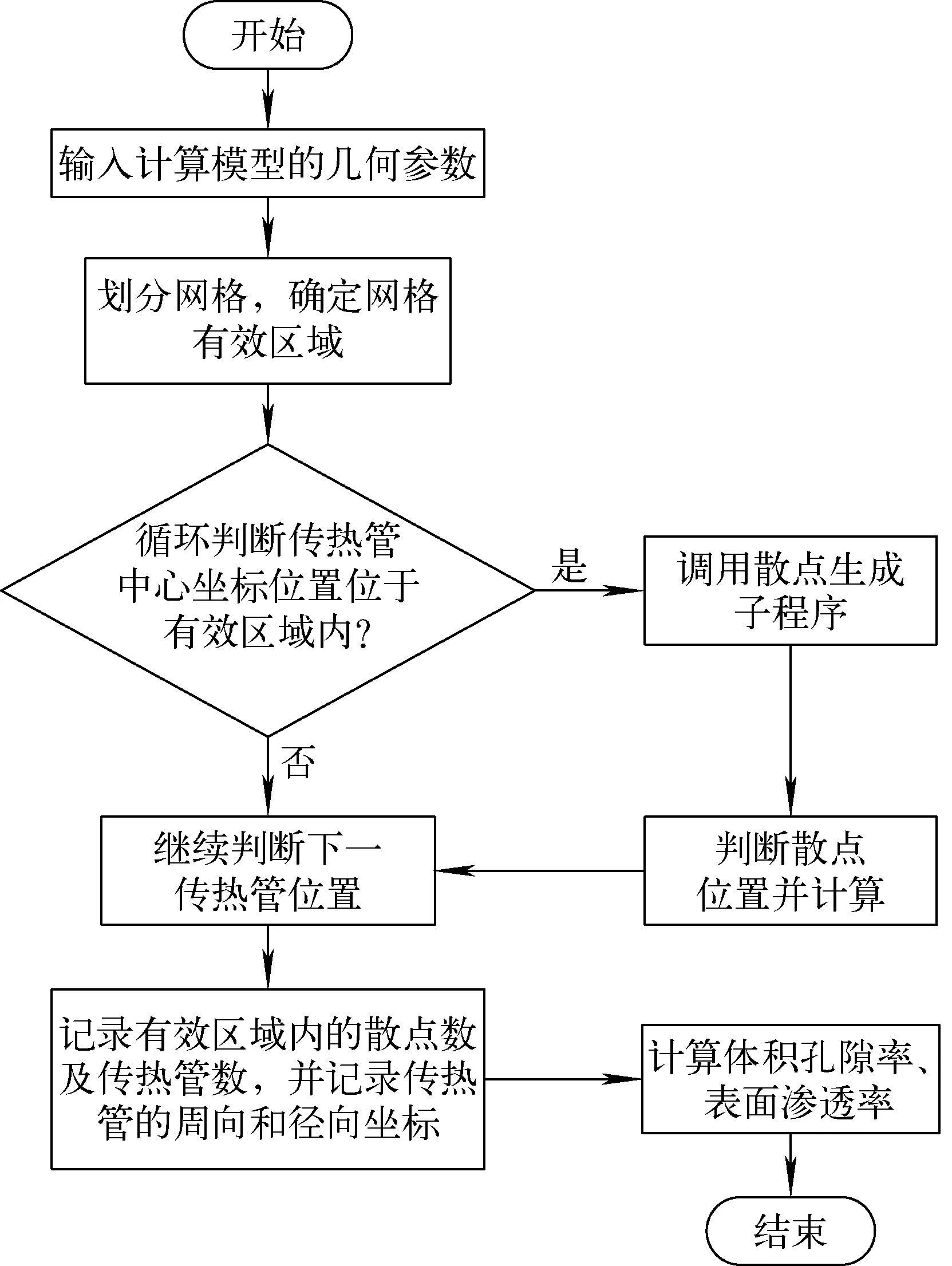
图4 计算方案流程图Fig.4 Flow chart of calculation scheme
多孔系数的计算方案完整流程控制图如图4所示。该程序可用于直角坐标和柱坐标的大型管壳式换热器各向异性的多孔介质系数自动计算,并且多孔系数会随着网格生成方案的改变而更新。
3 计算方案验证
3.1 算例实施
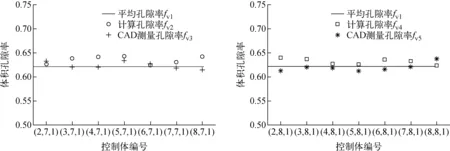
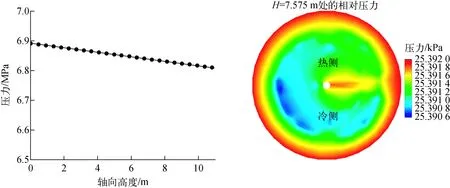
选择网格(3,7,1)作为算例,如图5所示。选取1/4的网格划分横截面图,(3,7,1)网格内阴影区域为气液两相流流通区域,其余为传热管。根据以上计算方案可得到该网格中心坐标(θ,r,z)为(0.436 3 rad,0.733 7 m,0.025 0 m),控制体尺寸为Δθ=0.174 5 rad,Δr=0.081 6 m,Δz=0.050 0 m,网格体积5.223 7×10-4m3。周向、径向面积分别为Aθ=4.080 0×10-3m2,Ar=6.401 5×10-3m2。网格有效区域为0.428 7 rad<θ<0.443 9 rad、0.724 2 m 图5 算例示意图Fig.5 Schematic diagram of example 根据传热管中心坐标位置判断出有15根传热管位于有效区域内,即(3,7,1)网格被15根传热管截到。以这15根传热管坐标中心为中心均匀建立40个离散点,经判断有556个点落于控制体内,那么实际固体所占体积为15根传热管的556/600,可求该控制体内传热管体积为1.980 9×10-4m3,则该网格的体积孔隙率为0.620 3。15根传热管在周向和径向上的投影完全覆盖网格在该方向的面积,则其周向、径向表面渗透率为0。 1) 多孔系数验证 为验证多孔系数生成方案的正确性,本文以大亚湾蒸汽发生器为原型,应用以上多孔系数计算程序计算在本文网格划分方案下的体积孔隙率。共选取14个网格,是从(2,7,1)至(8,7,1)周向上连续7个网格和(2,8,1)至(8,8,1)周向上连续7个网格,计算孔隙率分别设为fv2、fv4;同时在CAD软件中利用测量面积工具分别测量落在网格内所有传热管的横截面积以及该网格的轴向面积,进而求得体积孔隙率,相应网格的体积孔隙率设为fv3、fv5;且根据Yoon等[9-10]提到的算法计算平均孔隙率fv1。 根据文献[9-10],大亚湾蒸汽发生器的平均体积孔隙率为: (6) 将3种结果进行对比,对比结果如图6所示。从图6可看出,不同控制体的体积孔隙率互不相同,因为控制体内截到的传热管数目和位置关系不尽相同,导致体积孔隙率有所差异。但总体来说,多孔系数计算程序得到的体积孔隙率的值与CAD测量的真实值符合良好,最大误差仅为4.5%。而且计算值和测量值基本均分布在平均孔隙率周围。如若要提高计算精准度,可通过增加传热管中心坐标直径范围内的散点数量来减小误差。 图6 体积孔隙率计算结果Fig.6 Calculation result of volume porosity 2) 数值模拟结果及验证 为进一步研究GTG多孔系数计算方法在管壳式换热器热工水力数值模拟中的有效性,本文运用此方法,对蒸汽发生器二次侧管板至汽水分离器之间的流场进行了三维瞬态数值模拟。3个方向入口流速分别为0.01、0.01和1.33 m/s,入口温度为543.15 K,入口处空泡份额为0。设置压力出口边界,无滑移壁面边界条件且壁面温度保持不变,选取t=5 s时刻的流场进行分析。 图7为二次侧流场液相和气相流体的平均速度沿轴向变化示意图。丁训慎[11]在其研究中提到管束出口处的汽水混合物流速为6.71 m/s, Li等[12]研究中给出汽体出口速度为6.5 m/s左右,液体出口速度为6 m/s左右。本文数值模拟结果显示汽体出口速度为6.9 m/s,液体出口速度为6.2 m/s。参考以上出口速度,该模拟结果合理。在流体沸腾初期,产生的汽体受浮升力影响,且自身所受流阻较小,因此汽体速度上升较快。汽体沿轴向上升流动时拖曳液体向上运动,所以气液两相流体速率变化基本相同。图8示出了二次侧平均温度轴向变化图以及对称面上的温度分布云图。与Cong[13]利用漂移流模型研究蒸汽发生器二次侧流场得到的温度分布规律相似,由图8可看出,二次侧给水温度在管壳两侧之间剧烈的传热影响下迅速上升,并且很快达到饱和温度556 K,在沸腾达到稳定后,流场温度保持饱和温度不变。从温度分布云图可看出,热侧流场温度上升先于冷侧。图9示出了二次侧压力轴向变化图以及轴向高度为7.575 m处相对于出口边界的压力分布云图。入口压力为6.891 MPa,出口压力边界为6.81 MPa,流场压力在逐渐降低,总压降为0.08 MPa,符合大亚湾蒸汽发生器的设计参数。从压力云图可看出,热侧的相对压力略大于冷侧,这是由于热侧换热剧烈强于冷侧,因此流体流速更快,导致热侧相对压力大。 图7 二次侧流场速度分布Fig.7 Velocity distribution in secondary side 图8 二次侧温度分布Fig.8 Temperature distribution in secondary side 图9 二次侧压力分布Fig.9 Pressure distribution in secondary side 在管壳式换热器热工水力数值模拟中,为使多孔介质模型更真实准确地反映壳侧流场,本文提出了一种适用于管壳式换热器三维热工水力数值模拟的多孔系数计算方法GTG。该方法与网格和换热管几何参数有关,其基于网格参数和换热管位置参数计算网格内换热管数目,进而计算体积孔隙率;又使用区域缩短法计算控制体的表面渗透率。 运用此方法,以大亚湾蒸汽发生器为原型,选取14个网格计算其多孔系数,并与利用CAD软件测量的真实值进行对比,结果表明计算值与真实值的最大偏差为4.5%。(6,7,1)网格多孔系数计算值和真实值偏差仅为0.4%,几近相等。并且计算值基本分布在平均体积孔隙率周围,计算值结果和真实值符合良好。又基于该方法对蒸汽发生器二次侧流场进行了数值模拟,并与同类研究结果进行了对比验证,验证结果良好。总体来说,本文提出的计算多孔系数的方法是有效的。
3.2 方案验证


4 结论

