基于不同环境下治涝工程效益估算方法探析
张志军
(沈阳市新民市农业技术推广与行政执法中心,沈阳 110300)
0 引 言
涝灾是指由于不能及时排除过多的地表降水而引起承灾体浸泡,当承灾体的承载能力小于积水时间、积水深度的情况下,造成承载体价值、功能以及国民经济损失的灾害。根据耐淹深度和抗浸泡时间可反映承载体的承载能力,因此确定的承载体其最终的成灾度主要由淹没深度和浸泡时间决定。承载体的承载能力、积水状况与最终的成灾度存在密切的关系,而积水状况不仅与涝水外排的承泄区水位、排水系统、水系调蓄能力、涝区下垫面条件等孕灾环境相关,而且与降水量的大小有关。所以,承灾体、孕灾环境和降水量的改变,均可引起成灾度和涝灾损失值等发生相应的变化。
随着时间的变化涝区内的状况也可能发生改变,承灾体的空间分布、数量、种类等也可发生相应的改变。如,涝区下垫面产汇流条件随着城市的不断发展发生改变,且产业结构调整和城市化进程也会对承灾体的承载能力、价值总量等造成影响。另外,涝区外的承泄区水位抬高、面积缩小等孕灾环境也会产生一定的变化,海域或感潮河段的承泄区水位往往具有随机性。一般地,涝水能够自排的条件为涝区水位大于承泄区,若不满足该条件则只能强排涝水。
治涝工程建设具有社会、环境和经济效益,其中经济效益又进一步分为直接和间接效益。文章仅考虑治涝工程的直接经济效益,这主要体现在治涝工程能够降低涝灾损失的程度,即在保持孕灾环境和承灾体不变的情况下,治涝项目的实施所能减少的涝灾损失。若承灾体和孕灾环境在治涝前后发生变化,则涝灾损失值就不具备可比性。所以,假设无治涝工程情况下治涝措施的实施能够减少的涝灾损失应为变化环境下治涝效益。当前,用于治涝效益分析的暴雨笼罩面积法、实际年系列法、内涝积水量法和雨量涝灾相关法等不完全或无法适用于变化环境条件。虽然频率曲线法能够以数学期望值反映各频率暴雨引起的涝灾损失,但由于未考虑承泄区各水位可能与不同频率暴雨的遭遇情况,因此必须赋予新的内涵。实际上,承泄区的各种水文均可能与任一频率暴雨遭遇,因此各水位遭遇下的承泄区涝灾损失期望值应包含于各频率暴雨导致的涝灾损失[1]。
当前,国内关于治涝效益的研究相对较好,且考虑了变化环境的治涝效益估算方法的研究更少。郭琦等根据排涝效益、涝灾损失和涝灾成因特点,重新定义了涝灾和临界降雨量的概念,并提出了切实可行的估算方法;贾仁甫、朱旭萍等研究了涝灾损失估算方法和流域防洪体系治理效益;苏布达等基于GIS格栅数据对荆江分洪区的淹没范围、水深、淹没面积以及可造成的损失展开模拟和分析。现有研究主要集中于洪水灾害的评估方法,因此为适应不断发展变化的环境有必要研究变化环境的治涝效益估算方法[2-4]。文章运用GIS技术、Copula函数构建了涝区数字高程模型和承泄区水位与涝区暴雨联合分布,在此基础上建立了变化环境下治涝效益分析模型。根据遭遇组合水位下的承泄区和涝区暴雨积水过程估算了涝灾损失,通过计算各种组合下的不同工况的涝灾损失期望值,科学准确的确定治涝效益,然后以新民市境内某一涝区为例分析了其过程。在治涝效益估算过程中,若承泄区水位资料系列因环境的改变或暴雨资料系列因人类活动、气候的变化存在非一致性,则频率分析需采用非一致性分析方法,且需要“还现”处理原始资料。
1 变化环境下的治涝效益估算模型
1.1 构建治涝效益估算模型
假设不治理下的涝灾损失与治理下的涝灾损失数学期望值之差即为变化环境下治涝工程的治涝效益,承泄区的各种水位在理论上均可与任一频率暴雨遭遇。所以,承泄区水位和涝区暴雨全部可能组合下的涝灾损失期望值为有、无治涝工程的涝灾损失。
涝区设计历时的连续随机变量为承泄区水位Z和暴雨H,因此有、无治涝工程的涝灾损失S1和S0,对于确定的时段、确定的涝区均为随机变量承泄区水位S和涝区暴雨H的函数。令Sj=gj(h,z);(j=0,1),则Sj也为随机变量,引入概率密度f(h,z)可确定二维随机变量(H,Z)的期望值如下:
(1)
式中:z0——为可能最低的承泄区水位;
D——为坐标系下的积分区域。
所以,治涝效益B的估算方法为:
B=E(S0)-E(S1)=
(2)
根据文献介绍的方法可确定点(h,z)处承泄区水位Z和涝区暴雨H的概率密度f(h,z),通过转换计算可使得上述方法具有可行性,但涝灾损失期望值直接利用公式(1)计算仍存在较大的困难,这是由于二次积分一般无法通过初等函数直接确定、Sj=gj(h,z);(j=0,1)往往不能直接给出,所以还需要另选可行的方法。
文章对式(1)的求解考虑选用分割、近似、求和的方法,积分区域D的分割程度决定着计算结果的精度,分割越小则计算精度越高。将积分区域D利用平行于坐标轴间距为Δh、Δz的两组直线族划分为多个小封闭区域Δσi,由此可将式(1)转化为:
(3)
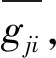
(4)
通过上述转化即可获取治涝工程的效益,其计算方法如下:
(5)
设定Δσi的长、宽分别为Δhi和Δzi,另小矩形的左下角顶点和其他3个顶点坐标分别为(hi,zi)、(hi+Δhi,zi)、(hi,zi+Δzi)、(hi+Δhi,zi+Δzi),记F(h,z)为承泄区水位Z和涝区暴雨H的联合分布,则小区域内可有:
F(hi+Δhi,zi+Δzi)-F(hi,zi+Δzi)-
F(hi+Δhi,zi)+F(hi,zi)
(6)
gj(hi,zi+Δzi)+gj(hi+Δhi,zi)+gj(hi,zi)](7)
(8)
所以,承泄区水位和涝区暴雨各种组合下联合分布、概率密度及其涝灾损失为治涝工程效益计算的关键环节。由于受文章篇幅限制,文章不再展开介绍遭遇组合的承泄区水位Z和涝区暴雨H的联合分布或概率密度,详见文献[5]。对于涝灾损失在点处的计算,其关键步骤是确定排涝调蓄在有、无治涝工程下的大小,通过模拟承泄区各种水位与各频率暴雨遭遇组合时有、无治涝工程的积水过程;然后依据涝区土地利用、地貌类型、地形特征等资料,采用GIS技术手段建立洪灾损失评估的容积-面积-水位关系曲线、各类承载体空间分布图和涝区地块功能分布图,由此确定不同淹没历时、不同淹没深度下各类承载体的面积;根据淹没深度和涝灾损失率研究成果和以淹没时间为参数的各承载体调研资料,确定治涝工程减少灾害损失的程度[6-9]。洪灾损失及其主要内容、各类损失计算方法与文献资料基本相同,主要包括:物资、设置和房屋损坏;农林牧副渔各业减产;通信、电力、交通中断、商业停业和工矿停产损失;救灾和抢排涝水费用支出等。
1.2 治涝效益分析流程
步骤一:收集整理涝灾损失相关基础资料,计算分析需要的关系曲线。其中,关系曲线主要包括容积-面积-涝水位关系曲线和以淹没时间为参数的各承载体淹没时间-涝灾损失率曲线两类,前者可通过GIS技术生成的数字高程模型确定,后者可参考现有研究资料或调查统计分析获取。
涝灾损失相关基础资料主要有各类承载体的空间分布、涝区土地利用和涝区范围内的社会经济情况等。社会经济情况又包括个分类资产值、生产成本、农业区农作物组成、土地面积、行政区划、总产、单产、稳产、人口、国内生产总值、工农业总产值及高产农田面积及产量等资料。为合理的分配各类承载体的空间分布,有必要准确掌握各产业分布特征。
步骤二:收集承泄区的水位资料系列和涝区设计历时的年最大暴雨,分析确定承泄区水位与涝区暴雨的边缘分布、联合分布及概率密度函数。
步骤三:根据联合概率密度分布和泄洪渠水位、涝区年最大暴雨等确定积分区域,合理分割积分区域。依据联合概率密度分布确定年最大暴雨量的上、下限值,在计算过程中不必设定为无穷大或零。根据概率密度分布确定承泄区水位的上限值,且上限值不大于防洪设计水位,以汛期最低水位作为下限值设定依据。
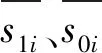
城市管网排水区的暴雨历时、积水深度、面积和量级可选用地面积水数学模型模拟确定,地面积水的涨消过程还可利用GIS技术进行动态演示;而非城市管网排水区的蓄水量变化、涝区水位变化过程,可直接由排涝调蓄演算和产汇流计算确定。给定水位下的淹没区范围和利用DEM数字高程模型确定,从而获取不同水深淹没时间、深度、面积等估测值;各功能地块治理前后的涝灾损失值可利用以淹没时间为参数的各承载体淹没深度与涝灾损失率关系确定。
2 实例分析
2.1 区域概况
新民市地处辽河下游平原区,介于E122°27'-123°20',N41°42'-42°17'之间,区域总面积3318km2。境内大部分地区地势平坦、地形开阔,北部存在少部分孤立残丘,地形特征呈自东北向西南方向逐渐升高的趋势。该地区河流水系发达、支流众多,主要有蒲河、秀水河、饶阳河、柳河、养息牧河及辽河6条河流,属于大陆性季风气候,秋冬寒冷干燥、春夏多风多雨,年均降水量604mm且时空分布均匀,年均蒸散发1651mm,平均气温7.6℃,无霜期163d。土壤类型以棕壤土为主,灌木丛、荒草坡及马尾松等植被较为常见。
境内某一涝区的原有农业用地,由于城镇化和经济建设的需要全部变为城镇用地,所以有、无治涝工程情况下全部城镇用地的涝灾损失期望值之差应为治涝工程的总体效益。涝灾损失增长与当地经济的增长相关,经济发展水平的不同所造成的涝灾损失存在一定差异,因此先计算治涝效益、涝灾损失在近期规划水平年2020年的状况[11-12]。
2.2 计算流程
1)了解以淹没时间为参数的各承灾体的淹没深度与涝灾损失的关系和各类承灾体的空间分布特征。目前新民市正处于开发建设时期,结合调研成果和涝区发展规划估计各类资产在2020年的空间分布,此项工作一般难以做到且工程量巨大,因此可采取均匀分布作近似简化处理,各类资产2020年的产值如表1所示。依据现有研究成果和调研结果,建立涝区统一的以淹没历时为调整因素、以水深要素为主的资产涝灾损失率关系,最终确定各分类资产在2020年不同淹没水深下的涝灾损失率,见表1。
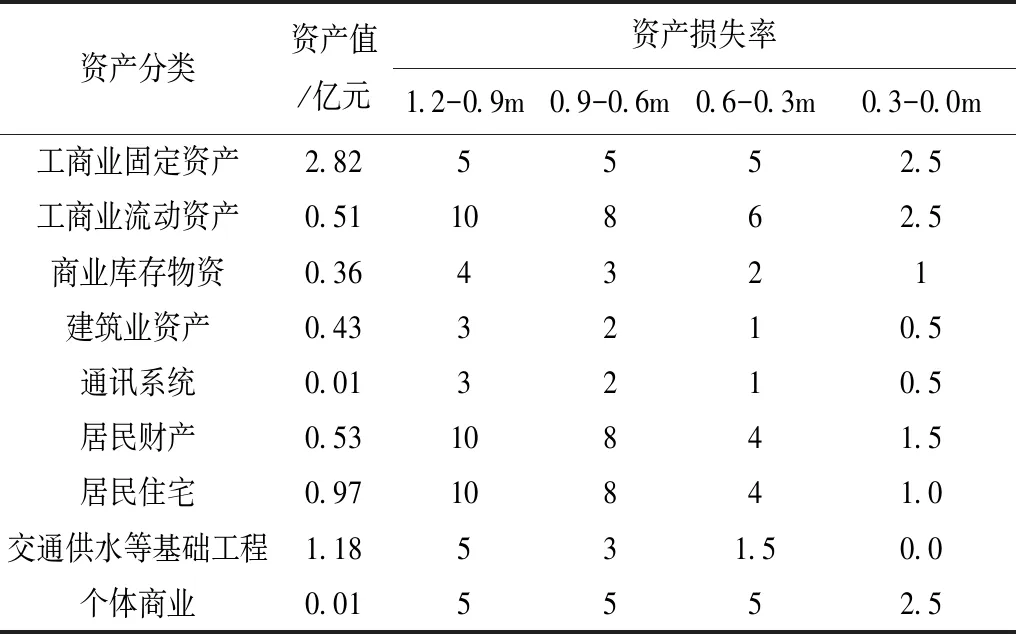
表1 不同淹没水深下的资产损失率和
2) 揭示承泄区水位与涝区年最大暴雨的遭遇变化规律,确定并隔离分割计算区域。涝区潮水位和最大一天暴雨的联合分布依据潮位站的相应潮位、雨量站1980-2018年的历年最大一天雨量分析确定,设定fH(h)、FH(h)分别为年最大一天雨量H的边缘概率密度和边缘分布,当潮水位为Z时有fz(z)、Fz(z)。
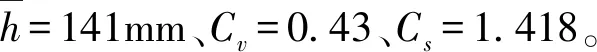

表2 年最大日暴雨量频率和潮位频率计算成果
根据文献资料推求它们的联合概率密度函数f(h,z)和联合分布F(h,z),所对应的表达式如下:
F(h,z)=FH(h)Fz(z)/[1-0.45(1-FH(h))(1-Fz(z))]
(9)
(10)
各h和z组合出现的概率大小可通过联合概率密度函数值f(h,z)来反映,按照以上计算公式可确定积分区域为60-320mm、0.65-2.05m,以承泄区5a一遇潮位2.04m和20a一遇暴雨262mm作为治涝设计组合。所以,根据治涝设计组合情况和文中所述相关公式合理分割积分区域,如图1所示。
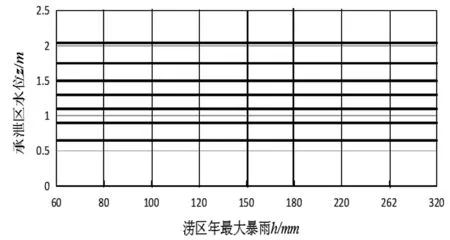
图1 积分区域分割图

若在2020年建设投产此涝区治涝工程,则排涝效益期望值b0在基准年2020年为508.2万元。由于新民市正处于经济建设和大开发阶段,对于各类资产的经济增长率难以准确的推求,为便于计算假设各类资产的增长保持相同。在不同的折现率和考虑经济年增长率j=6%的条件下,在投入运行期n=30年内该治涝工程的总效益P和年均效益b计算公式如下:
当i=7%、10%、12%的情况下,b值分别为1000.2、896.5、842.8万元,相应的P值为1.25、0.96、0.67亿元。
3 结 论
假设治涝功能情况下有治涝工程所能够降低的涝灾损失即为变化环境下治涝工程的直接经济效益,其中承泄区和涝区暴雨全体可能组合下的数学期望值为涝灾损失。所以,变化环境下的治涝效益采用传统的计算方法已不再适用,文章结合文献资料提出了能够有效解决该问题的治涝效益估算模型,得出的结论如下:
1) 新民市境内某一涝区实例分析表明,考虑了承泄区水位和涝区暴雨的治涝效益分析模型,能够准确的反映承灾体和涝区内环境变化情况,该模型更够更加客观、系统的反映治涝工程的实际效益,可为治涝方案优化设计提供一定指导作用。
2) 承泄区水位和涝区暴雨遭遇组合的联合概率密度分布图可利用Copula函数分析计算确定,并用于组合范围和积分区域的计算确定,概率权重利用联合分布计算确定。若承泄区水位资料系列因环境的改变或暴雨资料系列因人类活动、气候的变化存在非一致性,则频率分析需采用非一致性分析方法,且需要“还现”处理原始资料。
3) 若涝区周边不存在相应的水位资料和暴雨数据,则承泄区水位和涝区暴雨联合概率分布的构建受到数据资料的条件限制,因此为进一步提高分析结果的精确度未来还需要不断的积累暴雨和水位相关资料。

