基于激光红外检测信号的表面裂纹定量重构

杨 阳，邱金星，刘皓晨，裴翠祥，陈振茂

（陕西省无损检测与结构完整性评价工程技术研究中心，机械结构强度与振动国家重点实验室， 西安交通大学，陕西 西安 710049）

0 引言

为了确保关键设施结构安全运行，对表面裂纹进行检测十分重要，需要在工程实际应用中采用无损检测技术。目前应用较多的常规无损检测方法，例如超声检测、渗透检测和涡流检测，存在不能远距离对结构进行检测，检测效率低下的问题[1]。

作为一种新型的红外检测方法，激光红外检测技术运用激光热源对被测试件表面加热并利用红外相机检测记录表面的温度分布图像[2]。当激光光斑靠近表面裂纹时，其表面热流会因裂纹的存在而产生扰动，因此通过对红外图像的分析即可实现对表面裂纹的检测。与常规的无损检测方法相比，激光红外检测技术具有远距离、非接触和高检测效率的优点[3]。由于采用激光点光源作为热源，其热流主要沿表面传播，因此非常适合用于表面裂纹的检测[4]。此外，基于表面温度信号，该方法也有望实现表面裂纹的定量重构。

本文根据激光红外检测的基本原理，并基于频域叠加法和数据库策略，实现了表面温度的快速数值模拟，计算了不同裂纹尺寸下试件表面的温度分布。通过引入合适的信号特征量，基于确定论裂纹重构算法，实现了基于激光红外检测信号的表面裂纹定量重构。最后进行了红外检测实验，基于实验信号完成了对试件表面裂纹的定量重构，验证了该方法的有效性。

1 数值模拟方法

1.1 红外检测数值模拟理论

激光红外检测的导热为瞬态传热过程。根据傅里叶传热定律，对于均匀、各向同性材料，忽略其表面辐射和对流，并设内热源为零，这时热传导方程可写为如下形式：

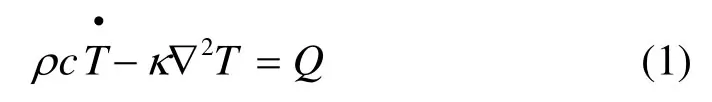
式中：ρ、c、κ分别为材料的密度、比热容和热导率；T为温度；Q表示外部热激励。

温度场的边界条件可表示为：

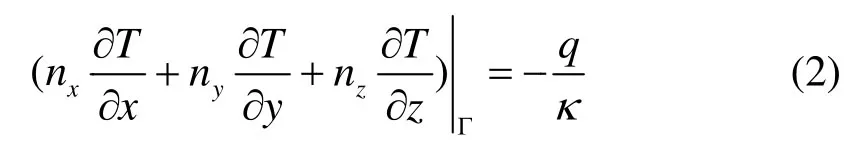
式中：nx，ny，nz为边界法向量在x、y、z方向上的分量；q为激光热源的热流密度。根据有限元方法，控制方程可离散表达为如下形式：

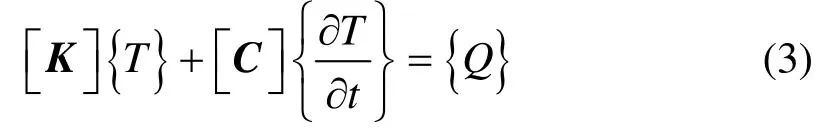
式中：[K]、[C]分别为有限元模型导热系数矩阵和比热系数矩阵；{Q}为瞬态热激励。对该控制方程可运用时域积分法进行求解计算[5]。

1.2 红外检测信号快速算法

有限元控制方程的传统时域积分法求解方法需要在整个时域上按时间步长Δt不断迭代求解计算，为保证求解的精度，Δt需保持小量，对于逆问题缺陷重构中需大量正问题计算时，其效率不高，需寻求快速准确的求解方法。作者研究组提出了针对脱粘缺陷的红外检测快速计算，该方法基于频域叠加法和数据库策略，将有限元控制方程从时域转化为频域，并进一步通过利用无缺陷数据库对方程进行降维处理，从而可大大减少求解时间[6]。本研究将这一算法拓展到表面裂纹缺陷的快速数值模拟。

对于有限元控制方程(3)，由于红外响应问题为线性问题满足叠加原理条件。根据傅里叶变换，瞬态热激励{Q}及温度{T}可表示为一系列正弦分量的叠加，因此式(3)可转换为如下形式：

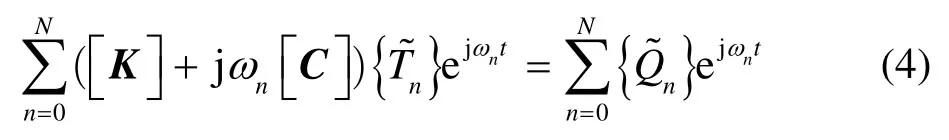
式中：N为分解的频率总个数；分别为第n个频率所对应正弦分量的幅值；ωn为第n个谐波角频率且ωn＝nωb，其中ωb是傅里叶分解的基频。有式(4)可得单个谐波频率分量对应方程为：

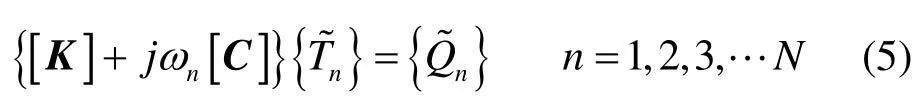
值得注意的是，对所有谐波分量运用式(5)进行求解，会导致很大的计算量。为减少计算量可采取频响函数插值策略，即选取合适的频率进行求解，而对其他谐波频率则运用插值方法进行近似处理。以上即为基于频率叠加法的红外快速模拟方法的基本思路。

为进一步提高计算效率，对于裂纹缺陷导致的红外信号扰动的快速计算可运用数据库策略。该方法基本思想是通过提前建立无缺陷模型温度场数据库将式(5)进行降维处理。对于含裂纹缺陷模型，可将节点分为3类：缺陷区域节点、非缺陷区域节点和表面节点，只有对缺陷区域节点，其控制方程(5)中的系数矩阵[K]和[C]与无缺陷模型不同，由此将含缺陷模型的控制方程与无缺陷模型作差后，整个控制方程的求解只与缺陷区域有关，即可将方程的维数降低至缺陷区域节点数，从而大大缩短方程的求解时间。对于裂纹红外重构问题，可提前建立无缺陷模型和无缺陷场数据库，运用频率叠加法进行求解，对于重构过程中不同大小裂纹的正问题计算，只需直接从数据库中取出相关参数即可，可进一步提高计算效率。

1.3 快速算法验证

为验证上述快速算法的有效性，建立表面裂纹缺陷模型并分别运用时域积分法、频域叠加法、数据库法进行了红外响应信号的计算。在建立模型时，在距离裂纹较远的区域所划分网格较大，而在裂纹附近区域网格划分较密。所用模型的几何形状如图1所示，模型网格参数和材料参数分别列于表1与表2。

图1 三维模型图Fig.1 3Dmodel

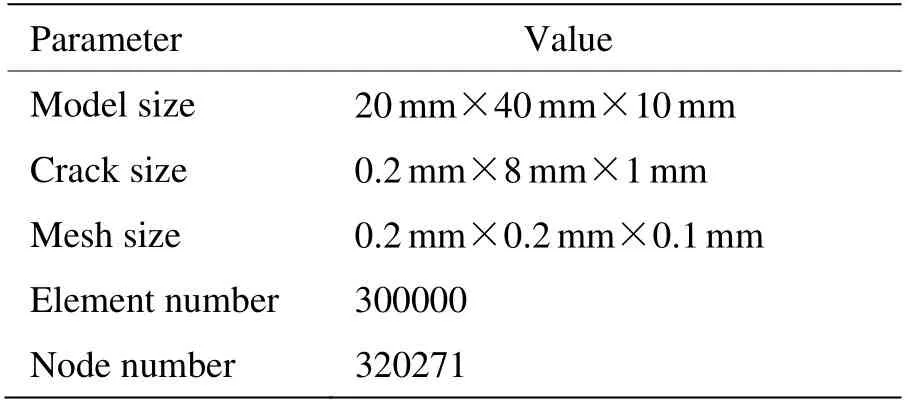
表1 模型网格参数 Table 1 Parameters of model and mesh

表2 模型材料参数 Table 2 Material parameter of numerical model

采用的热激励为2×3的激光点阵，即在裂纹两侧各布置3个激励光斑，光斑直径为2.8 mm，激励函数为g(t)=8t3e-2t2，在该激励下试件表面温度在1 s时刻达到最大值。为保证精度，时域积分法所采用的时间步长为0.01 s。而为提高计算效率，对频域叠加法进行了插值处理。在图2中给出了不同方法对中心点温度随时间的变化曲线以及1 s时中心线上各个节点的温度分布曲线的计算结果。3条曲线基本重合，从时间分布和空间分布两方面3种方法的结果具有很好的一致性，从而验证了快速算法的有效性。表3给出了不同方法的计算时间，可以看到在保证计算精度的同时，频域叠加法与数据库法相比时域积分法计算速度大幅提升，并且数据库法相比频域叠加法具有更高的计算效率。

2 表面裂纹重构方法

2.1 信号特征量选取和重构算法

影响温度场分布的主要因素有裂纹的长度、宽度、深度以及裂纹的位置。本文所研究的表面裂纹宽度很小，一般为0.1～0.4 mm，裂纹宽度不会对裂纹两侧区域的温度分布造成显著影响[7]，而裂纹的位置一般可利用红外图像分布直接确定，因此本研究将裂纹的宽度和位置视为已知，仅裂纹长度和深度进行重构。

基于确定论反问题算法，裂纹重构问题可表述为计算所得信号特征量与实验所得特征量的加权残差最小化的优化问题。优化目标函数可表示为如下形式：

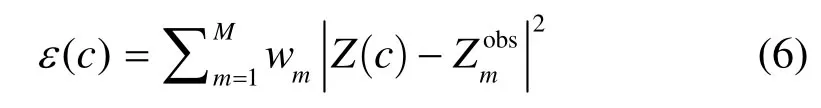
式中：c为裂纹参数向量；wm为加权系数；M为特征数据点数；Zmobs为第m个特征量数据的实测值。采取共轭梯度法对裂纹参数进行迭代更新，当残差达到最小值时，即可完成对裂纹的重构。选取合适的特征量对于重构算法的有效性至关重要。

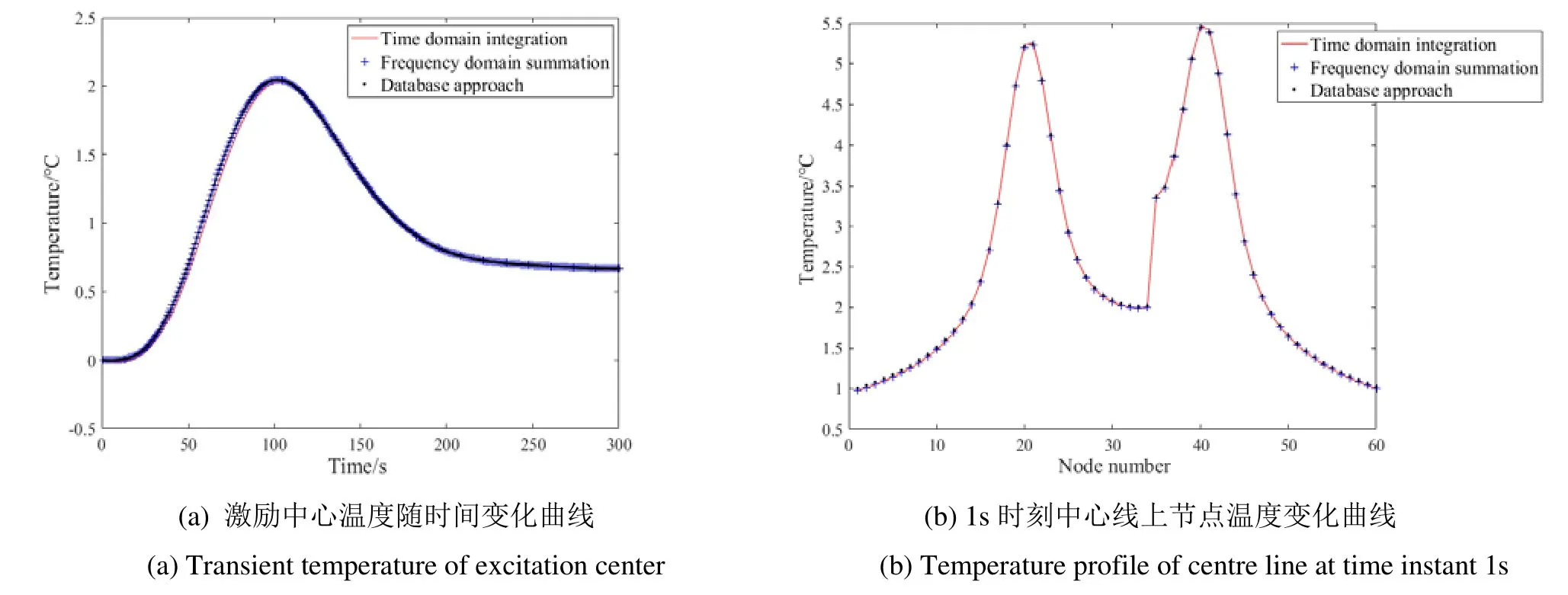
图2 3种方法计算结果对比Fig.2 Comparison of calculation results

表3 3种方法计算时间对比Table 3 Comparison of time consuming

为此针对宽度0.2 mm、长度范围2～6 mm、深度范围0～2 mm的一系列裂纹模型，对其在第1章所示激光激励下的温度相应进行了计算，并求取了当表面温度达到最大值时刻裂纹两侧节点的温差。图3为沿 长度方向裂纹两侧节点温差的分布曲线，坐标零点对应裂纹中点位置。对于不同长度的裂纹，其两侧节点温差分布有很大差别，在较短的裂纹长度方向以外区域，由于无裂纹存在其两侧节点温差非常小，而长裂纹对应的节点温差则远大于该值，因此各个节点温差值可以反映长度信息。同时随着裂纹深度的增加，其对热流的阻碍也随之增大，两侧温差增大，节点温差值可同时反映深度信息。因此针对该模型选取30个节点温差组成的向量{ΔT}作为特征数据对裂纹进行重构。这时优化目标函数为：

式中：ΔTobs为实验得到的节点温差。

为验证该重构方法的有效性，对裂纹长度分别为为2 mm、4 mm、6 mm，深度分别为1 mm、1.5 mm的6个裂纹模型的温度响应进行了数值计算，并添加5%随机噪声作为模拟实验信号，提取出相应的特征量{ΔT}进行裂纹重构。表4为相应重构结果，重构出的长度与深度均与实际值基本吻合。

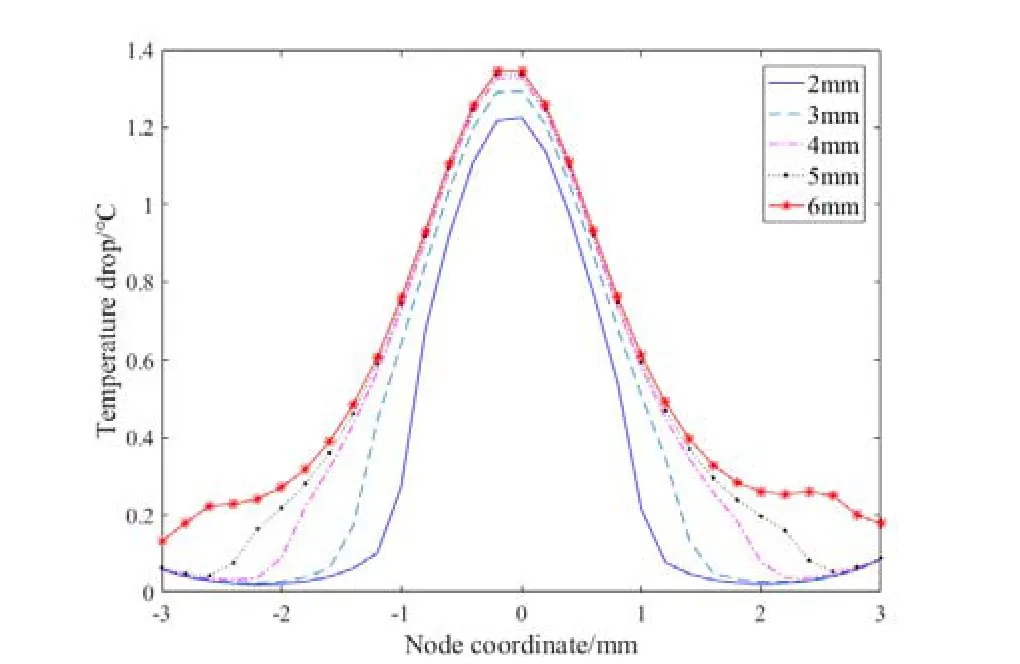
图3 不同裂纹长度下裂纹两侧温差分布曲线 Fig.3 Temperature difference across crack of different length

2.2 基于实验信号的裂纹重构

为进一步验证重构方法的有效性，进行了激光红外检测实验，实验系统如图4所示。系统主要由激光器、产生激励信号的信号发生器和采集红外图像的红外热像仪组成。裂纹试件如图5所示，裂纹深度为1.5 mm、长度10 mm、宽度0.2 mm。实验采用的激励信号为2 s正弦脉冲信号，激光器产生单光斑，其直径为4 mm，光斑中心距裂纹2.8 mm。在1.1 s时试件表面温度达到最大值，对此时刻红外信号进行滤波处理，并按照2.1节的重构方法选取裂纹两侧24个节点温差作为特征量进行重构，节点间距为0.5 mm，选取的节点区域长度为12 mm大于裂纹长度。其重构结果为长度8.5 mm，深度1.6 mm，在深度上可实现较好的重构，但在长度上重构结果与实际值出现一定偏差。这是由于不同于模拟时所采用的点阵激励，本次实验为单光斑激励，在裂纹长度边界附近其两侧温差较小，在重构中其权重过小，需寻找更优的目标函数及特征量来实现长度深度的准确重构。

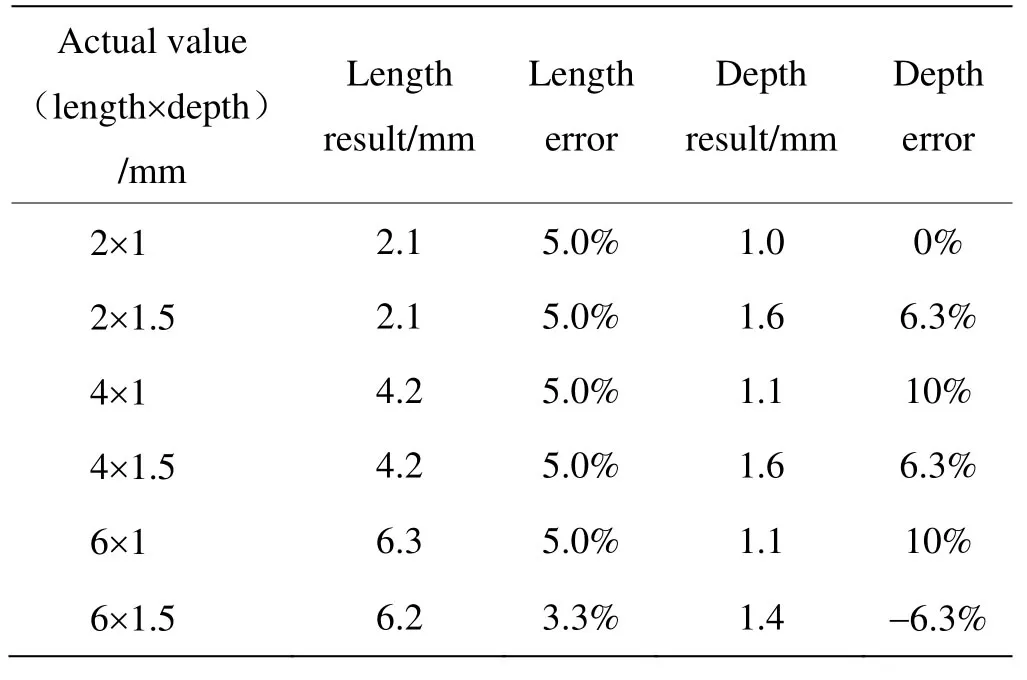
表4 采用计算数据的重构结果 Table 4 Reconstruction results for simulated signals

为了寻找合适的特征量，建立不同裂纹模型，固定裂纹深度1.5 mm，分别取裂纹长度11 mm、10 mm、9 mm和8 mm运用已建立好的数据库进行计算，研究其裂纹末端附近的两侧节点温差（15-24号测点）。由图6可以看到，开始时不同长度的裂纹节点温差几乎一致，但随着节点编号的增大，短裂纹的节点温差开始快速下降并先趋于0。虽然在远离激励处，不同长度裂纹的节点温差都在很小的量级，但由于短裂纹的节点温差先接近0，长裂纹的节点温差是其数倍。对此计算不同长度节点温差与实验值之比max{ΔT/ΔTobs,ΔTobs/ΔT}，做出一侧节点温差的比值图像，如图7所示，可以看到比值能够较好地反应出长度的变化。

因此，为增大裂纹端部温差的权重，对于两端测点（1-9和16-24号测点），选取计算值与实验值的比值max{ΔT/ΔTobs,ΔTobs/ΔT}作为特征量，而中间测点依旧采用温度差值{ΔT}。改良后的优化目标函数为：

图4 实验系统示意图Fig.4 Experimentalsetup

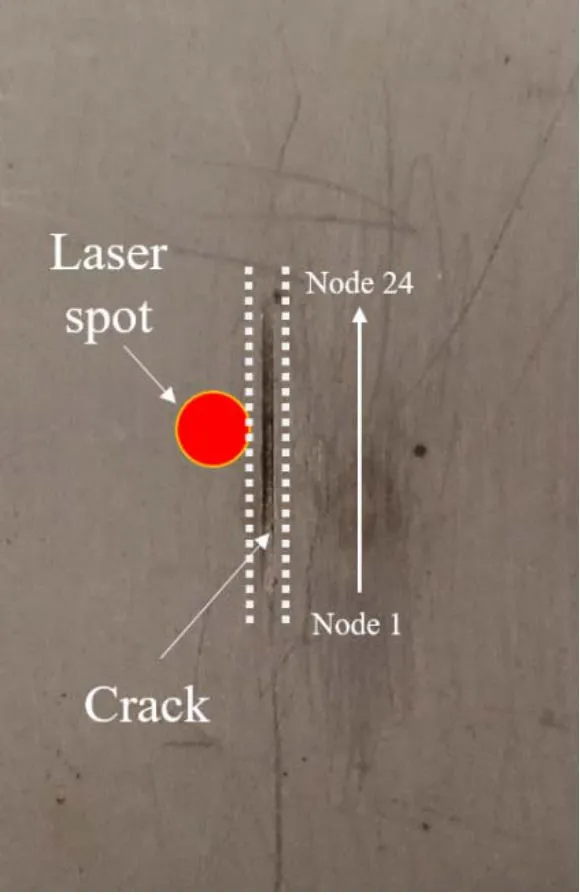
图5 裂纹试件图Fig.5 Figureof test-piece with crack

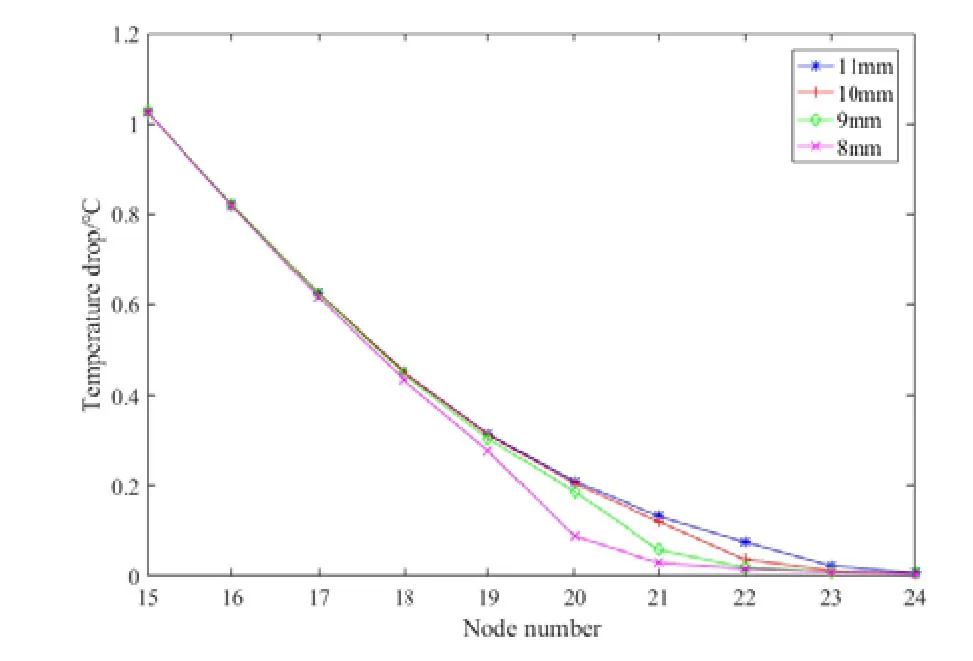
图6 沿裂纹长度方向的温差分布Fig.6 Temperature difference distribution along cra ck

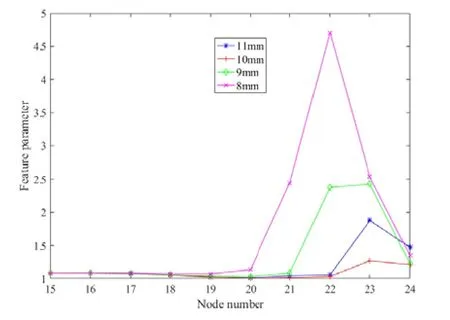
图7 沿裂纹长度方向的温差特征量分布Fig.7 Distribution of featureparameter along crack

按照式(8)目标函数利用共轭梯度法进行求解，对裂纹进行了重构。当设置初始深度0.2mm、长度6mm时，所得重构结果为裂纹深度1.58mm、长度10.6mm，与1.5mm深、10mm长的真实值基本一致。图8为模拟所得的1.1s时刻裂纹两侧温差分布曲线，可以看到重构裂纹对应检测信号的计算结果与实验结果也基本一致，进一步验证了重构结果的有效性。

3 结论

本文基于频率叠加法与数据库策略实现了表面裂纹激光红外检测信号的快速数值模拟，并通过与原有方法的对比验证了快速算法的有效性。针对裂纹长度与深度的重构，分别对不同尺寸的裂纹模型表面温度场进行了计算分析，选取裂纹两侧节点温差作为重构特征量，基于共轭梯度法开发了重构算法并以添加噪声的模拟温度信号进行裂纹重构，验证了方法的可行性。最后进行了平板试件裂纹红外检测实验，针对实验条件的特殊性，对特征量进行更新，实现对基于实测信号的有效裂纹重构。

图8 1.1s时刻裂纹两侧温差分布曲线Fig.8 Temperaturedifference acrosscrack at time instant 1.1s