永磁同步电机伺服系统控制中的自抗扰控制策略

岳尚武，季诚胜，孙德新,3

（1.中国科学院上海技术物理研究所，中国科学院红外探测与成像技术重点实验室，上海 200083； 2.中国科学院大学，北京 100049；3.中国科学院上海技术物理研究所启东光电遥感中心，江苏 启东 226200）

0 引言

永磁同步电机（permanent magnet synchronous motor，PMSM）具有转矩脉动小，调速范围大，高精度高效率，低惯量低噪声等特点[1]，自20世纪末开始在不同领域的控制系统中得到了广泛的应用[2]。在工程上，目前伺服电机控制系统最普遍采用的调速控制策略仍然是经典的比例-积分-微分（proportion -integration-differential, PID）控制，其工作原理是，根据被控量与给定参考指标的偏差，利用比例参数及积分参数，生成控制量，达到缩减误差并消除稳态误差的控制效果。PID控制策略具有结构简单，控制性能较好，参数少且物理意义明确等优点，但也带来了快速响应和超调之间的矛盾[3]。此外，PID控制策略特定参数不能适应于变化的转速范围[4]，应用于伺服摆扫电机变速跟踪时，其局限性较大，需要实时调整。

永磁同步电机是时变、强耦合性的非线性系统[5]，为适应复杂环境下的电机变速跟踪扫描，需要为永磁同步电机调速系统引入性能更好、适用性更强的控制算法，提高电机的转速响应，稳定性及抗干扰能力等系统性能。针对这一需求，韩京清教授提出了自抗扰控制技术[6]。然而，自抗扰控制也有算法参数较多，计算逼近过程产生延时等缺点。

本文在搭载成像机构做慢扫快回变速扫描成像的PMSM伺服系统中，引入了改进的自抗扰控制算法（auto disturbance rejection controller，ADRC），在简化了跟踪微分器（trace differentiator，TD）及扩张状态观测器（expansion state observer，ESO）模块的同时，保留了ADRC控制器对扰动估测的算法，既能做到电机的快速响应，又可以实时减少扰动带来的影响。最终将其实现于搭载摆扫镜的电机控制中，得到了优于PID控制的系统性能，证明了自抗扰控制策略在复杂环境下变速扫描控制的性能优势。

1 PMSM改进的自抗扰控制器设计

在不影响PMSM控制性能的前提下，忽略铁芯饱和，不计涡流和磁滞损耗及谐波，其在d-q轴两相转子旋转坐标系下的状态方程[7]写为式(1)：

式中：id、iq分别为定子电流d、q轴分量；ud、uq分别为定子电压d、q轴分量；RS为定子电阻；Ld、Lq分别为定子d、q轴电感，对于面贴式永磁同步电机，有Ld＝Lq＝L；np为PMSM极对数；φf为转子永磁体磁链；ω为电机转子角速度；TL为负载转矩；B为运动阻尼系数；J为电机与负载转动惯量。

PMSM矢量控制通常采用速度-电流双闭环结构，不考虑弱磁，控制d轴给定电流id*＝0，使d轴电流近似保持为0，此时定子电流全部为转矩电流，可以产生较大转矩并且控制简单，能够有效降低铜耗，稳定性好[8]，基于id*＝0控制法的永磁同步电机矢量控制系统原理框图如图1所示。

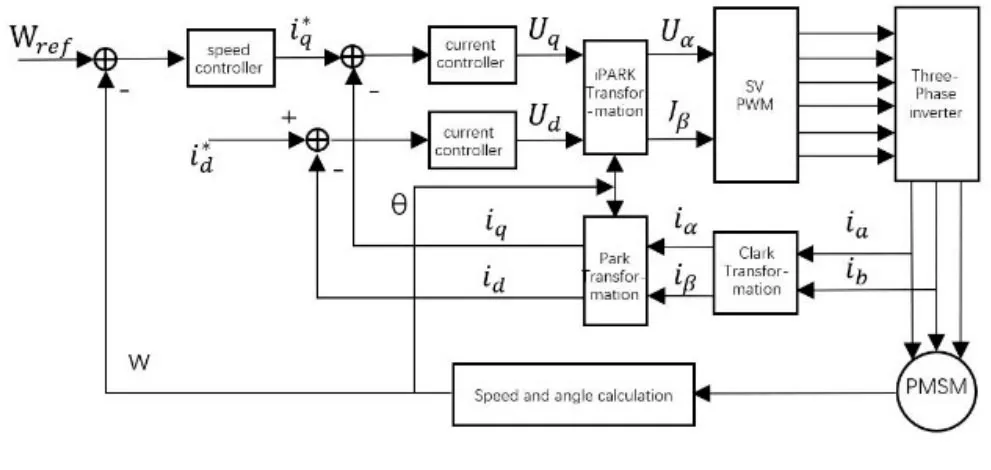
图1 PMSM速度-电流环矢量控制原理图 Fig.1 PMSM speed-current loop vector control schematic diagram

自抗扰控制保留了传统PID控制根据误差生成控制量来消除误差的核心思想，由以下3部分组成：跟踪微分器（TD），扩张状态观测器（ESO），非线性状态误差反馈控制律（nonlinear states error feed-back，NLSEF）。

对于形式如式(2)所示的一类不确定对象[6]：

式中：f(x,x˙,…,x(n-1),t)为未知函数；d(t)为未知扰动；y为系统输出；u(t)为系统控制量；b为补偿系数，各部分典型形式[9]如下：

跟踪微分器：

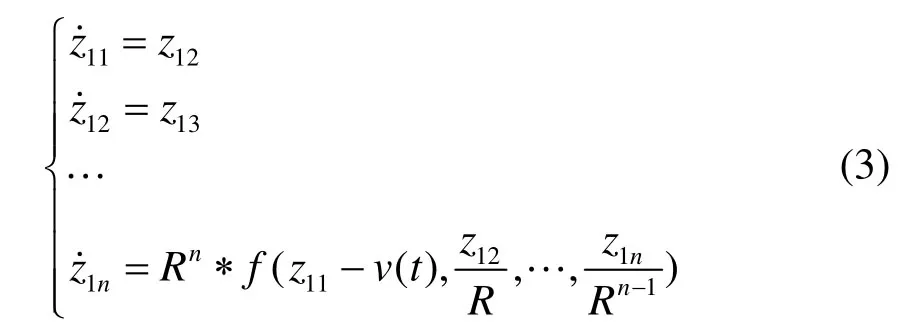
式中：z11为给定信号v(t)的跟踪信号；z11˙,12z˙,…,1nz˙为v(t)各阶广义微分；为非线性函数；R为输入信号的界，TD为参考输入v(t)安排平滑的过渡过程及各阶微分信号。

扩张状态观测器：

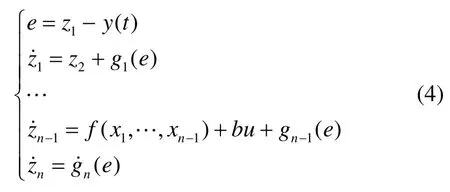
式中：ESO根据系统输出量y(t)得到跟踪信号z1和各阶微分信号zi，并扩张成一个新的状态变量进行前馈补偿，及对系统扰动量的估计zn+1；e为控制量与实际输出偏差；f(x1,…,xn－1)为未知函数，gi(e)为基于偏差e的变量；u为系统控制量；b为控制系数，这也是ADRC控制器区别于其他控制算法的部分所在。

非线性状态误差反馈控制律：

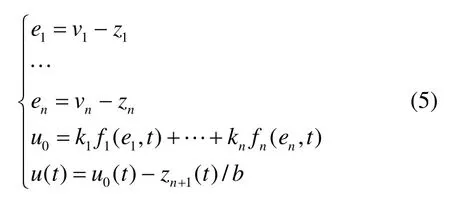
式中：ei(i＝0,1,…,n)为跟踪信号与各阶观测状态之间的偏差；－zn+1(t)/b起到前馈补偿的作用；u(t)为系统输出控制量。

ADRC控制器有响应平滑，参数适应性广，抗扰动能力强等优点，同时也会因为其TD及ESO模块通过计算逼近状态量，不能即时输出而导致滞后，应用于电机匀速扫描时其稳定性较高，但对于变速扫描[10]跟踪，滞后性会导致跟踪失准，因此本文的控制器设计中，提出以下改进：

1）用线性函数代替非线性函数[11]，有效减少可调参数，降低算法复杂度；

2）NLSEF中参考PID控制器增加积分项参与计算，以消除静差，并在参数整定时引入积分分离参数kc，将参数细化，小误差大增益，大误差小增益，防止震荡；

3）变速扫描状态下，TD环节提供的平滑过程及ESO的逼近计算导致延时跟踪的效果，因此取消TD环节，参考转速w*直接作为TD输出，同时保留ESO模块的计算方式，用实测转速w取代输出z1，状态量观测计算过程用于得到对扰动项的估测量z2，参与计算得到控制量输出。

经过以上改进的自抗扰控制器，在结构上可以描述为应用了ESO模块扰动估算方式的PID控制与前馈补偿控制的结合，它既保留了ADRC控制器对扰动观测的核心模块，能够提高电机的实时抗扰能力和稳定性，又借鉴传统PID控制根据参考量和实测量之差即时得到输出量的特点，加上前馈补偿，能实时得到变化的参考转速及实测转速的信息，减少逼近过程带来的延时。因此，改进的自抗扰控制器可以适应于PMSM根据变化的参考转速实现变速扫描控制。改进的一阶线性自抗扰控制器结构图如图2所示。

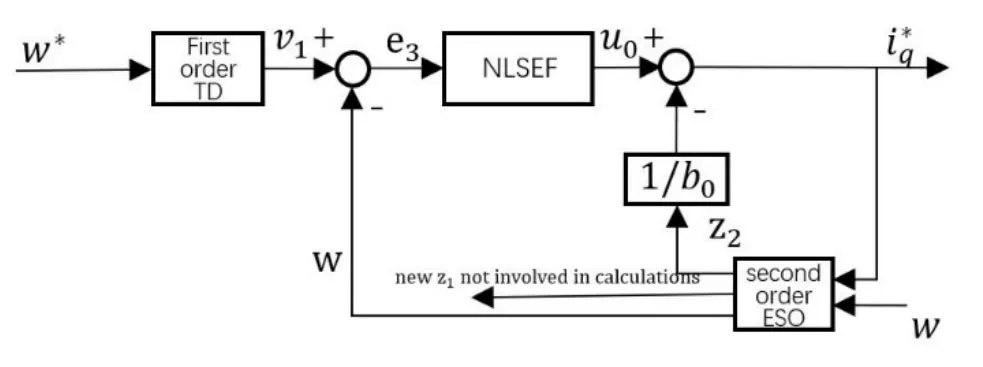
图2 改进的一阶自抗扰控制器原理图 Fig.2 Improved first-order auto disturbance controller schematic diagram

控制器完整形式如式(6)所示：

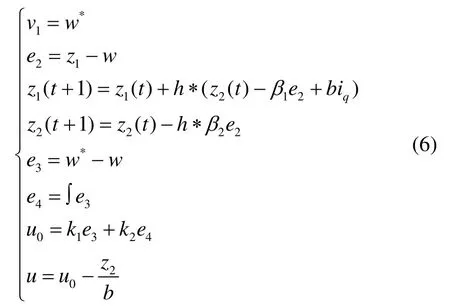
式中：w*为参考转速；v1为跟踪微分器输出；ESO根据电机输出实际转速w得到跟踪信号z1(t)及对系统扰动量的估计z2(t)；β1和β2为逼近参数；h为执行频率的倒数；为扰动补偿系数，与电机参数有关；iq为电机实测q轴电流。iq*为输出量，即电机电流环q轴参考电流；e3为跟踪微分器输出v1与电机实测转速w之差；e4为误差积分项；k1为比例系数；k2为积分系数，通过线性组合得到输出项u0；z2作为扰动项进行前馈补偿后得到控制量u，即q轴参考电流量。

2 实验方案

对于本文实验使用的某型号项目中搭载扫描镜头的永磁同步电机，工作状态下需要实现周期严格精确的慢扫快回摆扫，匀速慢扫转速7.5°/s；为保证摆扫镜头高稳定性的成像质量，要求电机零速启动响应快，稳态精度高于±2.5%。将快速回扫速度设定为正弦曲线，使电机快速回到起始位置，同时转速调整至7.5°/s继续下个周期的慢扫，因此要求其跟踪准确，超调小，抗扰能力强，相应指标为：角度定位精度高于0.005°，扫描周期时间波动小于0.005 s。

PMSM的id*＝0矢量控制选用如下方案：电流环依然采用传统PID控制，用ADRC控制器作为速度环控制。扫描电机控制流程图如图3所示。

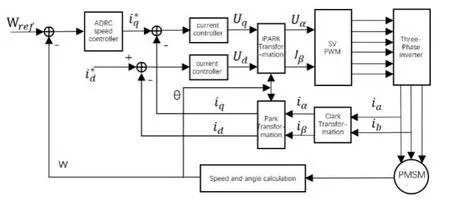
图3 伺服扫描电机控制流程图 Fig.3 Servo scanning motor flowchart

相应实验机构使用基于TMS320F2812处理器搭建的硬件电路及伺服电机摆扫机构，将设计好的ADRC控制器用于控制，评估各项性能，并与同条件下的传统PID控制器对比。实验机构及硬件电路结构如图4所示。

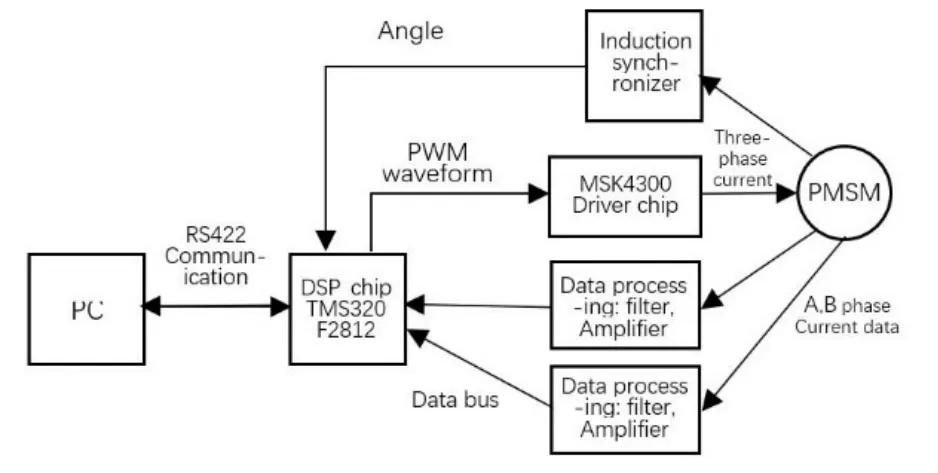
图4 实验机构原理图 Fig.4 Schematic diagram of experimental mechanism

电机选用21所永磁同步电机并搭载钛合金惯量盘，其参数如下：峰值转矩2.55 Nm，极对数6，峰值电流10 A，线电阻8.05 Ω，线电感10 mH，磁链强度0.389 Wb，永磁同步电机惯量盘及转子惯量之和0.14 kg·m2。

控制器需要调节的参数有h，β1、β2、k1、k2、kc，β1、β2为ESO收敛因子，主要决定了ESO的收敛性能；k1为比例系数；k2为积分系数；kc为积分分离参数，整定策略参考了高志强教授提出的系统带宽wc以及ESO带宽w0整定方法[12]，满足：β1＝2w0，β2＝w02。而w0、wc一般满足：w0＝3～5wc。

控制器参数的选取如下：1）速度环ADRC控制器：考虑到匀速和慢扫快回扫描测试转速不超过60°，步长h根据速度环执行频率1 kHz取h＝0.001，取ESO带宽w0＝80°/s～120°/s，有2倍裕量，实验中取100°/s，则β1＝2w0＝200，β2＝w02＝10000，比例系数k1＝100，积分系数k2＝0.0015，kc＝0.015；2）电流环PID参数：kp＝2，ki＝0.05，kd＝0；PI控制器速度环：kp＝22，ki＝0.0012，kc＝0.015。

3 实验结果及分析

3.1 匀速扫描响应及稳态精度

电机转速为零条件下，给定参考转速10°/s，待电机稳定后再使其转速增至20°/s，测得电机ADRC控制器实际转速及误差如图5(a)所示，PID控制器实测转速曲线及误差如图5(b)所示。

图5 改进ADRC控制器与PID控制器定速扫描对比 Fig.5 Comparison of improved ADRC controller and PID controller scanning on set speed

由图5得到，采用PID控制，电机零速启动至10°/s，超调9.5%，转速稳定后误差保持在±1.5%。而采用ADRC控制算法，电机从零速到10°/s，增至20°/s响应时间均为75 ms，零速启动超调为6%，变速几乎无超调，稳态误差在±1.0%范围内波动，相比于PID控制器，稳态精度提高1/3，做到了快速且超调较小的阶跃响应。

3.2 慢扫快回转速跟踪

实验中使永磁同步电机按照设定转速曲线实现慢扫快回摆扫，ADRC控制算法下的电机转速曲线及误差如下图6(a)、(b)所示，PID控制器数据如图6(c)、(d)，并局部放大。

根据图6(c)、(d)，PID控制实测转速与设定转速轨迹大致重合，转速较低时跟随性较好，7.5°/s慢速摆扫时转速误差维持在±1°/s，误差比例±1.3%，随着转速增加，跟随性变差，误差逐渐增大，曲线弧顶处出现了明显的滞后，向下偏离较严重，并出现一定的转速波动，在转速最大达到53.65°/s时，误差达到1.84°/s，误差比例3.43%，快回过渡到匀速慢扫阶段时，超调较大达到了1.31°/s。而从图6(a)、(b)改进的ADRC控制器曲线来看，实测转速曲线几乎与设定转速重合，较好地跟随了设定轨迹，在速度增至20°/s～30°/s时，开始出现了较小的滞后偏差，曲线底端出现小幅的转速波动。电机以7.5°/s慢速扫描时，误差维持在±0.06°/s，误差比例±0.8%，最大转速53.65°/s时转速出现1.85°/s波动，误差增大至3.49%，过渡至匀速慢扫时几乎无超调，很好地保证了摆扫镜匀速扫描成像的有效时间长度。

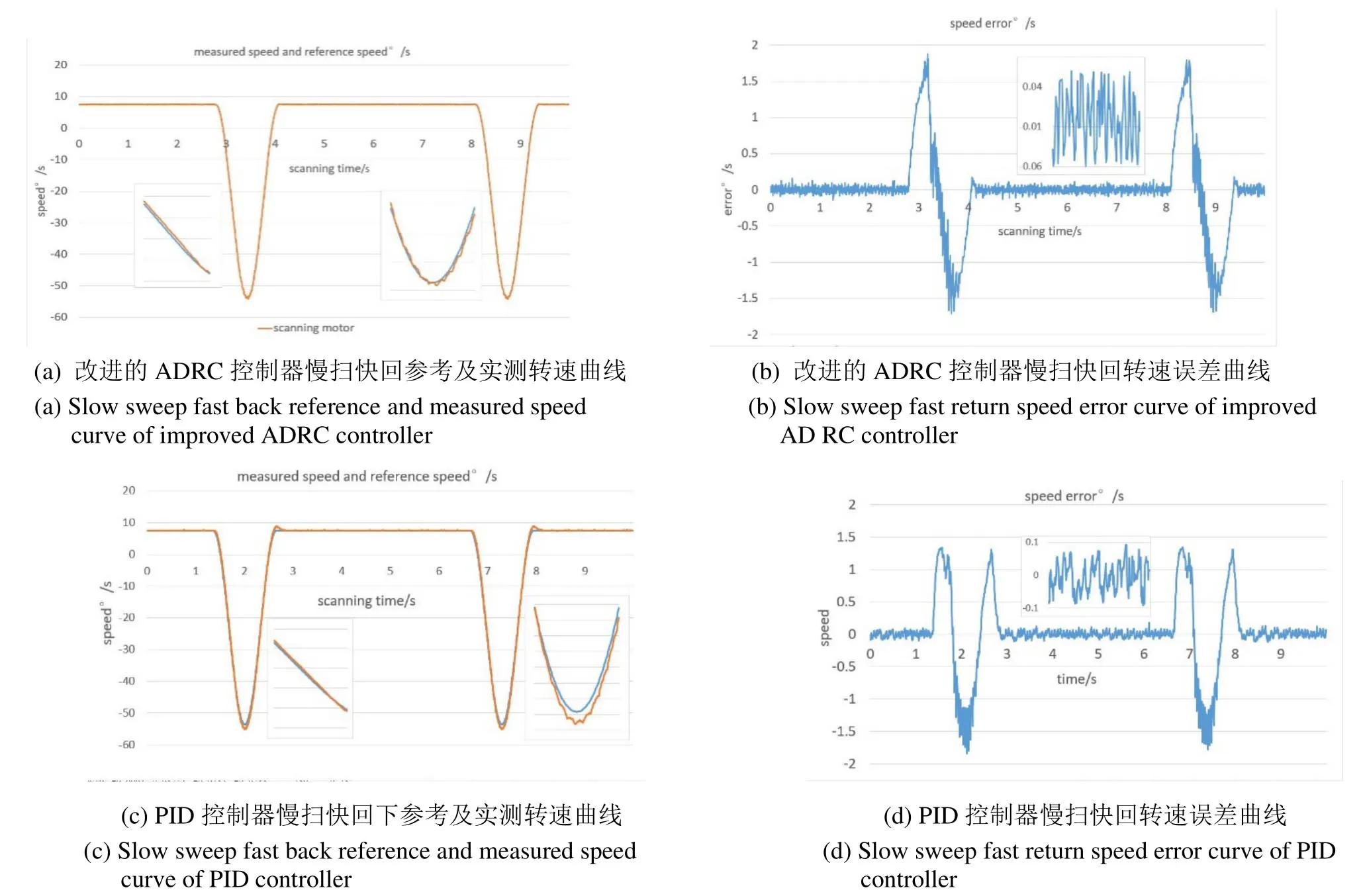
图6 ADRC与PID控制器下的电机转速曲线及误差 Fig.6 Motor speed curve and error under ADRC and PID controller

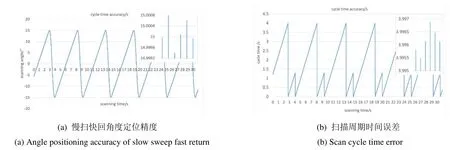
图7 ADRC控制器重复扫描角度精度及时间误差Fig.7 Angle accuracy and time error of ADRC controller on repeated scanning

测得改进的ADRC控制器重复摆扫角度定位情况如下图7(a)所示，多个周期扫描时间如图7(b)所示。从图7多个周期的慢扫快回角度定位及时间波动误差分析得到：改进的ADRC控制器角度定位误差0.0015°，周期摆扫时间最大波动0.0014 s，均在千分量级，很好地满足了指标要求，为成像机构提供了高质量的慢速摆扫时间段。

综上可以看出，相比较于传统的PID控制器，改进的ADRC控制算法能够更好地实现永磁同步电机摆扫机构的快速响应，具有更小的超调、更高的稳态精度；且针对给定的参考转速轨迹，具有更高的跟踪准确度，更好地完成了慢扫快回的转速跟踪需求。虽然在转速峰值时出现转速波动，但在长时间工作条件下，其角度重复定位精度高，摆扫周期时间波动极小，能够满足摆扫镜头匀速扫描成像过程的角度及时间精度要求，充分表现出更加优秀的控制性能。

4 结论

本文针对伺服系统中永磁同步电机变速扫描控制，提出了一种改进的自抗扰控制算法作为控制策略，并应用于某型号项目的伺服电机摆扫机构中。在满足项目指标要求的前提下，改进的自抗扰控制器在阶跃响应，稳态精度，变速跟踪速度和准确性等方面，相较于PID控制器表现出了更好的控制性能。此外，改进的自抗扰控制器一定程度上解决了控制器超调与快速响应的矛盾，增大了控制器参数的适用范围，提高了系统工作性能和其在伺服系统变速控制中的适用性，对应用于搭载摆扫镜头做变速扫描场景下的伺服机构控制器设计有一定的指导意义。