海底泵举升系统回流管道内钻井液举升效率
张 杰, 毛葛振, 李 鑫, 孙学峰
(西南石油大学石油与天然气工程学院,成都 610500)
安全泥浆密度窗口过窄是深水钻井作业一直以来所面临的一个难题[1],为了有效解决该难题,国外石油公司相继对双梯度钻井技术展开研究。从应用结果来看,目前只有挪威AGR公司所研发的无隔水管钻井液回收(riserless mud recoverg, RMR)钻井技术成功地实现了商业应用[2-4]。
海底泵举升系统是RMR技术的核心设备[5],该系统能够有效地将钻井液和钻屑通过回流管道泵送至海面钻井平台,能够有效替换传统海洋钻井技术所使用的隔水管,降低了对于海洋钻井平台建造的要求,实现了低成本、高效以及安全的深水钻井。
海底泵举升系统主要由3个部分组成,即吸入模块、海底泵和回流管道[6]。其中,回流管道作为钻井液和钻屑返出海面的唯一通道,其设计的合理性关系到整个举升系统的举升效率,也是能否有效降低深水钻井成本的关键因素。因此,有必要对海底泵举升系统回流管道的相关理论开展研究。
1 混合流体控制方程
1.1 连续性方程
回流管道内的混合流体是由深水钻井液及其所携带的钻屑颗粒组成。如图1所示,在回流管道上截取1—1和2—2两个过流断面,结合质量守恒定律以及混合流体密度的计算公式,可以得到回流管道内混合流体流动的连续性方程为
(1)
式(1)中:ρs为钻屑颗粒的密度,kg/m3;ρm为深水钻井液的密度,kg/m3;υf为混合流体的流动速度,m/s;t为混合流体流过截面所需时间,s;z为截面高度,m;CV为钻屑颗粒的体积分数。
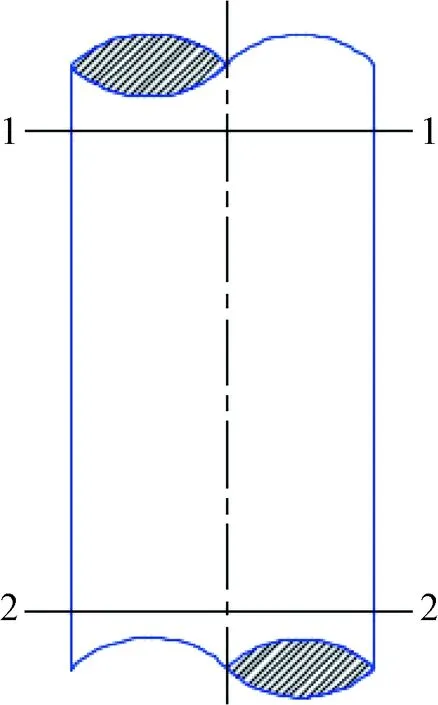
图1 回流管道截面Fig.1 Cross-sectional schematic of the return pipe
1.2 动量方程
将图1中1—1和2—2两过流断面间的混合流体视为一个系统,对该系统进行受力分析,并结合动量定理,可以得到回流管道内混合流体流动的动量方程为
(2)
式(2)中:Fn为2—2截面上单位面积混合流体所受到的由海底泵提供的推力,Pa/m2;f为单位质量混合流体的质量力,N/kg;ΔZ为1—1和2—2两截面间的标高,m。
1.3 能量方程
首先根据以下两个条件对局部能量损失的计算进行一定的简化。
(1)回流管道的长度很长,其内部所安装阀门的数量较少[7],因此可忽略由阀门所引起的局部能量损失。
(2)由于回流管道多采用刚性立管[8],其在海水环境中的方位不会发生太大的变化,因此可忽略由于管道方位变化所引起的局部损失。
结合能量守恒定律,可以得到回流管道内混合流体的能量方程为
(3)
式(3)中:Hf为2—2截面处的水头,m;Δhf为系统的扬程损失,m。
2 混合流体流态判别
深水钻井液多为合成基钻井液,该类型的钻井液通常采用幂律流体的流变模式[9]。
回流管道内混合流体雷诺数的计算公式为[10]
(4)
式(4)中:di为回流管道的内径,m;ρd为混合流体的密度,kg/m3;K为稠度系数,Pa·sn;n为流变指数,无量纲。
回流管道内混合流体临界雷诺数的计算公式为[10]
(5)
当Re (6) 式(6)中:L为回流管道的长度,m。 当Re>Rec时,回流管道内混合流体的流动为紊流流动,此时的沿程压力损失梯度为[11] (7) 式(7)中:f为摩擦阻力系数,采用牛顿迭代法对其进行迭代求解,迭代步骤为 (8) (9) (10) (11) 但是,采用临界雷诺数对回流管道内混合流体的流态进行判别的方法具有一定的局限性,因为只有当n=0.6时,计算出的沿程压力损失梯度才具有较好的连续性[12]。因此,建议将层流状态下和紊流状态下沿程压力损失梯度相同的点定义为流态发生变化的点,该方法更符合实际系统设计的需要。 混合流体的最低环空返速υα采用环空返速最小值经验公式进行计算[13]。 (12) 式(12)中:dh为井眼环空直径,m。 海底泵的最小排量[13]: (13) 式(13)中:Q为海底泵的最小排量,L/s;dp为钻杆外径,m。 回流管道内混合流体的流动速度[13]: (14) 钻屑颗粒在钻井液中的受力如图2所示。 图2 钻屑颗粒受力分析Fig.2 Force analysis chart of drilling cuttings’ particle 钻屑颗粒所受到的浮重[14]: (15) 式(15)中:ds为钻屑颗粒的当量直径,m。 实际钻屑颗粒的形状并不是规则的球形,而是呈尖锐且不规则的形状[14],通常采用三轴径方法来计算钻屑的当量直径ds,即 (16) 式(16)中:a为钻屑颗粒长轴直径,m;b、c分别为与长轴正交的两个短轴的直径,m。 钻屑颗粒所受由钻井液黏性力与压差作用所产生的总阻力[14]: (17) 当钻屑颗粒所受浮重与所受阻力相平衡时,可以得到其沉降速度: (18) 回流管道内钻井液的举升效率[15]: (19) 根据举升效率公式中所涉及的参数,分别对不同的影响因素进行分析,如图3~图7所示。 图3 回流管道内径对举升效率的影响Fig.3 Effect of the inner diameter of the return pipe on the lifting efficiency 图4 钻屑颗粒直径对举升效率的影响Fig.4 Effect of diameter of drilling cuttings’ particle on lifting efficiency 由图3可见,当泵的排量相同时,回流管道内钻井液的举升效率随着管道内径的增大而降低,且降低速率越来越快。管道的内径越大,意味着截面积越大,在泵排量相同的情况下,会导致钻井液上返速度变小,钻屑沉降速度变大,从而导致举升效率下降。需要指出的是,举升效率只是通过两种速度之间的关系所反映出来的特性,在对实际管道的内径进行设计时,还需对管道内钻屑的有效通过量进行考虑,避免钻屑在回流管道内发生堵塞。 由图4可见,当泵的排量相同时,回流管道内钻井液的举升效率随着钻屑颗粒直径的增加而降低,且降低速率越来越快。钻屑颗粒直径越大,其在钻井液中的沉降速度越大,从而导致举升效率下降。因此,在钻屑颗粒从井底进入回流管道前,应采取相应的技术手段进一步降低钻屑颗粒的直径,一方面能够提升举升效率,另一方面能够避免管道堵塞。 图5 钻屑颗粒密度对举升效率的影响Fig.5 Effect of density of drilling cuttings’ particle on lifting efficiency 图6 钻井液流变指数对举升效率的影响Fig.6 Influence of rheology index of drilling fluid on lifting efficiency 由图5可见,当泵的排量相同时,回流管道内钻井液的举升效率随着钻屑颗粒密度的增加而降低,且降低速率越来越快。钻屑颗粒密度越大,其浮重越大,从而导致其沉降速度变大,举升效率下降。因此,应采取相应的技术手段降低回流管道内钻屑颗粒的密度,进一步提高举升效率。 当泵排量相同情况下,回流管道内钻井液的举升效率随着流变指数的增加而增加。流变指数越大,钻井液的剪切应力越大,钻屑颗粒所受阻力越大,钻屑颗粒上返速度越快,因此举升效率提高。需要指出的是,并不是流变指数越高越好。从图6中可以看出,当流变指数增加到一定值时,举升效率的上升趋势不再明显,此时再进一步提高流变指数没有任何意义。因此,在对钻井液进行实际设计时,应将举升效率和成本进行综合考虑。 由图7可见,当泵的排量相同时,回流管道内钻井液的举升效率随着稠度系数的增加而增加,但当上升到一定值时,增加速率变得十分平缓。钻井液稠度系数对举升效率的影响以及对实际系统设计的指导意义与流变指数相同。 (1)通过结合由钻井液和钻屑组成的混合流体在回流管道内的流动特性,以及回流管道自身的特点,分别建立了混合流体在回流管道内流动的连续性方程、动量方程和能量方程。 (2)对混合流体在回流管道内的流态进行判别时,将层流状态下和紊流状态下沿程压力损失梯度相同的点定义为流态发生变化的点,该方法更符合实际系统设计的需要。 (3)根据回流管道内钻井液举升效率公式中所涉及到的参数,分别针对不同参数对举升效率的影响机理进行了分析,并对实际系统设计的指导意义进行了说明。
3 钻屑举升效率分析
3.1 混合流体流动速度
3.2 钻屑颗粒下滑速度
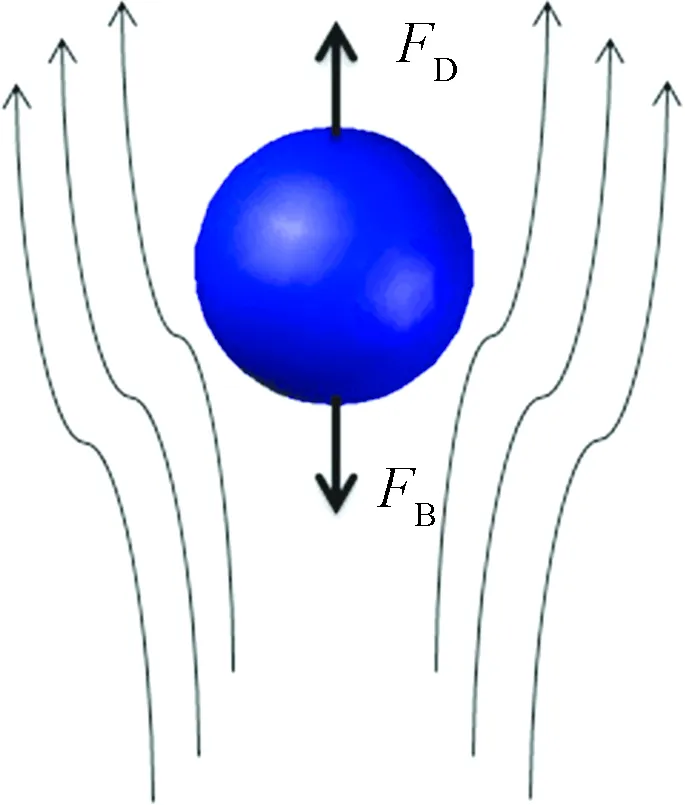
3.3 举升效率的影响因素分析




4 结论

