承插型盘扣式钢管支架盘扣节点抗扭刚度影响因素

陈桂香, 郭泽群, 胡德平, 徐 晨

(1.河南工业大学土木建筑学院， 郑州 450001；2.中铁十六局集团有限公司，北京 100018)

承插型盘扣式钢管支架以其整体性好、承载力高、拆装便捷、施工成本低等优点，在各类建设工程施工中得到应用，成为模板支架的主流架体之一[1]。承插型盘扣式钢管支架作为一种薄壁钢管结构，稳定承载力是影响其结构安全的主要因素[2]。由于连接构造原因，盘扣节点半刚性特性显著，其抗扭刚度对架体稳定承载力影响较大[3]。

为便于实际工程应用，《建筑施工临时支撑结构技术规范》(JGJ300—2013)[4]和《建筑施工承插型盘扣式钢管支架安全技术规程》(JGJ231—2010)[5]对承插型盘扣式钢管支架盘扣节点半刚性的规定均采用线性定值，抗扭刚度分别为40 kN·m/rad和86 kN·m/rad。针对承插型盘扣式钢管支架盘扣节点半刚性特性的相关研究普遍也采用线性定值，得出了35～90 kN·m/rad不等的盘扣节点抗扭刚度值[6-11]。随着节点半刚性的深入研究，相关节点抗扭试验研究和实体有限元模型数值模拟结果[8,12-13]表明：盘扣节点刚度随着节点扭矩的增加而逐渐减小，非线性明显。研究节点抗扭刚度的非线性特性，对架体稳定承载力精确数值分析和盘扣节点受力性能改进具有一定的工程应用意义。

在盘扣节点扭试验分析的基础上，应用数理统计方法，得到了盘扣节点抗扭刚度的二参数对数非线性数学模型。结合有限元分析结果，提出了便于架体结构数值分析应用的3阶段节点抗扭刚度取值，并通过架体压载试验验证了其应用于架体稳定承载力计算的合理性。结合试验现象，应用有限元数值分析手段，分析研究了各影响因素对盘扣节点抗扭刚度的作用机理及影响，可为盘扣节点构造的改良提供数值分析和试验数据支持。

1 盘扣节点抗扭试验

1.1 试验方案设计

从施工现场随机抽取6组盘扣节点构件，每组盘扣节点构件包括一根立杆和一根水平杆。在试验室对6组盘扣节点构件进行抗扭试验，构件规格及材质如表1所示。

表1 构件规格及材质Table 1 The components specification and material

注：立杆、水平杆规格为外直径(mm)×壁厚(mm)；连接盘规格为外直径(mm)×厚度(mm)；插销规格为厚度(mm)。

图1所示为盘扣节点抗扭试验。立杆长400 mm，上下两端与钢板焊接，然后在液压台上固定，两端边界条件为固接。水平杆长1 000 mm，在距离立杆轴心线1 000 mm处，采用砝码对水平杆施加竖向集中力。加载形式采用分级加载，每级加载100 N，上一级加载完成后，等位移计读数稳定后，进行下一级加载，直至构件破坏或测点位移过大超出位移计量程时停止试验。

1.2 试验计算模型

引入抗扭弹簧模型[14]模拟盘扣节点的抗扭刚度，任意受力状态下盘扣节点抗扭刚度为

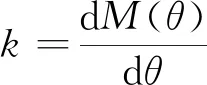
(1)

式(1)中：dθ为盘扣节点弹簧转角增量；dM(θ)为盘扣节点扭矩增量；k为盘扣节点抗扭刚度。

盘扣节点抗扭刚度是扭矩关于转角的导函数，通过盘扣节点扭矩和弹簧转角的关系曲线，可定量分析盘扣节点的抗扭刚度，定性研究抗扭刚度的影响因素。盘扣节点抗扭试验的计算模型如图2所示。

图1 盘扣节点抗扭试验Fig.1 Test on the torsional stiffness of the disk-pin joint node

图2 试验计算模型Fig.2 Model of computation for test

采用小变形假设，忽略构件变形对构件尺寸的影响。水平杆在竖向集中力荷载作用下，盘扣节点处扭矩为

M=Flh

(2)

式(2)中：lh为水平杆竖向集中力作用点至立杆轴心线的距离；F为水平杆竖向集中力；M为盘扣节点扭矩。

扭矩作用下，盘扣节点处立杆转角和盘扣节点弹簧转角分别为

(3)

(4)

式中：Iv为立杆截面惯性矩；E为钢材弹性模量；lv为立杆长度；θ为盘扣节点弹簧转角；θv为盘扣节点处立杆转角。

盘扣节点弹簧转角、盘扣节点扭矩和测点竖向位移的关系为

(5)

式(5)中：Δ为水平杆测点位移；Ih为水平杆截面惯性矩；x为水平杆测点距立杆轴心线的距离。

由式(3)～式(5)推导得盘扣节点扭矩与转角的关系为

(6)

1.3 试验数据处理

6组试验实测力-位移数据，经式(6)处理后，各组盘扣节点构件M-θ关系曲线如图3所示。

图3 M-θ关系曲线Fig.3 The relationship curve of M-θ

(7)

盘扣节点初始抗扭刚度为79.431 kN·m/rad。

图4 M-θ拟合曲线Fig.4 The fitting relationship curve of M-θ

1.4 试验分析

试验过后，6组试件中插销与连接盘接触处均出现了较大塑性变形，如图5所示；6组试件中与水平杆扣接头下翼缘接触的立杆在接触面边缘部位均有明显的塑性压痕，如图6所示。由此可知，插销与连接盘接触处和水平杆扣接头与立杆接触处的受力变形性能决定盘扣节点抗扭刚度。而影响插销与连接盘接触处和水平杆扣接头与立杆接触处的受力变形性能的因素主要包括材料弹性模量、材料应变硬化模量、插销与连接盘接触面积、水平杆扣接头与立杆接触面积。

图5 连接盘与插销破坏Fig.5 The destruction between disk plate and wedge

图6 立杆破坏Fig.6 The destruction of standing tube

2 盘扣节点抗扭有限元数值分析

2.1 有限元分析模型创建

采用有限元数值分析软件ANSYS，按盘扣节点实际尺寸创建盘扣节点三维有限元模型，对盘扣节点抗扭进行数值分析，边界条件设置与试验相同，盘扣节点三维有限元分析模型如图7所示。

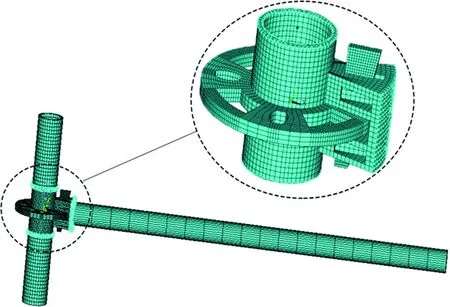
图7 有限元分析模型Fig.7 The finite element analysis model

模型中，盘扣节点处实体模型采用SOLID185单元；水平杆和立杆采用BEAM188单元；水平杆、立杆与盘扣节点采用多点约束法(multipoint constraints,MPC)进行接触连接；盘扣节点处各构件的之间的接触行为采用接触单元CONTA173和目标单元TARGE170进行模拟，接触面行为设置为标准单向接触，接触摩擦系数取0.15。

Q345材质构件屈服强度取345 N/mm2，Q235材质构件屈服强度取235 N/mm2。构件材料模型采用双线性等向强化模型(bilinear isotropic reinforcement model,BISO)，材料模型公式[16]为

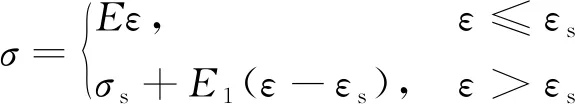
(8)

式(8)中：σ为材料应力；ε为材料应变；E为材料弹性模量，取2.06×105N/mm2；εs为材料屈服点处的材料应变；E1为材料应变硬化模量。

质量合格的钢材弹性模量几乎没有变化，而应变硬化模量的变化范围要比弹性模量大很多，平均值大约为弹性模量的1/50[17]。依据盘扣节点构造，对于给定规格的盘扣节点，水平杆扣接头与立杆的接触面积变化微小，但插销与连接盘的接触面积由于制造、安装、长时间使用等因素差异性较大。

根据材料应变硬化模量不同、插销与连接盘接触面斜率差比不同，建立5个盘扣节点三维有限元模型进行数值分析，如表2所示。插销与连接盘接触面斜率差比为

(9)

式(9)中：α为插销接触面与垂直面的夹角斜率；β为连接盘接触面与垂直面的夹角斜率；η为插销与连接盘接触面斜率差比，当η=0%时，插销与连接盘接触面积最大，当η=100%时，插销与连接盘接触面积最小。

表2 有限元分析模型分类Table 2 The category of finite element analysis model

图8 有限元分析模型曲线Fig.8 The curve of finite element analysis model

2.2 有限元数值分析结果分析

盘扣节点M-θ关系曲线的有限元数值分析结果如图8所示。依据模型1～5的曲线走势，将M-θ关系曲线分为3个阶段。第1阶段：构件基本处于弹性状态，曲线近似直线上扬；第2阶段：盘扣节点构件开始进入塑性状态后，曲线斜率先变小后增大，形成一个下凹段；第3阶段：盘扣节点构件塑形变形发展到一定程度后，扭矩增加缓慢，而转角位移迅速增加，直至达到盘扣节点抗扭承载力。

在扭矩作用下，盘扣节点处于复杂的非线性受力状态，包含材料非线性、几何非线性和接触非线性。这些非线性因素直接或间接地影响盘扣节点M-θ关系曲线走向，决定盘扣节点抗扭刚度。以模型1为例，阐述各影响因素对盘扣节点抗扭刚度的作用机理。

第1阶段：模型1在盘扣节点扭矩小于150 N·m的时候，除插销与盘扣节点连接盘接触处存在局部小范围的塑性变形外，盘扣节点各构件基本均处于弹性范围内，最大塑性应变为0.3%，如图9所示，M-θ关系曲线近似直线增长。

图9 第1阶段塑性变形Fig.9 The plastic deformation of the first stage

图10 第2阶段塑性变形Fig.10 The plastic deformation of the second stage

第2阶段：模型1在盘扣节点扭矩150～250 N·m范围内时，插销与连接盘接触处，由于接触面积小，应力集中效应明显，该处单元最大应变迅速从0.003增长到0.123，如图10(a)所示，造成此范围内M-θ关系曲线近似水平变化。扭矩为250～300 N·m范围内时，随着接触点处塑性的发展，接触面积相应增加，造成M-θ关系曲线短暂上扬，随后水平杆扣接头下缘角点出现较大塑性变形，如图10(b)所示，M-θ关系曲线又趋于水平，扭矩在300 N·m以后，盘扣节点各构件的塑性区域不断扩张，接触面积进一步增加，使M-θ关系曲线斜率有所上扬。

第3阶段：模型1在盘扣节点扭矩到达约500 N·m时，插销塑性区域贯穿整个截面，如图11所示，扭矩增加缓慢，而转角位移迅速增加，盘扣节点变成可变体系，达到极限抗扭承载力。

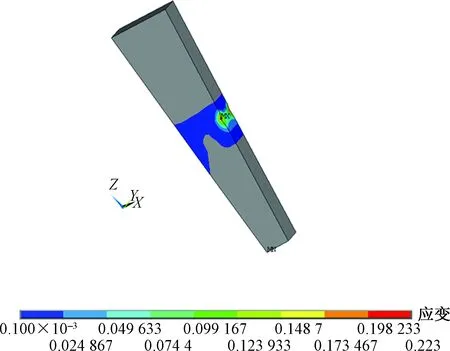
图11 第3阶段塑性变形Fig.11 The plastic deformation of the third stage

对比分析模型1～模型5的M-θ关系曲线，可得出以下结论。

(1)对比模型1～模型3，在插销与连接盘接触面积不同的情况下，第1阶段盘扣节点抗扭刚度增加了7.9%，第2阶段盘扣节点的受力变形性能得到明显改善，第3阶段曲线斜率近似一致，无明显差别，插销与连接盘接触面积对盘扣节点抗扭刚度的影响可以忽略，但极限抗扭承载力得到提高。

(2)对比模型1、模型4、模型5，在材料应变硬化模量不同的情况下，第1阶段盘扣节点抗扭刚度没有变化；第2阶段3条曲线逐渐趋于平滑，盘扣节点抗扭刚度得到较大提高。第3阶段条曲线斜率基本一致，材料应变硬化模量对盘扣节点抗扭刚度的影响可以忽略。

由上述分析知：盘扣节点扭矩在0～150 N·m范围内时，钢材弹性模量得以保证的情况下，抗扭刚度变化范围不超过7.9%。采用与试验相同的二参数非线性模型拟合模型1的M-θ关系曲线，拟合函数为

(10)

盘扣节点扭矩在大于150 N·m以后，5个模型的M-θ关系曲线虽然走向趋势相同，但在变化程度上已发生较大差异，这是插销与连接盘接触面积和材料应变硬化模量共同作用的结果。由于插销与连接盘接触面积和钢材应变硬化模量变化范围较大，后两个阶段盘扣节点抗扭刚度应视具体构件规格，依据试验数据确定。

3 抗扭刚度结果对比分析

3.1 盘扣节点抗扭刚度的影响因素

根据盘扣节点抗扭试验和有限元数值分析结果，承插型盘扣式钢管模板支架盘扣节点抗扭刚度影响因素分析如表3所示。

表3 盘扣节点抗扭刚度影响因素Table 3 The factors of torsional stiffness of disk-pin joint node

3.2 盘扣节点抗扭刚度值的确定

盘扣节点扭矩在0～150 N·m时，盘扣节点抗扭刚度的离散性较小，变化范围约8%。承插型盘扣式钢管支架结构设计中，盘扣节点构造及尺寸与表1相同，且盘扣节点扭矩不超过150 N·m时，盘扣节点抗扭刚度值建议取50～60 kN·m/rad。试验曲线与模型1曲线第1阶段初始抗扭刚度值和平均抗扭刚度值如表4所示。

表4 盘扣节点抗扭刚度Table 4 The torsional stiffness of disk-pin joint node

盘扣节点扭矩大于150～500 N·m后，插销与连接盘接触面积和材料应变硬化模量差异性较大，导致数值模拟的盘扣节点抗扭刚度离散性很大，可根据试验拟合曲线函数进行选取，建议取20～25 kN·m/rad。

盘扣节点扭矩大于500 N·m后，盘扣节点构件塑形变形严重，不适宜继续承受扭矩荷载，盘扣节点抗扭刚度建议取值为0～5 kN·m/rad。

4 抗扭刚度建议值验证

采用长柱压剪试验机，通过三级分配钢梁对承插型盘扣式支架钢管支架进行压载试验。架体构件规格、材质同节点抗扭试验，架体尺寸如图12所示。

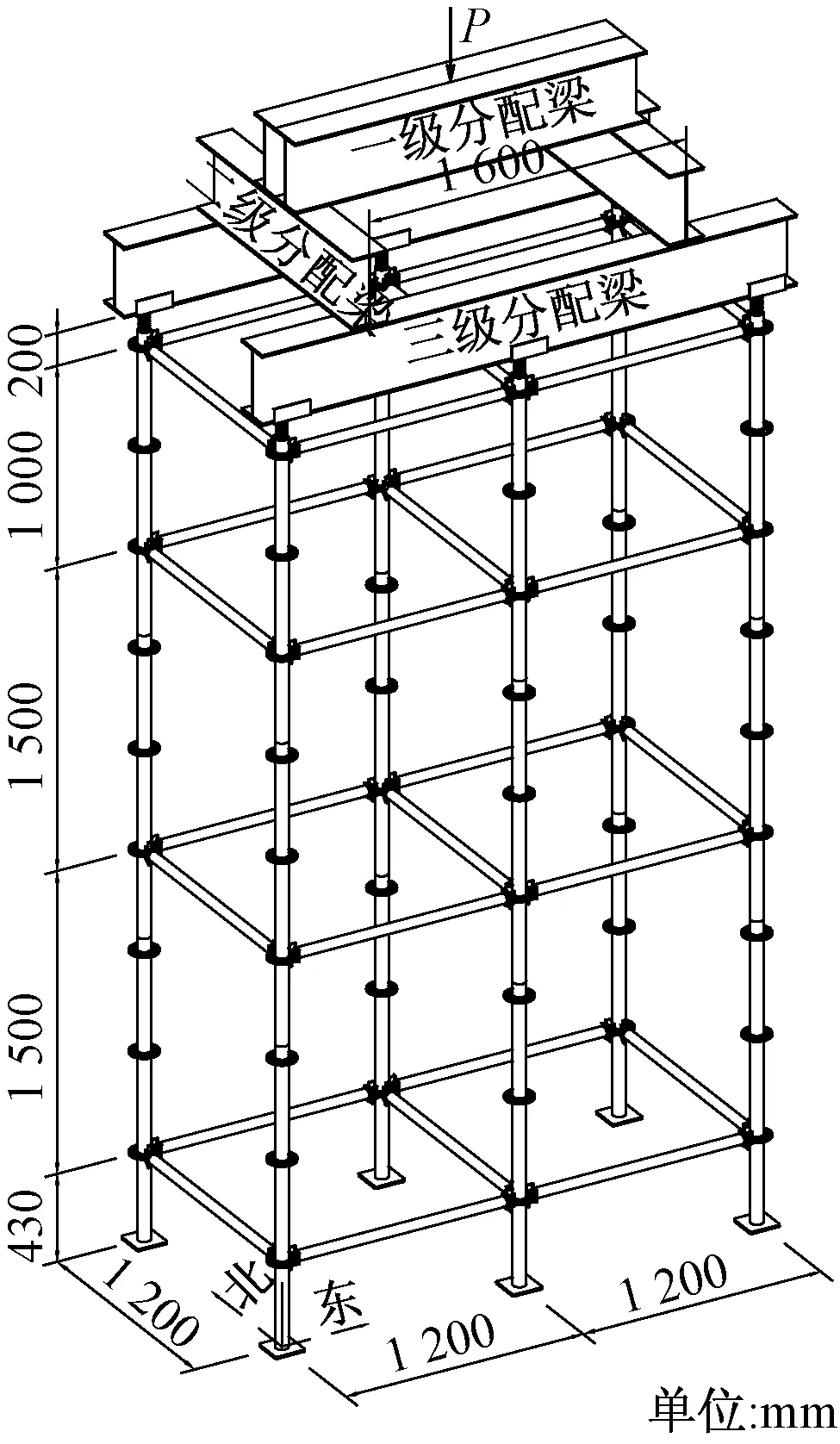
图12 试验架体Fig.12 Test frame

试验架体荷载-侧移曲线如图13所示，当荷载达到282.44 kN时试验架体失稳屈曲。

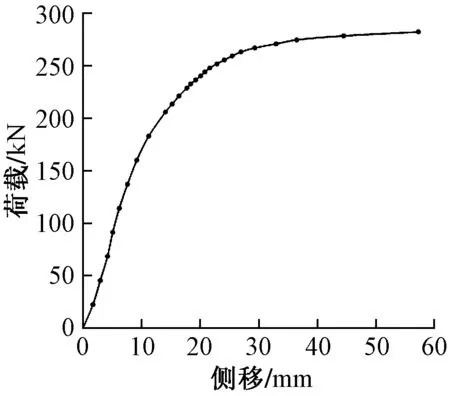
图13 试验荷载-侧移曲线Fig.13 Test load-lateral displacement curve

采用有限元软件ANSYYS创建2个试验架体有限元模型，如表5所示。立杆和水平杆采用BEAM188梁单元，按理想弹塑性处理，材料模型采用双线性等向强化模型BISO，应变硬化模量取0，材料屈服准则为Mises屈服准则。立杆屈曲强度取345 N/mm2，水平杆屈服强度取235 N/mm2。采用COMBIN39非线性弹簧单元模拟盘扣式节点处立杆和水平杆的半刚性连接。架体垂直度偏差取试验架体实测值10 mm，立杆初始弯曲取规范[5]限值1.5 mm。

依据试验架体现实边界条件，设置架体有限元模型立杆底部和顶部为铰接，对有限元模型进行非线性屈曲分析，数值分析结果与试验结果对比如表6所示。试验架体稳定承载力数值分析值与试验值误差为-1.34%～-6.9%，满足工程精度要求，且偏于安全，表明盘扣节点抗扭刚度建议值适用于实际工程。

表5 试验架体有限元模型分类Table 5 The category of the test frame FEA model

表6 稳定承载力试验值与数值分析值Table 6 The test value and the numerical analysis value of stability bearing capacity

5 结语

通过盘扣节点抗扭试验和有限元数值分析，得出了承插型盘扣式钢管支架盘扣节点抗扭刚度影响因素，其中插销与连接盘的接触面积和材料应变硬化模量影响较大。因此增大插销与连接盘的接触面积可以有效改善盘扣节点的抗扭性能。

盘扣节点抗扭刚度非线性特性明显，分为3个阶段进行选取比较合理，承插型盘扣式钢管支架各阶段的盘扣节点抗扭刚度建议值如下：盘扣节点扭矩小于150 N·m时，取50～60 kN·m/rad；盘扣节点扭矩在150～500 N·m时，取20～25 kN·m/rad；盘扣节点扭矩大于500 N·m时，取0～5 kN·m/rad。