基于改进的FP-growth算法的高校课程关联度实证研究
叶福兰
(福州外语外贸学院 理工学院, 福州 350202)
党的十八大以来,我国高度重视高等教育的发展,习近平总书记指出:“高等教育是一个国家发展水平和发展潜力的重要标志”。高等教育作为社会发展的动力之源,肩负着培养新时代社会主义事业建设者和接班人的重要使命。近些年来,我国相继出台了《教育信息化2.0行动计划》等一系列相关政策法规,将数据挖掘技术应用于教学管理中有助于提升教学管理的质量与水平。学生成绩是衡量教学质量的重要指标,然而多数研究侧重从纵向角度针对单门课程开展研究,从横向角度分析各课程之间的内在关联则少之又少。挖掘课程内在关联,合理设置课程开设学期,厘清课程前导与后续关系,优化人才培养方案,对提高学生学习效果、提升学生专业知识系统化水平具有重要意义。
1 Fp-growth算法概述
关联规则是指对给定的数据库集中的事务进行挖掘,寻找内在数据项之间的内在关系,支持度与置信度是关联规则挖掘的两个重要指标。对于形如“A=>B”的关联规则,支持度是指事务数据集中同时包含A和B的概率,如公式(1)所示;置信度是指包含A和B的事务数占包含A的事务数的百分比,如公式(2)所示。关联规则挖掘中最具代表性的算法是Apriori算法,Apriori算法是一种“产生-测试”型的关联规则挖掘算法,通过不断逐次迭代生成候选项集,结合最小支持度计数及先验原理,求出候选项集。先验原理:如果一个项集是频繁,那么它的所有非空子集也是频繁。[1]
Sup(A=>B)=P(A∪B)
(1)
(2)
FP-growth算法是基于Apriori算法基础上提出的另一种关联规则挖掘算法,旨在解决关联规则经典算法Apriori算法中存在的缺陷而提出的一种改进算法。FP-growth算法挖掘过程主要包括FP-tree构建过程以及根据FP-tree挖掘频繁模式两大步骤。FP-growth算法与Apriori算法的主要区别如下:
1)Apriori算法每生成一个候选项集均需要对数据库进行扫描;而FP-growth算法只需扫描两次数据库,第一次扫描数据集生成1-频繁项集,并按支持度计数降序原则存储于Head表中,第二次扫描数据集,将所有的项集存储于FP树中。
2)Apriori算法形成大量的候选项集;而FP-growth算法利用类似树形结构来存储数据库集中的项集信息,通过树的路径来表示事务。
FP-growth算法中频繁模式的挖掘过程是基于所构造的FP-tree,从Head表中支持度计数最小的项开始,采用分而治之的策略,通过所有的前缀路径,确定条件模式基,构造FP-tree,生成频繁项。FP-growth算法将数据库集中的事务信息压缩到FP-tree中存储,减少了扫描数据库所造成的巨大I/O开销,在空间和时间上都提高了效率。
2 FP-growth算法的改进
在应用FP-growth算法进行挖掘较大规模数据库时,所构建的FP-tree会占用大量的存储空间;同时,每生成一个频繁模式也生成了一棵FP-tree,在时间和空间上影响了算法的效率。针对FP-growth算法存在的缺点,不少人提出了改进算法。文献[2]利用邻接矩阵存储数据项的支持度计数,减少不相关的数据项,从而实现对FP-tree进行减枝;文献[3]结合挖掘目标筛选出相关的特定数据项进行分析,减少频繁模式挖掘的次数;文献[4]通过引入权重来区别数据项在事务中的重要性程度;文献[5]采用哈希头表代表FP-growth算法中的项头表,并通过合并最小支持度计数相同的节点实现压缩FP-tree;文献[6]采用有序树代替传统FP-tree并采用列表记录数据项的频繁度,从而减少存储空间及遍历FP树的次数。综上,算法的改进主要从减少不相关的数据项和只对特定相关的数据项进行频繁模式挖掘两大方面着手。
2.1 算法改进思路
针对以上提出的FP-growth算法存在的不足,本文提出了基于二维表存储事务数据的改进算法BTFP-growth。改进算法的主要原理描述如下:
1)扫描事务数据库,用二维表存储对应的所有数据项及每个事务数据,行表示数据项,列表示对应的事务,若数据项在某事务中存在,该数据项对应行所在的事务列中对应的值用1表示,否则用0表示;
2)对生成的二维表通过累加“和”的方法求各数据项的支持度计数,从而删除不满足最小支持度计数的数据项,并将二维表按照支持度计数降序排列;
3)运用逻辑“与”以及累加“和”运算求得任意两项的支持度计数,求得频繁2项集及非频繁2项集;
4)根据生成的二维表创建FP-tree;
5)结合FP-growth算法挖掘频繁项集,从项头表的最后一项开始到倒数第3项结合先验原理删除包含非频繁2项集的数据项,求包含3项以上的频繁项集。
算法的伪代码如下[7]:
Input:事务数据库D以及最小支持度阈值Minsup;
Output:所有的频繁项集。
FP-tree构造算法:
Build_FP_tree(D,Minsup,T)
1)扫描事务数据库D;
2)生成二维表,将事务数据库中的每个事务存在二维表中,行表示数据项,列表示每个事务,分别用0和1表示数据项在事务中是否出现。对二维表求每个数据项的支持度计数,删除低于最小支持度的项,并将二维表按照支持度计数调整行的顺序,生成的二维表用AT表示;
3)根据生成的二维表AT,生成频繁1项集与频繁2项集的组合,同时生成非频繁2项集;
4)创建T的根结点,根据二维表AT,调用经典FP-growth算法中的insert_tree算法生成FP树T。
改进的算法BTFP-growth(T,α):
IF (T 包含单个路径P) TEHN
FOR P中每个三项以上的结点组合β DO
产生模式β∪α,其支持度设为β中结点的最小支持度;
ELSE FOR each ai(项头表H最后一项到倒数第3项) DO
{产生模式β=ai∪α,支持度support=ai·support
构造β的条件模式基,若路径包含非频繁2项集,删除另外一个数据项,同时只选择包含3项数据项以上的路径,构建条件条件FP树Tβ
IF (Tβ≠Φ) THEN
调用BTFP-growth(T,α)}
2.2 改进算法案例分析
设有如表1某事务数据,该数据库包含9个事务,设最小支持度计数为3,改进算法挖掘事务数据库频繁项集过程如下:
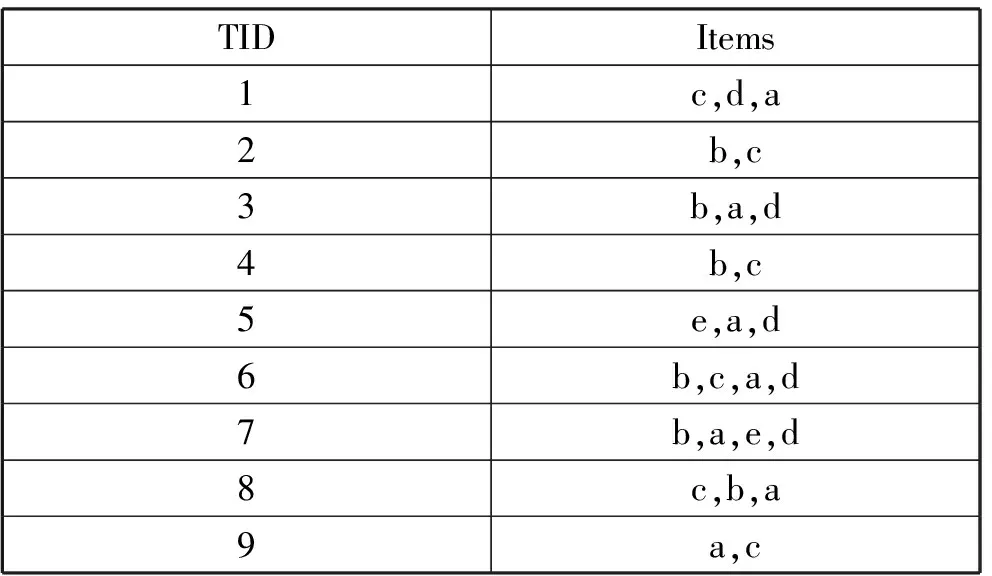
表1 事务数据
1)扫描事务数据库,生成二维表,二维表的行表示数据项,列表示某事务,1表示数据项在该事务中出现,0表示不出现,在生成的二维表中使用累加“和”求得各数据项的支持度计数分别为a:7,b:6,c:6,d:5,e:2。删除支持度计数低于最小支持度计数3的数据项e,然后将二维表按照支持度计数降序原则重新排列元组,最后生成的二维表如表2所示。
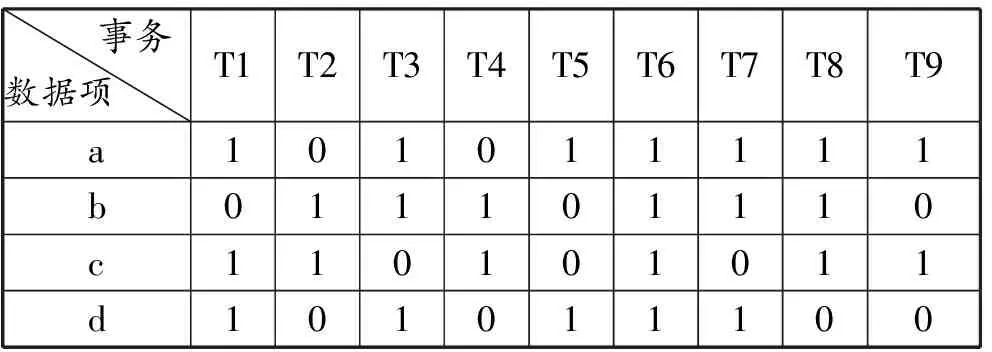
表2 事务二维表
2)根据生成的事务二维表,对任意两个数据项在同一事务中的值进行逻辑“与”运算,并将求得的逻辑“与”值进行累加,求得两个数据项的支持度计数,如数据项a与b同时出现的支持度计数为:1&&0+0&&1+1&&1+0&&1+1&&0++1&&1+1&&1+1&&1+1&&0=4。同理,求得ac,ad,bc,bd,cd的支持度计数分别为4,5,4,3,2,删除支持度小于3的cd项,求得频繁2项集为{ab,ac,ad,bc,bd},非频繁项集为{cd}。
3)根据表2的事务二维表以及所求得的支持度计数,创建FP-tree,如图1所示。

图1 FP-tree
4)从支持度最低的d项开始,向上找出3项以上的路径(因为频繁1项集合、频繁2项集已找到){a,c,d:1},{a,b,d:2},{a,b,c,d:1},得到的3项以上的集合有{a,c,d:2},{a,b,d:3},{b,c,d:1},{a,b,c,d:1},结合最小支持度计数3及非频繁2项集,得到3项以上的频繁项集为{a,b,d:3}。
5)同理,挖掘项c的频繁模式,3项以上的集合只有{a,b,c:2},不满足最小支持度计数要求。对项b和项a由于最多只得到频繁1项集或者频繁2项集,前面步骤中均已求出,因此结束频繁模式挖掘过程。
3 改进算法在高校课程关联度分析中的应用
3.1 实验环境介绍
本实验环境为Window 10操作系统的PC机,系统配置为CPU:Intet i7-7500U、内存:4G、硬盘:1T;数据的预处理采用Excel与Weka相结合;数据的实验过程采用Weka 3.8实现。Weka是新西兰怀卡大学开发的数据挖掘软件,采用JAVA语言编写,除了自身具备强大的数据预处理功能外,最重要的一个特点是该软件开源,用户可以在原算法基础上进行改进。Weka所支持的数据文件格式有:arff、csv、xls/xlsx及json等。Weka虽支持xls/xlsx格式,但需要将其转换为csv格式后才能直接打开,本文的实验数据源文件为xlsx格式,通过EXCEL基本处理后另存为csv格式。为了方便对设置各属性的类型,通过Weka打开数据源后,将其转为arff格式进行处理。
3.2 数据准备
本实验数据从学校的教务管理系统导出,数据选择某校近几届信息管理与信息系统毕业生的原始成绩作为分析的数据源,鉴于本文只研究专业课程的内在关联,故过滤不相关的字段,只保留专业基础课、限选课、任选课,由于集中性实践环节一般紧跟某门专业课而开设,在此也不考虑。针对不同年级培养方案修订导致课程差异问题,采取相似课程替换方法进行数据集成,整理后的数据如表3所示,考虑个人隐私问题,删除学号与姓名列,用序号作为关键字。
表3 学生成绩原始数据
3.3 数据预处理
1)数据清洗。从教务系统导出的数据存在缺失的情况,缺失的原因有:①学生中途转入或转出该专业,部分课程成绩缺失;②由于人才培养方案中设置了专业方向,学生修读不同方向课程,导致其他方向课程成绩缺失;③人才培养方案中设置了专业任选课,导致未选修的课程信息缺失。
针对①的情况,因数量不多,为了避免影响挖掘结果,故将该部分记录直接删除;针对②③两种情况,由于不同方向的学生或不同选修课学生所选修的课程门数均相同,所以对课程进行合并,如将《Web高级编程》与《ERP原理与应用》两门课进行合并。
2)数据离散化。受教师批改试卷标准、试卷难度等因素影响,学生的成绩分布未必成正态分布,不具可比性,若直接进行转换,则存在各课程之间不平衡问题影响挖掘结果。利用WEKA预处理功能中的Filters选项组中的无监督数值标准化方法Standardizes对成绩信息进行标准化转换,进而按比例进行离散化处理:A:5%,B:25%,C:40%,D:25%,E:5%,转换后的部分数据如表4所示。同时,将WEKA安装包中RunWeka.ini文件中的fileEncoding参数改为utf-8,使其支持中文。

表4 离散化后的数据
3.4 实验结果分析
实验过程中设置minsup=10% ,mincon=80%,执行改进的FP-growth关联规则挖掘算法BTFP-growth后,部分挖掘结果如表5所示。

表5 部分挖掘结果示例
表5中的关联规则表明前导与后续课程成绩之间的关联程度。通过所挖掘的关联规则,得到各专业课程之间的内在关联,根据学生现有成绩,分析预测后续课程成绩,对学生提出预警,教师可以根据挖掘结果因材施教。同时,教务管理人员根据关联规则设置课程开设学期,合理制定人才培养方案。
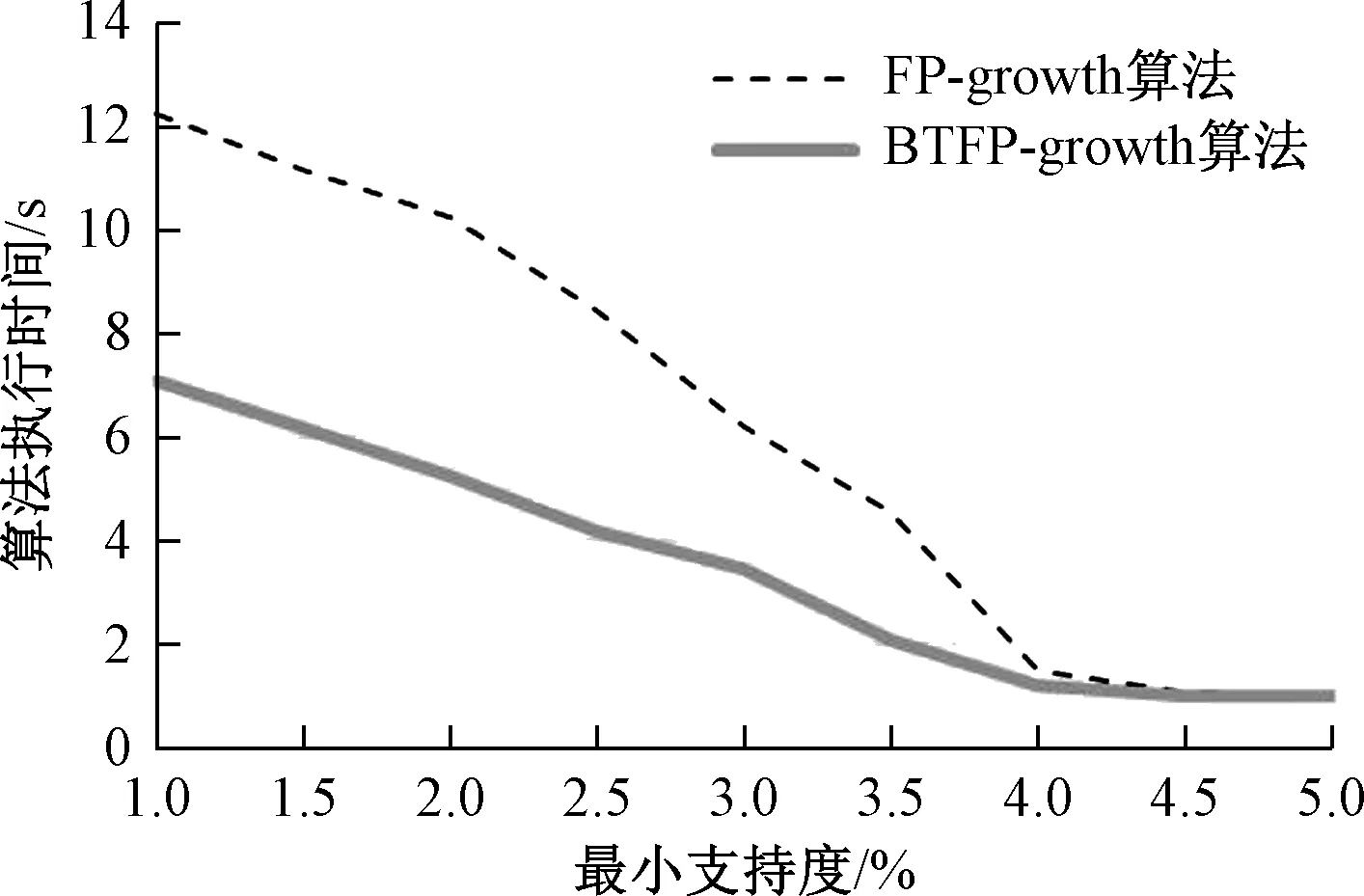
图2 算法执行效率比较
通过分别对改进前后的算法进行了实验,改进前后的算法执行效率比较情况如图2所示。实验表明当最小支持度越小,在同样的最小支持度情况下,改进的算法能过滤较多的候选项集,算法所需的时间低于传统算法,效率较高。
4 结语
本文基于二维表对传统的FP-growth算法进行了改进,提出BTFP-growth算法,减少了遍历数据库的次数,应用二维表存储事务,通过二维表计算数据项的支持度,并求出频繁1项集、频繁2项集和非频繁2项集,减少遍历FP-tree的次数,对FP-tree进行了减枝,减少了内存开销,提高了效率。结合学生成绩数据验证了改进算法的可行性,当需要分析的数据规模较大且最小支持度阈值较小时,改进算法具有较大优势。

