污秽颗粒在腕臂绝缘子表面分布规律仿真分析

张友鹏，张鼎昌，董海燕，赵珊鹏

污秽颗粒在腕臂绝缘子表面分布规律仿真分析

张友鹏，张鼎昌，董海燕，赵珊鹏

(兰州交通大学 自动化与电气工程学院，甘肃 兰州 730070)

为解决兰新高铁接触网腕臂绝缘子污闪问题，研究腕臂绝缘子表面积污规律对预防污闪事故发生、保证牵引供电系统安全运行有重要意义。以FQB-25/12型腕臂绝缘子为研究对象，利用欧拉两相流建立积污仿真模型，以污秽颗粒的体积分数为表征参数，分析颗粒浓度、风速、颗粒粒径及来流角度4种因素对绝缘子表面污秽分布的影响。研究结果表明：绝缘子表面污秽体积分数随空气中污秽浓度呈线性增长；随风速的增大，迎风面污秽体积分数迅速增大，背风面污秽体积分数增长较缓慢；随颗粒粒径增大，迎风面污秽体积分数明显增长，背风面污秽体积不断减小；来流角度在−45°到45°变化时，对于大伞裙，上表面污秽体积分数不断减小，下表面污秽体积分数不断增大，对于小伞裙，上下表面积污程度随来流角度与大伞裙相反。

腕臂绝缘子；积污规律；欧拉两相流；污秽体积分数

兰新铁路是我国第一条穿越沙漠戈壁、风灾地区的高速铁路，新疆境内地区每年春天都会出现大风沙尘雪雾天气，盐碱含量很高的污秽颗粒在绝缘子表面形成了高电导率的介质层，极易造成绝缘子大面积闪络。绝缘子污闪一般会经历积污、受潮、电弧发展和最终闪络4个阶段[1]，绝缘子表面积污分布是诱发污闪的关键因素。研究绝缘子积污规律是接触网外绝缘的基础工作，对接触网外绝缘设计、运行和维护均有重要意义[2−5]。目前，国内外学者对绝缘子积污特性展开大量研究，并通过自然积污和人工污秽试验取得丰硕成果[6−9]。自然积污试验周期长，容易受环境因素影响，结果分散性大，分析单因素影响尚有诸多困难；人工污秽试验由于成本高且与自然积污试验等价性还不完善，其结果与实际运行结果偏差较大[10]。数值模拟方法的优点是时间短、成本低、有较高准确度，可以得到单一因素对积污特性的影响。王黎明等[11]研究了支柱绝缘子积污特性，研究表明颗粒的碰撞质量随风速增大而快速增加。ZHANG等[12]研究污秽颗粒在瓷绝缘子表面的分布特性，研究表明风速对黏附颗粒的粒径分布具有显著影响。任昂等[13]针对高压直流输电线路复合绝缘子分析了颗粒粒径、风速及来流角度对粒子撞击率的影响。吕玉坤等[14]对比瓷绝缘子与复合绝缘子积污特性，认为复合绝缘子由于伞径小、伞型开放，积污程度高于瓷绝缘子。张柳等[15]研究了绝缘子不同布置方式对绝缘子污闪电压的影响，认为绝缘子布置方式影响绝缘子表面积污特性。综上所述，现有绝缘子积污研究，主要集中在不同类别输电线路绝缘子中，且绝缘子大多是竖直安装，对电气化铁路水平布置方式下的腕臂绝缘子积污特性研究较少。为此，本文选取水平布置方式的腕臂绝缘子为研究对象，采用欧拉两相流进行积污仿真研究。分析绝缘子周围流场特性，并以污秽体积分数为表征参数，研究颗粒浓度、风速、颗粒粒径及来流角度对绝缘子积污特性的影响。

1 计算流体力学仿真原理

1.1 欧拉两相流计算原理

空气中的颗粒随气流运动在绝缘子表面附近发生绕流，可以用计算流体力学中的两相流来处理，欧拉两相流模型在计算流体力学中将离散的颗粒和空气都当作连续的流体，引入体积分数来表征每一相在计算域单元中所占的体积，整个计算域中体积分数总和为1。

模型连续性方程为：

流体相的动量方程为：

固体相的动量方程为：

将绝缘子周围空气流场视为不可压缩黏性定常湍流。为适应复杂的绝缘子外形，本文采用RNG-模型进行求解，该模型在强流线弯曲、旋涡等方面有更高的精确度。RNG-模型中的方程和方程为：

1.2 模型建立及网格划分

本文选取FQB-25/12型腕臂复合绝缘子为研究对象进行仿真，绝缘子结构示意图如图1所示。绝缘子结构包含9个大伞裙、8个小伞裙，结构高度为800 mm，爬电距离为1 800 mm，大伞裙伞径为180 mm，小伞裙伞径为128 mm。

图1 绝缘子结构示意图

本文先用CAD建立绝缘子三维模型，由于不考虑污秽在金具表面分布，在三维模型中省略金具，并将三维模型导入到ICEM中进行网格划分。计算域的大小对计算结果精确度有很大影响，由于计算流体力学一般要求阻塞率不大于3%[16]，阻塞率的定义为：

式中：1为研究对象在计算域入口处的投影面积，m2；为计算域入口截面积，m2。

根据绝缘子结构可知，1=0.18 m×0.53 m= 0.095 4，本文设定的计算域入口面积为2 000 mm× 2 000 mm=4 m2。得出阻塞率为0.024。因此本文最终确定计算域尺寸为2 000 mm×2 000 mm×3 000 mm。不同部位网格划分精度不同，并且为平衡计算精度和计算资源，将计算域划分为内外2个区域，再分别对每个区域进行网格划分，计算划分区域如图2所示。在靠近绝缘子表面的区域采用四面体非结构化网格，可以很好地契合绝缘子复杂的外形，从绝缘子表面开始采用由近及远针对性划分。外层区域采用六面体结构化网格，有效的降低了网格数量，节约计算资源。四面体网格和六面体网格边界用interface进行数据交换和传递，网格数量约160万，图3为=0平面绝缘子网格划分结果。

图2 计算区域划分示意图

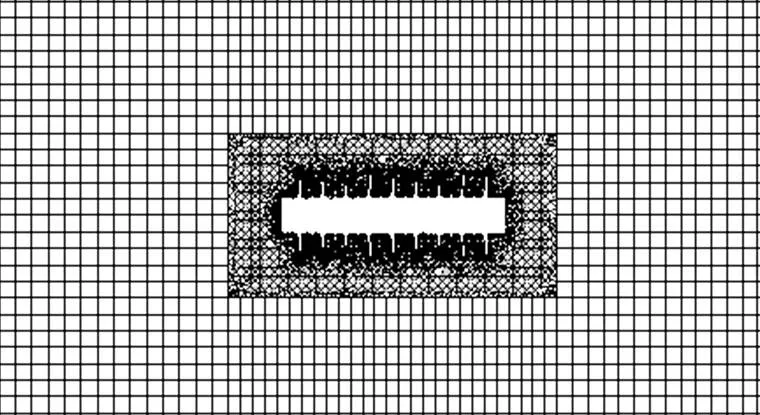
图3 x=0平面绝缘子网格划分结果

1.3 设定边界条件

将划分好的网格模型导入到CFD软件中；对模型各面设定边界条件。如图2所示，本文共设置3类边界条件：计算域左侧面定义为速度入口边界条件(velocity_inlet)；计算域右侧面定义为充分发展的出口边界(out_flow)；绝缘子表面及计算域其他4个面定义为壁面边界(wall)。入口处的湍流强度和水力直径表达式为：

式中：为计算域入口周长，m；为雷诺数。

雷诺数大小为：

式中：为流体密度，kg/m3；为流体速度，m/s；为流体的运动黏度，m2/s。

根据自然积污实验绝缘子表面污秽度粒径测量相关研究，污秽颗粒粒径在缘子表面分布为对数正态分布，粒径主要分布在15 μm左右。其中复合绝缘子表面颗粒粒径10的均值为2.90 μm，50的均值为8.25 μm，90均值为22.58 μm[17]。因此，本文设定颗粒粒分别为5，10，15，20及25 μm，颗粒选取CaCO3，颗粒密度为2 800 kg/m3。风速对绝缘子积污程度及周围流场运动特性有较大影响，西北地区铁路沿线时常出现强风、大风天气状况，风力等级在6~8级，对应风速为10~20 m/s。因此设定风速分别为1，5，10，15及20 m/s。并假设颗粒在空气中只受气体曳力和重力的作用。

为后续分析污秽颗粒在绝缘子表面分布规律，将每个伞裙划分为4个部分：迎风面、背风面、侧风面1、侧风面2，每个面所占角度均为90°[18]。伞裙部位划分如图4所示。

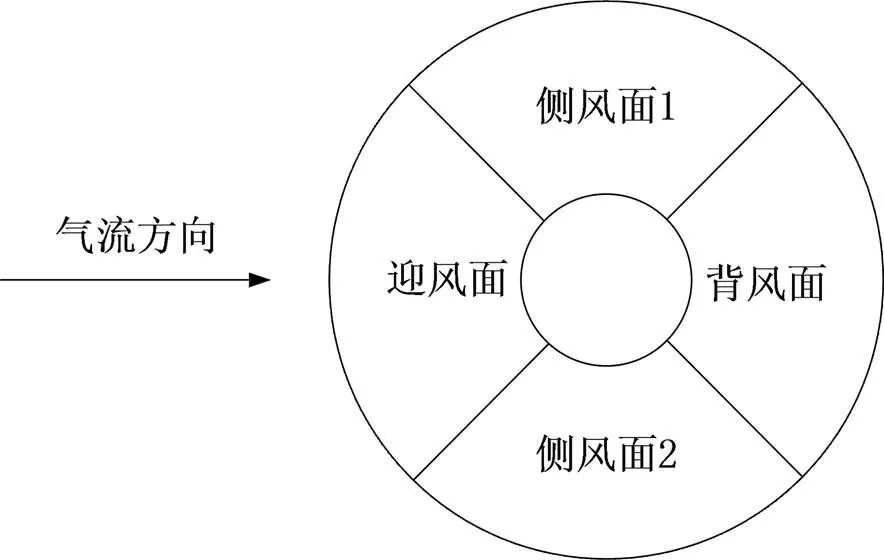
图4 伞裙部位划分

2 空气流场仿真结果

2.1 绝缘子表面静压

绝缘子表面静压反映污秽颗粒与绝缘子表面碰撞的剧烈程度。绝缘子表面静压越大，污秽颗粒与绝缘子表面碰撞越剧烈；静压越小，污秽颗粒与绝缘子表面碰撞概率越小。图5为风速为1，5，10和20 m/s时绝缘子迎风面、背风面及侧风面静压云图分布。

如图5所示，当绝缘子处于低风速下，如风速为1 m/s，绝缘子迎风面、背风面、侧风面静压数值相差很小，几乎可以忽略，说明风速较低时，绝缘子周围气流流动性较差，污秽颗粒与绝缘子表面发生碰撞的概率较低，颗粒不易附着在绝缘子表面。当绝缘子处于高风速下，如风速为20 m/s，迎风面静压远远大于背风面和侧风面静压，说明风速较高时，污秽颗粒与绝缘子迎风面碰撞更加激烈。随着风速的增大，绝缘子迎风面、背风面、侧风面静压都增大，且迎风面静压大于背风面和侧风面，不同风速下绝缘子表面静压的最大值分别为：0.78，21.2，82.5和258.2 Pa，说明风速的增大会使得绝缘子表面静压增大，从而提高污秽颗粒与绝缘子表面碰撞的概率。

2.2 绝缘子周围流场分布

污秽颗粒的运动状态与绝缘子周围流场特性有着紧密联系，流场对颗粒的受力有着一定的影响。以风速5 m/s为例，图6为=0平面速度云图分布，图7为绝缘子周围速度矢量。

当气流流过绝缘子表面时，绝缘子表面会存在明显的边界层[19]，如图6中绝缘子附近蓝色区域。在边界处的速度大小接近于0，污秽颗粒进入边界层后更容易黏附在绝缘子表面。污秽颗粒随气流的作用可以直接与迎风面发生碰撞黏附与绝缘子表面，背风面积污方式与迎风面不同，由图7中=0平面速度矢量可知，绝缘子背风面及上下表面之间有回流生成，出现局部旋涡，这使得颗粒随气流绕过迎风面以后，部分颗粒会在涡流区停留最终沉积在绝缘子背风面。由图7中=0平面的速度矢量发现，绝缘子表面边界层发生明显分离现象，边界层分离发生在背风面，分离点处形成低速涡流，因此颗粒会绕流运动到背风面，并在涡流区发生沉积。这种边界层分离现象会造成迎风面和背风面积污特性有所差异。

(a) v=1 m/s；(b) v=5 m/s；(c) v=10 m/s；(d) v=20 m/s

图6 y=0平面速度云图分布

(a) y=0平面；(b) z=0平面

3 不同因素对绝缘子积污影响

3.1 污秽颗粒在绝缘子表面分布特性分析

绝缘子积污是多种因素共同作用的结果，本文以污秽颗粒的体积分数作为表征参数，分析污秽颗粒浓度、颗粒粒径、风速及来流角度对绝缘子表面积污的影响。

式中：particle为污秽体积；air为空气体积。

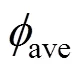
式中：A为所选取部位的面积；为离散网格节点上的污秽体积分数；Ai为微元面积；n为A上的离散数量。图8为风速为5 m/s、颗粒粒径为15 μm，空气中污秽颗粒体积分数为0.02，来流角度为0°时绝缘子积污仿真结果。图9为沿z方向上绝缘子表面污秽体积分数。

图9 绝缘子表面污秽体积分数

图8仿真结果表明，绝缘子迎风面污秽体积分数最大，其次是侧风面，背风面污秽体积分数最小；迎风面积污分布不均匀较为明显，污秽颗粒主要分布在芯棒和伞棱上。由图9可知，在不同位置处绝缘子积污分布也不均匀，污秽体积分数主要集中在0~0.15范围内，大伞裙积污程度要大于小伞裙积污程度；污秽体积分数最大值出现在沿方向0.03m处，污秽体积分数为0.45，约为空气中污秽体积分数的22.5倍。

3.2 污秽颗粒浓度对积污的影响

由于环境因素的影响，导致铁路沿线附近污秽颗粒浓度有很大差异。因此，本文对不同污秽颗粒浓度下绝缘子积污进行仿真研究(仿真条件：风速为5 m/s，颗粒粒径为15 μm，来流角度为0°)，通过调整入口处的颗粒相的体积分数模拟不同浓度下绝缘子积污状态。并以中间一组伞裙(含一大一小伞裙)进行分析。图10为不同颗粒浓度下绝缘子表面污秽分布。图11中的曲线为不同部位污秽体积分数随污秽颗粒浓度变化规律。

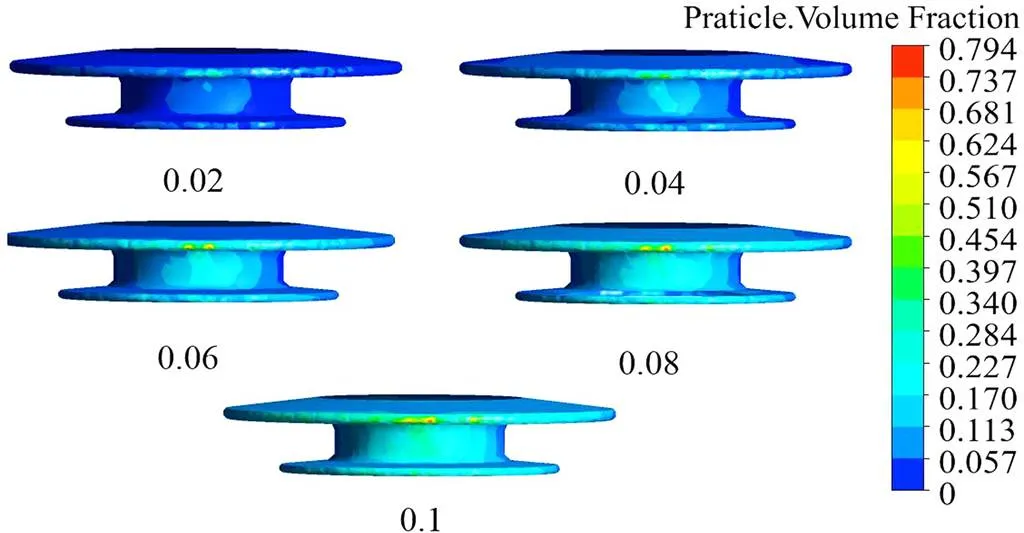
图10 不同颗粒浓度下绝缘子表面污秽分布

图11 污秽体积分数随颗粒浓度变化

如图10所示，在不同污秽浓度下，绝缘子表面污秽分布不均匀。从图11中的曲线可以看出，污秽浓度由0.02增大到0.1时，绝缘子迎风面、背风面、侧风面、都呈相同线性增长趋势。上述现象是由于随着污秽颗粒浓度的增大，单位体积空气中携带污秽颗粒个数也会增多，在气流运输作用下，更多的污秽颗粒与绝缘子表面发生碰撞，然后受到黏附力作用沉积在绝缘子表面，导致绝缘子表面污秽体积分数增大。

3.3 风速对积污的影响

风速大小对污秽颗粒的扩散及颗粒与绝缘子壁面碰撞程度起重要作用，因此风速大小对颗粒在绝缘子表面的分布有着重要影响。为研究风速对积污特性的影响，本文对不同风速下绝缘子进行积污仿真研究(仿真条件：污秽浓度为0.02，颗粒粒径为15 μm，气流倾角为0°)，并以中间一组伞裙进行分析。图12为不同风速下绝缘子表面污秽分布。图13中的曲线为不同部位污秽体积分数随风速变化规律。

图13 污秽体积分数随风速变化

如图12和图13所示，随着风速的增大，绝缘子迎风面污秽体积分数增长明显，侧风面和背风面增长趋势相比迎风面较为缓慢。这是由于随着风速的增大，绝缘子表面静压增大，污秽颗粒与绝缘子壁面碰撞程度更加剧烈，导致绝缘子表面污秽体积分数增长，迎风面静压随风速变化时总是大于背风面和侧风面，因此迎风面污秽体积分数增长较为明显，侧风面和背风面较为缓慢。

侧风面1和侧风面2污秽体积分数随风速变化趋势基本相同，但在风速为1 m/s时，侧风面1的污秽体积分数大于侧风面2，这主要是由于在风速为1 m/s时，风速对绝缘子周围流场特性影响较小，此时污秽颗粒主要靠重力沉降沉积在绝缘子表面，导致侧风面1的积污程度大于侧风面2。

3.4 颗粒粒径对积污的影响

污秽颗粒随气流在空气中运动，所受的气体曳力及自身的重力都与粒径有关。因此本文对不同颗粒粒径下绝缘子进行积污仿真研究(仿真条件：风速为5 m/s，污秽颗粒浓度为0.02，来流角度为0°)。并以中间一组伞裙进行分析，图14为不同颗粒粒径下绝缘子表面污秽分布，图15中的曲线为不同部位污秽体积分数随颗粒粒径变化规律。

图14 不同颗粒粒径下绝缘子表面污秽分布

如图14图和15所示，当污秽颗粒粒径由5 μm增大到25 μm时，绝缘子迎风面污秽体积分数由0.02增长到0.049，背风面污秽体积分数由0.018降低到0.014，侧风面污秽体积分数变化不明显，污秽体积分数基本维持在0.02左右。上述现象是由于随着污秽颗粒粒径的增大，污秽颗粒的表面积及体积都有所增大，颗粒与绝缘子接触面积增大，颗粒质量与颗粒粒径呈正相关，气流带走污秽颗粒的概率降低，颗粒与迎风面可直接发生碰撞，因此迎风面污秽体积分数随污秽颗粒粒径呈正比例增加。对于背风面积污，颗粒不能与背风面直接发生碰撞，而是绕过迎风面进入绝缘子背风面的低速涡流区再与背风面发生碰撞产生积污。污秽颗粒粒径变大，重力变大，涡流对污秽颗粒作用减弱，污秽颗粒气流跟随性变差。且此类型绝缘子伞裙倾斜角度较小，颗粒不容易停留在背风面，因此背风面污秽体积分数随颗粒粒径增大有一定下降趋势。

图15 污秽体积分数随颗粒粒径变化

3.5 来流角度对积污的影响

空气中的来流角度并不都是与绝缘子轴向垂直，当来流角度改变时，风向会严重影响绝缘子表面积污分布。因此本文选取7种来流角度：45°，30°，15°，0°，−15°，−30°和−45°。分别对7种工况下绝缘子进行积污仿真研究，并分析上下表面积污规律。(仿真条件：风速为5 m/s，污秽颗粒浓为0.02，颗粒粒径为15 μm)，取中间一组伞裙进行分析。图16为来流角度示意图，图17为不同来流角度下绝缘子表面污秽分布。图18中的曲线为不同部位污秽体积分数随来流角度变化规律。

如图17(a)，17(b)和图18所示，当来流角度从−45°到45°变化时，大伞裙上表面污秽体积分数不断减小，大伞裙下表面污秽体积分数不断增大。上述现象是由于当来流角度在−45°到0°之间，气流携带颗粒更容易与大伞裙上表面碰撞黏附，而大伞裙下表面由于上表面的阻挡，污秽颗粒与大伞裙下表面碰撞的概率减小；同理当来流角度由0°变化到45°时，污秽颗粒与大伞裙下表面更容易碰撞黏附，大伞裙上表面由于大伞裙下表面的阻挡，污秽颗粒与大伞裙上表面碰撞的概率减小。

图16 来流角度示意图

(a) 大伞裙上表面；(b) 大伞裙下表面；(c) 小伞裙上表面；(d) 小伞裙下表面

图18 污秽体积分数随来流角度变化

如图17(c)，17(d)和图18所示，当来流角度从−45到45°变化时，小伞裙上表面污秽体积分数不断增大，小伞裙下表面污秽体积分数不断减小，与大伞裙表面污秽体积分数随来流角度变化规律相反。上述现象是因为相邻2个伞裙产生涡流，污秽颗粒会在涡流中运动，使小伞裙上表面与大伞裙下表面积污程度随来流角度变化趋势相同，同理小伞裙下表面与大伞裙上表面积污程度随来流角度变化趋势相同。

4 结论

1) 污秽颗粒在绝缘子表面分布不均匀性较为明显，主要分布在绝缘子的芯棒和伞棱上，且大伞裙积污程度要大于小伞裙积污程度；随着空气中污秽颗粒浓度增大，绝缘子表面整体污秽体积分数呈线性增加。

2) 不同风速下，绝缘子迎风面静压最大，其次是背风面，侧风面静压最小；随风速的增大，绝缘子迎风面污秽体积分数明显增大，背风面和侧风面污秽体积分数增长较缓慢。

3) 随着颗粒粒径增大，迎风面污秽体积分数增大较为明显，背风面污秽体积分数不断减小，侧风面污秽体积分数变化不明显。

4) 当来流角度在−45°到45°变化时，对于大伞裙，上表面积污程度不断减小，下表面积污程度不断增大；对于小伞裙，上表面积污程度不断增大，下表面积污程度不断减小。

[1] 王晶, 李燕, 梁曦东, 等. 利用原子力显微镜探究污秽颗粒在绝缘子表面的黏附力[J]. 高电压技术, 2013, 39(6): 1352−1359. WANG Jing, LI Yan, LIANG Xidong, et al. Research of adhesion force between dust particles and insulator surface using atomic force microscope[J]. High Voltage Engineering, 2013, 39(6): 1352−1359.

[2] JIANG Z, JIANG X, GUO Y, et al. Pollution accumulation characteristics of insulators under natural rainfall[J]. IET Generation, Transmission & Distribution, 2017, 11(6): 1479−1485.

[3] 南敬, 徐涛, 万小东, 等. 人工模拟自然横风条件下绝缘子快速积污特性[J]. 中国电机工程学报, 2017, 37(11): 3323−3330. NAN Jing, XU Tao, WAN Xiaodong, et al. Fast contamination depositing characteristics of insulators under artificial horizontal wind field conditions[J]. proceedings of the CSEE, 2017(11): 3323−3330.

[4] SUN J, GAO G, ZHOU L, et al. Pollution accumulation on rail insulator in high-speed aerosol[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2013, 20(3): 731−738.

[5] ZHANG Z, LIU X, JIANG X, et al. Study on AC flashover performance for different types of porcelain and glass Insulators with Non-Uniform pollution[J]. IEEE Transactions on Power Delivery, 2013, 28(3): 1691− 1698.

[6] 巢亚锋, 高俊伟, 岳一石, 等. 湖南电网复合绝缘子带电自然积污特性[J]. 高电压技术, 2018, 44(9): 2799− 2806. CHAO Yafeng, GAO Junwei, YUE Yishi, et al. Natural pollution accumulation characteristics of composite insulators for overhead transmission lines in Hunan power grid[J]. High Voltage Engineering, 2018, 44(9): 2799−2806.

[7] WANG J, WANG K, ZHOU M, et al. The natural contamination of XP-70 insulators in Shenzhen, China[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2016, 23(1): 349−358.

[8] Ravelomanantsoa N, Farzaneh M, Chisholm W A. Laboratory investigation of the HV insulator contamination process under winter conditions[C]// International Conference on High Voltage Engineering and Application. IEEE, 2008: 116−119.

[9] 律方成, 黄华, 刘云鹏, 等. 风洞模拟自然横风条件下绝缘子带电积污特性[J]. 高电压技术, 2014, 40(5): 1281−1289. LÜ Fangcheng, HUANG Hua, LIU Yunpeng, et al. Contamination depositing characteristics of insulators under natural crosswind conditions with wind tunnel simulation[J]. High Voltage Engineering, 2014, 40(5): 1281−1289.

[10] 赵晨龙, 梅红伟, 戴罕奇, 等. 自然污秽与人工污秽绝缘子等价性分析方法研究[J]. 中国电机工程学报, 2014, 34(6): 955−964. ZHAO Chenglong, MEI Hongwei, DAI Hanqi, et al. Research on analysis method of equivalence between natural polluted insulators and artificial contaminated insulators[J]. Proceedings of the CSEE, 2014, 34(6): 955−964 .

[11] 王黎明, 刘霆, 梅红伟, 等. 基于计算流体力学的支柱绝缘子积污特性研究[J]. 高电压技术, 2015, 41(8): 2741−2749. WANG Liming, LIU Ting, MEI Hongwei, et al. Research on contamination deposition characteristics of post insulator based on computational fluid dynamics[J].High Voltage Engineering, 2015, 41(8): 2742−2749.

[12] ZHANG M, WANG R, LI L, et al. Size distribution of contamination particulate on porcelain insulators[J]. Coatings, 2018, 8(10): 339.

[13] 任昂, 毕晓甜, 秦丽伟, 等. 高压直流绝缘子积污特性数值模拟与预测[J]. 高电压技术, 2017, 43(5): 1572− 1580. REN Ang, BI Xiaotian, QIN Liwei, et al Numerical simulation and prediction on pollution accumulation characteristics of HVDC insulator[J]. High Voltage Engineering, 2017, 43(5): 1572−1580.

[14] 吕玉坤, 赵伟萍, 庞广陆, 等. 典型伞型瓷及复合绝缘子积污特性模拟研究[J]. 电工技术学报, 2018, 33(1): 209−216. LÜ Yukun, ZHAO Weiping, PANG Guanglu, et al. Simulation of contamination deposition on typical shed porcelain and composite insulators[J].Transactions of China Electrotechnical Society, 2018, 33(1): 209−216.

[15] 张柳, 巢亚锋, 黄福勇, 等. 布置方式对染污绝缘子污闪电压影响综述[J]. 中国电力, 2016, 49(6): 95−100. ZHANG Liu, CHAO Yafeng, HUANG Fuyong, et al. A review of researches on the influence of insulator on figuration on pollution flashover voltage of polluted insulator[J]. Electric Power, 2016, 49(6): 95−100.

[16] 曾锴, 汪丛军, 黄本才. 计算风工程中几个关键影响因素的分析与建议[J]. 空气动力学学报, 2007, 25(4): 504−508. ZENG Kai, WANG Congjun, HUANG Bencai. Analysis and suggestion on several key factors in wind engineering[J]. Acta Aerodynamica Sinica, 2007, 25(4): 504−508.

[17] 张燕, 苏建军, 刘辉, 等. 直流线路绝缘子自然积污污秽颗粒粒径分布特征[J]. 高电压技术, 2017, 43(9): 2935−2942. ZHANG Yan, SU Jianjun, LIU Hui, et al Particle size distribution characteristics of naturally polluted insulators in service of HVDC transmission line[J]. High Voltage Engineering, 2017, 43(9): 2935−2942.

[18] 唐秋明. 高压绝缘子表面积污及电场分布的研究[D]. 苏州: 苏州大学, 2017. TANG Qiuming. Contamination characteristics and electric field distribution of high voltage insulators[D]. Suzhou: Soochow University, 2017.

[19] 蒋兴良, 李海波. 计算流体力学在绝缘子积污特性分析中的应用[J]. 高电压技术, 2010, 36(2): 329−334. JIANG Xingliang, LI Haibo. Application of computational fluid dynamics to analysis of contamination depositing characteristics of insulators[J]. High Voltage Engineering, 2010, 36(2): 329−334.

Simulation analysis on distribution rules of contamination particles on the surface of cantilever insulator

ZHANG Youpeng, ZHANG Dingchang, DONG Haiyan, ZHAO Shanpeng

(School of Automatic & Electrical Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)

In order to solve the problem of catenary cantilever insulator pollution flashover in Lanzhou-Xinjiang high speed railway, it is important to study on accumulated contamination rules of catenary cantilever insulator to ensure the stable operation of traction power supply system. In this paper, the cantilever insulator FQB-25/12 was taken as the research object. Euler two-phase flow was used to establish a simulation model of insulator contamination, And then, the contamination volume fraction was taken as characteristic parameter, through which the influences of particle concentration, wind velocity, particle size and angle of air flow on the distribution of contamination on insulator surface were figured out. The research results show that for particle concentration, the volume fraction of contamination particles grows linearly with the contamination concentration in the air. For wind velocity, the higher the wind velocity is, the faster the volume fraction of contamination particles at windward grow, while the slower at leeward. For particle size, with larger size of the particle, the volume fraction of contamination particles on the upper surface of the shed increases obviously, while on the lower surface decreases continuously. And in terms of angle of air flow, when it varies from −45° to 45°, for big sheds, the volume fraction of contamination particles on the upper surface of the shed decreases, while on the lower surface increases. And for small sheds, the rules are the opposite.

cantilever insulator; contamination rules; Euler two-phase flow; contamination volume fraction

U225.8

A

1672 − 7029(2020)04 − 1015 − 10

10.19713/j.cnki.43−1423/u.T20190636

2019−07−15

国家自然科学基金资助项目(51567014，51767014，51867013)

赵珊鹏(1983−)，男，吉林敦化人，副教授，从事高电压与外绝缘技术研究；E−mail：zsp@mail.lzjtu.cn

(编辑 蒋学东)