基于贝叶斯更新的盾构掘进经验模型可靠性分析
吴波,邓政,黄惟,李志刚,张子仪
基于贝叶斯更新的盾构掘进经验模型可靠性分析
吴波1,邓政1,黄惟1,李志刚2,张子仪1
(1. 广西大学 土木建筑工程学院 工程防灾与结构安全教育部重点实验室,广西 南宁 530004;2. 中国水利水电第一工程局有限公司,吉林 长春 130062)
利用一种能够考虑经验模型不确定性的贝叶斯更新方法,将模型偏差系数视为随机变量,并根据现场观测数据对其进行不断更新,所得更新结果可用于后续阶段盾构掘进最大地表沉降和失效概率的预测。以福州地铁某区间隧道掘进为例,将本文所提方法应用于Peck模型、O′Reilly-New模型和刘建航修正的Peck模型等3种经验模型。研究结果表明:3种模型一般都会高估最大地表沉降,其中 Peck模型偏差最大,刘建航修正的Peck模型次之,O′Reilly-New模型最小,而刘建航修正的Peck模型偏差比O′Reilly-New模型的变异性更小,通过所提方法可以有效考虑模型不确定性的影响;盾构掘进过程中,与另外2个模型比较,利用刘建航修正的Peck模型进行计算得到的结果更加准确;在本文所研究的算例中,盾构掘进过程中,检测数据不断增加,降低了模型偏差系数和土体参数的波动概率,从而使隧道失效概率的预测值降低。
盾构隧道;最大地表沉降;贝叶斯更新;失效概率;监测数据

在盾构隧道掘进过程中,会使周边地表产生一定程度的沉降。地表沉降过大时,会对周围建筑物和生态环境造成破坏。所以,在盾构隧道掘进过程中,最为核心的问题是预估地表的沉降与失效概率[1−2]。在预测地表沉降方面有很多方法,如:数值分析法[3−4]、经验公式法[5−6]和模型试验法[7−8],其中经验公式法因其高效性和便利性而在工程实际中得到了广泛的应用。Peck[5]研究分析了大量的地表沉降数据,提出了地表沉降槽正态分布的特征和地层损失的理论,并于1969年率先总结出了地层损失理论以及预估地表沉降的方法;依据真实的地表沉降数据,竹山乔利用回归曲线预测最大地表沉降公式;Attewell[6]等也提出了地表沉降槽呈现正态分布的概念,并通过计算得到了沉降槽的宽度系数。经验公式需要以大量施工实测数据为前提,在回归分析基础上确定拟合公式,所得结果可大体反映本地区地表移动的客观规律。盾构掘进期间的地表沉降情况可通过这些经验模型进行预测,但是利用经验公式进行估算时往往难以考虑地层详细条件,且相应的施工条件、管片刚度等无法完全考虑,所以经验公式所得结果和实际情况存在一定偏差。在一定的地层件条件下确定出的经验公式因其只能单纯的应用在相同或相似的地层条件下所得结果才可以满足应用要求,所以其适用性不高。除此之外,经验公式还有一个缺点就是一些物理参数无法精确定义,所以无法广泛推广应用。现有资料中,在定义模型误差时一般使用偏差系数,根据这个结论,怎样有效地估算模型不确定性有重要的意义。此外土体有一定的空间变异性,其性质和所处位置密切相关。地铁隧道掘进是一个持续性的过程,通过现有技术能够很方便地获取不同施工时期的地表沉降数据,利用这些数据进行模型偏差系数的反演,从而能更好地满足工程应用要求。同时应用各环节土体参数与模型偏差系数,能够更精确地预估隧道后续掘进的响应,也可以更合理地估计失效概率。本文在研究过程中应用贝叶斯更新方法,基于这种方法并结合盾构掘进实测数据来更新模型偏差系数和土体参数。与QI等[9]不一样,使用本文的方法可以直接获得模型偏差系数样本,进而更有效地预估和更新掘进响应与失效概率。以福州地铁某区间盾构隧道掘进为例,利用Peck,O′Reilly-New与刘建航模型对隧道地表沉降预测进行比较分析,进而对本文使用的预测方法的有效性进行了验证。
1 盾构隧道掘进的地表沉降经验模型
1.1 Peck模型
Peck[5]较早研究了隧道施工相关的地面沉降问题,且通过相关数学方法对隧道开挖地表沉降实测数据进行了分析,在1969年率先总结了地层损失理论以及预估地表沉降的方法,即沿用至今的Peck公式。此后,通过科研人员不断的深入研究,此公式在隧道施工地表沉降预测方面得到了广泛应用。假定在不排水条件下,沉降槽体积与地层损失体积一致;隧道长度轴向的地层损失表现出均匀分布特征,横向的沉降近正态分布。依据该假定可得地表沉降横向分布的预测计算表达式:




式中:为覆土厚度;为计算半径;为隧道周围地层内摩擦角。
1.2 O′Reilly-New模型
O′Reilly等[11−13]根据Peck提出沉降槽正态分布的概念,对英国地铁隧道施工时沉降槽宽度、最大沉降量和沉降槽体积等基础数据进行研究分析,通过实际研究得出:无论施工环境土体性质是黏土还是砂土,隧道直径对地表沉降槽的影响不大,且地表沉降槽的宽度和隧道埋深有相互联系。经过统计分析19例黏性土、砂性土和16例回填土地质工况隧道基础上,总结出了沉降槽宽度与隧道埋深深度的关系,如式(4)所示:
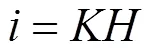
其中:是统计系数,它跟土的性质有关,即土的性质不同,得到的值也不相同。砂土和黏土中,值的范围分别取0.2~0.3和0.4~0.7。
1.3 刘建航模型
在Peck的基础上,刘建航等[14]在纵向沉降方面对上海地铁进行了研究,通过统计发现地铁隧道沉降的一般规律,并且在此基础上提出了“负地层损失”理论,并根据相关参数得到了预测地铁隧道纵向地表沉降的数学表达式:


2 考虑模型不确定性的贝叶斯更新
Peck模型的缺陷表现为没有考虑到模型偏差,而刘建航引入了偏差系数,但在实际估算时,通常将该系数设为常量。为了提高模型估算的精确度,本文将偏差系数设为一个随机变量,并且该变量随隧道掘进而不断更新。
本节选择刘建航修正的Peck模型,以最大的地表沉降为监测信息,用贝叶斯方法对偏差和土体参数进行迭代更新,因Peck和O′Reilly-New模型的缺陷,因此本文对其更新的对象只有一个,即偏差系数。
2.1 贝叶斯框架
本文以乘积的形式考虑模型偏差系数,即

如果使用的模型偏差系数呈现正态分布,并且均值和标准差分别为和。根据相关概率计算公式[15−17],在监测数值一定的条件下,对于参数和来说,它们的后验联合概率密度函数计算公式如下所示:
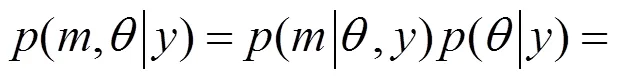

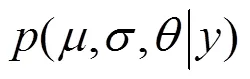

IPG PHOTONICS是IPG在中国投资建成的全资子公司,主要负责IPG光纤激光产品在中国地区的市场开拓、应用研发、系统集成及产品销售。IPG是全球最大的光纤激光研发中心,其生产的高效光纤激光器、光纤放大器以及拉曼激光技术均走在世界的前端,并被各国广泛用于材料加工、测量、科研、通信及医疗等领域。

式(9)为贝叶斯更新方程,该方程考虑了模型的不确定性因素。
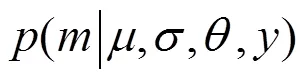


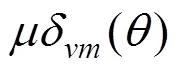

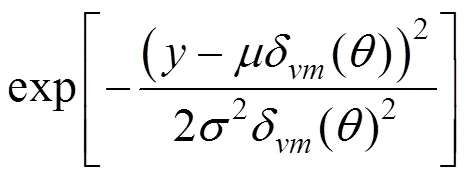
联合式(9)~(11),能够知道与服从后验分布。使用贝叶斯进行参数更新[18],并且将施工时得到的实际测量信息当作一个整体,然后更新中间环节参数。进一步,使用MCMCS[19]按照式(9)能够得到大量与的数据,通过这些数据可以对失效概率进行更新操作。
2.2 失效概率的更新
在对失效概率进行更新操作时,监测的对象为最大地表沉降,并根据观测到的信息判断盾构的好与坏。由于观测信息运用于更新其他参数,则更新之后的失效概率表示为:


3 某地铁区间隧道案例分析
3.1 工程概况
以福州地铁某区间右线隧道掘进为例,比较Peck模型、O′Reilly-New模型和刘建航修正的Peck模型3种经验模型,在考虑模型不确定性的贝叶斯更新框架下其最大地表沉降和失效概率的更新和预测结果。区间右线隧道长920.93 m(起点里程SK29+939.853,终点里程SK30+860.781),采用土压平衡盾构机掘进,共分为765环掘进,以每100环为一个阶段,在第3至6阶段隧道最大地表沉降观测值较大,使用这些值进行更新能够获得较为明显的效果,因此本文仅对阶段3~6进行贝叶斯更新。隧道主要穿越(含泥)中细沙、粉细砂地层,区间纵坡形态为V型,埋深7.2~13.7 m(埋深最深处在SK30+397.917),埋深最大处在掘进时间为166 d。图1为隧道土层纵断面图,图2为掘进过程中各个阶段的地表沉降最大观察结果。

图1 隧道土层断面

图2 隧道最大地表沉降观测值

本文在研究过程中通过贝叶斯整体更新法并基于5万个样本的MCMCS更新参数。详细操作如下:完成第3阶段之后,利用该时期的观测数据与式(9)对模型的参数进行更新;完成第4阶段后,利用前面3和4共2个阶段的观测数据再次对模型的参数进行更新的操作;依次循环进行。除此之外,本文也对最大地表沉降和失效概率分别进行了预测和更新,其中更新的操作对应的是当前正在进行的阶段,而预测对应的是后面要施工的所有阶段。比如:完成3阶段的更新工作之后,需要进行2个操作,其一是利用目前的参数值对现阶段的最大地表沉降与失效概率进行更新的,其二是结合后续即将施工的4~6阶段的信息,对各个时期的上述2个重要参数进行预测,依次循环进行。
3.2 模型不确定性的更新
利用贝叶斯进行更新,在不同施工阶段中利用3种不同经验模型的模型偏差系数更新所得结果如图3,具体分析此图结果可知,这3种模型结果和实测值都存在偏差,预测的最大地表沉降都高于实际值。对比可知,Peck模型偏差最大,O'Reilly-New模型次之,刘建航修正的Peck模型最小。O'Reilly- New模型与刘建航修正的Peck模型进行比较,后者的偏差变异性较小(即更小),也就是说,刘建航修正的Peck模型的计算结果比较稳定。此外,在盾构机不断推进时,施工过程中监测信息数据量增大,模型中的不确定性随之减小,本文所运用的方法也可对此进行描述。以刘建航修正的Peck模型进行举例分析,第3阶段选只有一个监测数据更新操作,这种条件下模型偏差系数的为0.39;同样条件下到第5 阶段,通过3个数据进行更新,则此系数为0.31,其后基本保持恒定直到第6阶段。
3.3 最大地表沉降和失效概率的更新
在模型偏差系数和土体参数(仅对刘建航修正的Peck模型来说)更新的基础上,图4得到3种经验模型的贝叶斯更新数据。具体分析图3结果可知,在图3(a)中,更新数据越靠近1:1的线,说明这与观测值越靠近,即数据越精确。为了进行比较,图4(a)给出没引入偏差系数的结果。对Peck和O′Reilly-New模型,进行估计过程中,不考虑偏差系数会导致最大地表沉降估计值高于实测值,但是和其他2个模型对比,O′Reilly-New模型估计值和测量值的差异更小,精度更高,这和上节中对模型偏差系数所得结果相一致。考虑模型偏差系数的同时,应用贝叶斯方法进行更新,则所得的最大地表沉降估计结果和观测结果是一致的,这就证明本文使用的方法是有效的。

(a) 后验分布;(b) 均值和标准差

(a) 最大地表沉降;(b) 失效概率
考虑模型不确定性后,Peck模型所得估计结果也高于测量值观测值。其原因为此模型是基于20世纪70年代前的开挖案例进行回归而建立的,当时盾构掘进方式和管片强度等因素与现今存在较大差异,掘进引起的地表沉降较大,故该方法应用于此区间右线隧道时结果会偏大。O′Reilly-New模型的更新结果最接近实测值。虽然O′Reilly-New模型只考虑了埋深的影响,但它是根据英国多个不同土层地铁隧道案例提出来的,考虑了砂性土对地表沉降的影响,故对此区间右线隧道有较好的适用性。刘建航修正的Peck模型的更新结果在5个阶段和观测值都很接近,在持续的掘进过程中,该模型的估计精度在不断提高。这种模型在分析过程中综合考虑了开挖深度及部分土体参数相关因素的影响,和实际情况更接近,可更好地满足工程应用要求,因而可有效进行隧道最大地表沉降的预测分析,且它是根据上海地区的盾构掘进案例而提出,而上海与福州均处于中国东部沿海地区,土体性质会有一定的相似性。
在图4(b)中可以看到上述3个模型的失效概率更新情况。与O′Reilly-New以及刘建航修正的Peck模型相比,Peck模型对应的失效概率值明显偏大,O′Reilly-New和刘建航修正的Peck模型的失效概率值相差非常小,且3种模型的失效概率都会伴随盾构掘进而减小。其中,O′Reilly-New模型和刘建航修正的Peck模型的失效概率分别稳定在7%和5%左右,考虑到盾构掘进后2次注浆及地层应力调整,在盾构隧道施工阶段失效概率可以接受。当模型的监测信息数据量提高时,偏差系数和土体参数在不确定性方面会有所减小,进而使得失效概率值减小。出现这种现象和实际施工条件是相吻合的,通过本文提出的方法可以有效考虑这种情况。
3.4 最大地表沉降和失效概率的预测
当处于不同的掘进阶段时,使用贝叶斯方法可以对其最大的地表沉降与失效概率进行预测分析。对比分析可知图5(a)中的Peck模型预测所得最大地表沉降预测结果偏差较大,但是,随着进一步的掘进,其结果会趋于观测值。比如:当处于阶段3对第6阶段进行预测时,其预测结果是实际值的2倍,为14.61 mm,而在第5阶段对第6阶段进行预测时,预测结果为10.10 mm,预测的精度显著的提高。O′Reilly-New模型和刘建航修正的Peck模型的所得结果和实测值一致性更高。其中,刘建航修正的Peck模型预测精度在掘进持续过程中不断提高。
相同地,在失效概率预测上,Peck模型的结果较大,而O′Reilly-New模型与刘建航修正的Peck模型预测结果与实际接近,3个模型所预测的失效概率均随着开挖的进行不断减小。其中,在图5(b)与图4(b)上的趋势相同,但是对于图4(b)而言,其失效概率在同一阶段更大,导致该现象的原因是其在进行预测时,可用数据较少。进行分析时,在阶段4,对失效概率进行更新过程中,需要用到3和4共2个阶段实测值。对失效概率进行预测时,单纯用到第3阶段数据,因而阶段4预测时的失效概率(如刘建航修正的Peck模型的12.6%)会高于更新后的失效概率9.1%。除此之外,由图5(b)可知,在O′Reilly-New模型与Peck模型中,其失效概率预测值在后续的所有阶段中保持不变。这是由于它们仅仅考虑了开挖深度对地表沉降的影响,它们的失效概率只与偏差系数有关,当对偏差系数进行更新之后,后面的失效概率值维持恒定。从这个方面分析可知,刘建航修正的Peck模型比Peck模型和O’Reilly-New模型更优。

(a) 最大地表沉降;(b) 失效概率
4 结论
1) 基于经验模型进行贝叶斯更新过程中,假设模型偏差系数为一个随机变量,和掘进过程密切相关,则更新后的结果和实测值更接近。
2) 和实测值相比,3种经验模型计算结果都存在偏差,估计所得最大地表沉降值都高于实际值。在这3种模型中,按照偏差从大到小排序依次为Peck模型、刘建航修正的Peck模型和O′Reilly-New模型。在变异性方面,刘建航修正的Peck模型比较小于O′Reilly-New模型。
3) 在预测和计算最大地表沉降与失效概率方面,Peck模型表现不是很好,偏差较大。后2个模型在这方面的表现相近。当隧道掘进不断推进时,刘建航修正的Peck模型更有优势。
4) 随着隧道不断掘进,由这3种模型计算的失效概率都会不断减小,主要原因在于施工中监测所得的数据增加后,模型参数的不确定性降低。这个情况与实际相吻合,因此,本文所采用的方法可以有效考虑这种情况所产生的影响,为盾构隧道掘进最大地表沉降和失效概率的预测提供参考。
[1] 刘宝深. 急待深入研究的地铁建设中的岩土力学课题[J]. 铁道建筑技术, 2000(3): l−3. LIU Baoshen. Problems on geomechanics in need of immediate deep research in subway construction[J]. Railway Construction Technology, 2000(3): l−3.
[2] ZHANG Z G, HUANG M S, ZHANG M X. Theoretical prediction of ground movements induced by tunnelling in multi-layered soils[J]. Tunnelling and Underground Space Technology Incorporating Trenchless Technology Research, 2010, 26(2): 345−355.
[3] Loganashan N, Poulos G H. Analytical prediction for tunnel induced ground movements in clays[J]. Journal of Geotechnical and Geoenvironmental Enginnering, 1998, 124(9): 846−856.
[4] 陈先国, 高波. 地铁近距离平行隧道有限元数值模拟[J]. 岩石力学与工程学报, 2002, 21(9): 1330−1334. CHEN Xianguo, GAO Bo. 2D fem numerical simulation for closely-spaced parallel tunnels in metro[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(9): 1330−1334.
[5] Peck R B. Deep excavation and tunneling in soft ground[C]// 7th International Conference on Soil Mechanics and Foundation Engineering. Mexico City: International Society for Soil Mechanics and Foundation Engineering, 1969: 225−290.
[6] Attewell P B, Farmer I W. Ground deformations resulting from shield tunnelling in London clay[J]. Canadian Geotechnical Journal, 1974, 11(3): 380−395.
[7] Shinichir I, Toshiyuki H, Kenji M, et al. Settlement through above a model shield observed in a centrifuge[C]// Centrifuge 98. Tokyo, 1998: 713−719.
[8] FANG Y, CHEN Z T, TAO L M, et al.Model tests on longitudinal surface settlement caused by shield tunnelling in sandy soil[J].Sustainable Cities and Society, 2019 (47): 501−504.
[9] QI X H, ZHOU W H. An efficient probabilistic back-analysis method for braced excavations using wall deflection data at multiple points[J]. Computers and Geotechnics, 2017(85): 186−198.
[10] 吴波. 浅埋暗挖法地铁施工沉降控制基准分析及应用[J]. 世界隧道(增): 2000: 241−244. WU Bo. Analysis and application of settlement control criteria for metro excavation by shallow mining method[J]. Modern Tunnelling Technology (Suppl), 2000: 241−244.
[11] O'Reilly M P, New B M. Settlement above tunnels in the United Kingdom—their magnitude and prediction[C]// Proceedings of Tunnelling 82. London: Institution of Mining and Metallurgy, 1982: 173−181.
[12] New B M, O'reilly M P. Tunneling induced ground movements: predicting their magnitude and effects[C]// Processdings of the 4th International Conference on Ground Movements and Structures, Cardiff. London: Pentech Press,1991: 671−697.
[13] O'Reilly M P, Mair R J, Alderman G H. Long-term settlements over tunnels: An eleven-year study at Grimsby[C]// Proceedings of Conference Tunnelling. London: Institution of Mining and Metallurgy, 1991: 55−64.
[14] 刘建航, 侯学渊. 盾构法隧道[M]. 北京: 中国铁道出版社, 1991: 329−639. LIU Jianhang, HOU Xueyuan. Shield tunnel[M]. Beijing: China Railway Press, 1991: 329−639.
[15] CAO Z J, WANG Y. Bayesian approach for probabilistic site characterization using cone penetration tests[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2013, 139(2): 267−276.
[16] WANG Y, CAO Z J. Probabilistic characterization of Young’s modulus of soil using equivalent samples[J]. Engineering Geology, 2013, 159: 106−118.
[17] CAO Z J, WANG Y. Bayesian model comparison and characterization of undrained shear strength[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2014, 140(6): 014−018.
[18] 张湾, 李典庆, 曹子君. 基坑开挖参数反分析贝叶斯方法比较研究[J]. 武汉大学学报(工学版), 2016, 49(6): 806−811. ZHANG Wan, LI Dianqin, CAO Zijun. Comparative study of Bayesian methods for back analysis of deep excavation[J]. Engineering Journal of Wuhan University, 2016, 49(6): 806−811.
[19] QI X H, ZHOU W H. An efficient probabilistic back-analysis method for braced excavations using wall deflection data at multiple points[J]. Computers and Geotechnics, 2017, 85: 186−198.
Reliability analysis of shield tunneling empirical model based on Bayesian updating
WU Bo1, DENG Zheng1, HUANG Wei1, LI Zhigang2, ZHANG Ziyi1
(1. Key Laboratory of Disaster Prevention and Structural Safety of the Ministry of Education,College of Civil Engineering and Architecture, Guangxi University, Nanning 530004, China;2. Sinohydor Bureau 1 Co., Ltd, Changchun 130062, China)
A Bayesian updating method considering the uncertainty of the empirical model is used. The model deviation coefficient was regarded as a random variable, and it was updated continuously by using the field observation data. The updating results can be used to predict the maximum surface settlement and failure probability of foundation pit excavation in the subsequent stage. Taking a section of Fuzhou Metro Line 6 as an example, the proposed method was applied to Peck model, O'Reilly-New model, and Peck model modified by Liu Jianhang. The results show that the three models generally overestimate the maximum surface subsidence, among which Peck model has the largest deviation, followed by Liu Jianhang’s revised Peck model, and O'Reilly-New model has the smallest deviation, while the variability of Liu Jianhang’s revised Peck model is smaller than that of O′Reilly-New model, and the influence of model uncertainty can be effectively considered by the proposed method.The results of the modified Peck model are more accurate than those of the other two models. In the case study, the monitoring data increase with the excavation, which reduces the uncertainty of the model deviation coefficient and soil parameters, and ultimately leads to the decrease of the failure probability of shield tunnels.
shield tunnel; maximum surface subsidence; Bayesian updating; failure probability; monitoring data
U231
A
1672 − 7029(2020)04 − 0957 − 08
10.19713/j.cnki.43−1423/u.T20190598
2019−07−03
国家自然科学基金面上资助项目(51478118,51678164);广西自然科学基金资助项目(2018GXNSFDA138009);广西科技计划项目(AD18126011);广西特聘专家专项资金资助项目(20161103)
吴波(1971−),男,四川阆中人,教授,从事隧道与地下工程技术研究;E−mail:gremms@126.com
(编辑 阳丽霞)

