基于非合作博弈的公交出行结构优化分析

徐 婷, 姜瑞森, 温常磊, 张 香, 王 健

(长安大学汽车学院，西安 710064)

轨道交通和常规公交作为交通系统的两个重要组成部分近年来得到了长足的发展，其中轨道交通凭借其运行速度快、荷载能力强等特点构成了许多城市公交线网的“骨架”，然而线网密度却相对较低。因此，如何将常规公交与轨道交通相结合，在以轨道交通为“骨架”的城市公交线网中充分发挥常规公交的通达性、灵活性等特点是一项重要的研究内容。通过合理分配公共交通资源，合理配置常规公交和地铁，对优化公共交通出行结构、提高居民公交服务水平、节能减排具有深远的意义。目前有关于公共交通出行结构优化方面的研究主要从数学模型和影响因素两方面进行。博弈论模型、结构约束模型等先进的数学思想近年来广泛的应用于公共交通出行结构优化方面的有关研究[1-2]。考虑到最优城市公共交通出行结构的影响因素，基于城市空间结构、居民出行成本等因素对公交出行结构分析也是近年来国内外研究的重点[3-5]。胡继华等[6]利用公交刷卡数据分析居民的公交出行结构；孙文霞等[7]为了提倡公交优先策略对公交专用道的铺设进行了研究。然而将两者结合起来的有关研究却相对较少，运用博弈论的有关思想[8]，以居民的出行成本最小为优化目标构建博弈模型预测最佳公交分担率，在公共资源有限的大前提下寻求公共交通出行结构的纳什均衡点，具有深刻的研究意义。

针对轨道交通和常规公交两种常见的公共交通形式构建基于非合作博弈的公共交通出行结构优化模型，以居民出行成本最小作为优化目标对模型求解，结合项目对研究区域的实际调研数据进行分析，得出以出行收益最大为目标的公共交通出行结构，以此为根据对城市的公共交通出行结构优化提供参考和建议。

1 构建博弈模型

1.1 问题描述

目前城市公交规划的有关研究中，常常使用“长距离出行使用地铁作为出行工具，中、短距离出行选择通达性更好的常规公交作为出行工具”这一概念对公交结构进行优化，然而面对有些情况该种公共交通出行结构并不适用。

随着城市规划中“功能分区”的概念逐渐增强，某些短距离区域的公共交通出行需求急剧增长，单纯利用常规公交完成运输任务会造成公交服务水平下降、线路运力不足、道路拥挤、乘客等车时间增长等问题，因此需要在该段区域建设有关轨道交通设施，分担常规公交运输压力。典型代表是北京市地铁9号线，其全长16.5 km，远低于北京市地铁线路平均长度27.99 km。相反，为了使城市结构更加紧凑，随着城市规划许多城市的住宅区距离城市中心商业区相对较远，虽然两功能分区公共交通出行需求极大，但由于沿途出行需求较低，建设轨道交通成本较高，所以应采用定制公交等成本较小的常规公交形式完成运输任务。

针对上述问题，拟对出行者按照长距离出行，中、短距离出行进行分类[9]，运用博弈论的有关思想，在公共交通资源有限的前提下以出行者收益最大为目标构建非合作博弈模型，为优化城市公交线网提供建议。

1.2 收益函数建立

出行者的出行成本主要由出行费用、出行时间以及舒适度等3个因素组成，为了统一出行者出行成本，对出行费用、出行时间以及舒适度3项因素进行归一化处理，具体成本为

xi=αiTi+βiCi+Ei

(1)

式(1)中：xi为出行者选用i接驳交通方式的出行成本；Ti为出行者选用第i种接驳交通方式的乘车时间，min；Ci为出行者选用第i种出行方式的舒适度；Ei为出行者选用第i种出行方式的出行费用，元；αi是第i种接驳交通方式的时间价值系数;βi为第i种接驳交通方式的舒适度价值系数。

出行者的出行时间主要由换乘时间(Nt)和乘车时间(Vt)两部分组成，由于共享单车的出现，所以居民换乘所采用的接驳方式大致可分为步行和骑自行车两种，出行时间Ti的计算公式为

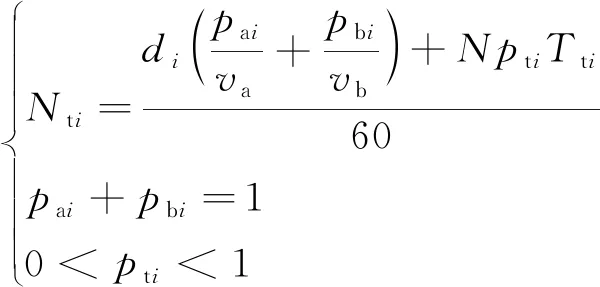
(2)

(3)

Ti=Nti+Vti

(4)

式中：di为该种交通方式线路站点平均站距，m；va和vb为城市居民步行和骑自行车平均速度，m/s；pai和pbi为步行和骑自行车出行者占总出行乘客人数的比例;N为平均换乘次数；pti是换乘出行者占总出行者的比例；Tti是换乘平均损失时间，s;D为出行者的出行距离，km;di为该种接驳交通方式线路站点平均站距，m；vi是该种接驳交通方式的平均车速，km/h；Tsi为经停站点平均损失时间，s。

乘客出行的舒适程度取决于车辆的拥挤程度，所以使用平均每位站立乘客所占的有效面积表示车辆的拥挤程度，查阅相关文献资料[10]，拥挤度主要分为3个等级，根据不同决策下的拥挤程度，本模型分别采用出行成本的10%和20%作为舒适度成本，即当不拥挤时舒适度不受影响，一般拥挤的舒适度成本为该种交通方式广义出行方式出行费用的10%；严重拥挤的舒适度成本为该种交通方式广义出行方式出行费用的20%，具体如表1所示。

表1 拥挤度判定标准Table 1 Criterion of congestion degree

1.3 构建博弈模型

针对公共交通出行结构优化进行分析，所以仅考虑选择公共交通方式出行的出行者作为研究对象。模型假设研究区域共有n个出行者使用公共交通出行，将n个出行者出行按照距离分为中、短距离出行和长距离出行；在博弈中，n个出行者可以选择轨道交通出行或乘坐常规公交出行，假设乘坐轨道交通出行的人数占总人数比例为x，则选择常规公交出行的人数占总人数比例为(1-x)，分别对不同人群进行收益分析。

结合混合策略纳什均衡有关定义和2.2节中出行者出行成本分析，给出“局中人”长距离出行者和中、短距离出行者选择分别选择不同出行方式的出行成本，Ai、Bi分别表示中、短距离出行者和长距离出行者的出行成本，i=1,2,3,4依次表示双方都选择常规公交出行；中、短距离居民选择常规公交出行，长距离居民选择地铁出行；中、短距离居民选择地铁出行，长距离居民选择常规公交出行以及双方都选择轨道交通出行等4种情况。具体出行成本矩阵如表2所示。

表2 不同出行距离出行者成本矩阵Table 2 Traveler cost matrix with different distances

根据非合作动态博弈有关定义，假设中、短距离出行者出行的混合策略为σ1=(θ，1-θ)，即中、短距离出行者选择常规公交出行的可能性为θ，选择地铁出行的可能性为(1-θ)；长距离出行者出行的混合策略为σ2=(γ，1-γ)。

给定γ，中、短距离出行者选择常规公交出行(θ=1)和使用地铁出行(θ=0)，长距离出行者的期望收益分别为

π(1,γ)=B1γ+B3(1-γ)

(5)

π(0,γ)=B2γ+B4(1-γ)

(6)

给定θ，长距离出行者选择常规公交出行(γ=1)和使用地铁出行(γ=0)，中、短距离出行者的期望收益分别为

π(θ,1)=A1θ+A2(1-θ)

(7)

π(θ,0)=A3θ+A4(1-θ)

(8)

当π(1，γ)=π(0，γ)；π(θ，1)=π(θ，0)时，解得γ*、θ*为

(9)

(10)

经分析讨论，如果中、短距离出行乘客选择常规公交出行的概率小于γ*，那么长距离出行者出行的出行方式最优选择常规公交出行；如果中、短距离出行乘客选择常规公交出行的概率大于γ*，那么长距离出行者出行的出行方式最优选择是地铁出行；如果中、短距离乘客选择常规公交出行的概率是γ*，长距离出行乘客自由选择出行方式。同理可解出长距离出行乘客出行方式选择概率。

2 太原市出行结构优化

太原市地铁正在快速发展，加入地铁出行方式后的公共交通出行结构尚未确定，急需优化。因此选择太原市进行案例分析，根据相关资料查阅及问卷调查分析的方式，结合非合作博弈模型对太原市的最佳公交分担率进行预测。

参考《城市公共交通分类标准》(CJJ/T 114—2007)以及《城市道路交通规划设计规范》(GB/T 51328—2018)相关标准，结合在太原市发放调查问卷以及相关文献资料的查找，本模型所需参数如表3所示。

2.1 出行时间成本分析

参考文献[11]结合实际情况，模型中选用常规公交的出行时间价值系数为15元/h，地铁出行时间价值系数为21.6元/h，结合模型计算的长距离居民、中短距离居民出行情况，不同“局中人”的出行时间成本如表4所示。

2.2 出行费用成本分析

太原市目前大部分公交采用一票制，所以假设乘坐常规公交的票价仅与换乘次数有关，单程常规公交票价为1元，综合表3中常规公交的换乘人数、换乘次数相关比例，其常规公交的出行费用为1.63元。出行者选择哪种出行方式主要取决于出行者的出行距离，由于太原市地铁正在建设中，其票价参考中国类似城市地铁定价标准。设定中、短距离出行者平均出行费用为3元；长距离出行的出行者平均出行费用为5元。不同出行方式的费用如表5所示。

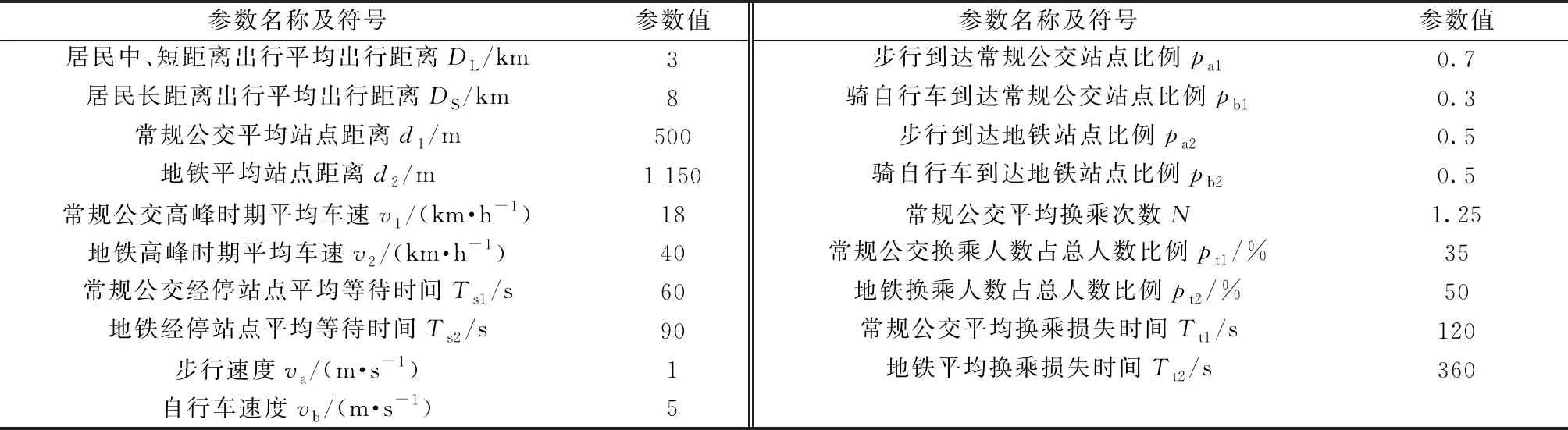
表3 收益模型参数值Table 3 Revenue model parameters

表4 不同出行距离出行者出行时间成本Table 4 Travel time cost with different distances

表5 不同出行距离出行者出行费用Table 5 Travel costs with differentdistances

2.3 舒适度成本分析

模型选取太原市基础数据进行分析，太原市如果乘客全部选择常规公交、地铁出行，高峰时期每位站立乘客的有效面积分别为0.175 m2/人和0.08 m2/人，分别属于一般拥挤和严重拥挤，结合常规公交、地铁的广义出行费用，不同出行距离出行者舒适度成本如表6所示。

根据对太原市有关研究区域的调查研究，经计算得出不同类型收益的具体收益值，代入式(9)、式(10)，计算出γ*=61.34%，θ*=53.18%，由于计算出的γ*、θ*都在(0,1)，即模型拥有实际意义，经讨论研究：61.34%的中、短距离出行居民选择常规公交出行；53.18%的长距离出行居民选择常规公交出行。该种公交出行结构出行者的收益最高，具体如表7所示。

表6 不同出行距离出行者舒适度成本Table 6 Comfort cost with different distances

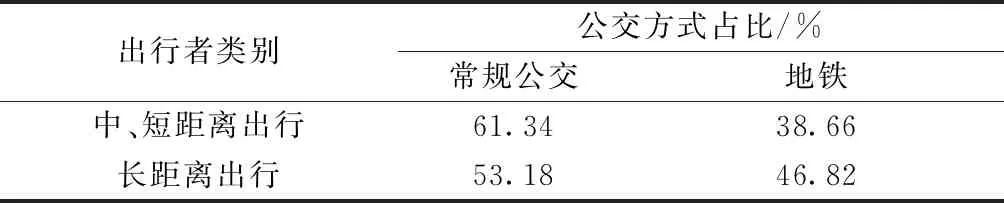
表7 太原市公共交通出行结构优化Table 7 Optimization of public transport structure in Taiyuan

3 结论

通过对按距离分配的出行者出行方式选择划分的混合策略的纳什均衡模型进行分析讨论，可以得出以下结论。

(1)按照模型中假设的出行收益模型，其混合策略纳什均衡计算结果符合实际，即具有纳什均衡点，该模型应结合研究区域的实际情况对有关参数进行计算，得出符合实际情况的该模型的纳什均衡。根据模型的纳什均衡点分析讨论得出，并不是每种出行距离下选择固定出行方式即为最佳方案，过多人选择同种交通方式会导致拥挤、公共交通服务质量差等问题，会使出行者的出行收益减少。合理的公共交通出行结构可以为公交线网的规划提供参考和帮助。

(2)以太原市作为案例进行分析，通过相关资料研究以及实际调研的方式采集模型相关数据，经检验模型具有实际意义，最终最佳公交出行结构为61.34%的中、短距离出行居民选择常规公交出行，53.18%的长距离出行居民选择常规公交出行。以此为依据对太原市公交线网优化提供建议，针对正在建设的地铁以及常规公交进行调整，通过增加区间线路或大站快车的方式对居民出行进行诱导，尽量使城市不同出行距离出行者出行方式选择符合最优比例。

(3)模型不仅仅适用于正在建设或计划建设地铁的城市，以拥有地铁城市的有关部门也可以根据该预测模型得出中、短距离出行者和长距离出行者不同出行方式人数比例从而对城市出行居民进行出行方式选择的有关引导。例如，在公交需求量大的有关区域建设地铁区间线路，交通需求相对稳定的交通片区之间可以建立固定班车线路以提高出行者出行效率，建立与地铁线路拥挤路段线路相同的公交线路以缓解地铁运输压力等方法调整出行方式选择比例，力求出行者的出行收益最大化。

根据上述结论，针对城市公共交通规划提出了一种新的思路，利用出行距离对出行者进行分类，使用混合策略纳什均衡找到不同类型出行者出行收益最大化的纳什均衡点并以此为基础对公共交通线网进行优化以提高公共交通竞争力。当然，从出行者按照距离分类的角度建模，有些条件设置较为理想，如仅用两种距离划分出行者的出行行为等。结合研究区域特点构建更准确的优化模型是今后的研究重点。