基于史密斯预估补偿及自整定PID 的过热汽温控制方案
焦 健
(北京源深节能技术有限责任公司,北京 100036)
0 引言
过热汽温是火电机组运行中的一项重要参数,其控制品质的优劣会对机组的安全性和经济性产生较大影响。从控制角度来说,过热汽温这一被控对象通常表现出大迟延、非线性等特性,给控制带来不小难度。目前,火电厂多采用比例-积分-微分PID(proportion integration differentiation)串级控制策略,将过热汽温划分成导前区和惰性区两个环节,分别采用主副PID 控制器进行控制[1]。这种控制方案简便易行,但存在以下不足之处[2]:一是PID 参数整定较为复杂烦琐,现场整定时首先整定副调节器参数,待内回路稳定后再整定主调节器参数,使外回路稳定,整定方法多采用临界比列带法,并根据调试人员的工程经验进行试凑[3]。这一步骤十分烦琐,耗时长,效果受限于工程经验,且整定结果不是最优,仍存在很大的优化空间。二是被控对象的大迟延特性没有得到很好解决,即使采用串级控制,在变工况运行中,过热汽温控制仍存在汽温变化缓慢、偏差大等问题,不能满足电厂小指标考核等要求。
为解决这两个问题,本文提出了一种基于自整定PID 及史密斯预估补偿的过热汽温控制方案。该方案相比传统的控制策略进行了两方面的改进,首先是采用史密斯预估器对过热汽温的惰性区大迟延特性进行补偿,对串级控制方案做出调整,将2 个PID 控制器缩减为1 个。其次是采用梯度下降法的径向基函数RBF(radial basis function)网络,确立优化函数,对PID 控制器进行自整定,取代调试人员的手动整定过程。仿真结果表明,改进的过热汽温控制方案能有效克服传统方案的不足之处,系统输出动态响应快,超调量小,并能够对PID 参数进行自整定,在减小工作量的同时优化了参数,提高了最终的控制效果。
1 史密斯预估器补偿原理
很多工业过程的控制对象含有大滞后的特性,这种滞后使得控制系统稳定性降低,动态响应差,易引起超调和震荡,从而给控制器设计带来困难。为此,需要对滞后环节做出补偿[4]。
史密斯预估器是一种应用较为广泛的对纯滞后对象进行补偿的控制方法,在实际应用中,具体做法是给PID 控制器并联一个补偿环节,该补偿环节称为史密斯预估器。其具体作用是在系统的反馈回路中引入补偿装置,将控制通道传递函数中的纯滞后部分与其他部分分离。
设被控对象的传递函数为

其中,GP(s)为传递函数中不含纯滞后的部分;e-τs为传递函数中的纯滞后部分。
系统控制结构如图1 所示。
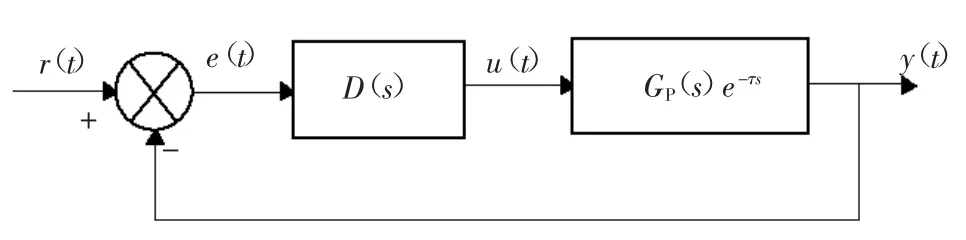
图1 系统控制框图
史密斯预估器就是增加1 个与控制器D(s)并联的环节进行补偿,补偿后的回路如图2 所示。

图2 补偿后的系统控制框图
补偿环节的传递函数为
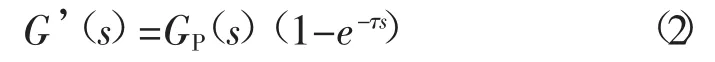
由补偿环节与控制器D(s)组成的传递函数为

系统等效传递函数为

从控制系统的等效传递函数中我们可以看出,系统的滞后特性移动到了闭环传递函数之外,系统的特征方程不再包含大滞后环节,相当于无滞后系统,其控制的稳定性得到提高[5]。
2 基于RBF 网络的自整定PID 算法
2.1 RBF 神经网络结构及训练方法
RBF 网络是一种前馈神经网络,通常为3 层结构,如图3 所示。网络具有n个输入,h个隐节点和m个输出。
图3 中,x为网络输入,c为隐节点的中心,Φ 为隐节点的基函数,W为输出权矩阵,b为输出单元偏移,y为网络输出。在本文中,采用高斯函数作为隐节点的基函数,如式(5) 所示。

图3 RBF 网结构

其中,δ 为基函数的扩展常数。图3 中,i表示第i个隐节点,RBF 网络的第k个输出可表示为


在式(7) 中,β 表示遗忘因子;对第j个学习样本,e为误差信号,其计算式为

考虑到所有的学习样本,隐节点中心、扩展常数和权值的调节量为

在上述公式中,Φi(Xj)表示第i个隐节点对第j个输入样本的输出,η 为学习率。
2.2 RBF 网络整定PID 参数
采用RBF 网络进行PID 参数整定时,输出设定值为r,第k时刻输出偏差为

可以采用输出偏差的平方作为性能指标函数,使目标函数最小。

对增量型PID 控制器,控制量增量Δu离散化表达式为

其中,Kp、Ki和Kd表示比例、积分和微分系数,RBF 网络的输入包含3 个值,表达式为

则每次训练完神经网络后,可以根据新的网络参数来对PID 参数进行调整,本文中同样适用梯度下降法来计算[7]
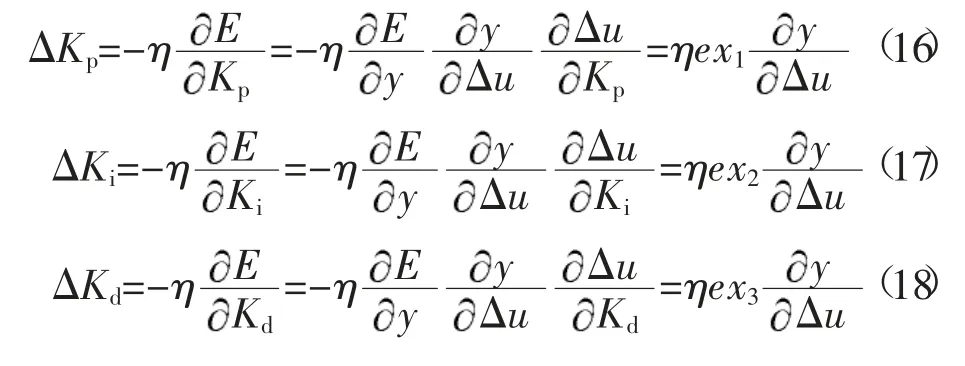
其中,系统输出对控制量增量的偏导数可以用网络输出对网络输入的偏导数近似,其表达式为
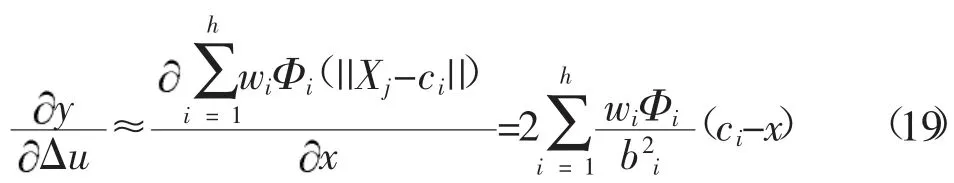
3 仿真实验
3.1 RBF 网络训练
为验证本文算法,我们以过热汽温作为被控对象进行仿真实验。设导前区和惰性区的传递函数分别为

结合史密斯预估器,改进控制方案如图4 所示。

图4 改进过热汽温控制方案
设仿真时间为2 000 s,每次训练样本数N=2 000 个,隐节点数h=10 个,对设定值进行阶跃扰动,训练RBF 网络,网络训练曲线如图5 所示。
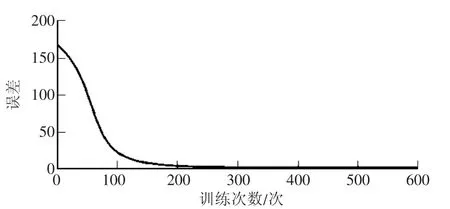
图5 网络学习曲线
由图5 可以看出,误差曲线随着训练次数增加不断下降,目标函数最终收敛,达到了所允许的最小偏差,网络训练完成。
3.2 改进控制方案与原方案仿真对比
在得到了经训练后的PID 控制器参数后,我们对控制系统分别进行了设定值、导前区和惰性区的阶跃扰动实验,并与原串级控制方案进行比对。
a) 首先对设定值进行阶跃扰动,输出响应曲线如图6 所示。

图6 设定值扰动下输出响应曲线
由图6 可以看出,在设定值发生扰动时,改进的方案相比于原方案调节平稳,没有超调,且响应时间也略快于原方案。
b) 在仿真时间200 s 时对导前区输出施加一个阶跃扰动,仿真结果如图7 所示。
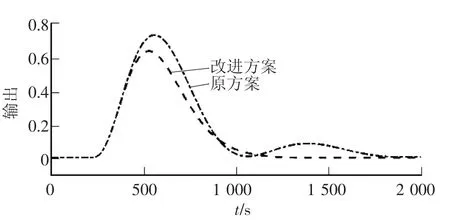
图7 导前区扰动输出响应曲线
由图7 可以看出,在导前区输出发生扰动的情况下,改进方案的抗干扰能力要优于原方案。
c) 对惰性区的输出施加阶跃扰动,仿真结果如图8 所示。

图8 惰性区扰动下输出响应曲线
由图8 可以看出,当惰性区输出发生扰动时,改进方案的输出曲线能较快回到设定值且没有振荡,抗干扰能力更强。
4 结束语
本文以燃煤机组过热汽温控制为背景,研究了史密斯预估和RBF 网络自整定PID 方法在这一领域的应用。首先,介绍了史密斯预估器的基本原理,并利用预估器对过热汽温惰性区的滞后特性进行补偿,将传统的串级控制方案改成带补偿环节的单PID 控制方案。然后介绍了基于梯度下降法的RBF 网络训练方法,并应用于PID 控制器的参数自整定上。最后,将上述的两种方法结合起来,训练RBF 网络得到PID 参数,并进行仿真实验。仿真结果表明,与原方案对比,改进的过热汽温控制方案在设定值发生变化时,输出响应更快,且控制平稳,没有超调。在抗扰动能力方面,无论是导前区还是惰性区发生输出扰动,改进控制方案的效果要优于原来的串级控制方案。此外,本文提出的PID 自整定方法相比于传统的PID 参数调节方法更为简单,可通过计算程序直接获取最优的PID 参数,调参速度更快,可以缩短调试周期,减少调试人员的工作量。

