面向冗余量测的台区低压配电网潮流计算及应用
张 旭,夏 燕,章江铭,章坚民,汪东耀,郑宇峰
(1.国网浙江省电力有限公司电力科学研究院,杭州 310014;2.杭州电子科技大学 自动化学院,杭州 310018;3.国网浙江海宁市供电有限公司,浙江 海宁 314000;4.浙江华云信息科技有限公司,杭州 310012)
0 引言
以公变为主供电源的低压台区配电网是供电部门向广大低压用户提供高质量电能的最低一级配电网。潮流计算是其运行态势的感知,包括电压质量、理论线损及统计线损、量测差错、拓扑差错、偷窃电分析等应用的重要基础计算[1]。低压台区配电网呈现简单的辐射状拓扑,线路电阻与电抗的比值较大。公变低压侧采取基于公变终端的电气电能量量测,相对精度较低,而末梢用户采取计量用的智能电表,相对精度较高,但是存在冗余量测。
低压配电网具有许多不同于高压输电网的特征[2],例如:环网结构,开环运行,正常运行时呈辐射状;支路参数的比值较大;三相支路参数不对称和三相负荷不平衡问题比较突出;网络的PQ 节点多,PV 节点少等。由于配电网一般呈辐射状,潮流计算通常采用前推回代法[3-4]、牛顿—拉夫逊法[5-6]和改进的前推回代法[7-9]。由于牛顿—拉夫逊法在计算配电网的潮流时呈现一定程度的病态,因此收敛效果不理想。在配电网中运用快速解耦法时,也由于无法满足PQ 分解条件而难以收敛[10]。前推回代法具有物理概念明晰、简单且易实现、收敛性较好等特点,适合于求解辐射状配电网潮流。
随着用电终端智能电表的大规模接入和应用,供电部门的数据呈指数级增长,其中的负荷数据在设计规划、生产调度、供电能力评估、负荷预测、电能质量、潮流计算等方面都有着广泛的应用。配电网负荷数据具有以下特点[11]:一是高并发性,远方监测终端对象数量庞大且分布广泛,基于非循环式远动规约同时提交负荷数据,流量惊人;二是时序性强,数据在采集、传输、分析和存储过程中以数据流的形式持续出现,需要以尽可能高效的方式对数据进行即时处理;三是数据处理代价高昂,负荷数据一般为高精度浮点数且数值敏感性较强,同时配电网分析算法复杂,需要大量硬件资源才能实现负荷数据的传输与处理[11]。但数据在采集时存在内在的出错倾向,在大量数据集中时,数据错误、数据缺失现象极其普遍。除了传统的加权残差法、量测量突变检测法、目标函数极值检测法等,近几年也有不少学者提出其他方法进行坏数据识别和修复。文献[12]采用改进的模糊C 均值聚类的方法对历史数据进行聚类后识别异常数据并修正;文献[13]利用内点法求解最优潮流得到状态估计值的方法对DMS(数据库管理系统)数据进行坏数据的识别和修复;文献[14]提出了基于时间序列分析的双循环迭代校验法进行输变电设备状态大数据清洗;配电网数据往往是多源的、多渠道的,如来自SCADA(数据采集与监控)系统的数据和PMU(同步相量测量装置)的数据。文献[15]针对多源时空数据,提出多源时空信息数据匹配、对比的方法进行坏数据识别清洗。同时,以上文献中所提方法都需要大量的历史数据。
为此,本文首先结合低压配电网特点和冗余量测,提出了基于功率量测和基于电流量测的潮流计算方法,并对其误差进行了分析。同时通过两类计算结果与实际量测的对比,可以对实际的冗余量测进行校验,剔除量测坏点。
1 台区低压配电网特点分析
1.1 接线分析和拓扑定义
对于中压配电网,其静态拓扑变动频度很低,但是由于存在大量的开闭所、环网柜、联络开关和联络线,因此潮流计算前必须根据静态拓扑和开关位置,搭建相应适合潮流计算的动态拓扑,一般采取主干-支干拓扑模型。
与中压配电网相比,低压配电网拓扑结构相对更简单,节点也不多,树支特征更为明显。由于无联络线,因此其动态拓扑与静态拓扑是一致的。但是,由于新增用户、用户增容、三相平衡等需求,存在一定频度的改接线,为此,设计一种简单的节点-线段关系非常有必要。因此,本文提出最简单的拓扑定义,如表1 所示,便于相应的管理信息系统录入。

表1 低压配电网拓扑关系
1.2 智能电表量测及冗余分析
智能电表量测记录数据呈多样化,主要分为以下六大类[16]:电量类数据,如总电能示值、各费率电能示值、最大需量等;负荷类数据,如电压、电流、有功功率、无功功率、功率因数等;事件类数据,如终端和电表的各种事件和报警;工况数据,如采集终端及计量设备的工况信息;电能质量类数据,如功率、电压、谐波等;另外还有费控信息等其他数据。
低压配电网用户智能电表记录功率、功率因数、电压、电流信息4 个参数,只要知道其中2个即可推导其余参数,潮流计算也仅仅需要其中2 个参数,即智能电表的量测数据对潮流计算来说存在冗余项,因此可以利用不同的潮流计算来校验其他参数的正确性。
1.3 潮流计算方法选择
对于台区低压配电网而言,由于原始点线关系存在一定频度的变动,因此采取基于路径搜索的潮流计算,以适应网络拓扑结构的动态变化。
同一台区所有智能电表在获取数据的过程中,不能完全做到同步采集,采集到的数据会有错误,因此可以利用冗余数据互相校验正确性,将错误的数据修正后再进行潮流计算。
将配电变压器低压侧的电压、电流、有功、无功数据作为首端(电源端)数据项,使用用户智能电表的电压、电流、有功、无功数据作为末梢段的数据项,本文提出基于电流和基于功率的两种潮流计算方法,并对结果进行相互校验以修正错误数据。
2 潮流计算基本原理
2.1 前推回代法
前推回代法是一种常用的求解配电网潮流的支路类算法。在低压配电网的量测数据中,源节点电压、功率和节点负荷是已知的。根据配电网辐射状的特点,前推回代法潮流计算由前推和回代2 个过程组成,其中前推过程用于求解各支路电流或各节点功率,回代过程用于求解各节点电压。本文中前推回代法的前推过程采用基于节点注入电流(方法1)和节点注入功率(方法2)两种方法,回代过程均为求解节点电压。首先假设整个电网所有节点的电压均为额定电压,然后根据基尔霍夫定律依次计算每条支路的电流和功率损耗,从而得到首端的初始功率和各条支路的电流,以上就是回代的整个流程。接着根据给定的首端电压和回代所得的初始功率,计算从首端到末端每条支路的电压降,得到每个节点的电压,以上是前推的整个流程。
重复前推和回代两个过程,直至满足收敛条件为止。
2.2 路径搜索算法
DFS(深度优先搜索)算法是搜索算法的一种[17]。它沿着树的深度遍历树的节点,尽可能深地搜索树的分支。当节点i 的所有边都已被探寻后,搜索将回溯到发现节点i 那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点,则选择其中一个作为源节点并重复以上过程,整个过程反复进行直到所有节点都被访问为止。DFS属于盲目搜索。
图1 为本文提出的路径搜索算法流程,由DFS 算法修改而来,其目的是计算前推回代法潮流计算中的回代求节点电压,算法过程如下:
Step1:搜索根节点和与根节点相连接的子节点,若子节点号大于1 个,则记录下子节点号及对应的第i(i≥2)条根节点号及子节点号,并计算第一个子节点号的节点电压。
Step2:搜索与Step1 中子节点号相等的父节点号,若父节点号大于1 个,则记录下这个父节点号及对应的第i(i≥2)个子节点号,并计算这个父节点号对应的第一个子节点号的节点电压。重复这个过程直至该条路径的末梢节点。
Step3:从Step2 中记录的最后一条未被访问的父节点和子节点开始计算该子节点的节点电压,并删除该条记录。
Step4:重复Step2 和Step3,直至所有未被访问的父节点号和首节点号都没有为止。
2.3 算法流程
2.3.1 基于节点注入电流的前推回代法
基于节点注入电流的前推回代法潮流计算的算法流程如图2 所示。
具体计算过程如下:
(1)首先设置网络中所有节点的初始电压均为额定电压,然后找到网络中的末梢节点(节点类型为1),并将其作为起始点,则可根据欧姆定律求出其注入电流为:

(2)找到各支路的首尾节点,则该支路的支路电流即尾节点连接的各个支路的电流之和为:
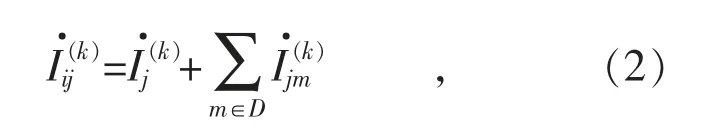

图1 路径搜索算法计算节点电压流程

图2 基于节点注入电流的前推回代法计算流程
式中:节点i 是节点j 的父节点;k 是迭代次数。
(3)已知根节点的电压,则根据路径搜索算法和欧姆定律逐个求得各个子节点的节点电压为:

式中:i 为j 的父节点;Zij为节点i 与节点j 之间支路的阻抗。由式(3)可以逐个求得各个节点的电压,直到末端电压为止。至此,完成了一次完整的前推回代的迭代过程。
(4)计算每次迭代过后电压差值为:

(5)收敛条件为:

当达到式(5)的收敛要求时,结束计算并输出结果,否则,重复步骤(1)—(5)直到满足收敛条件为止。
2.3.2 基于节点注入功率的前推回代法
基于节点注入功率的前推回代法潮流计算的算法流程如图3 所示。具体计算过程如下:
(1)首先设置网络中所有节点的节点电压均为额定电压,然后找到网络中的末梢节点(节点类型为1),并将其作为子节点,根据欧姆定律可求出其父节点的注入功率及该支路的功率损耗为:
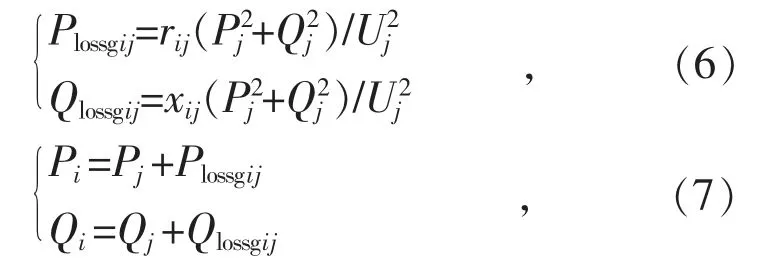
式中:节点i 是节点j 的父节点。
然后将上述父节点作为子节点,求出其父节点的注入功率及该支路的功率损耗,重复以上过程直至源节点。
(2)根据源节点的功率和电压,再根据路径搜索算法和欧姆定律逐个向末梢节点求得各个子节点的节点电压为:

式中:i 是j 的父节点。由式(8)可以逐个求得各个节点的电压,直到末端电压为止。至此,完成了一次完整的前推回代的迭代过程。
(3)计算每次迭代过后电压差值为:

(4)收敛条件为:

(5)节点功率角为:

图3 基于节点注入功率的前推回代法计算流程
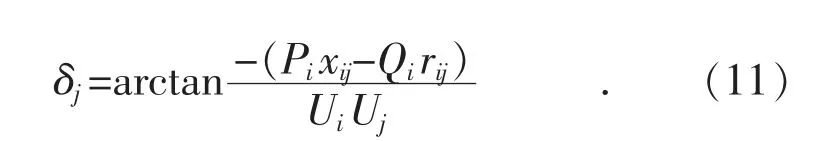
当达到式(11)的收敛要求时,结束计算并输出结果,否则重复步骤(1)—(5)直到满足收敛条件为止。
3 案例分析
3.1 案例说明
本文以某县某台区低压配电网为例,其主电路拓扑如图4 所示,图中主干线部分采取线径为LGJ-70 或LGJ-50 的导线,线路长度在图中已标出,因此可以计算出线段的电阻、阻抗;主干线节点数为51,单相、三相用户数分别为57,9户;受篇幅限制,在正文中不一一列出详细的拓扑关系表及电气参数、负荷参数。
3.2 潮流计算结果
以T 台区8 月27 日00:00 时刻A 相电压为例,用户智能电表量测电压与潮流计算电压的对比情况见表2。表中based I*,based P*分别表示基于电流和基于功率的潮流计算电压和实际电压偏差。
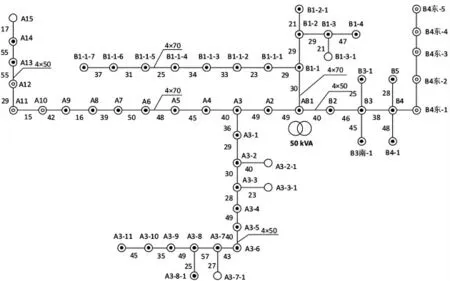
图4 案例台区低压配电网主电路拓扑
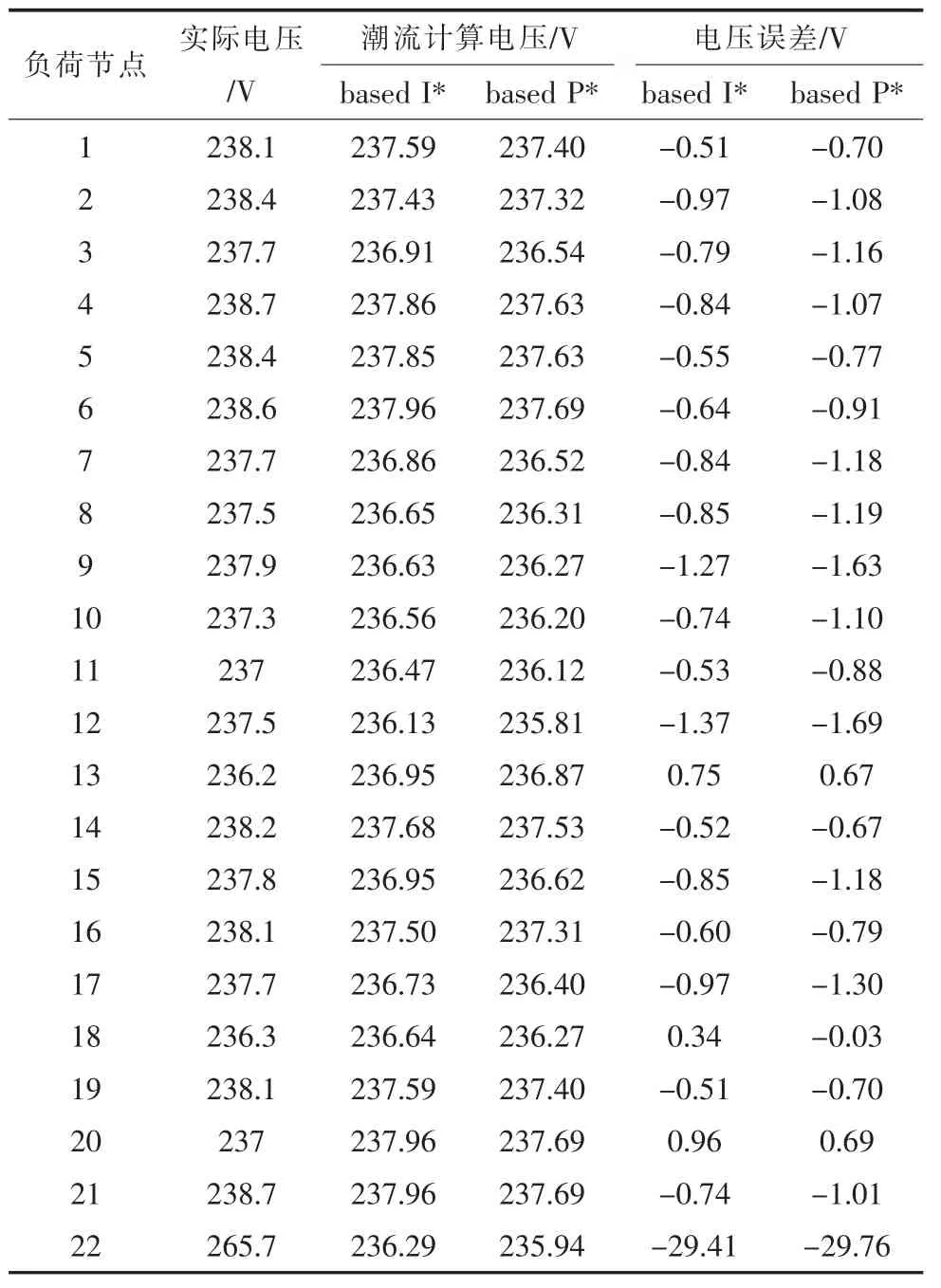
表2 00:00 时刻潮流计算的电压与实际电压的对比
从表2 可以看出,负荷22 的实际电压为265.7 V,方法1 和方法2 两种潮流计算得出的电压分别为236.29 V 和235.94 V,电压偏差率分别为11.01%和11.20%,且该负荷注入系统的电流为0,对潮流计算结果没有影响,因此判断该负荷的智能电表量测值为坏值。从图5(a)中也可判断节点22 的智能电表电压量测值为坏值。剔除该坏值后的电压对比如图5(b)所示,平均电压偏差分别为-0.57 V 和-0.84 V,电压偏差率分别为0.24%和0.32%。这表明智能电表的电压量测和潮流计算的电压计算值一致性非常高。
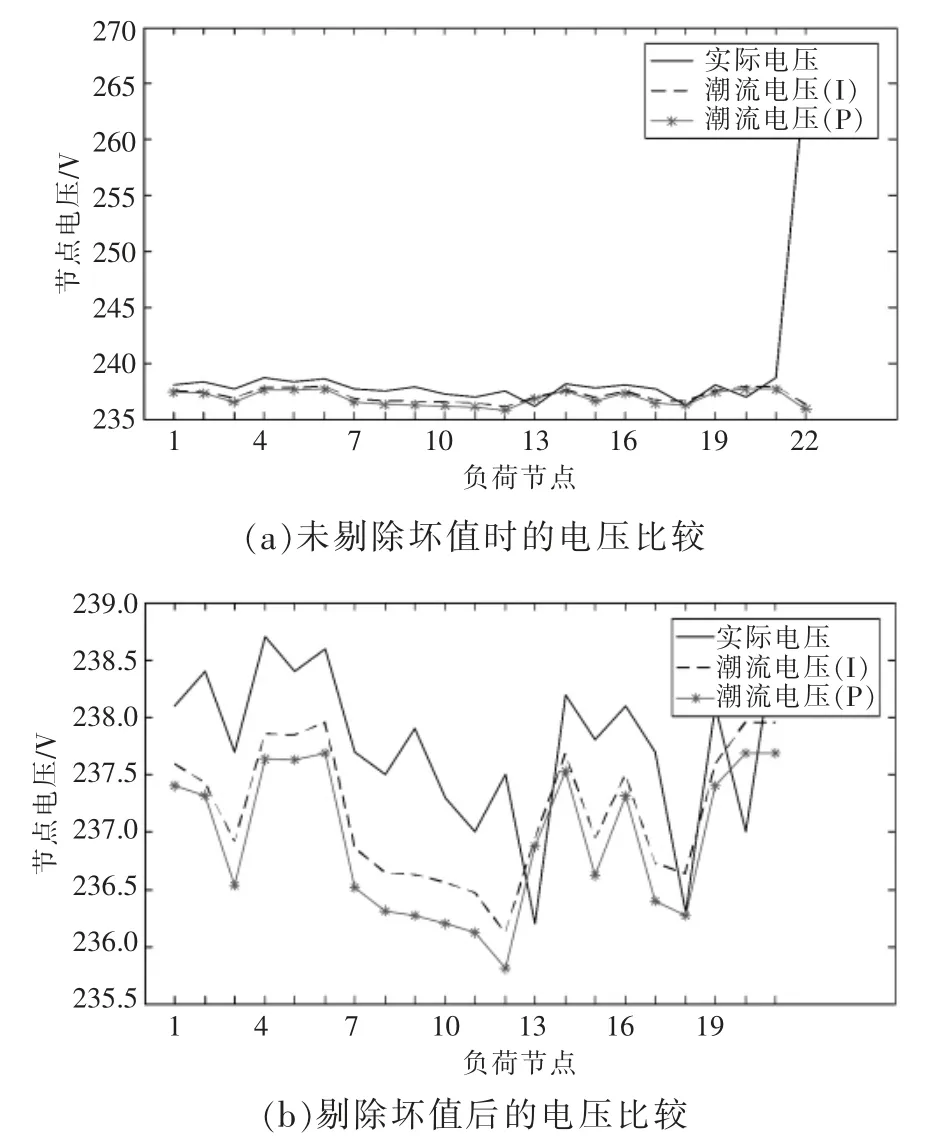
图5 电压比较
00:00 时刻的变压器低压侧A 相智能电表电压量测为238 V,而该时刻系统中不含光伏出力且负荷节点中剔除坏点电压值后最高电压为238.7 V,加上智能电表采集数据时不可避免地存在一定的时间差,因此造成了潮流电压比实际电压普遍偏小。
低压配电网的智能电表每15 min 采集一次数据,一天24 h 共有96 个时刻的数据,即有96组潮流计算结果。T 台区剔除坏点后,采用基于节点注入电流和基于节点注入功率的潮流计算结果对比如表3 所示。

表3 1 天96 时刻2 种潮流计算的结果对比
3.3 潮流计算结果分析
结合表2 和图4,T 台区的原始数据中存在坏点,但由于该坏点注入系统的电流为零,对潮流计算没有影响。假如T 台区的坏点注入系统的电流不为零,则需事先对坏值进行修正后方可潮流计算,以提高潮流计算的精确度。
表2 表明:在同收敛精度同参数的情况下,方法1 的计算结果优于方法2,结果更接近实际的负荷节点电压。但计算时间上方法2 优于方法1。这两种方法的平均电压误差率均小于1%,均能应用于低压配电网的潮流计算。但在节点少的情况下优先推荐使用方法1 进行低压配电网的潮流计算。
低压配电网电压等级低,且具有支路短、支路电阻与电抗比值较大的特点,因此同一支路上的两个节点之间的电压差一般小于1 V,这就要求智能电表的量测精度应至少精确到小数点后1位。在潮流计算的过程中,根节点的电压基值取的是该时刻的公变低压侧智能电表的电压值,但公变低压侧的智能电表电压值只精确到个位整数,精度不满足要求,因此理论上的潮流计算结果具有0.5 V 的误差。
4 结语
本文介绍的两种潮流计算方法均可应用于低压配电网,且基于节点注入电流的潮流计算方法结果优于基于节点注入功率的潮流计算方法,但前者的计算时间比后者长。
当前低压配电网的公变低压侧数据精度较低,造成潮流计算结果存在0.5 V 的误差,若能提高公变低压侧智能电表的量测精度,则可消除这一误差,进一步提高潮流计算的可信度。
由于同一台区的智能电表采集时间不完全同步,采集到的数据难免存在偏差,本文所提潮流计算方法可用于修正偏差较大的数据,也可用于态势渲染图的基础数据。

