温度与微结构高度误差对衍射光学元件衍射效率的影响研究
杨亮亮,赵勇兵,唐 健,郭仁甲
温度与微结构高度误差对衍射光学元件衍射效率的影响研究
杨亮亮,赵勇兵,唐 健,郭仁甲
(盐城师范学院 物理与电子工程学院,江苏 盐城 224007)
基于衍射光学元件的衍射效率与微结构高度误差的关系,提出了环境温度、微结构高度误差与衍射效率和带宽积分平均衍射效率的数学分析模型。研究了环境温度变化对带宽积分平均衍射效率的影响,分析了工作在一定温度范围内时带宽积分平均衍射效率与相对微结构高度误差的关系。对于工作在8~12mm长波红外波段的衍射光学元件,偏离设计波长越远,其衍射效率受温度的影响越大。温度的变化会引起100%衍射效率对应的峰值相对微结构高度误差发生改变。当衍射光学元件的相对微结构高度误差在±15%范围内时,衍射效率在-40℃~80℃的整个温度范围内高于91.89%,带宽积分平均衍射效率在整个温度范围内高于88.58%。
衍射光学;衍射效率;微结构高度误差
0 引言
鉴于衍射光学元件具有区别于传统折射透镜的负色散性质和负热差性质等,所以,其广泛应用于各种成像光学系统中[1-3]。衍射光学元件可以直接采用单点金刚石车削方法进行加工[4-5]。,也可以采用光刻技术或者复制技术[6-8]。不管采用哪种加工方法,都会不可避免地引入一些加工误差,而误差的存在会对衍射光学元件的衍射效率带来直接的影响[9-12],进而导致成像光学系统的像质下降。红外成像光学系统中能够选择的透镜材料种类有限,衍射光学元件的出现为红外系统的设计提供了更多的自由度。致冷型红外系统要能够在一定的温度范围内实行消热差设计,所以系统中采用的衍射光学元件其衍射效率也要进行温度变化的影响分析。
文献[13]讨论了加工误差对衍射光学元件波前像差的影响。文献[10]分析了加工误差对带宽积分平均衍射效率的影响,指出了微结构高度误差是影响衍射效率的重要误差之一。文献[14]给出了环境温度的改变对谐衍射元件衍射效率的影响。文献[15]给出了考虑环境温度因素时多层衍射元件衍射效率的优化方法。本文基于前期工作中给出的微结构高度误差与衍射效率的数学关系,建立了衍射效率和温度与相对微结构高度误差的数学模型。分析了环境温度变化和一定温度范围内工作时,微结构高度误差对衍射效率和带宽积分平均衍射效率的影响。
1 温度与微结构高度误差和衍射效率的理论关系
当入射光线从空气介质正入射到单层衍射光学元件的基底材料上时,衍射光学元件第衍射级次的衍射效率为[11]:
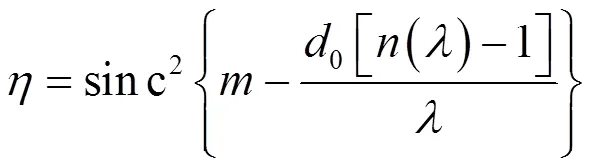
式中:sinc()=sin(p)/p,为衍射级次;0表示衍射光学元件的理论微结构高度的大小;()为元件的基底材料在波长为时对应的折射率。假设由于加工引入的微结构高度误差为D,那么,衍射光学元件的实际微结构高度为:
=0+D=0(1+) (2)
式中:=D/0,表示相对微结构高度误差。考虑微结构高度误差这一因素后,式(1)的衍射效率可以表示为:
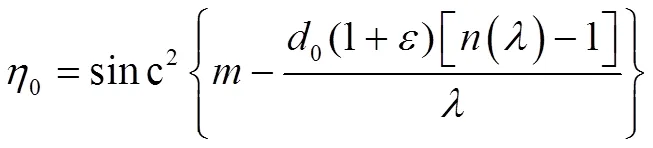
当环境温度变化时,衍射光学元件的微结构高度会随之变化。如图1所示,环境温度的改变会引起衍射光学元件微结构高度大于和小于理论微结构高度。由温度变化导致微结构高度为t,即:
t=0(1+gD) (4)
式中:g=(1/0)d0/d为衍射元件基底材料的热膨胀系数,表示温度变化引起的微结构高度的相对改变量,D为环境温度的变化量,数值上等于环境温度与某一标准温度(一般为20℃)的差值。

图1 温度引起微结构高度改变的示意图
当环境温度变化时,衍射光学元件的微结构高度和基底材料的折射率都会发生改变,进一步引起其衍射效率发生改变。考虑温度这一因素后,衍射光学元件的衍射效率和温度与相对微结构高度误差的关系为:
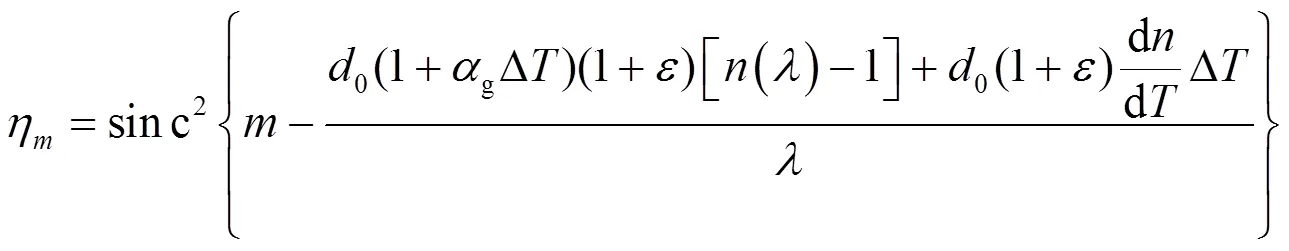
当含有衍射光学元件的混合成像光学系统的工作波段范围为min~max时,需要综合考虑衍射光学元件的带宽积分平均衍射效率,其与温度和相对微结构高度误差的关系为:
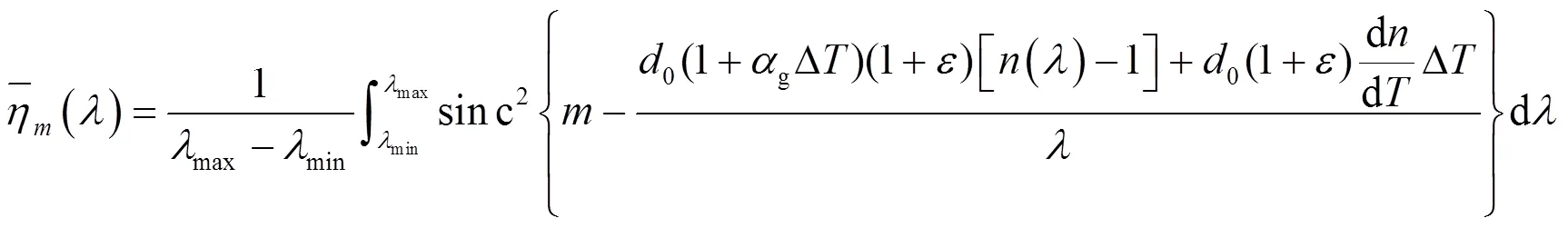
2 分析和讨论
工作在8~12mm波段的衍射光学元件,基底材料采用常用的锗(Ge),衍射级次取=1,根据带宽积分平均衍射效率的最大化计算得到设计波长为0=9.74mm,其微结构高度理论值为0=0/[(0)-1]=3.24mm。
2.1 温度变化对衍射效率的影响
当相对微结构高度误差为零时,根据公式(5),得到衍射光学元件的衍射效率与波长和温度的关系如图2所示。图3给出了在设计波长和边缘波长等几个不同波长处,衍射效率和温度的变化关系。从图中可见,温度从-40℃变化到80℃,在设计波长处,衍射效率变化不大;偏离设计波长越远,衍射效率受温度的影响越大。可以看出高于设计波长的几个波长,如波长为12mm时,衍射效率随温度的降低而减小,随温度的升高而增大;小于设计波长的几个波长,如波长为8mm时,衍射效率随温度的降低而增大,随温度的升高而减小。
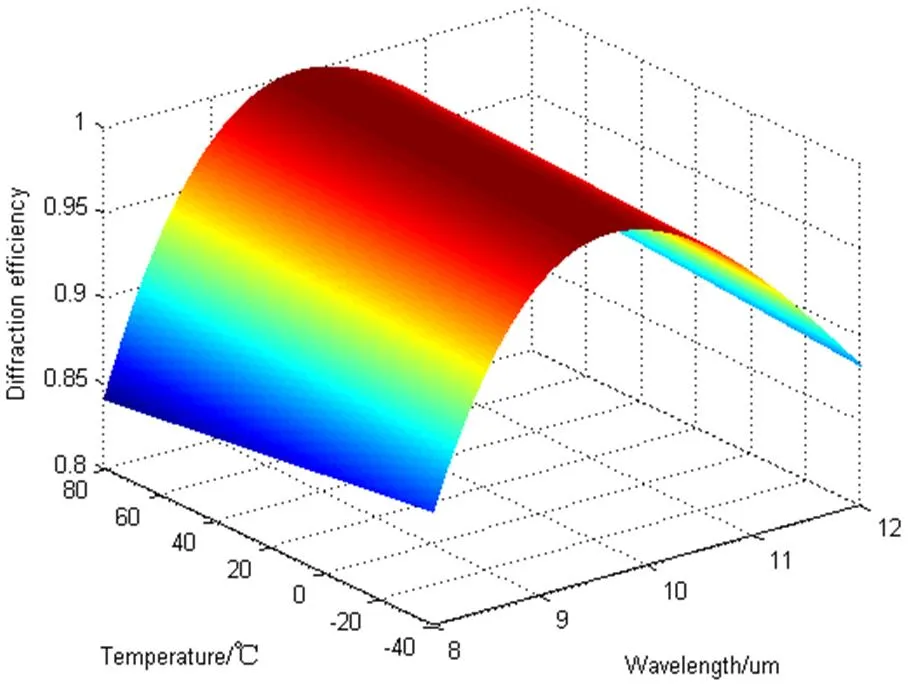
图2 衍射效率与波长和温度的关系
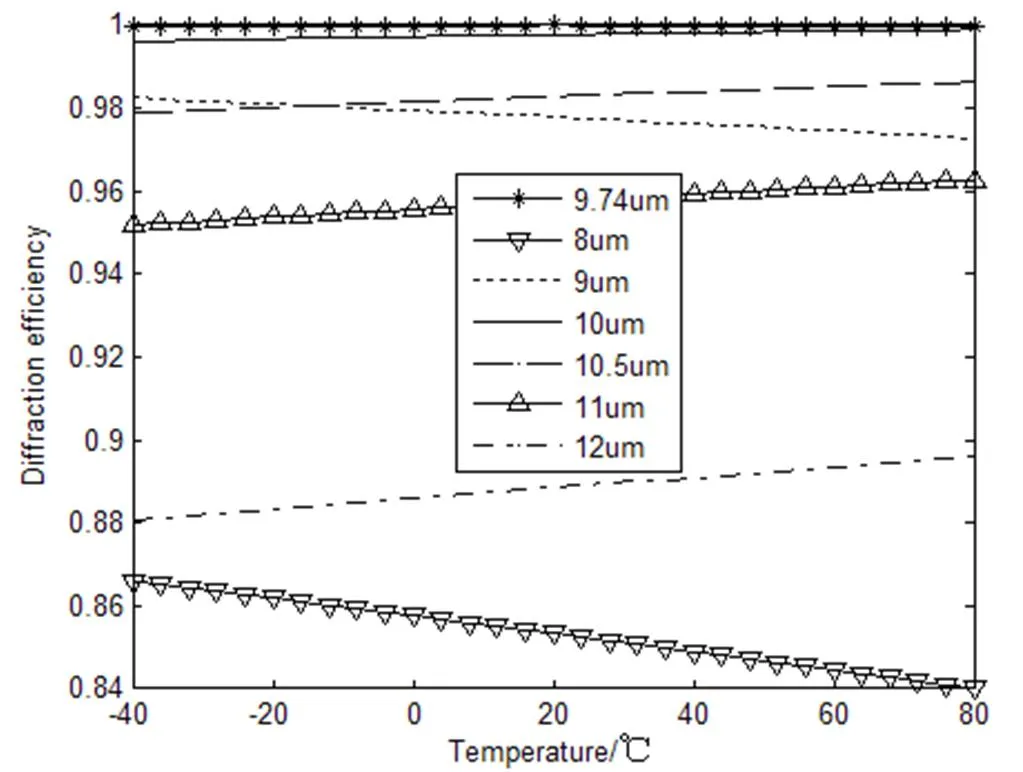
图3 几个不同波长处的衍射效率与温度的关系
Fig.3 Relationship of diffraction efficiency and temperature at several wavelengths
当环境温度为20℃、-40℃和80℃时,衍射光学元件的衍射效率随波长的变化曲线关系如图4所示。温度降低时,实现100%衍射效率的峰值波长向短波移动;温度升高时,实现100%衍射效率的峰值波长向长波移动。所以,在一定温度范围内工作的衍射光学元件,要注意温度变化时所引起的峰值波长改变的现象。根据图3和图4可知在不同温度下对应的衍射效率,当环境温度从20℃升高到80℃时,整个波段范围内的最小衍射效率从20℃时的85.33%下降到为84.02%,下降了1.31%;当环境温度从20℃降低到-40℃时,整个波段范围内的最小衍射效率为86.60%,相比20℃时衍射效率,升高了1.27%。
2.2 温度变化对带宽积分平均衍射效率的影响
当相对微结构高度误差为零,环境温度范围为-40℃~80℃时,根据公式(6)计算得到衍射光学元件的带宽积分平均衍射效率与温度的关系如图5所示。当环境温度从20℃升高到80℃时,或从20℃降低到-40℃时,带宽积分平均衍射效率都是仅下降了0.02%。改变很小。
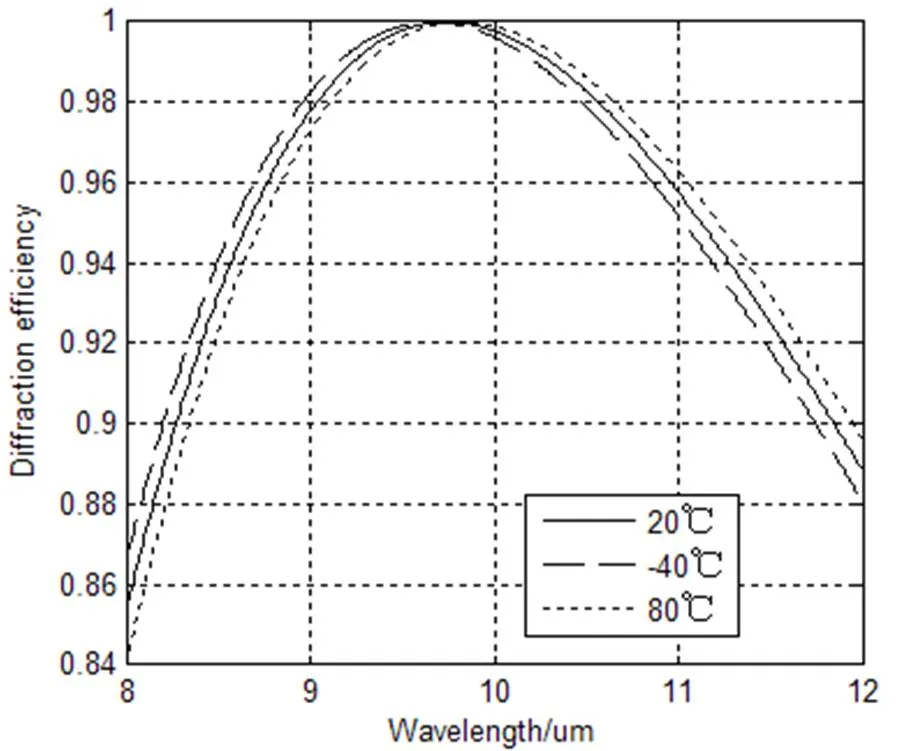
图4 几个不同温度处的衍射效率与波长的关系
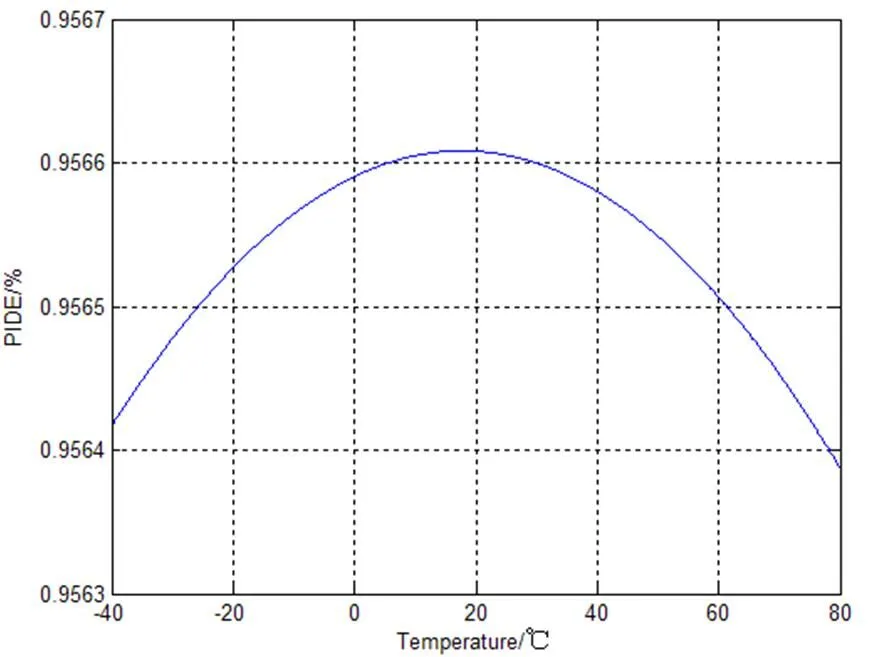
图5 带宽积分平均衍射效率与温度的关系
2.3 温度变化和微结构高度误差对衍射效率的影响
当环境温度为20℃、-40℃和80℃时,利用公式(5)得到衍射光学元件的衍射效率与相对微结构高度误差的关系曲线如图6所示。对比图4,温度降低时,实现100%衍射效率的峰值相对微结构高度误差向正值方向移动;温度升高时,实现100%衍射效率的峰值相对微结构高度误差向负值方向移动。所以,在一定温度范围内工作的衍射光学元件,要注意温度变化时所引起的峰值相对微结构高度误差改变的现象。
当相对微结构高度误差为0、±5%、±10%和±15%时,衍射光学元件的衍射效率与温度的关系曲线如图7所示。可以看出,当衍射光学元件的相对微结构高度误差在±5%范围内时,衍射效率在-40℃到80℃的整个温度范围内高于98.87%;当衍射光学元件的相对微结构高度误差在±10%范围内时,衍射效率在-40℃~80℃的整个温度范围内高于96.13%;当衍射光学元件的相对微结构高度误差在±15%范围内时,衍射效率在-40℃~80℃的整个温度范围内高于91.89%。
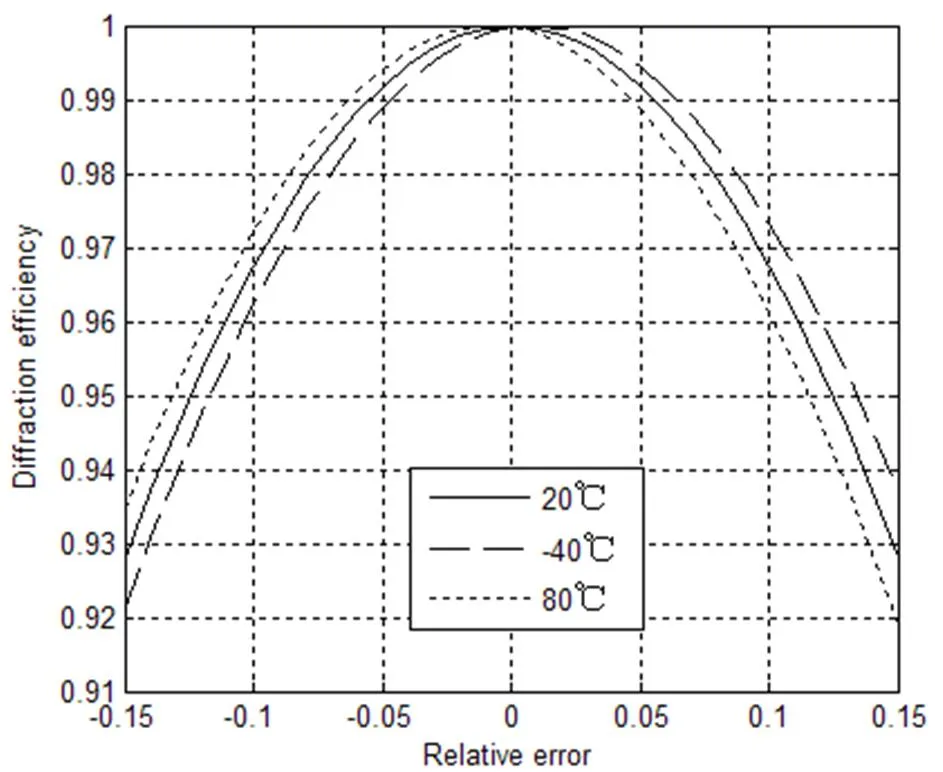
图6 几个不同温度处的衍射效率与相对微结构高度误差的关系
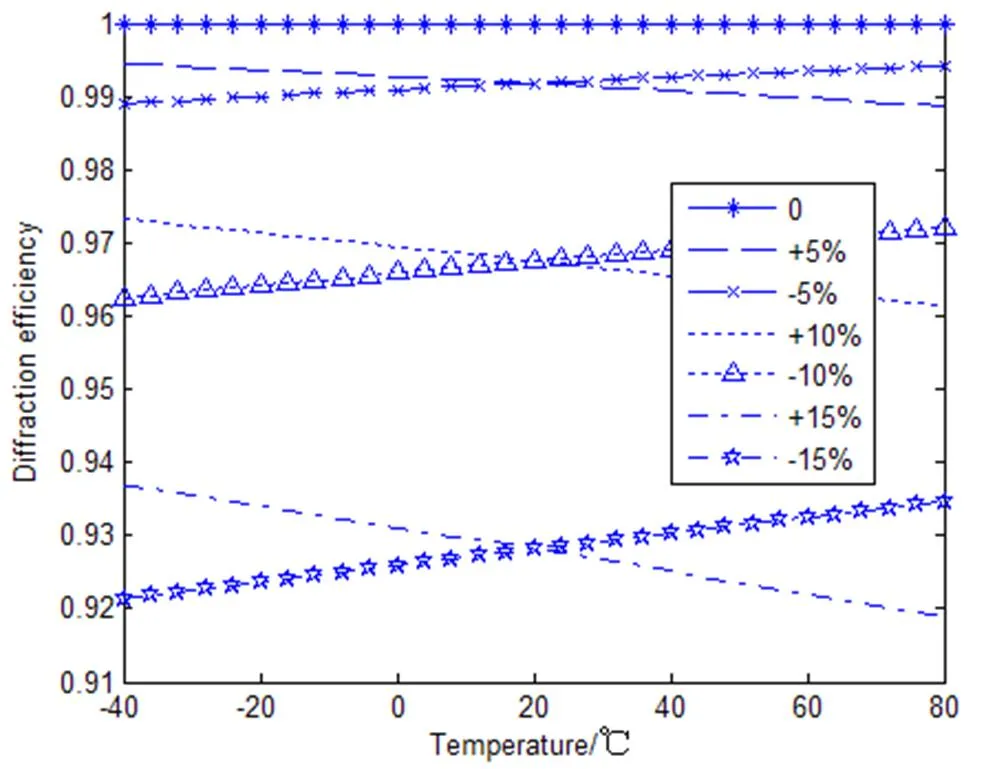
图7 几个不同相对微结构高度误差处的衍射效率与温度的关系
Fig.7 Relationship of diffraction efficiency and temperature at several relative microstructure height errors
2.4 温度变化和微结构高度误差对带宽积分平均衍射效率的影响
当环境温度变化范围为-40℃到80℃时,利用公式(6)计算得到衍射光学元件的带宽积分平均衍射效率与相对微结构高度误差的关系如图8(a)所示。考虑到温度的影响,带宽积分平均衍射效率的最大值为95.65%,此时对应的相对微结构高度误差为-0.04%;当相对微结构高度误差分别为-15%和+15%时,带宽积分平均衍射效率分别为89.19%和89.41%。
当环境温度变化范围相对于20℃不对称时,例如-40℃到40℃时,同理,计算得到衍射光学元件的带宽积分平均衍射效率最大值为95.66%,对应的相对微结构高度误差为0.24%。若环境温度变化范围为-20℃~100℃时,带宽积分平均衍射效率最大值为95.65%,如图8(b)对应的相对微结构高度误差为-0.32%。可见当环境温度不对称时,最大带宽积分平均衍射效率所对应的相对微结构高度误差会有所区别。
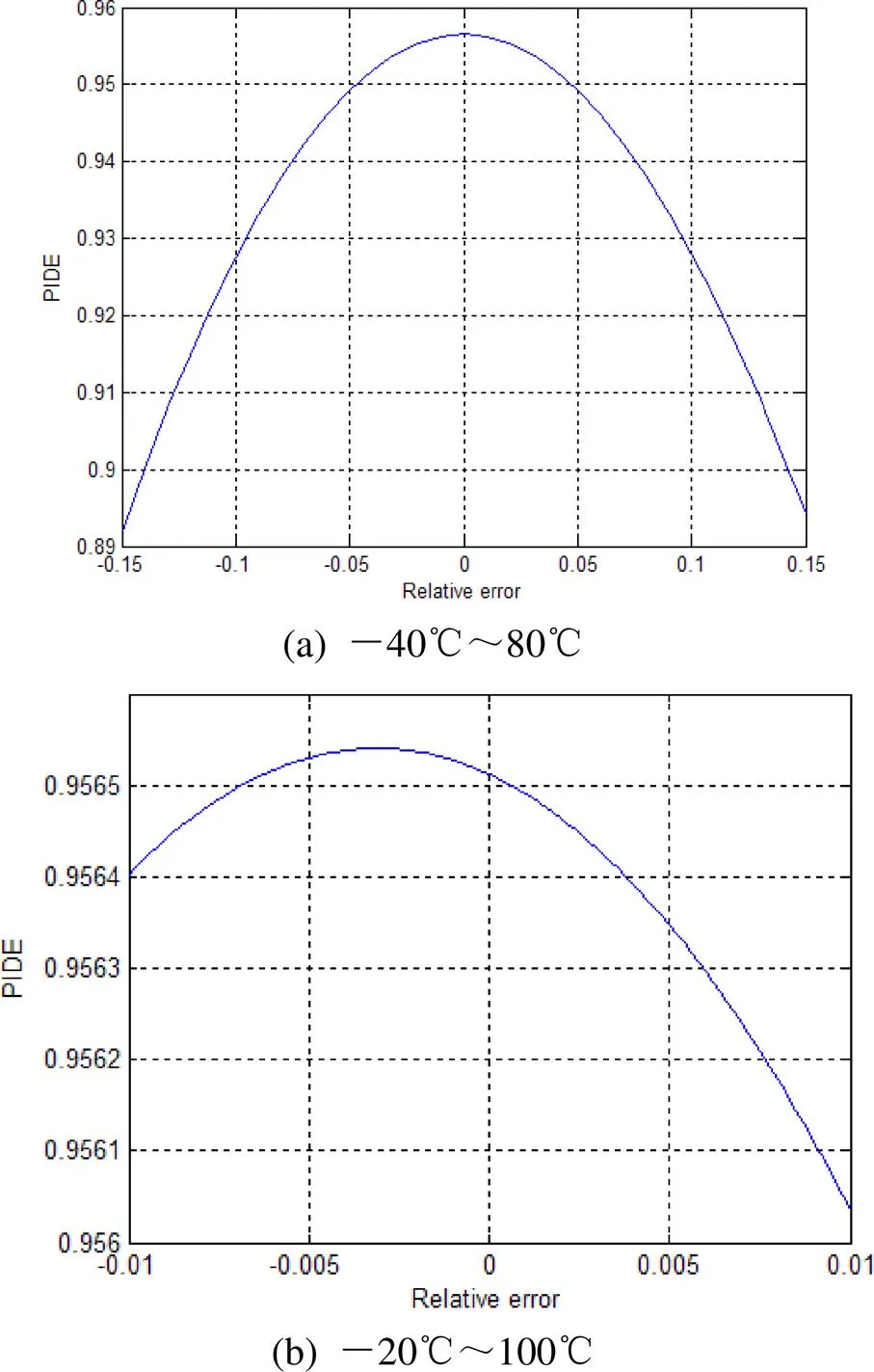
图8 带宽积分平均衍射效率和相对微结构高度误差的关系
当相对微结构高度误差为0、±5%、±10%和±15%时,图9给出了衍射光学元件的带宽积分平均衍射效率与温度的关系。可见,当衍射光学元件的相对微结构高度误差在±5%范围内时,带宽积分平均衍射效率在-40℃到80℃的整个温度范围内高于94.66%;当衍射光学元件的相对微结构高度误差分别在±10%和±15%范围内时,带宽积分平均衍射效率在整个温度范围内分别高于92.28%和88.58%。
3 结论
基于衍射效率与微结构高度误差的表达式,建立了工作在一定环境温度范围内的衍射光学元件的衍射效率与带宽积分平均衍射效率和温度与相对微结构高度误差的数学关系表达式。对于工作中8~12mm长波红外波段的衍射光学元件,偏离设计波长越远,其衍射效率受温度的影响越大。温度的变化会引起100%衍射效率随对应的峰值波长发生改变,也会引起100%衍射效率所对应的峰值相对微结构高度误差偏离理想情况。当衍射光学元件的相对微结构高度误差在±15%范围内时,在-40℃~80℃的整个温度范围内衍射效率高于91.89%,带宽积分平均衍射效率高于88.58%。该分析方法和结论为工作在一定温度范围内的衍射光学元件的设计提供了理论基础。
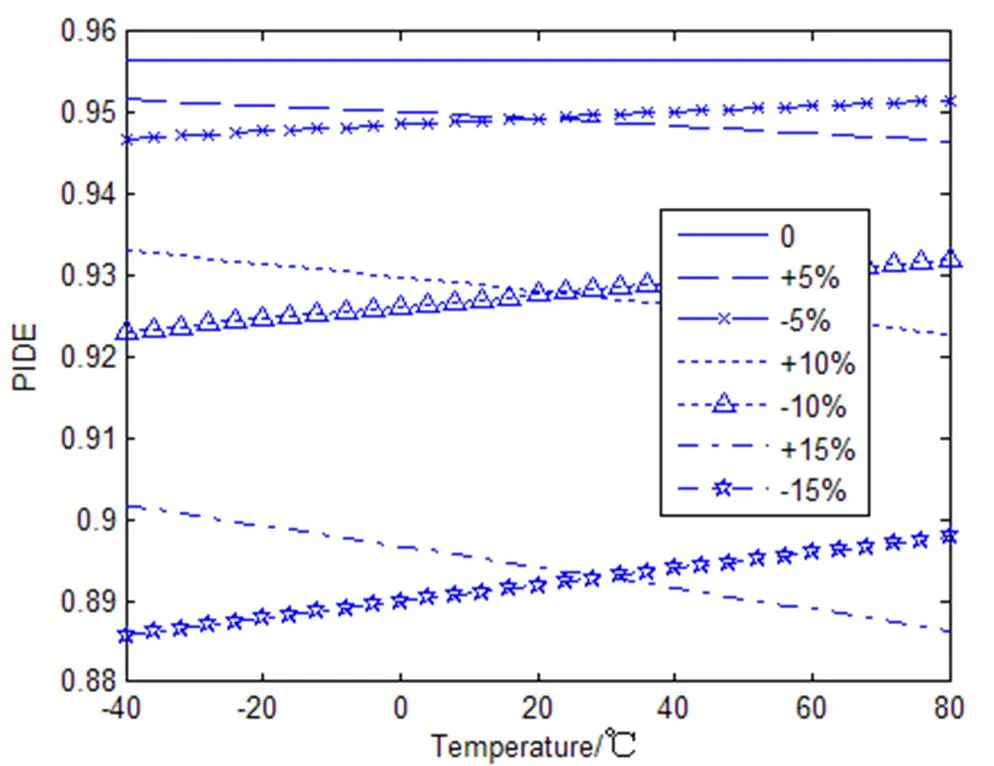
图9 几个相对微结构高度误差处的带宽积分平均衍射效率与温度的关系
Fig.9 Relationship of PIDE between temperature at several relative microstructure height errors
[1] Missig M D, Morris G M. Diffractive optics applied to eyepiece design[J]., 1995, 34(14): 2452-2461.
[2] 刘秀军, 张金旺, 张华卫, 等. 中波红外制冷型光学系统消热差设计[J]. 应用光学, 2013, 34(3): 391-396.
LIU Xiujun, ZHANG Jinwang, ZHANG Huawei, et al. Athermal design of cooled MWIR optical system[J]., 2013, 34(3): 391-396.
[3] 王昊, 康福增, 赵卫, 等. 一种红外双波段衍射望远镜的光学设计[J]. 红外与毫米波学报, 2019, 38(1): 39-43.
WANG Hao, KANG FuZeng, ZHAO Wei, et al. An optical design for dual-band infrared diffractive telescope[J]., 2019, 38(1): 39-43.
[4] Wood A P. A hybrid refractive-diffractive lens for manufacture by diamond turning[J]., 1991, 1573: 122-128.
[5] C Gary Blough, M Rossi, Stephen K Mack, et al. Single-point diamond turning and replication of visible and near-infrared diffractive optical elements[J]., 1997, 36(20): 4848-4654.
[6] Kim Younggwang, Rhee Hyuggyo, Ghim Youngsik, et al. Dual-line fabrication method in direct laser lithography to reduce the manufacturing time of diffractive optics elements[J]., 2017, 25(3): 1636-1645.
[7] Kalima V, Pietarinen J, Siitonen S, et al. Transparent thermoplastics: Replication of diffractive optical elements using micro-injection molding[J]., 2007, 30(2): 285-291.
[8] 程习敏, 白瑜, 谢伟民, 等. 衍射光学元件的加工工艺及其在各种光谱镜头中的应用[J]. 光电技术应用, 2014, 29(2): 31-38.
CHENG Ximin, BAI Yu, XIE Weimin, et al. Fabrication Technology and Application in Spectral Lens of Diffractive Optical Elements[J]., 2014, 29(2): 31-38.
[9] 高龙, 薛常喜, 杨红芳, 等. 偏心误差对长波红外波段多层衍射光学元件衍射效率的影响[J]. 光学学报, 2015, 35(6): 0623004.
GAO Long, XUE Changxi, YANG Hongfang, et al. Effect of Decenter Errors on Diffraction Efficiency of Multilayer Diffractive Optical Elements in Long Infrared Waveband[J]., 2015, 35(6): 0623004.
[10] 毛珊, 崔庆丰. 双层衍射元件加工误差对带宽积分平均衍射效率的影响[J]. 光学学报, 2016, 36(1): 0105001.
MAO Shan, CUI Qingfeng. Effect on Polychromatic Integral Diffraction Efficiency for Two-Layer Diffractive Optics[J]., 2016, 36(1): 0105001.
[11] 杨亮亮, 刘成林, 张志海, 等. 斜入射微结构高度误差的优化设计[J]. 激光与光电子学进展, 2017, 54(6): 060501.
YANG Liangliang, LIU Chenglin, ZHANG Zhihai, et al. Optimal Design of Depth-Scaling Error with Oblique Incidence[J]., 2017, 54(6): 060501.
[12] 杨亮亮. 双层衍射光学元件微结构高度的优化设计[J].红外, 2019, 40(1): 11-15.
YANG Liangliang. Optimal Design of the Microstructure Height for Double-layer Diffractive Optical Elements[J]., 2019, 40(1): 11-15.
[13] Thomas Hessler, Markus Rossi, Rino E Kunz, et al. Analysis and optimization of fabrication of continuous-relief diffractive optical elements[J]., 1998, 37(19): 4069-4079.
[14] 常笑薇. 环境温度变化对双波段谐衍射光学元件衍射效率的影响[J]. 北京交通大学学报, 2016, 40(6): 122-126.
CHANG Xiaowei. Relationship between diffraction efficiency and environment temperature change for double wavebands for harmonic diffractive optics[J]., 2016, 40(6): 122-126.
[15] PIAO Mingxu, CUI Qingfeng, ZHANG Bo, et al. Optimization method of multilayer diffractive optical elements with consideration of ambient temperature[J]., 2018, 57(30): 8861-8869.
Research on the Influence of Temperature and Microstructure Height Error on Diffraction Efficiency for Diffractive Optical Elements
YANG Liangliang,ZHAO Yongbing,TANG Jian,GUO Renjia
(School of Physics and Electronics Engineering, Yancheng Teachers University, Yancheng 224007, China)
Based on the relationship between diffraction efficiency and microstructure height error for diffractive optical elements (DOEs), mathematical analytical models of environment temperature, microstructure height error, and diffraction efficiency/polychromatic integral diffraction efficiency (PIDE) were put forward. The influence of ambient temperature on the PIDE was researched and the relationship between the PIDE and microstructure height error within a certain temperature range was analyzed. For a DOE working within an 8-12mm long-waveband infrared range, the influence of temperature on the diffraction efficiency was significant as the wavelength deviated from the designed value. The peak relative microstructure height error corresponding to the 100% diffraction efficiency changed with the change of temperature. When the relative microstructure height error of the DOE was within ±15%, the diffraction efficiency was higher than 91.89% in the temperature range from -40℃ to 80℃ and the PIDE was higher than 88.58% in the entire temperature range.
diffractive optics, diffraction efficiency, microstructure height error
O436
A
1001-8891(2020)05-0213-05
2019-07-22;
2019-12-20.
杨亮亮(1986-),女,副教授,博士,主要从事衍射光学、光学设计和聚光光伏系统等方面的研究。E-mail:yang_liangliang@163.com。
江苏省高校自然科学研究项目(19KJD140005),国家自然科学基金(11847161,11847166)。

