双轨火箭橇全时程动力学仿真分析研究

顾凯旋，龚明生，王磊，熊闯

(1.航空工业航宇救生装备有限公司 试验部，襄阳 441003) (2.北京航空航天大学 固体力学研究所，北京 100143)

0 引 言

火箭橇是在专用的轨道上，推动滑车高速前进以获取模型试验测试数据的大型地面动态试验系统。由于这种试验技术能够模拟飞行状态，已成为现代武器所有地面试验设备中比较有效的一种特殊试验手段[1-3]，可以解决飞机、导弹、宇航飞行器及其他武器或机械设计在研制过程中有关高速度、高加速度可能带来的许多技术问题。然而火箭橇的振动问题，往往过载都超过500g，这对于试验的准确性和安全性都有较大的影响[4-5]。因此，研究火箭橇的振动问题具有理论意义和实用价值。

双轨火箭橇在载重方面优于单轨火箭橇，但是双轨火箭橇由于轨道不平顺所引起姿态振动的理论分析研究工作也远远要复杂于单轨火箭橇。当前针对火箭橇动力学响应的研究正处于起步阶段，S.I.Gerasimov等[6]对橇轨之间的橇轨接触变形及运动稳定性进行了分析；D.J.Laird等[7-8]对高速火箭橇滑靴-滑轨撞击过程进行了仿真分析，并建立了二维平面下滑靴-滑轨的交互耦合模型；J.H.Zhang等[9]对火箭橇刚柔耦合模型的动力学分析进行了研究。相比而言，国外动力学分析方法较为成熟且发展了相应的分析软件，而国内目前针对火箭橇动力学分析的理论还不完善。王健等[10]对火箭橇轨道不平顺功率谱密度进行了分析；董治华等[11]对火箭橇减振系统进行了分析；杨珍等[12]对单轨火箭橇的载荷预示技术进行了研究；张雨诗等[13]对火箭橇轨道系统有限元建模及振动特性进行了研究。然而以上研究均是对火箭橇系统的各个子模块进行了研究，针对火箭橇系统的动力学分析理论仍然匮乏，尤其是针对双轨火箭橇，关于其动力学分析的研究鲜有报道。系统地研究双轨火箭橇振动行为，分析其在试验各时刻的振动响应，是火箭橇理论研究与试验领域亟待解决的重大问题。

本文针对双轨火箭橇系统，建立橇轨-滑车系统的动力学分析模型。首先对真实模型进行模态分析，通过优化方法，采用梁单元建立橇车三维实体模型的简化模型。在此基础上，推导综合考虑阻尼、橇轨间隙以及不平顺度的火箭橇运动动力学方程并进行求解。在已有的研究经验基础上，以期进一步丰富火箭橇动力学分析理论。

1 滑车模型简化

滑车模型复杂，动力学计算规模巨大。在分析时需要对其进行必要的模型简化，在保证模型动力学特性基本不变的前提下，降低模型的复杂程度，从而提升计算效率。

根据滑车的模型图，对其进行网格划分，得到滑车有限元模型如图1所示。根据其几何特征，得到其简化模型如图2所示，其中，各部分均采用梁单元来模拟。

图1 双轨火箭橇滑车有限元网格模型Fig.1 Finite element model of two-track rocket sled

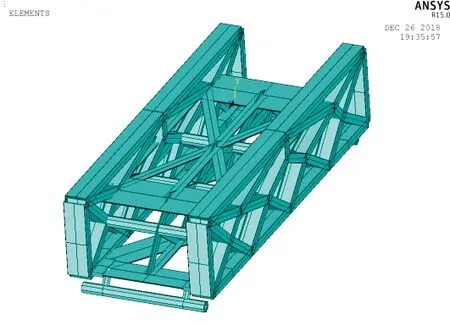
图2 双轨火箭橇简化模型Fig.2 Simplified model of two-track rocket sled

对简化模型进行修正，得到简化模型与真实模型前5阶频率对比如表1所示。简化模型与真实模型前5阶模态振型也基本一致，因此，对模型的简化取得了较好的效果。

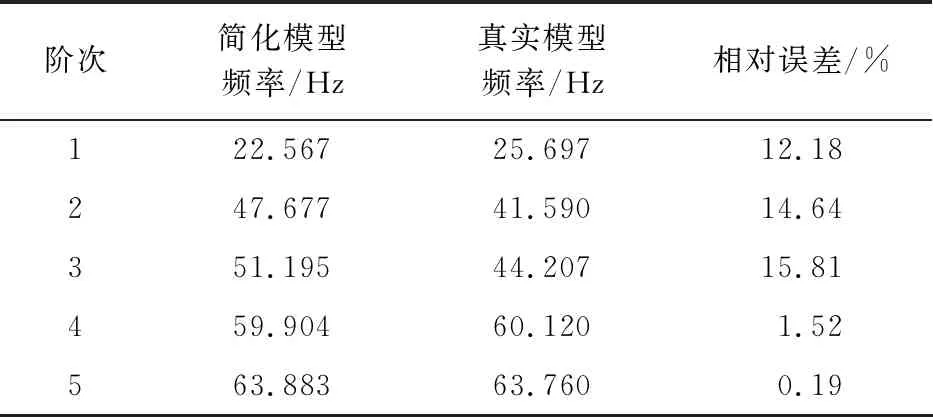
表1 简化模型与真实模型频率对比

2 动力学计算分析

2.1 计算输入

由于火箭橇-滑车的振动主要为垂向及侧向的振动。对于航向，火箭橇存在大范围刚体运动与小量级的结构振动，小量级振动变形较小且不影响关注问题的结果，故可忽略，因此可将火箭橇的航向运动简化为刚体运动。根据实测数据得到滑车航向速度曲线如图3所示。

图3 航向速度曲线Fig.3 Curve of course speed

根据测点位置对轨道不平顺值进行测量，对于不平顺表达的输入参数只需获得实际的轨道不平顺值与监测点间隔。根据轨道不平顺数据能够得到任意位置轨道的不平顺值及其斜率。轨道不平顺值d的计算公式和轨道不平顺斜率kd的计算公式分别为

(1)

kd=d/l1

(2)

式中：dn+1为当前滑块位置后一个轨道监测点的不平顺监测值；dn为当前滑块位置轨道前一个监测点的不平顺监测值；l1为当前滑块位置距离前一个观测点的长度；L为监测点间隔长度。

2.2 橇-轨碰撞接触力计算

在火箭橇动力学仿真中，采用L-N非线性接触力模型计算轨道与橇车滑块之间的橇-轨接触力。L-N非线性接触力模型可写为如式(3)所示：

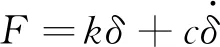
(3)

橇-轨碰撞接触力求解流程如图4所示，接触力计算流程如下：

(1) 由橇车的航向运动确定当前时刻橇车各滑块在轨道中的位置和橇车的运动速度；

(2) 由滑块当前位置确定轨道不平顺值和不平顺斜率，进而确定橇车滑块与轨道接触状态；

(3) 由上述步骤判断得出接触变形和接触变形速率，调用式(3)所示的接触力模型即可计算当前时刻的橇-轨碰撞接触力。

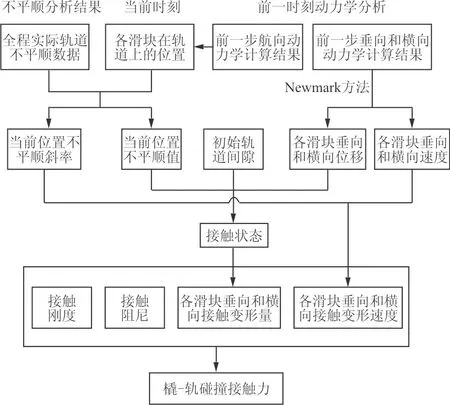
图4 橇-轨碰撞接触力求解流程Fig.4 Flowchart of solution of skid-rail collision contact

2.3 动力学仿真计算方法

综合考虑橇车的垂向振动、横向振动和航向刚体运动，火箭橇的振动的有限元方程可写为

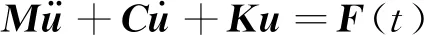
(4)

阻尼矩阵C采用瑞利阻尼模型，即：

C=αM+βK

(5)

式中：α及β的取值根据文献[14]所给方法求得；简化模型的总体质量矩阵M和刚度矩阵K利用ANSYS提取。

(6)

(7)

式中：γ和δ是按积分精度和稳定性要求决定的参数。

当γ=1/4和δ=1/2时，Newmark方法退化为常平均加速度法这样一种无条件稳定的积分方案。此时，Δt内的加速度为

(8)

Newmark方法中的时间t+Δt的位移ut+Δt是通过满足时间t+Δt的运动方程得到的。

从公式(7)可得：

(9)

根据

(10)

(11)

全时程动力学求解流程如图5所示，求解步骤为：

(1) 初始化计算，设定计算总时间T，计算时间步长Δt。设置当前时间步为t=0(即初始时刻)，获取航向运动初始位置、速度和加速度，垂向和横向运动初始位置、速度和加速度。

(2) 由t时刻航向运动得到航向的位移，速度与加速度。

(3) 由t时刻滑块的航向位置，结合轨道不平顺值和不平顺斜率，得到当前的接触变形与接触变形速率。通过调用橇-轨碰撞接触力计算模块，判断滑车各个滑块与轨道的碰撞接触情况并计算当前时刻垂向和横向的橇-轨碰撞接触力。

(4) 由当前运行时间t、橇车航向速度以及橇-轨碰撞接触力确定橇车当前时间步的其他各项外载荷输入条件。

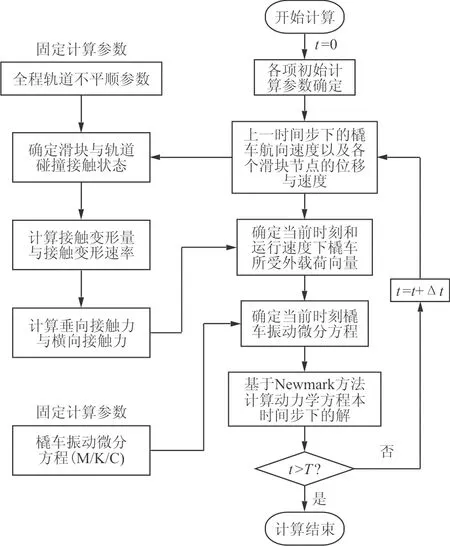
图5 动力学仿真计算流程Fig.5 Flowchart of the dynamics simulation calculation

(5) 通过调用Newmark数值积分方法求解橇车动力学方程(即式(5))，得到t+Δt时刻橇车的垂向和横向位移、速度以及加速度响应。

(6) 令t=t+Δt，判断t是否大于总时间T，若t≤T，则返回步骤(2)继续进行动力学仿真计算，否则结束计算。

2.4 动力学计算结果

取航向速度最大段结果进行分析，本文仅给出了其中一个滑块的结果，其余三个滑块的结果基本相同。滑块处垂向碰撞接触力、垂向过载及功率谱密度曲线如图6～图8所示。

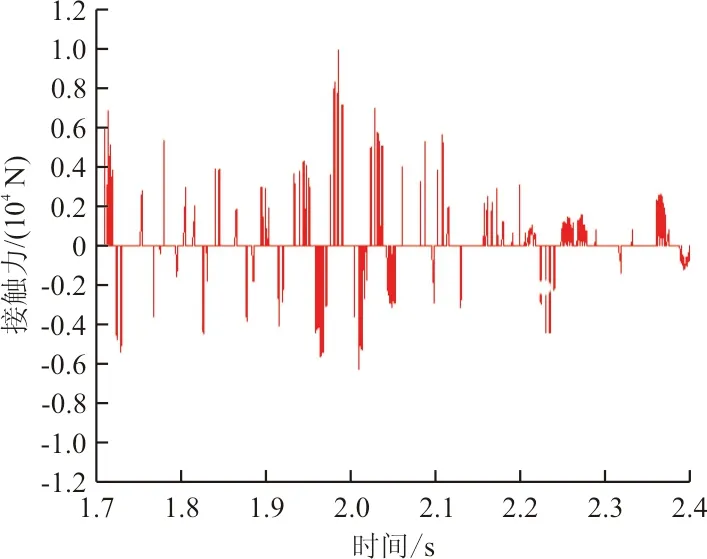
图6 碰撞接触力曲线Fig.6 The curve of the collision contact force

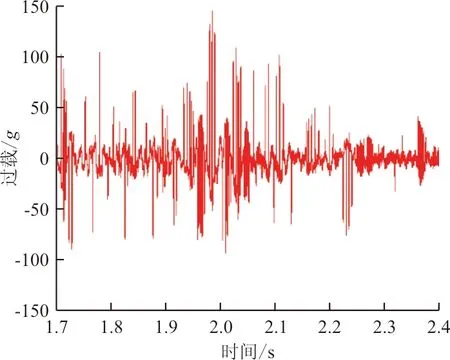
图7 滑块垂向过载曲线Fig.7 Vertical overload curve of the slider

图8 滑块垂向加速度功率谱密度曲线Fig.8 Vertical acceleration power spectral density curve of the slider

由于本文所计算的车体未进行试验，采用速度基本相同的火箭橇振动响应的试验结果进行了对比，试验数据如表2所示。

表2 火箭橇试验振动响应结果

从上述结果可以得到以下结论：

(1) 滑块处过载曲线峰值出现在滑车运行速度较大的时刻。由于滑车速度快，单位时间内滑靴所经历的轨道不平顺变化较大，使得滑靴与轨道的碰撞接触力增大。因此随着滑块航向速度的增大，过载也变大。其峰值过载为140g，与速度基本相同的火箭橇试验实测得到的130g基本吻合，说明计算所得的数据有一定的可信性。

(2) 各测点振动能量主要集中在0～800 Hz，1 000 Hz以后振动非常微弱，与速度基本相同的火箭橇试验实测结果基本一致，验证了本文所提出方法的正确性。

3 结 论

(1) 本文采用梁单元对真实模型进行了简化，通过对比简化模型与真实模型的前5阶频率及模态振型，表明简化模型复杂度低，计算效率高。

(2) 推导了考虑阻尼、橇轨间隙以及不平顺度的火箭橇运动动力学方程组，并通过数值方法对双轨火箭橇系统进行了全时程动力学响应求解。仿真分析结果与速度基本相同的火箭橇试验实测结果基本吻合，验证了本文采用的仿真分析方法的合理性。

本文所采用的仿真分析方法可用于试验前对双轨火箭橇进行动力学分析，对试验结果有提前的预判。在计算中模型简化以及计算参数的设定会带来计算误差，因此，该仿真分析方法仅仅能得到一个量级正确的粗略结果，要得到火箭橇系统精确的动力学响应，还是要借助试验。