基于Hyperlynx的高速电路端接技术仿真研究

王祎帆 王杨 王强 赵目龙 赵晓雪

（中国第一汽车股份有限公司 智能网联开发院，汽车振动噪声与安全控制综合技术国家重点实验室，长春130013）

主题词：高速电路 端接 Hyperlynx 信号完整性 反射 仿真

1 前言

随着汽车智能化、网联化的发展，DDR4（Double Data Rate 4th-generation Synchronous Dynamic Random-access Memory）等高速存储芯片在汽车电子中的应用越来越广泛，高速化、小型化成为现阶段智能网联类控制器的设计趋势。与此同时，信号频率的提高、印刷电路板（Printed Circuit Board，PCB）尺寸的减小、PCB叠层的增加，都会对信号的质量产生影响[1-5]。通常认为，当信号频率高于100 MHz，或者信号的传输延迟大于10%的信号上升沿的时长情况下，该电路就属于高速电路[6-8]。此时，就需要用高速电路的设计理念去设计电路原理图和PCB。否则，控制器可能会由于信号完整性的问题导致无法正常工作。

采用端接技术、降低信号频率、缩短PCB走线，都可有效地抑制反射现象[9-10]，但由于控制器功能的要求和PCB尺寸的限制，后2种方式很难在实际工程中得到应用。端接技术是现阶段在高速电路设计中最常使用的方案。

本研究首先针对于反射的形成机理进行理论分析，推导反射系数的公式。在此基础之上，引出6种常见的端接方式，并对这6种方式进行详细讨论。最后，通过仿真分析、验证了端接对于反射的抑制效果，除此之外，还对不同端接方式中端接参数的选取进行了探讨。

2 反射的形成机理

2.1 传输线模型

当信号的互连尺寸远小于信号最高频率所对应的波长时，信号线可以用集总模型进行分析，此时信号从输出端口到输入端口的传递是没有延迟的。当信号的互连尺寸与信号最高频率所对应的波长可以比较时，通常采用分布模型进行分析，这里的分布模型是集总模型的串联[11]。

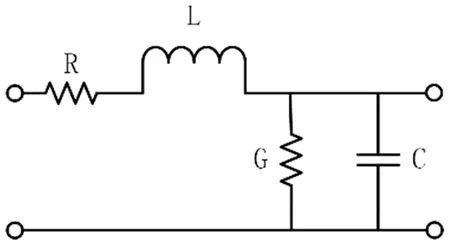
图1 传输线单位长度的等效电路

图1为单端口网络单位长度的集总模型示意图，其中R为传输线的分布电阻，L为传输线的分布电感，G为传输线的分布电导，C为传输线的分布电容，上述参数都为传输线的寄生参数。通常将这个模型称为传输线的RLGC模型。

2.2 特征阻抗

通常，将传输线输入电压与输入电流的比值定义为传输线的特征阻抗Z0，其中：

式（1）中，Ui(z)为传输线的输入电压，Ii(z)为传输线的输入电流。

从图1的集总模型示意图可以推导出特征阻抗的公式：

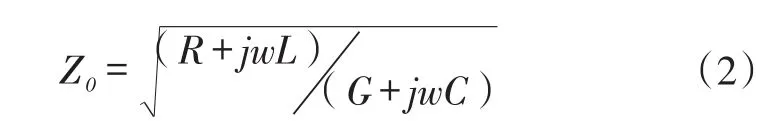
式（2）中，w=2πf，其中f为信号的频率。

当信号频率很高，例如大于100 MHz时，jwL和jwC的数值要远大于R和G的数值，所以公式（2）可以简化为：

从公式（3）中可以看出，理想传输线的特征阻抗仅与传输线的分布电感L和分布电容C有关，与传输线上的信号频率和传输线的长度无关。

2.3 反射系数

从上一小节了解到，理想传输线的特征阻抗与分布电感L和分布电容C有关，而分布电感和分布电容是由走线的宽度、介质层的介电常数、介质层厚度、走线到参考平面距离参数决定。所以，在实际PCB上布线时，由于过孔、PCB板材不均匀的原因，会导致传输线的特征阻抗发生变化。信号在传输线特征阻抗变化的点会发生反射。通常，将信号的反射系数ρ0定义为[12]：

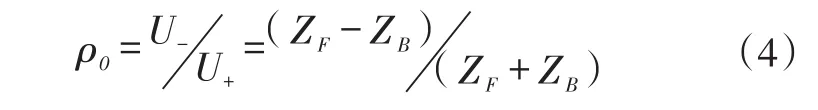
式（4）中，U-为反射点处的反射电压，U+为反射点处的入射电压，ZB为反射点后的传输线特征阻抗，ZF为反射点前的特征阻抗。

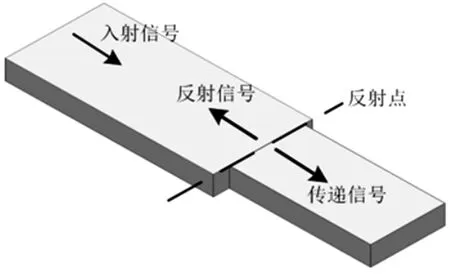
图2 信号反射示意

图2是信号发生反射的一种特例，即PCB走线宽度发生变化，从而导致传输线特征阻抗变化，信号在反射点位置发生反射。一部分能量沿着信号方向接着传递，一部分能量沿信号反方向返回源端。

当反射点前特征阻抗ZF等于反射点后特征阻抗ZB时，能量不会发生反射，此时反射系数ρ0为0。当反射点前特征阻抗ZF远大于反射点后特征阻抗ZB时，此时走线相当于短路，反射系数为1。当反射点前特征阻抗ZF远小于反射点后特征阻抗ZB时，此时走线相当于开路，反射系数为-1。

3 端接技术仿真分析

从上面的分析可以得出，要想从根本上抑制反射，就要保证在信号的传递路径上，各点的反射系数都必须为0。有2种端接方式在实际工程中得到了广泛的应用，分别是串联端接和并联端接，其中并联端接又包含简单并联端接、主动并行端接、戴维南端接、阻容端接、二极管端接5种形式。

3.1 串联端接

串联端接就是在尽可能靠近信号输出端口的位置串接一个电阻，使得信号源输出阻抗Zout加上串接电阻RS的阻抗ZS等于传输线的特征阻抗Z0，如图3所示。当传输线上只有一个负载时，这种端接方式得到了广泛的应用。但是由于传输线特征阻抗Z0与信号接收端的输入阻抗Zin不匹配，所以信号还是会在接收端发生反射，产生振铃、过冲、下冲现象。综上，串联端接并不能消除信号的一次反射，而是消除信号的二次反射。除此之外，由于串接的电阻会增加信号的RC时间参数，所以在高频领域，不建议使用这种端接方式。

图3 串联端接示意

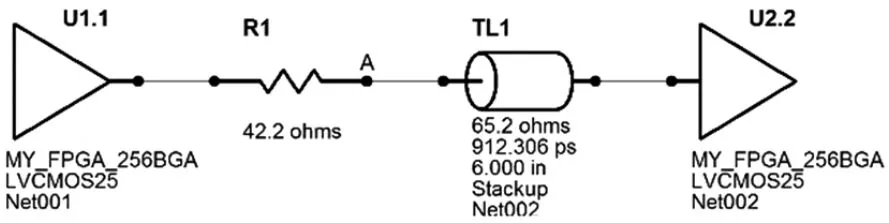
图4 串联端接仿真示意

图5 不同串联电阻下的信号波形

图4为串联端接在Hyperlynx软件中的示意图，其中U1.1为输出缓冲器，R1为串联电阻，TL1为传输线，U2.2为输入缓冲器。仿真中，将TL1定义为长度152.4 mm，宽度0.127 mm(5 mils)的顶层（TOP层）走线。可以从图4中看到，该段传输线的特征阻抗为65.2 Ω，传输延迟为912.306×10-12s（912.306 ps）。

从图5中可以看到，随着时间的推移，不论串联电阻的阻值为多少，输出端和接收端的电压都将稳定在2.5 V。另外，信号在传输线上的传递时间也与串接电阻的阻值无关。当串接电阻R1的阻抗为0 Ω时，信号的过冲和下冲最为明显。当串接电阻R1的阻抗为80 Ω时，信号的输出电压不足，并且信号的上升速度最慢，以上2种情况在实际的工程应用中都应该避免。当串接电阻R1的阻抗为42.2 Ω时，信号波形传递良好，过冲较小，说明信号的反射现象被有效地抑制。

当串接电阻R1的阻抗为0 Ω时，根据公式（5）可以得到U1.1的第一个平台电压为1.94 V，仿真结果为1.95 V。另外，输入缓冲器的输入阻抗通常很大，近乎于断路，根据公式（4）可以得出此时的反射系数为1，那么相应的输入端U2.2的电压应该为输出端U1.1电压的2倍，仿真测得的电压为3.85 V，与计算结果相符。

式（5）中，Z1为串联电阻的阻抗，Z0为传输线的特征阻抗（在本例中为65.2 Ω），ZOUT为输出缓冲器的输出阻抗，V1.1为图4中的A点电压，VOUT为输出缓冲器的输出电压。

3.2 简单并联端接

简单并联端接就是在靠近信号输入端口的位置并联一个对地电阻，该并联电阻RP的阻抗ZP等于传输线的特征阻抗Z0，如图6所示。由上文可知，串联端接消除的是信号的二次反射。而简单并联端接消除的是信号的一次反射，所以可以有效地减小信号噪声。并且在多负载情况下，工作性能良好。除此之外，简单并联端接具有使用器件少、电阻阻抗值容易确定等优点。但是由于并联电阻RP的存在，会引入一个到地（GND）的直流通路，所以信号线上的直流功耗会增加。

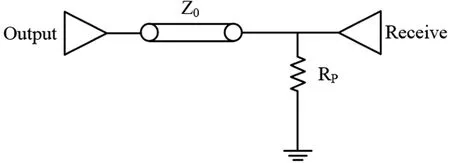
图6 简单并联端接示意

图7 简单并联端接仿真示意

图7为简单并联端接在Hyperlynx软件中的示意图，其中U3.3为输出缓冲器，R2为并联电阻，TL2为传输线，U4.4为输入缓冲器。

图8 简单并联端接信号波形

图8为简单并联端接的信号波形，从图中可以看到，随着并联电阻阻抗的增大，接收端的稳定电压逐渐提高。根据公式（6）可得稳定电压的具体数值。

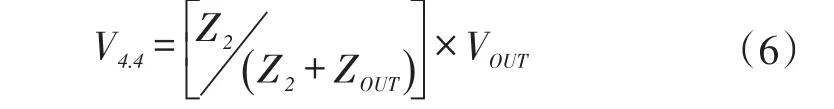
式（6）中，Z2为并联电阻的阻抗，ZOUT为输出缓冲器的输出阻抗，VOUT为输出缓冲器的输出电压。

从图8可以看到，当并联电阻R2的阻抗为65.2 Ω时，此时并联电阻阻抗等于传输线的特征阻抗，信号的过冲和下冲最小。但是由于并联电阻R2的存在，会降低接收端的稳定电压，并联电阻阻抗越小，接收端稳定电压越低，信号的抗噪声能力越弱。若不能选取合适的并联电阻，甚至可能导致接收端的稳定电压低于接收端的高电平阈值，从而导致接收端无法获取正确的信号。当并联电阻的阻抗等于传输线的特征阻抗时，信号的稳定电压由输出缓冲器的输出阻抗决定，若输出缓冲器输出阻抗过大，接收端的稳定电压同样可能低于接收端的高电平阈值，即输出缓冲器的驱动能力不够。

3.3 主动并行端接

为了解决简单并联端接会降低接收端信号稳定电压的问题，可以采用主动并行端接的方案。主动并行端接，即在信号输入端口位置并联一个上拉到Vpullup的电阻RU，如图9所示。该方案要求上拉电阻RU的阻抗等于传输线的特征阻抗，并且上拉电压源应具备吸、灌电流的能力，用以满足输出电压跳变速度的要求[13]。主动并行端接同样可以消除信号的一次反射，但是由于输出缓冲器内阻ZOUT的存在，信号线的低电平会被抬高。主动并联端接的应用场景非常广泛，DDR4地址和命令线上即采用了这种端接方案。

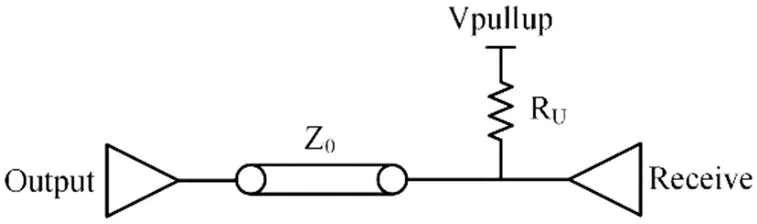
图9 主动并行端接示意

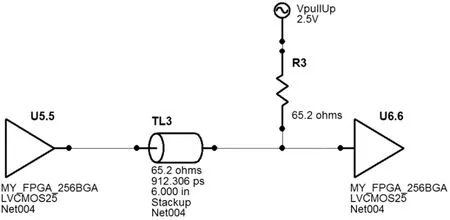
图10 主动并行端接仿真示意

图10为主动并行端接在Hyperlynx软件中的示意图，其中U5.5为输出缓冲器，R3为上拉电阻，TL3为传输线，U6.6为输入缓冲器，上拉电压Vpullup为2.5 V。

图11 不同阻抗的R3下，主动并行端接信号波形

从图11中可以看到，当上拉电压Vpullup为2.5 V时，不论上拉电阻R3的阻抗为多少，接收端的信号稳定电压都为2.5 V。主动并行端接要求上拉电阻的阻抗等于传输线的特征阻抗，仿真结果表明，当上拉电阻的阻抗为65.2 Ω时，接收端的信号最为理想，理论与仿真结果一致。另外，随着上拉电阻阻抗的减小，信号线的低电平被逐渐抬高，这是由公式（7）所决定。

式（7）中，Z3为上拉电阻的阻抗，ZOUT为输出缓冲器的输出阻抗，VOUT为输出缓冲器的输出电压，Vpullup为上拉电压。

当输出缓冲器的输出电压为0 V时，公式（7）可以简化为：

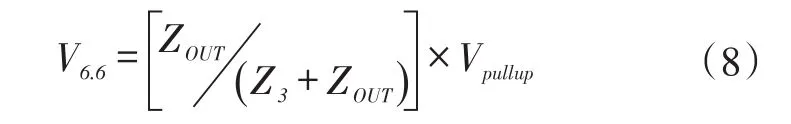
根据公式（8）可得，当上拉电阻的阻抗为65.2 Ω时，接收端电压应为0.55 V，仿真结果为0.53 V，计算与仿真结果相吻合。

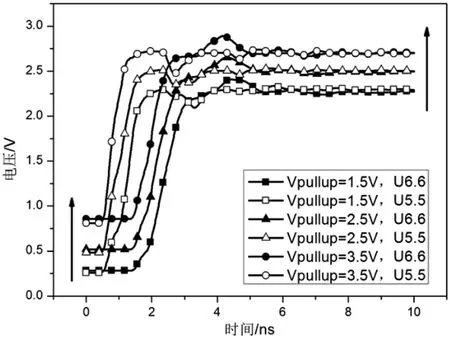
图12 不同Vpullup下，主动并行端接信号波形

从图12中可以看到，当上拉电阻R3的阻抗为65.2 Ω时，随着Vpullup的增大，信号线上的低电平被不断拉高。同时，接收端信号的稳态电压也逐步增大。但是上拉电压Vpullup的大小，并不会对信号的上升时间产生影响。而且，信号过冲和下冲的幅值也与Vpullup的大小几乎无关。若Vpullup的上拉电压数值选取不合适，可能会导致信号线上的低电平数值一直高于输入缓冲器的低电平阈值，从而导致系统设计错误。

3.4 戴维南端接

针对于上述两个小节的讨论，可知简单并联端接和主动并行端接都可以消除信号的一次反射，有效地降低信号的过冲和下冲，但是简单并联端接会拉低接收端的高电平电压，主动并行端接会抬高接收端的低电平电压。在某些驱动能力较弱的电路中，上述两种端接方法并不适用。为了解决这些问题，可以采用戴维南端接的方案。戴维南端接，即在信号输入端口位置并联一个上拉到Vpullup的电阻RU和一个下拉到地的电阻RD，如图13所示。这种端接方法要求上拉电阻RU和下拉电阻RD的并联阻抗等于传输线的特征阻抗。但是由于RU和RD的存在，该端接方案会增加信号线上的直流功耗。

图13 戴维南端接示意

图14 戴维南端接仿真示意

图14为戴维南端接在Hyperlynx软件中的示意图，其中U7.7为输出缓冲器，R4为上拉电阻，R5为下拉电阻，TL4为传输线，U8.8为输入缓冲器，上拉电压Vpullup为2.5 V。

从图15中可以看到，戴维南端接波形处于简单并联端接和主动并行端接波形之间。在实际工程应用中，通过选择合适的R4和R5，可以使得信号的高低电平满足设计要求。同时，电阻R4和R5具有限流的作用，为避免驱动电流和直流功耗过大，其阻抗值不应过小。上拉电阻R4的最大数值由信号的最大上升时间决定，最小数值由输出缓冲器的最大灌电流决定。与简单并联端接和主动并行端接相比，戴维南端接使用了2个电阻，在高密度PCB的设计中，这样的端接方案会增加PCB的设计难度。

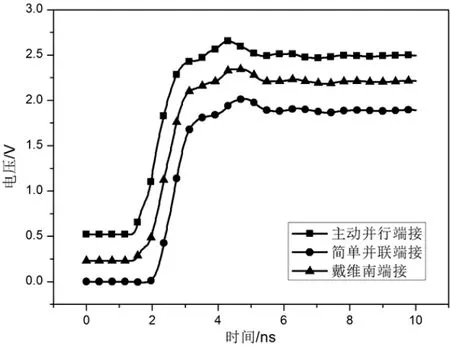
图15 三种端接方式的信号波形对比

3.5 阻容端接

为了解决并联端接引起的直流功耗大的问题，可以采用阻容端接的方案。阻容端接，即在信号输入端口位置并联一个电阻RD和一个对地的电容CD，如图16所示。由于对地电容CD隔绝直流的能力，采用这种端接方案可以有效地减小电路直流功耗。阻容端接要求电阻RD的阻抗小于等于传输线的特征阻抗，对地电容CD为：

式（9）中，TR为信号的上升时间，Z0为传输线的特征阻抗。

图16 阻容端接示意

图17为阻容端接在Hyperlynx软件中的示意图，其中U9.9为输出缓冲器，R6为下拉电阻，C1为对地电容，TL5为传输线，U10.10为输入缓冲器。

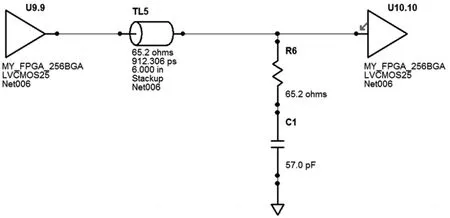
图17 阻容端接仿真示意

图18 不同C1下，RC端接信号波形

当并联电阻R6的阻抗一定时，随着C1容值的增加，过冲越来越小，同时，信号的上升速度逐渐变缓。阻容端接并不会影响信号线上的高电平电压，当信号刚到达阻容端接时，电容C1以时间常数RC进行充电，有电流流过电阻R6，此时电阻R6起到并联端接的作用。随着时间的推移，电容C1两端的电压逐渐稳定，此时不再有电流流过电阻R6，且接收端的电压等于输出端的电压。

3.6 二极管端接

二极管端接，即在信号输入端口位置并联一个上拉到Vpullup的肖特基二极管SBD1和一个下拉到地的肖特基二极管SBD2，如图19所示。该端接方法利用了肖特基二极管的快速导通特性以及限幅原理，通常要求二极管的开关速度至少要比信号上升时间快4倍。由于这种端接方案在实际应用中并不常用，所以在此不再赘述。

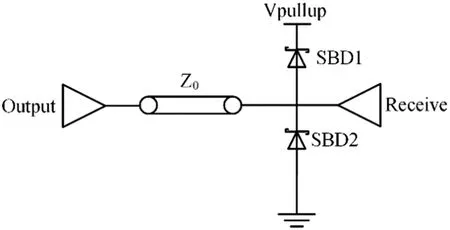
图19 二极管端接示意

4 结束语

随着汽车控制器上信号速率的提升，如何保证高速电路的信号完整性是每一个汽车电子工程师都需要考虑的问题，而保证信号完整性的一个核心要点就是如何抑制反射。通过仿真软件Hyperlynx对6种常用的端接方法进行仿真验证，仿真结果表明，上述的几种端接方法都可以有效地抑制信号的反射。在实际应用中，工程师可以通过选择合适的端接方法来抑制反射，从而提高产品的可靠性和竞争力。