适用于计算机程序计算的湿空气计算方法

王童 高丽颖

中国建筑科学研究院有限公司

在供暖通风、空气调节等领域经常会涉及到湿空气计算问题。传统方法是通过查找焓湿图进行分析的。然而，这种方式往往不太方便而且难以保证精度。目前市场上存在一些商业软件可以进行湿空气计算，但是这些软件通常不会公布其中的算法。因此，很难在需要开发新程序的时候提供参考。本文旨在给出一种适用于计算机程序计算的湿空气计算方法，以供需要编写涉及到湿空气计算的程序的读者作为参考。

1 饱和水蒸气压力的计算

湿空气计算中，较为困难的一个问题是如何计算空气的饱和水蒸气分压力。困难主要来源于饱和水蒸气分压力没有现成的解析公式，饱和水蒸气压力通常是将实测数据以表格形式给出。工程上已有一些饱和水蒸气压力经验计算公式，但是这些公式形式上往往都比较复杂。建立在这些经验公式上的湿空气计算方法也会比较复杂。

本文通过采用最小二乘法，对饱和水蒸气压力试验数据进行分段多项式拟合，从而得到一个饱和水蒸气分段计算函数。参考文献[1]附录1-1 中的表格列出了饱和水蒸气压力的实验数据。在-20～50 ℃范围内，表格从-20 ℃起，每隔 1 ℃给出一个对应于此温度的饱和水蒸气压力试验值。通过实验对比发现，对表格中每连续十个实验数据进行二次多项式拟合，得到的分段函数形式较为简单且精度较高。即先对-20 ℃至-11 ℃范围内的饱和水蒸气压力进行二次多项式拟合，得到拟合系数a1，b1，c1，之后对-10 ℃至-1 ℃范围内的饱和水蒸气压力进行拟合，得到拟合系数a2，b2，c2。以此类推，最后对40 ℃至-49 ℃范围内的饱和水蒸气压力进行拟合，得到拟合系数a7，b7，c7。

通过以上方式进行拟合可以得到一个如下形式的分段计算函数：

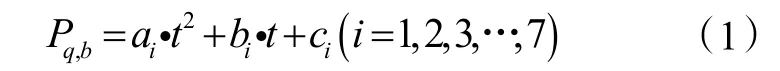
式中：Pq,b为饱和水蒸气压力值，Pa；ai，b i，c i为第i段饱和水蒸气压力函数的拟合系数；t为水蒸气温度，℃；

在所有常用的饱和水蒸气压力经验计算公式中，戈夫-格雷奇（Goff-Gratch）公式与实验的数据最为接近[2]。因此，本文将式（1）与戈夫-格雷奇公式进行对比。经过对比发现，式（1）与戈夫-格雷奇公式最大绝对误差小于35 Pa，平均绝对误差为7.2087 Pa。温度在-15 ℃至49 ℃范围内相对误差小于0.6%，-20 ℃至-16℃范围内相对误差小于2.5%。-20 ℃至49 ℃范围内平均相对误差小于0.35%。由此可见式（1）计算精度可以满足工程计算要求。目前主流的计算机编程语言均支持条件判断语句，可以用于表达式（1）这种形式的分段函数。因此，可以编写计算机程序对式（1）进行求解。

由于式（1）所表示的分段函数在-20 ℃至50 ℃是单调递增的，因此在此区间内存在反函数。将式（1）进行变换，可变为如下形式：

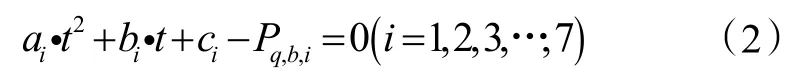
可以通过一元二次方程求根公式对式（2）进行变换（通过计算可以确定式（2）中每段函数在其定义域内判别式Δ均大于0。）。由此可得如下公式：

2 湿空气状态参数计算

工程中常用的湿空气状态参数有干球温度tw、焓值h、含湿量d、相对湿度φ、水蒸气分压力p q、湿球温度tw、露点温度tl。在这些状态参数中，有一些参数之间是相关的，例如：含湿量d与水蒸气分压力p q之间、焓值h与湿球温度tw之间、含湿量d与露点温度tl之间，都一一对应，知道其中一个参数就可以确定另外一个参数。根据湿空气原理可知，由任意两个相互独立的状态参数可以确定其余状态参数。后文会针对各种情况分别说明相应的求解方法。求解过程中除式（1）和式（3）外，还会用到如下两个公式：

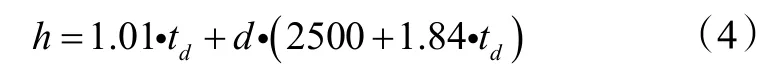
式中：h为焓值，kJ/kg；d为含湿量，g/kg；td为干球温度，℃。

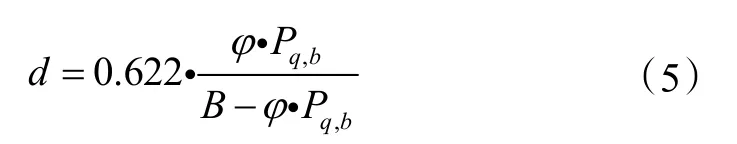
式中：φ为相对湿度；B为大气压力，Pa；P q,b为饱和水蒸气压力，Pa。

2.1 已知焓值h 及相对湿度φ 求解其余状态参数

当已知湿空气焓值h及相对湿度φ时，将式（5）代入式（4）消去含湿量d，然后再将式（1）代入新式中，消去饱和水蒸气压力P q,b。由此，可得如下形式的一元三次方程：

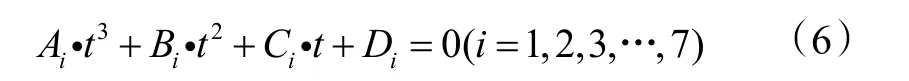
式中：Ai，Bi，Ci，Di为通过式（1）中第i段函数求得的一元三次方程的系数。

求解式（6）可以采用数值方法（例如牛顿迭代法）或者解析方法（例如卡丹公式法）进行求解。在求解式（6）时，由于干球温度td未知，因此需要进行试算。首先求解式（6）中第 1 个一元三次方程，可得干球温度值td,1。如果计算值td,1恰在-20 ℃至-11 ℃之间，则停止计算，此时td,1即为计算温度。反之，则继续求解式（6）中的第 2 个一元三次方程，由此可得湿球温度计算值td,2。如果计算值t d,2恰在-10 ℃至-1 ℃之间，则停止求解，此时td,2即为计算温度。反之，则继续求解式（6）中的第3 个一元三次方程。以此类推，直到求得的干球温度值td,i恰在第i个方程对应的温度范围内为止。如果，计算了式（6）所有方程式仍未求得计算温度，则可确定计算温度必不在-20 ℃至50 ℃之间。此方法求解干球温度值td最多需要试算七次。

将干球温度值t d代入式（1）可求得饱和水蒸气分压力Pq,b。将饱和水蒸气分压力值Pq,b及相对湿度值φ代入式（5）可求得含湿量值d。

2.2 已知焓值h 及含湿量值d 求解其余状态参数

将焓值h及含湿量值d代入式（4）可求解干球温度值t d。将干球温度值t d代入式（1）可得饱和水蒸气分压力值Pq,b。将饱和水蒸气分压力值Pq,b及含湿量值d代入式（5）可得相对湿度值φ。

2.3 已知焓值h 及干球温度值t d求解其余状态参数

将焓值h及干球温度值td代入式（4）可得含湿量值d。将干球温度值t d代入式（1）可得饱和水蒸气分压力值P q,b。将饱和水蒸气分压力值P q,b及含湿量值d代入式（5）可得相对湿度值φ。

2.4 已知含湿量值 d 及相对湿度值 φ 求解其余状态参数

将含湿量d及相对湿度值φ代入式（5）可得饱和水蒸气分压力值P q,b。将饱和水蒸气分压力值P q,b代入式（3）可得干球温度值t d。将含湿量值d及干球温度值td代入式（4）可得焓值h。

2.5 已知含湿量值 d 及干球温度值 td求解其余状态参数

将含湿量值d及干球温度值td代入式（4）可得焓值h。将干球温度值t d代入式（1）可得饱和水蒸气分压力值P q,b。将饱和水蒸气分压力值P q,b及含湿量值d代入式（5）可得相对湿度值φ。

2.6 已知干球温度 t d及相对湿度值 φ 求解其余状态参数

将干球温度t d代入式（1）中，求得饱和水蒸气分压力值P q,b。再将饱和水蒸气分压力值P q,b及相对湿度值φ代入式（5）可求得含湿量d。最后，将干球温度t d及含湿量d代入式（4）可求得焓值h。

2.7 湿球温度t w与焓值h 相互求解

焓值为h的湿空气湿球温度tw与焓值为h且相对湿度等于100%的湿空气干球温度相等。因此，在已知焓值h的情况下，可采用 2.1 节所述方法求解湿球温度t w。

反之，湿球温度为 tw 的湿空气焓值与干球温度等于t w且相对湿度等于100%的湿空气焓值相等。因此，已知湿球温度t w情况下，可以采用 2.6 节所述方法求解焓值h。

2.8 露点温度t l与含湿量d 的相互求解

含湿量为d的湿空气露点温度tl与含湿量为d且相对湿度等于100%的湿空气干球温度相等。因此，已知湿空气含湿量d情况下，可以采用 2.4 节所述方法求解露点温度t l。

反之，露点温度为tl的湿空气含湿量d与干球温度等于t l且相对湿度等于100%的湿空气含湿量相等。因此，已知湿空气露点温度tl情况下，可以采用2.6 节所述方法求解含湿量d。

2.9 水蒸气分压力与含湿量d 的相互求解

湿空气水蒸气分压力与含湿量存在一一对应关系。可通过下式对它们进行求解：

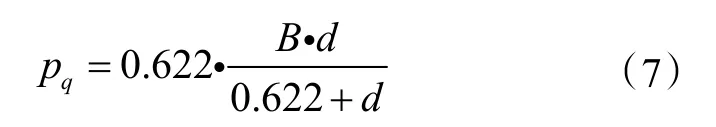
式中：P q为水蒸气分压力，Pa；B为大气压力值，Pa。

3 计算数据与实验数据的对比分析

为了分析本文所述计算方法的计算精度，笔者将计算数据与参考文献[1]附录1-1 中的实验数据进行了对比。为了更为全面的分析计算结果，笔者分别对四种情况进行了分析。这四种情况分别是：1）采用干球温度实验数据计算其余状态参数。2）采用含湿量实验数据计算其余状态参数。3）采用饱和水蒸气分压力实验数据计算其余状态参数。4）采用焓值实验数据计算其余状态参数。对比分析结果详见表1 至表4 中数据所示。

表1 计算数据与实验数据的最大绝对误差统计

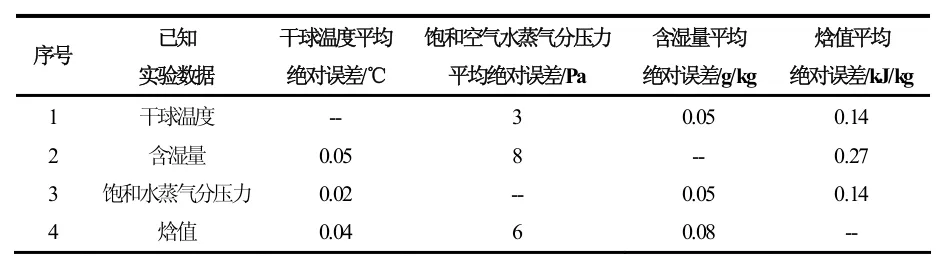
表2 计算数据与实验数据的平均绝对误差统计

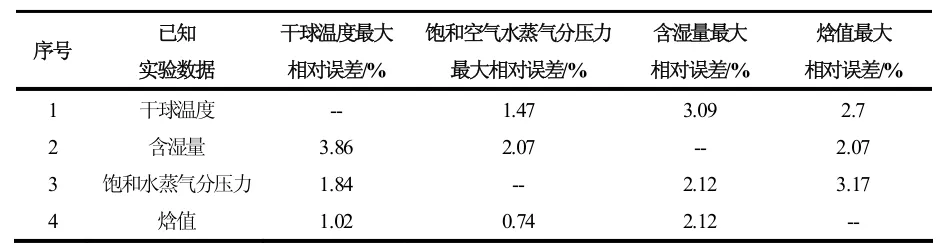
表3 计算数据与实验数据的最大相对误差统计

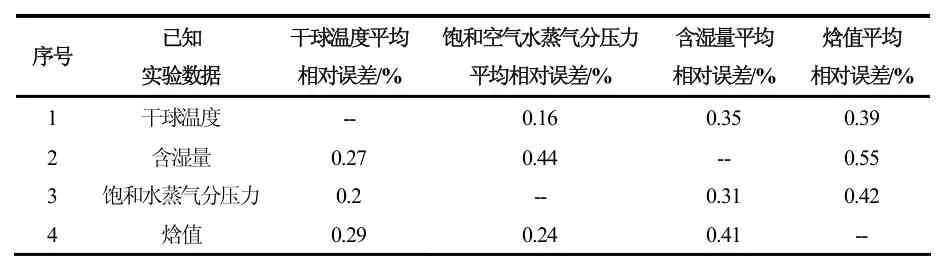
表4 计算数据与实验数据的平均相对误差统计

4 结论

本文提出一种适用于计算机程序计算的湿空气状态参数计算方法。文中介绍了各种情况下的湿空气计算方法。并且，将计算结果与实验数据进行了对比分析。分析结果显示，本文所述方法具有较高的计算精度。

此外，笔者曾经利用本文所述方法编写过基于湿空气计算的空调机组选型软件。实践证明，本文所述方法适用于编写需要进行湿空气状态参数计算的计算机程序，并且计算精度满足实际工程需求。