基于材料热阻的辐射空调末端换热性能分析
韩成
东南大学能源与环境学院
0 引言
对于毛细管换热器来说,其末端热工性能一直都是研究的重点:表面温度和表面换热量。从现有的研究来看,主要一是从辐射板的结构因素、施工因素、运行因素等方面研究。如高志宏等人通过比较不同位置的辐射板,发现热源温度低时对流换热量较大,热源温度高时辐射换热量较大[1]。二是对辐射板实验测试标准的研究,如杨瑞等人通过比较不同国家的标准,提出了将标准中的内热源法与外热源法相结合的测试方法[2]。但现有的研究中缺乏对辐射板末端热工性能直观、简便、具有共性的评价方法,辐射板的热工性能会随着换热温差,室内环境及冷热模式的变化有所差异。同时没有考虑实际工程中一些安装工艺的影响,毛细管换热器表面覆盖的装饰涂料[3],如半水石膏、水泥砂浆、抹灰等,导热系数从 0.2 W/(m·K)到 1.7 W/(m·K)不等。由于材料热工性能的差异对辐射板的换热性能影响较为明显,因而现有的评价方法并不能反映不同安装工艺的辐射顶板的热工性能。
本文根据等效电阻理论,在地埋管换热阻容模型[4],阻容 RC 模型[5-6],等效热阻模型[7-8]的基础上提出材料热阻的概念,建立了一种评价辐射顶板热工性能的算法,其简便,直观,精度高的特点对于工程应用具有实际参考价值。
1 毛细管辐射空调末端材料热阻理论模型
材料热阻是指简化辐射板内传热过程中热阻的总和,从整体上描述辐射顶板表面的换热性能影响,具有直观性和简便性。为了简化顶板辐射板的模型,做出如下假设[7]:
1)认为保温层是一个绝热表面,同时将三维传热看作为二维传热,即热量只向室内方向传递。
2)毛细管换热器内的介质流动为均匀流,各层材料各向同性。
3)认为室内温度分布均匀。
本文以贴附式毛细管换热器为例,顶板敷设面图如图1 所示[8]:

图1 贴附式毛细管换热器
供冷(热)顶板表面和室内环境进行辐射换热和对流换热,即除材料热阻外,还存在辐射换热热阻和对流换热热阻,两者之和记为综合换热热阻。毛细管辐射换热热阻模型如图2 所示[11]:
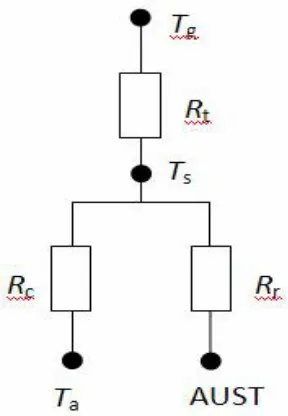
图2 顶板辐射热阻模型
图2 中:Tg是供水温度,K;Rt是材料热阻,(m2·K)/W;Ts是辐射顶板室内侧表面平均温度,K;Rc为辐射顶板表面自然对流换热热阻,(m2·K)/W;Rr为辐射顶板表面辐射换热热阻,(m2·K)/W;Ta为室内空气的平均温度;AUST 则为室内非供冷(热)表面的平均辐射温度,K。稳态传热时,材料热阻可由下式计算:

式中:q为辐射顶板表面与室内换热量,W/m2;Gw为毛细管内水流量,kg/s;cw为水的比热容J/(kg·K);Tg和Th分别为供回水温度,K;A为辐射顶板换热面积,m2。
2 辐射顶板的模拟分析
2.1 物理模型
本文以贴附式 S 型毛细管换热器[1]为研究对象,先将毛细管网珊固定在保温层表面,再在毛细管网珊表面覆盖一定厚度的装饰层,图 3 是用GAMBIT 软件建立的毛细管换热器模型,重力方向为-y 轴:

图3 辐射顶板模型
2.2 边界条件的设定
1)定量条件:毛细管的材质为 ppr 塑料,导热系数为 0.26 W/(m2·K),管径为 4 mm,管间距为 10 mm,单根管长为 1 m,壁厚为 0.5 mm,毛细管内流动的介质为水,供水流速为 0.1 m/s。装饰层的材料的厚度为10 mm。经计算,供冷工况下辐射板室内侧表面综合换热系数取9.5 W/(m2·K)。供热工况下辐射板室内侧表面综合换热系数取6.2 W/(m·2K)[12]。
2)变量条件:室内为稳态换热,在供冷时室内设计温度ta分别设置为24 ℃,25 ℃,26 ℃,27 ℃,每组室内设计温度下分别设置 16 ℃,17 ℃,18 ℃的供水温度tg,按顺序分别记作W1~W9。在供热时室内设计温度ta分别设置为 16 ℃,18 ℃,20 ℃,22 ℃,每组室内设计温度下分别设置 35 ℃,36 ℃,37 ℃的供水温度tg,按顺序分别记作W1’~W12’。装饰层材料的导热系数λ分别设置为0.1 W/(m·K),0.3 W/(m·K),0.5 W/(m·K),0.7 W/(m·K),0.9 W/(m·K)共5 组。
2.3 材料热阻的模拟结果分析
图4 和图5 分别展示了在模拟制冷工况和制热工况时材料热阻的变化规律。由图可知,在不同的供水温度和不同的室内设计温度时,同一种辐射顶板装饰层材料的材料热阻基本上是一个定值,材料的导热系数越大(在 0.5 W/(m·K)及以上),材料热阻值就越稳定。而不同种材料的辐射顶板装饰层的材料热阻值相差较大。并且同种装饰层材料在冷热两种工况下材料热阻值基本相同。该模拟结果符合本文使用材料热阻来预估辐射顶板表面换热性能的想法。

图4 供冷时辐射顶板的材料热阻
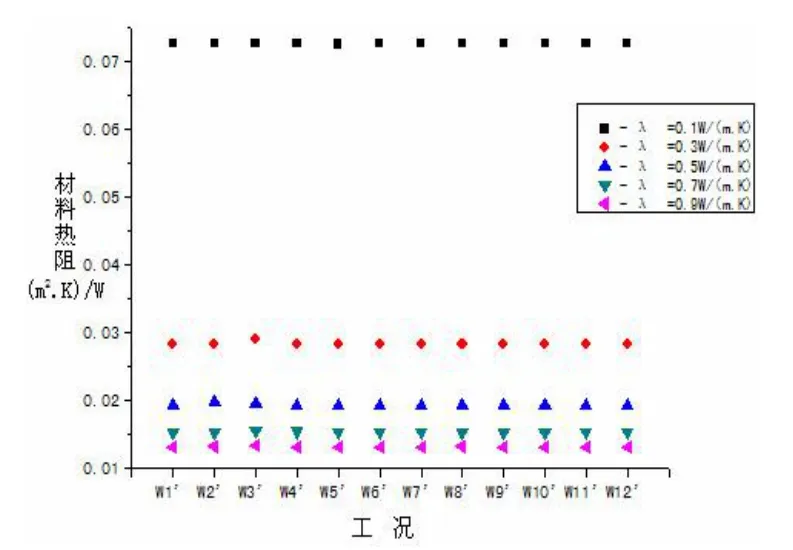
图5 供热时辐射顶板的材料热阻
辐射顶板装饰层导热系数的大小对其材料热阻的影响较大,表 1 给出了供冷辐射顶板材料热阻的工程模拟值,由于样本容量小,因此所得结果不具备广泛应用的基础。

表1 辐射顶板的材料热阻分析
为了进一步研究不同材料装饰层的材料热阻,本文根据表1 的数据对导热系数和材料热阻的函数曲线图进行拟合,拟合的结果如下式所示:
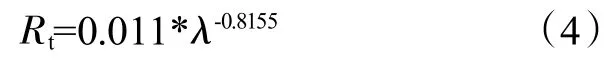
经Origin 软件的数据拟合,得到材料热阻Rt和装饰层材料导热系数λ的无量纲函数,拟合度 Adj.R-Square 为0.99837。
为了进一步验证拟合函数的准确性,本文在原有模型的基础上,选取装饰层导热系数λ=0.2 W/(m·K)时,对工况W1~W12 进行模拟。表 2 展示了分别采用拟合函数预估和软件模拟两种方法得到的材料热阻值,模拟结果表明,采用该拟合函数预估得到的材料热阻值与模拟得到的材料热阻值误差在5%以内,用来描述材料热阻和导热系数的变化规律基本准确。

表2 材料热阻偏差
3 材料热阻的工程应用
基于材料热阻Rt和辐射顶板热阻模型,可以按照以下步骤进行工程预估:
1)确定设计参数:供回水温度,装饰层材料的类别,室内设计温湿度,辐射顶板的面积及冷热工况。
2)根据冷热工况选择相应的拟合函数预估辐射顶板的材料热阻值。
3)根据式(3)代入材料热阻表达式及综合换热系数,按下式计算辐射顶板表面平均温度,表面平均热流密度,水流量,对辐射顶板换热性能进行工程评价。
供冷:
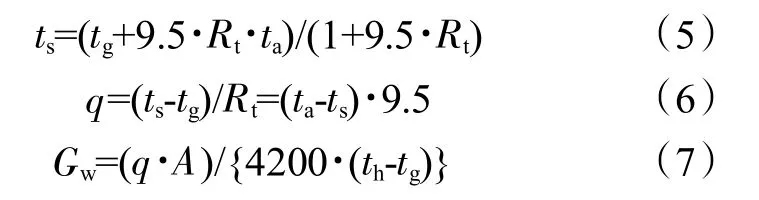
供热:
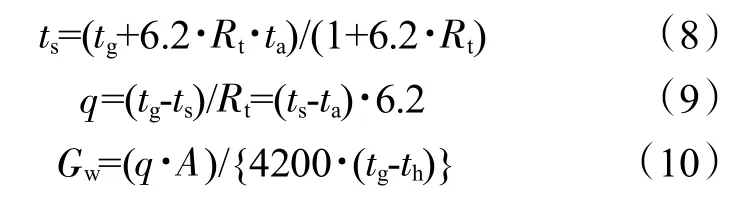
式中:ts为辐射顶板表面平均温度,℃;Rt为材料热阻,(m2·K)/W;ta为室内温度,℃;q为辐射顶板表面平均热流密度,W/m2;A为辐射顶板面积,m2;tg和th分别为供回水温度,℃。
以某工程为例,输入参数为表3 中的值时,表 4 即为得到的工程预估值。

表3 输入工程参数

表4 输出的工程预估值分析
4 结论
本文提出材料热阻的概念,从整体上描述装饰层材料导热性能的差异对辐射顶板换热性能的影响,并拟合了辐射顶板的材料热阻和装饰层材料导热系数的函数表达式,从理论模型、模拟验证、案例分析的角度论证了材料热阻的可行性。结果表明,基于材料热阻模型的工程预估应用范围广、实用价值大、工程精度高。

