“图解数学”助力课堂生长

陈云

“图解数学”指的是运用图形、表格、公式等可视的方式把学生本来不可视的思维（思考方法和思考路径）呈现出来，使其清晰可见，它是“思维可视化”在小学数学课堂中的主要运用方式。“图解数学”不要求用专业的“可视化”工具，也不像“思维导图”那样要求图文并茂地把各级主题的关系用相互隶属与相关的层级图规范地表现出来。相反，我们只是尊重儿童生来喜欢涂鸦的天性，尊重儿童喜欢并善于用画图表达自己感觉、感受的特点，引导学生用自己喜欢的方式去展开数学的表达。“图解数学”的方式更加符合小学生的年龄特点和理解水平，带有比较多的随意性和随机性，更具个性特色，能让不同层次的学生都能带着自己的理解参与到交流、互动中，为学生提供直观形象的理解工具，也为创新意识的培养提供更多的可能。

一、“图解数学”助力学困生搭建通向理解的阶梯

我们从不愿意给学生分出三六九等，但不可否认，在任何一个班级里，学生都会存在差异，这种差异的形成原因是多方面的，而且比较难以改变。所以，我们的课堂教学总是会面临这样的两难境地：一个知识学习结束，一部分学生已经心领神会，可以做到触类旁通、轻松应对，却还有一部分学生依然懵懵懂懂，做题时无从下手。即便后期有老师、家长提供“小灶”支持，这部分学生也不过是“照葫芦画瓢”、熟能生巧罢了。虽然“学困生”的产生原因是多元的，但有些数学知识本身的抽象、严谨、碎片化、难以理解等也一定是困住学生的原因之一。针对这样的情况，教师运用好“图解数学”就可以帮助学生突破“理解”这道坎，丰厚学生的感性认知，缓解学生的焦虑感和无力感。

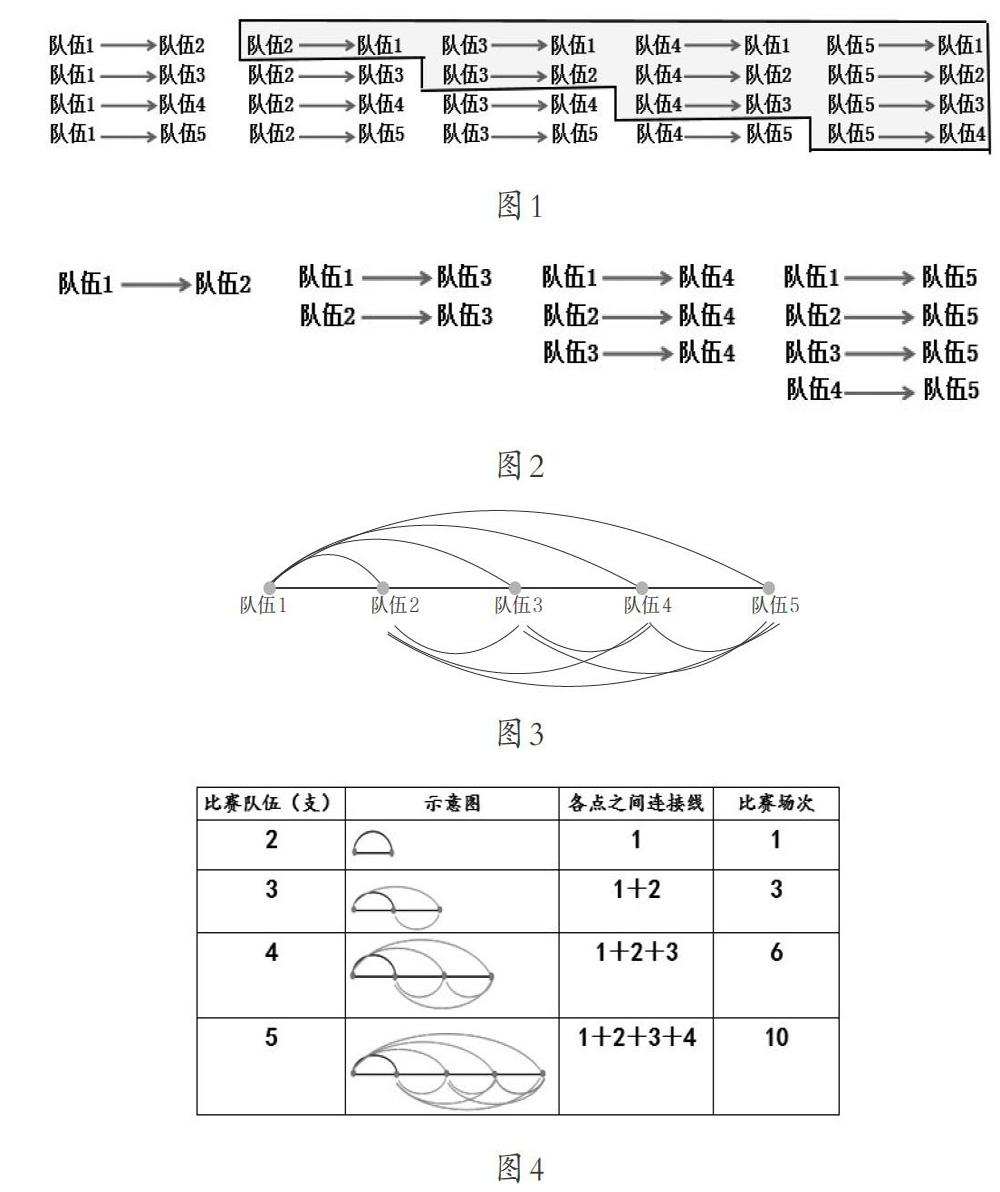
如“比赛场次”问题的学习：“5支队伍参加，每两支队伍之间要进行一场比赛，一共要进行几场比赛？”有的学生可以很快想到4+3+2+1=10（场），但总有学生怎么都弄不明白这个算式背后的道理，我们尝试让学生用自己所能理解的方式记录比赛场次，有的学生从最原始的匹配状态进行“图解”，排列出每一场赛事，剔除其中重复计算的赛事（图1），这样就能比较直观地解释算式的由来了。但很显然，最原始的排列图不足以让学生感悟这一类问题的研究方法，我们继续引导学生把队伍逐渐增加的过程“图解”出来（图2），这样的解释更容易发现每增加一支队伍会增加几场比赛，以及为什么会增加这些场次，从而进一步感知比赛场次中的规律。在此基础上再启发学生把一一列举逐步抽象成点和线的表达方式（图3），数学抽象和模型意识就在不经意间得到提升。最终再用数字、图示和算式的相互结合来梳理其中的数量结构（图4）。至此，学生就可以很直观、很轻松、很透彻地理解这一类问题的解决方法和解答原理了，“学”因此不再被“困”。

如上所述，图形是一种奇妙的数学语言，可以从最简单、最直观的排列开始，一步一步地帮助学困生体会和理解数量关系的产生原因、发展过程和变化规律，让抽象的、碎片化的、难以理解的数学知识显性化、可视化。

二、“图解数学”助力中等生发现突破瓶颈的钥匙

小学数学知识基础性较强，解决一道题的难度往往不会太大，但基于小学生的理解能力和智力发展的情况，想要达到举一反三、触类旁通，恐怕也是我们教学中难以突破的瓶颈。这样的瓶颈若能突破，则曲径通幽，收获的不仅是知识，更是能力、是数学的思想方法;倘若不能突破这个瓶颈，就会对知识一知半解。而不少教师在教学设计时也容易受限于“这个内容我怎么教”的惯性思考，较少关注“这个内容学生是怎么学的”，这就导致就题论题的现象比较突出，不利于学生养成从不同的问题情境中找出同一结构关系的数量关系模型的思维习惯。解决这一问题，我们不妨让学生先学，然后把自己学的过程“图解”出来，或许这些“图解”会成为解决一类问题的模式，或许学生能在“画图”“析图”的过程中自己“破茧”，也或者教师们能从中得到些许提示，助力学生突破瓶颈。

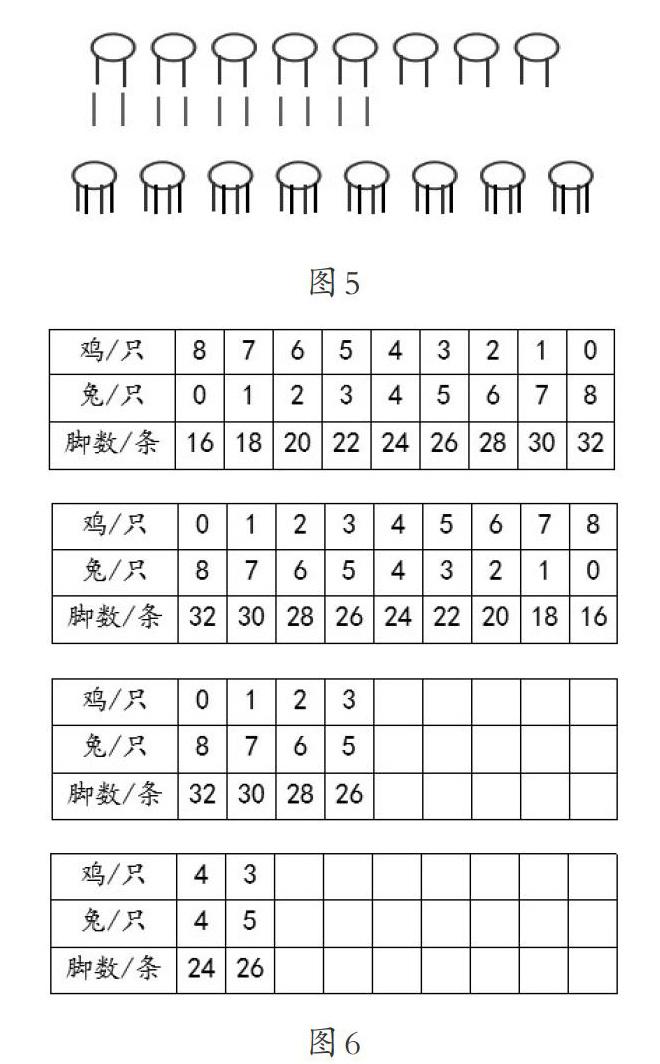
如“鸡兔同笼”问题的学习：“鸡兔同笼，头有8个，脚26条，问鸡、兔各有几只？”除了“推算”外，教师再让学生选择自己喜欢的方式“图解”出自己的思考过程，学生有了不同的表达（图5），不妨比较一下，这几种画法的不同点在哪里？有相同的地方吗？在对直观图示的解读中，学生发现：先假设都是鸡或都是兔，然后把多出的（或少的）数量分配掉。这就取得了与“推算法”原理上的联系，使推算过程中每一步都更有说服力。再来看列表枚举（图6），方式也很多，但我们的目标一定不是找到更多列表的方式，只是利用这些表格展开横向、纵向的比较：每一种列表方法的优势、劣势在哪里？为什么有的列表可以很简单？列表、画图、推算等不同方式，其本质的思想都是什么？这样的方法还可以用来解决哪些问题？很显然，“图”“表”“推算”的思路都是符合“假设—比较—调整”的过程。那么对于“8桌球赛，有26人参赛，单打、双打各有几桌球赛？”这样的问题我们就可以假设都是单打，再对不足的人数进行调整;对于“8枚硬币，共3元2角，5角、2角各几枚？”这样的问题我们就可以假设都是5角，再对多出的部分进行调整。可以看出，借助多重“图解”的比较，学生轻松掌握了分析解决这一类问题的工具，数学思维也得到发展。

如上所述，学生尝试把自己认为很乱、很复杂、很麻烦的各种情况进行梳理时，就已经慢慢学会透过形式走向实质了，原来种种变式都万变不离其宗，这个“宗”就是同一结构关系的数量关系模型。这样的“图解数学”能帮助中等学生更深层地领悟到数学的内在联系，追溯本节课“知识目标之上的目标”。

三、“图解数学”助力优等生打开创新意识的大门

在今天这样一个复杂而多变的世界，努力培养学生的好奇心，启迪学生的创新意识显得尤为重要。如何培养学生的创新意识呢？首先要让学生投入积极探索、主动思考的状态中去，只有学会了独立思考才有可能创新。但是需要注意的是，独立思考不等同于一个人孤立地冥思苦想，学生独立思考之后还应该经历与他人合作交流解决问题的过程，从不同的思考路径和思考成果中归纳概括，得到猜想，并加以验证，这才是创新的重要方法。那么，独立思考的成果如何表达？合作交流中如何分享？概括归纳时如何改进？……要解决这些问题，那就要引导学生写出来、画出来，以“图”记录思路，借“图”表达想法，凭“图”交流碰撞，用“图”展示成果，让学生的独立思考、合作交流、歸纳概括有底气、有工具、有抓手。

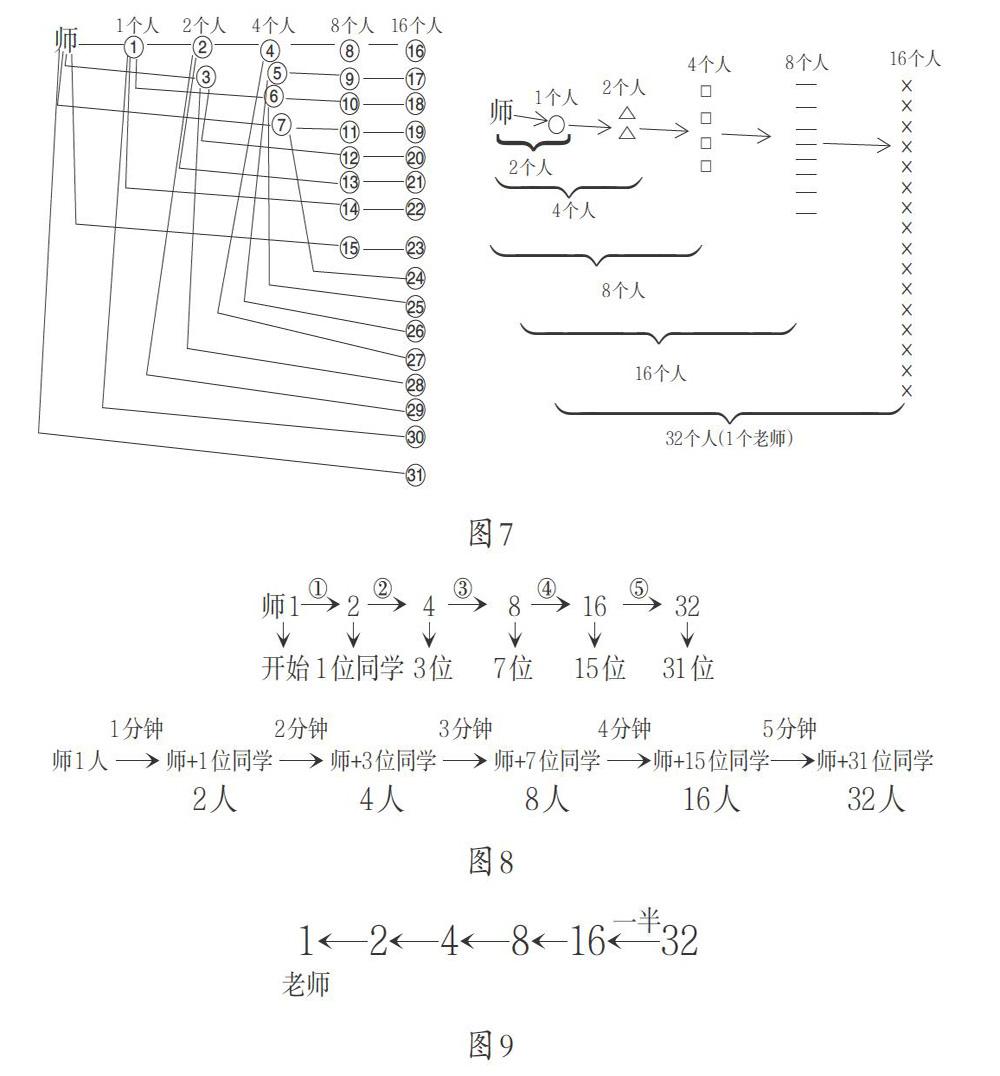
如“倍增问题”的学习时有这样一个问题：“老师有一个重要的消息需要在最短的时间通知到全班31个同学，每通知一个同学需要1分钟，已经接到消息的同学可以帮忙通知下一个同学，最少多长时间可以让全部同学得知消息？”在教师对学生最初始的做法进行梳理后，学生开始独自修改方案，运用到有序思考的策略，小组内同学将最优化和最有序的作品推荐出来（图7），小组作业的集中展示，有些同学理解了“倍增”的过程，也有同学并不满足于发现了“倍增”的规律，尝试用更简易的线性图（图8）概括人数的发展变化。线性的结构更容易突出主干上倍增的数据，这种方便、容易上手的可视模型出现后，一部分学生迅速内化知识，并开始“浮想联翩”：有同学想到了加上老师其实就是32个人，可以从32人入手，倒推出时间（图9）……最后，教师给学生一张只涂了一格的密密麻麻的方格图，按照“倍增”的方法动手圈一圈看看几次能涂满。直观图示带来的震撼，再配合“在棋盘中放米”和“荷叶多长时间长满池塘”这样有趣的“倍增”问题，有助于培养学生的数学核心素养。

如上所述，学生利用知识结构图构建起思考路径的网络，既能使已有知识条理化、系统化，又能对未来的知识有合理猜想，这样的学习过程中学生不仅眼中有数学知识，心中还有数学思想。这样带着创新思考的数学学习才会改变学生单向接收知识的学习状态，变为自主体验知识、乐于展示知识、敢于创新知识的学习状态，是真正有价值、有远见的学习。

“让不同的人在数学上得到不同的发展”，这是我们的课堂得以良性生长必须达到的目标，“图解数学”恰好可以引导学生真实参与数学知识的发现和创造过程，使得不同需求的学生都能在数学学习中获得智慧的启蒙，这种生长的力量能赋予课堂更多的魅力。

（作者单位：南京师范大学苏州实验学校）

责任编辑 周瑜芽

E-mail：405956706@qq.com