考虑余-废料资源回收的车间物料配送路径规划研究

张守京，张 仪

(西安工程大学1.机电工程学院；2.西安市现代智能纺织装备重点实验室,陕西 西安710048)

激烈的全球化竞争以及市场环境的不可预测性迫使离散制造企业的生产模式向多品种、小批量转变。该生产模式的产品结构较为复杂，产品物料种类繁多。一方面，物料能否准确、及时、高效地送达工位直接影响到生产能否正常进行；另一方面，因订单变化、加工异常所产生的剩余物料以及残次品等余-废料资源处理不及时、占用生产空间，也在一定程度上影响了企业生产的顺利进行。车间工位物料配送、余-废料资源回收处理均需对运输小车进行调度以及运输路径规划(vehicle routing problem，VRP)。工位物料配送和余-废料资源回收协同优化问题在一定程度上与装卸一体化车辆路径问题

(vehicle routing problem with simultaneous pickup and delivery，VRPSPD)类似，均需考虑配送和回收需求，即运输小车将物料配送至工位同时将余-废料从工位处回收，并满足工位处物料先卸载后装载的顺序。这能够有效减少物流资源浪费，提高车间运输小车利用率、降低物流运输成本[1]。

目前，众多研究学者对离散制造车间物料配送VRP问题以及逆向物流中VRPSPD相关问题进行了深入的研究。在物料配送的VRP问题上，文献[2]针对车间作业环境的不确定性，提出了计及漂移瓶颈的时变物料配送路径优化方法，在动态物料配送路径的优化问题上给出了新的解决思路。文献[3]对多自动导引车物料配送路径规划问题进行分析，并将自动导引车使用数目、行驶费用和时间窗偏离费用作为优化目标建立数学模型，求解物料配送路径规划问题。文献[4]以实时和多源制造数据为基础，设计了车间物料搬运的动态优化模型，实现了物料配送的动态优化。文献[5]考虑生产节拍波动引起的物料需求时间变化，建立了带模糊软时间窗的物料配送路径优化模型，并结合动态规划-模拟退火算法对模型进行求解。VRPSPD[6]最初由Min[7]在1989年提出，解决了在车辆数确定和车辆负载能力有限的条件下，1个中心图书馆与22个地方图书馆之间图书发送与回库的问题。文献[8]在节点需求小于等于车辆容量的VRPSPD基础上，引入节点访问次数限制，将节点需求与车辆容量关系扩展到允许节点需求大于车辆容量的情形。文献[9]采用遗传算法求解VRPSPD问题，并利用Augerat数据集进行验证，结果证明该方法具有较好的稳定性。文献[10]以最小化总成本、最小化车辆数目等为目标，采用联合进化遗传算法进行求解，取得了较好的求解效果。

本文在离散制造车间物料流循环现状和上述文献研究[11]基础上，分析得出离散制造车间生产过程中存在以下问题。1)工位物料配送不及时，满意度较低；2)车间内部分生产物流以单向流动为主，未形成有效物流闭循环，例如，物料配送或物料回收过程均存在空车行驶状态；3)工位余-废料资源处理不及时，资源循环利用率低并占用一定生产空间。针对以上问题，结合车间物料流循环与VRPSPD相关研究，本文提出了车间物料再循环策略。将物料配送和余-废料资源回收相结合，实现车间内物料流闭循环流动；并以物料流循环总成本为优化目标构建数学模型，最后借助遗传算法对该问题进行求解，通过实例对模型和算法的有效性、可行性进行了验证。

1离散制造车间生产环境分析

1.1 车间生产环境布局与物流分析

通过对离散制造车间内部环境分析[12-13]，构建其生产环境布局。如图1所示，左侧为3类存储中心，产品库包括半成品库和成品库；物料库包括原材料库、零部件库、设备维修备件库；余-废料资源库主要存储车间生产过程中产生的废料、边角料、残次品等。右侧有16个生产工位，每个工位均设有1个物料缓存区、1个产成品放置区[14]，工位四周为行驶路径。

图1车间生产环境布局Figure 1 Workshop production environment layout

物料流循环流程以原材料、零部件配送和余-废料、产成品回收为主[15]，其循环流程如图2所示。实际车间物料流循环中物料配送和余-废料、产成品回收过程均采用分阶段、单任务模式，即以物料配送、余-废料回收分别作为单个作业任务。该模式分工明确、简单易行，但同时易造成运输资源浪费、运输成本较高。本文针对车间生产物流循环过程整体研究，将物料配送与余-废料资源回收需求共存的工位作为研究对象，提出物料配送与余-废料资源回收协同优化的物料再循环策略以改变现有车间生产物流模式，实现车间内有效物流闭循环。

图2物料流循环Figure 2 Material flow cycle

1.2考虑余-废料资源回收的物料再循环策略

车间内余-废料资源处理步骤如图3所示。其中，工位余-废料资源回收方式[16]主要有2种方式。1)定期回收，按照车间余-废料资源回收计划，在一定的时间周期内进行回收，但是容易出现余-废料过多占用工位存储空间的状况；2)定量回收，根据工位余-废料资源存储箱容量设置相应警戒线，当存储箱内余-废料资源存储量达到警戒线时进行回收。定量回收和定期回收均易造成资源循环利用率低、运输成本高、占用较多生产空间等问题，影响正常生产。

图3余-废料资源处理Figure 3 Disposal of remaining material and abandoned material resources

生产过程中，因车间生产环境等不确定因素，需要对工位进行实时物料补充。同时，结合工位余-废料资源回收不确定性，将物料配送与余-废料资源回收协同考虑，构成物料配送与余-废料资源回收协同优化任务，该任务执行过程如图4所示。其中，红色线条表示小车行驶路径；黄色箭头表示物料卸载；蓝色箭头表示余-废料装载。任务规则如下。

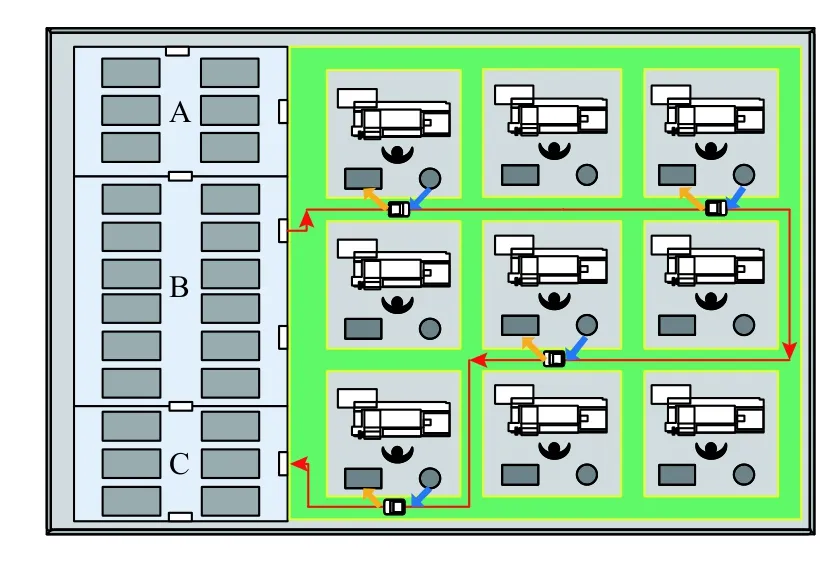
图4物料配送和余-废料资源回收路径规划Figure 4 Material distribution and recycling of remaining materials and abandoned material resources path planning

1)各工位处余-废料回收量不超过运输小车最大装载量。

2)任务执行过程中，工位物料卸载优先于余-废料资源装载。

3)工位需求物料不可拆分配送，余-废料资源可拆分回收。

2问题描述及数学模型

2.1问题描述

车间内含有装载量为Q的运输小车K台，共有N个工位需要物料配送，N*个工位余-废料资源待回收处理，各工位所需物料和待回收的余-废料资源数量、种类等均已知。物料再循环任务为运输小车将物料库中的物料配送至各工位处并将所配送工位的余-废料资源回收。运输小车最终将工位余-废料资源回收至余-废料资源库则任务完成。该任务需要满足以下约束条件。

1)车辆约束。运输小车启动、停止、碰撞、装卸时间等忽略不计，行驶速度恒定；所有小车同时从物料库出发，完成任务后返回仓库；每辆小车可以服务多个工位，每个工位只能由一辆小车服务。

2)工位约束。每个工位的物料需求量不超过运输小车的最大装载量，并且工位优先执行物料卸载，再执行余-废料装载。

3)时间窗约束[17]。如式(1)所示，物料在[RTi,LTi]内送达工位时，不存在惩罚；在RTi之前到达工位，惩罚因子为α，α=10；在LTi之后到达工位，惩罚因子为β，β=30。

2.2模型构建

模型参数如表1所示。

表1模型参数Table 1 Model parameters

根据以上论述，车间物料配送和余-废料资源回收协同优化模型表示为

上述模型中，目标函数为最小化车辆运输总成本，包括运输小车指派成本，运输小车行驶距离成本即物料配送距离成本与余-废料资源回收距离成本，需求工位时间窗惩罚成本。式中，i、j=0表示物料库或余-废料资源库；u=15，λ=1.5；式(2)为目标函数；式(4)表示工位i处去掉该工位物料需求量后的小车实际装载量大于该工位资源回收量时，小车回收量取该工位实际资源待回收量，否则，以该工位处小车剩余最大装载量回收余-废料资源；式(5)表示有K台运送车辆从物料库出发；式(6)表示每个工位只被服务1次且仅有1辆小车执行任务；式(7)表示满足工位物料需求量和车辆最大载荷量情况下，运输小车数量不超过车间内最大小车数量；式(8)表示每辆小车的装载容量不能超过小车最大载荷量。

3模型求解

本文主要研究车间物料配送和余-废料资源回收协同优化问题，即在满足物料配送时间窗要求前提下，采用物料再循环策略对车间工位需求物料进行配送，并对工位余-废料资源进行回收处理，从而优化运输小车行驶路径，并利用遗传算法进行求解，其运算流程如图5所示。

图5遗传算法流程Figure 5 Genetic algorithm flow

3.1染色体编码

在离散制造车间物料配送和余-废料资源回收、车辆分配、工位物料及余-废料方案选择基础上，采用三层自然数编码方式编码。例如，8个工位，3个物料库，1个余-废料资源库和3辆物料小车的运输方案矩阵M表示为

式中，x为工位编号，其中自然数表示物料配送的工位；*标记的自然数表示余-废料资源回收工位；y为物料库编号；z为车辆编号。工位4、7需要原材料，工位1、3、6需要零部件，工位2、5、8需要半成品部件，工位2、3、5、6、8含有待回收余-废料资源。车辆1负责工位1、5、8的物料配送并将工位1和工位8的余-废料资源进行回收，以此类推；M表示3辆车辆运输任务，车辆1为0-1-5-5*-8-8*-0，车辆2为0-3-3*-6-6*-7-0，车辆3为0-2-2*-4-0。

3.2适应度函数

适应度函数如式(9)所示，以个体i目标值C(i)倒数作为适应度函数，适应度值越大，则目标值越小。

3.3 种群初始化

种群规模为100，交叉概率Pc为0.95，变异概率Pm为0.08。初始种群的生成过程如下。

步骤1根据需求工位数量确定第1层染色体基因编号范围[1,N1]，根据车间存储库即物料库和余-废料资源库确定第2层染色体基因编号范围[1,N2]，根据工位物料需求量和车辆最大载荷量确定第3层染色体基因编号范围[1,N3]。

步骤2满足第1层基因数等于最大需求工位数并且工位基因编号无重复情况下，对每层染色体基因分别生成一个随机数ri∈[1，Ni]。

步骤3按照工位最佳配送时间，调整个体基因序列，将个体基因序列进行降序排列，每辆小车所能运输的所有工位代表一条物料配送路径。

步骤4重复执行上述步骤，直至达到初始种群规模。

3.4选择操作

选择操作采用精英保留策略和轮盘赌选择结合的方法。首先计算种群中染色体适应度值，将上一代种群中的所有个体按照适应度值升序排列，各个个体被选择的机率与自身适应度值成正比，选择适应度值最大的父代个体直接保留至下一代种群，并对剩余个体采用轮盘赌选择。

3.5交叉操作

交叉操作如图6所示。首先，随机选择染色体交叉区域；其次，识别已选择的染色体交叉区域，如果交叉区域中存在相同的工位基因值，则将其作为交叉操作的父代基因，否则，进行下一区域搜索，直到搜索到相同工位基因值，进行交叉操作。交叉后的染色体根据式(7)和式(8)判断是否为非可行解，是则重新执行交叉操作[18]。

图6染色体交叉Figure 6 Chromosomal crossover

3.6变异操作

随机数小于变异概率Pm，则进行变异操作，变异过程如图7所示。由于每个工位需要物料种类和数量及待回收余-废料资源是确定的，因此，在保持工位编号和物料库编号不变的情况下对车辆的编号进行随机变异，产生新的配送方案。同时，根据式(7)和式(8)检测变异后的染色体是否为非可行解，是则重新对染色体执行变异，直至产生有效染色体。

图7染色体变异Figure 7 Chromosomal mutation

4仿真实验与分析

某离散制造车间内设置有物料库、余-废料资源库以及16个生产工位。其中，各工位物料和余-废料资源清单如表2所示；物料配送中心到各工位以及各工位之间的的距离如表3所示；各工位时间窗如表4所示。由式(8)以及物料配送总量得出共需要3辆运输小车，小车最大载荷量是100 kg，行驶速度v=1 m/s，算例在Matlab r2014a上运算。

表2工位物料及余-废料清单1)Table 2 Workspace remaining material and abandoned material list

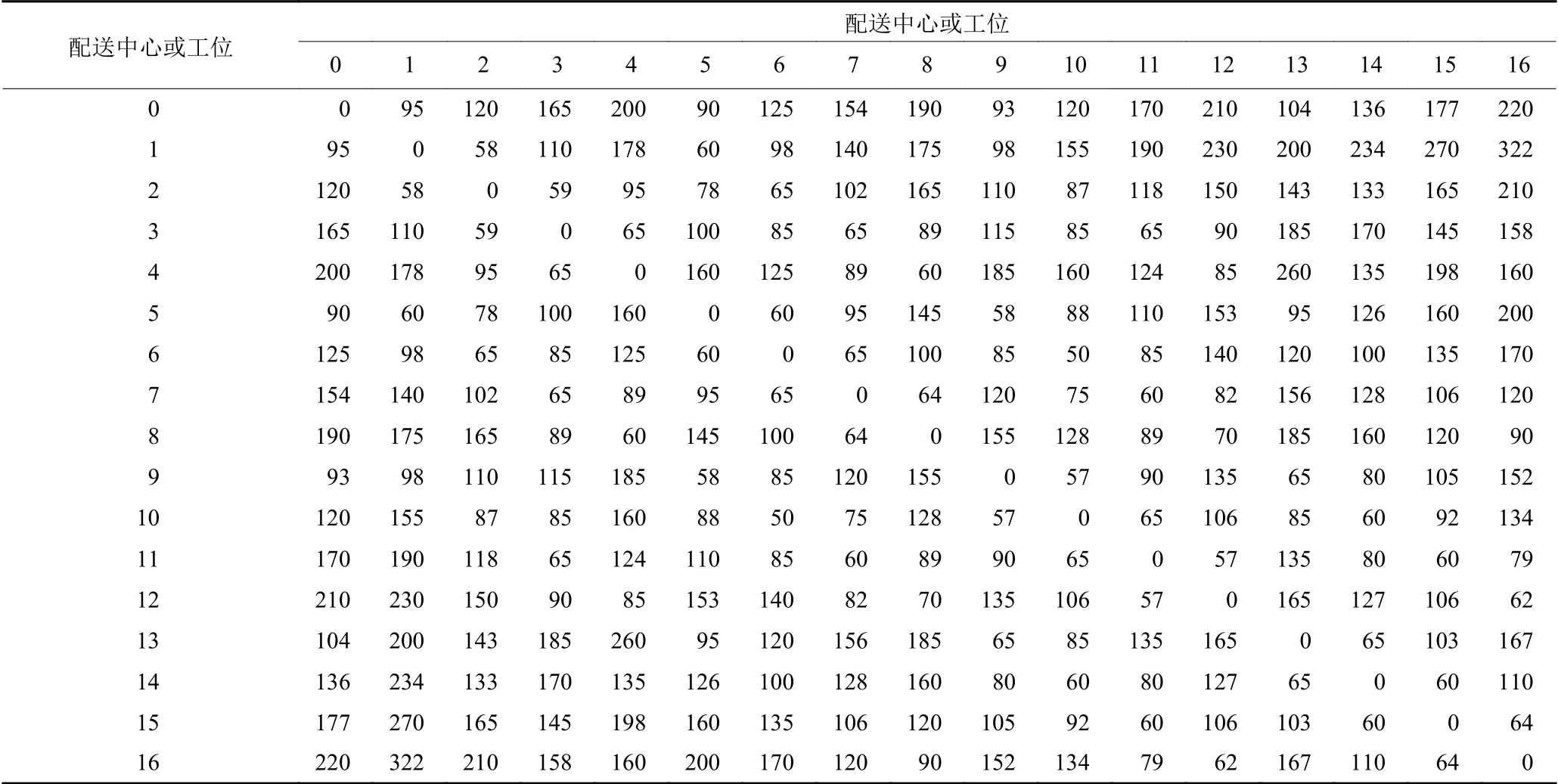
表3工位与配送中心间以及工位间的距离Table 3 Distance between station and distribution center and between station and station m

表4工位时间窗Table 4 Station time window

在进行仿真实验之前，对算法中包含的交叉、变异概率类型分析，遗传算法种群大小为100，迭代次数为100。在车间均为16工位的情况下，分别对算法中交叉概率(0.5～0.95)和变异概率(0.01～0.1)的取值范围进行分析，每种类型运算20次，结果如表5所示。根据表5分析得出，变异概率在0.06～0.1范围内能更快收敛得出最优值，交叉概率在0.75～0.95范围内算法运算比较充分，获得最优值迭代次数较小。因此，本文选取交叉概率Pc=0.95，变异概率Pm=0.08。

经过求解，算法在50次运行实验中，平均18代出现收敛现象，遗传算法迭代过程如图8所示；运输小车行驶路径如图9所示；物流总成本为 2 817.5，统计实验运行50次，最优结果如表6所示。①号小车配送路径为0-1-1*-2-2*-3-3*-15-15*-12-12*-16-16*-0；其中，车辆配送时装载率为99%和回收时装载率为89%；运输时间为12.40 min。②号小车运输路径为0-8-8*-13-13*-5-5*-9-9*-0；其中，车辆配送时装载率为88%和回收时装载率为81%；运输时间为10.35 min。③号小车配送路径为0-7-7*-10-10*-14-14*-11-11*-4-4*-6-6*-0；其中，车辆配送时装载率为91%和回收时装载率为84%；运输时间为11.50 min。

综上，本文采用车间物料再循环策略，在满足工位时间窗、工位物料需求的同时实现了车间余-废料资源及时、有效回收。车间物料配送和余-废料资源回收总运输成本为2 817.5 元；通过与未采用物料再循环策略车间物料配送与余-废料资源回收对比发现，总运输成本达到 5 279.8 元，降低了46.6%的运输成本，车辆利用率相比单一运输任务有所提高并实现了小车间均衡使用。

5结束语

本文以离散制造车间生产环境为研究对象，对车间物料流循环进行深入分析，提出了物料配送与余-废料资源回收协同优化的物料再循环策略，满足了车间物料准确、及时配送以及余-废料资源实时、有效回收。同时，降低了车间物料配送和余-废料资源回收成本，并实现了生产物流的闭循环。未来将在物料配送和余-废料回收过程中车间物流成本总体优化的基础上，对配送和回收的双时间窗优化分析，并在启发式算法上进行相应改进，实现生产车间内物料配送与回收双向动态优化。

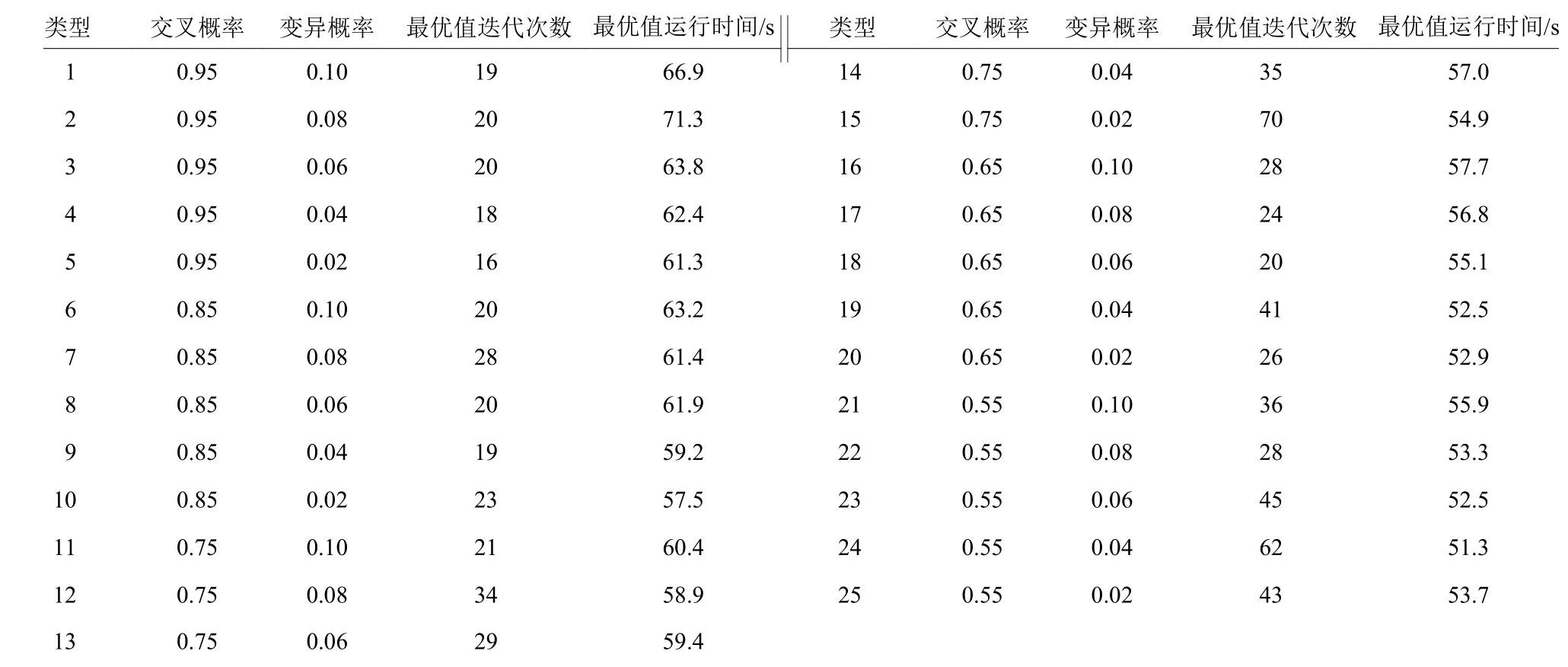
表5交叉、变异概率类型分析Table 5 Chromosomal crossover,mutation probability type analysis

图8算法迭代过程Figure 8 Algorithm iterative process

图9车辆行驶路径Figure 9 Vehicle driving path

表6 进化100代最优分配结果Table 6 Optimal distribution results after 100 generations of evolution