地震巨灾指数保险及其定价模型研究

管青青

一、 引言

巨灾是指发生频率较低，但损失金额十分巨大的自然灾害或人为灾难，如地震、台风、洪水和恐怖袭击等。 根据慕尼黑再保险公司的统计资料显示， 2018 年全球共发生850 起自然巨灾事件，灾害造成10400 人失去生命，直接经济损失总额高达1600 亿美元。 从1970 年到2017 年，按全球巨灾所致死亡人数统计的前十大事件中，地震自然灾害事件出现了6 次。 由此可以看出，一次偶然巨灾事件对社会、经济会带来许多无法估计的损失，地震巨灾保险的需求在不断增加，而相关保险产品的覆盖程度仍相对较低。

在国内，关于地震巨灾保险的研究主要集中在对我国地震保险的风险评估。 田玲和姚鹏(2013)以地震巨灾为例，研究了关于我国地震灾害损失分布函数。 郝军章和崔玉杰(2016)在POT 模型框架下，采用1961 ～2011 年中国发生的4.5 级以上地震样本，讨论了地震的巨灾风险度量与保险模式机制。 刘昕龙等(2017)研究地震巨灾保险共同体的风险转移效率，探讨了不同模式下巨灾风险转移效率及破产概率。 李云仙等(2017)提出用混合模型对地震巨灾风险进行评估，并讨论了混合模型的贝叶斯统计分析方法。

本文运用广义帕累托分布和广义可加等分布模型对巨灾指数保险进行相关研究，以我国新疆维吾尔自治区的地震损失数据为样本进行实证分析，运用R 软件对数据进行处理，建立地震损失数据分布模型，尝试根据地震震级设计合适的地震指数保险产品，并对地震巨灾指数产品进行定价，计算其纯保费。

二、 理论基础

(一) 广义帕累托分布

广义帕累托分布充分地利用样本数据的信息，主要用于研究超过某个阈值的样本损失数据所服从的分布。 其分布函数具体形式表示如下:

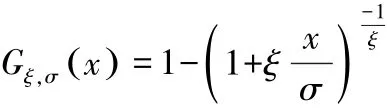
其中ξ是形状参数，σ是尺度参数。 当尺度参数不变，形状参数越大，广义帕累托分布的尾部越厚。 当形状参数ξ→0时，广义帕累托分布趋于指数分布，因此，广义帕累托分布也可以表示为:

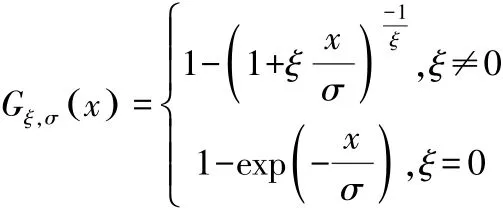
其中，当ξ＞0 时，x≥0；当ξ＜0 时，0≤x≤σ/ξ。

(二) 广义可加模型

广义可加模型在广义线性模型的基础上，在线性预测值中引入非参数函数，建立一般意义上的回归模型，广义线性模型仅是其中的一个特例。 广义可加模型由三个成分组成，分别为随机成分、系统成分和连接函数。

1. 随机成分

同广义线性模型，因变量的观测值yi是相互独立的随机变量，且服从指数分布族。 常用的指数分布族分布类型包括正态分布、泊松分布、二项分布、伽马分布、逆高斯分布和Tweedie 分布。

2. 系统成分

在广义线性模型系统成分的基础上添加了非参数函数部分，使得模型的应用更加普及。 一般形式为:

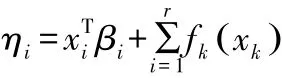
其中xi表示线性影响的解释变量观察值，xk表示非线性影响的解释变量观测值，βi表示模型的回归系数，fk( ·)是非参数解释变量的光滑函数。

3. 连接函数

通过连接函数将随机成分与系统成分连接起来，其表现形式为g(μi) ＝ηi。

通常模型结构如下:

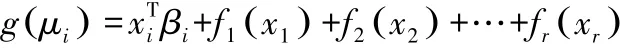
其中，μi＝E(Yi)，Yi服从指数分布族，fr是非参数解释变量的光滑函数。

三、 新疆维吾尔自治区地震损失模型实证分析

本文选取的实证数据为1990 ～2017 年期间发生在新疆维吾尔自治区的地震灾害事件(5.0 震级以上)，数据来源于《中国大陆地震灾害损失述评》《中国大陆地震灾害损失评估汇编》和中国地震信息网。 收集了1990 ～2017 年间共79 次地震灾害数据，数据包括了每次地震发生的时间、地点、震级和地震造成的直接经济损失。 在分析地震数据之前，需要将地震直接经济损失数据基于国内生产总值调整到2017 年的水平。

(一) 地震损失次数模型

损失次数是指在一个保险期间内，保单所发生的事故次数或索赔次数。 损失次数的取值为非负整数，可以用非负的离散型随机变量进行描述。

应用泊松分布、负二项分布和几何分布分别对新疆地区的地震损失次数进行拟合，其参数估计值和AIC 值如表1 所示。

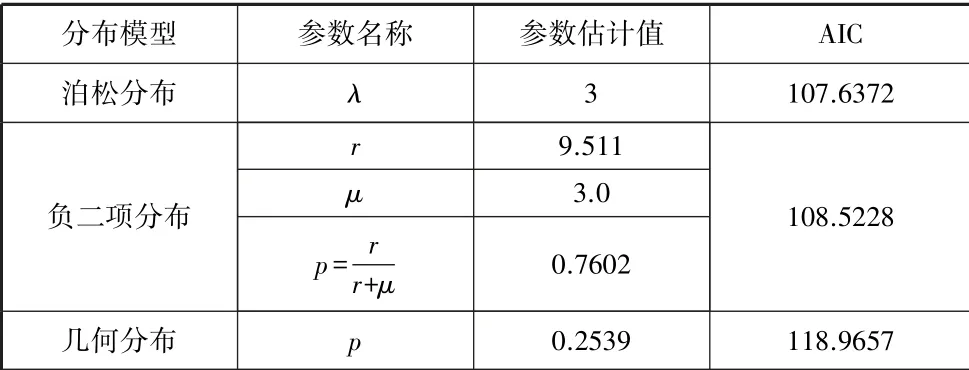
表1 损失次数的参数估计值和AIC 值

从表1 可以看出，泊松分布的AIC 值最小，因此泊松分布对每年的地震次数数据拟合的比较好，参数估计值为3。

(二) 震级分布模型

对新疆维吾尔自治区地震震级数据进行一个简单的描述性统计分析，发现新疆维吾尔自治区从1990 年至2017 年最大震级为8.1 级，如表2 所示。

表2 新疆维吾尔自治区地震震级数据描述性统计分析 (单位:里氏)

图1 为绘制的新疆维吾尔自治区震级直方图和密度曲线，纵轴是地震的震级，横轴是震级的密度，可以发现地震震级大多集中在5 级至6 级之间。

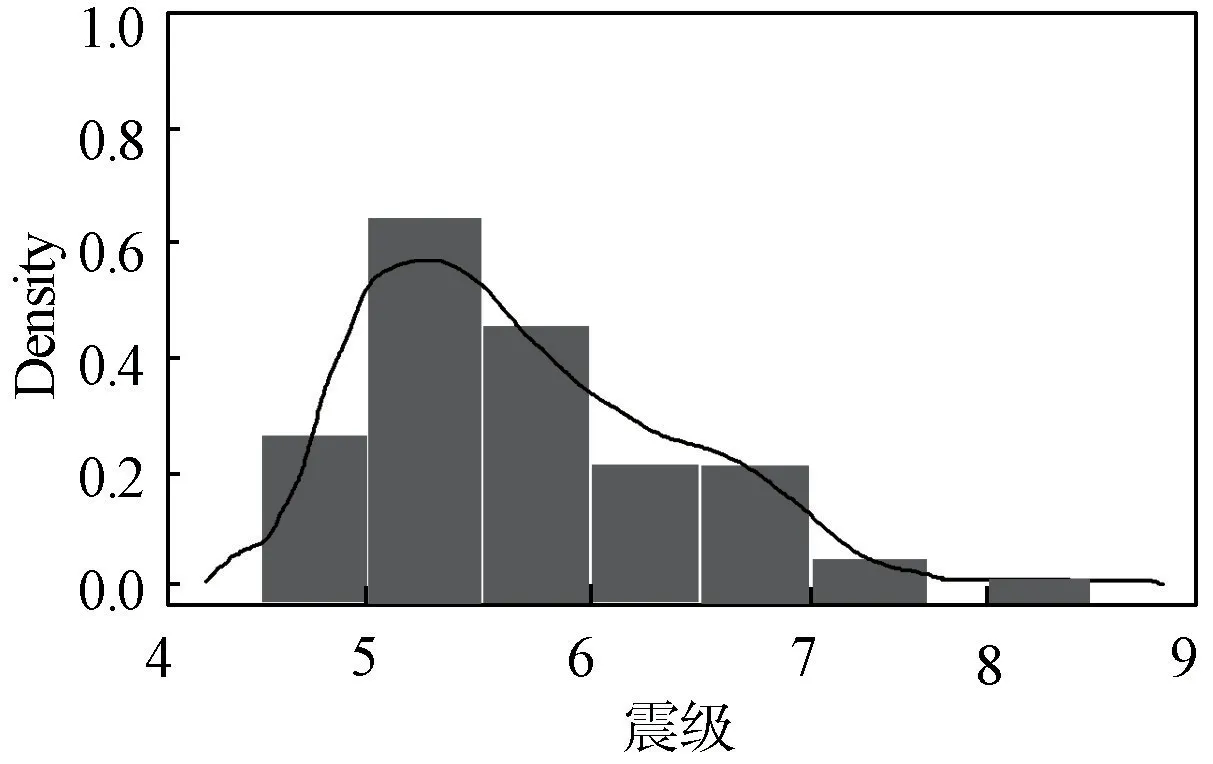
图1 震级直方图及密度曲线

从表2 和图1 可以观察出，新疆维吾尔自治区地震震级的分布具有尖峰厚尾的分布特征，可以尝试用广义帕累托分布、伽马分布、对数正态分布和韦布尔分布对地震震级的数据进行拟合，运用极大似然法估计模型参数的估计值，最后对各个分布模型进行KS 检验，如表3 所示。

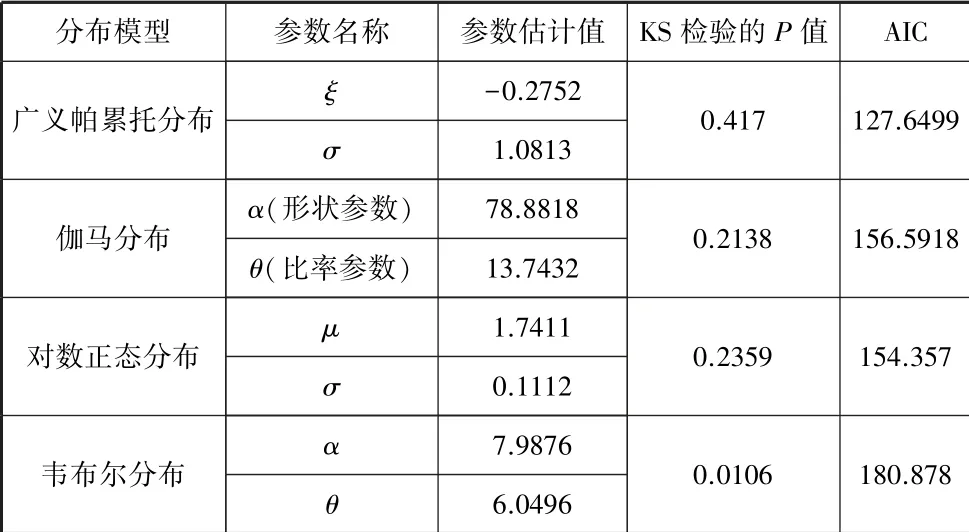
表3 震级分布模型的参数估计值

从表3 可以发现，广义帕累托分布模型、伽马分布模型和对数正态分布模型的KS 检验的P值都大于0.05，说明在95%的置信水平下不能拒绝样本数据服从于广义帕累托分布、伽马分布和对数正态分布；而韦布尔分布的KS 检验的P值大于0.01，说明在99%的置信水平下不能拒绝样本数据服从于韦布尔分布。 再对比四者的AIC 值，广义帕累托分布的AIC 值最小，因此选择广义帕累托分布对地震震级进行建模分析。

(三) 巨灾指数保险产品设计

1. 震级与经济损失的函数

地震自然灾害造成的经济损失与震级的高低一般呈现出正相关关系，震级越高造成的经济损失越大，震级越低造成的经济损失越小。 在地震震级与直接经济损失的近似函数关系中，以地震震级为预测变量，以经济损失为响应变量，建立广义可加模型，其模型的数学形式如下:非参数平滑函数，ε为残差变量。 其中把震级作为连续性变

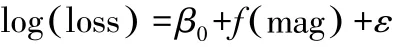
在上式中，loss 是经济损失，β0为截距项，f为震级对应的量进行平滑处理，使得模型拟合效果更好，同时给震级做平滑处理会使得模型的AIC 值减小。

震级与对数直接经济损失的散点图如图2 所示，可以看出震级与地震经济损失存在非线性关系。 右图是正态分布回归模型的AIC 值，在对数地震直接经济损失与震级的函数关系中，模型中对震级使用了三次样条平滑函数，绘制出自由度从1 至10 之间的AIC 值，可以发现在自由度为3 时，模型的AIC 值最小。

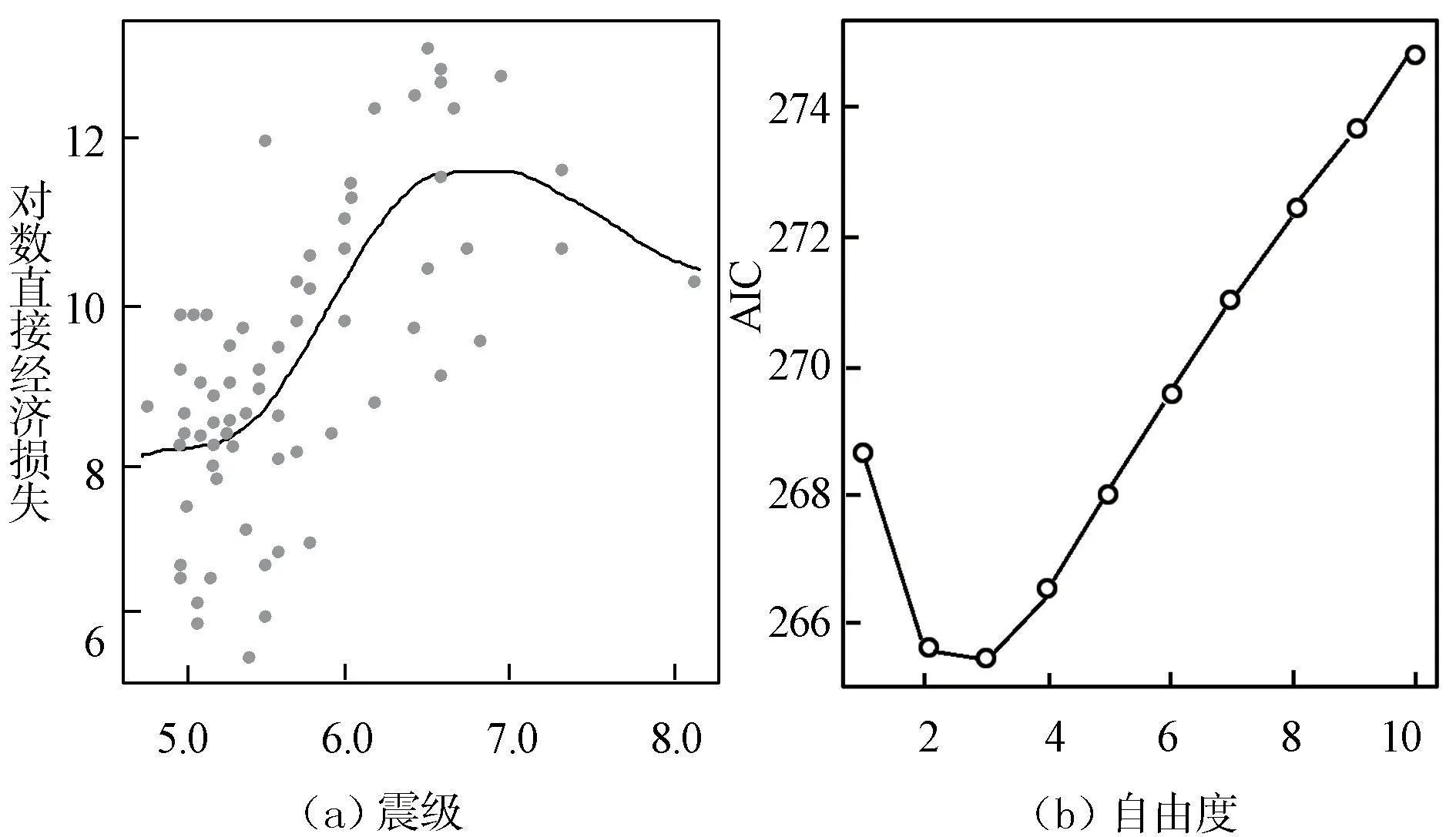
图2 震级与对数地震直接经济损失散点图和AIC 值

使用R 语言中的Gamlss 程序包中的Gamlss 函数建立对数地震损失与震级的正态分布回归模型，把震级作为连续性变量进行平滑处理，使得模型拟合效果更好。 给震级做平滑处理会使得模型的AIC 值减小。 图2(a)中的曲线就是对数地震损失与震级函数曲线的拟合值。

2. 震级指数分类

在本文中，震级一直作为连续性变量处理，现在为了把震级转换为一个合适的分类变量，引用R 语言中的Evtree 程序包，其中Evtree()函数是一种进化学习算法，它不仅提供了一个最优的分类和回归方法，而且在预测精度上具有更好的性能。 因此，再结合震级与经济损失之间的函数关系，探索出将震级转化为分类变量的最优区间端点。 由上文可知，对震级变量使用了三次样条函数，三次样条函数的自由度从1 到10 变化时，当自由度为3 时，模型的AIC 值最小，由此确定出震级与经济损失之间的函数关系。 如图3 所示，根据样条函数估计结果使用进化算法划分出最优分类的区间端点。 在表4中，列出了各个区间震级的频数。

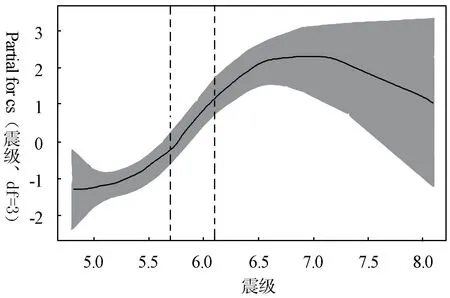
图3 震级指数分段区间

表4 震级指数分类区间频数表

从图3 和表4 可以看出，本文把新疆维吾尔自治区的震级划分为3 类，第一类震级是在4.8～5.7 级区间之内，从1990年至2017 年发生在一类区间的地震共有42 次，发生一类震级的概率大概为0.5455；第二类震级是在5.7～6.1 级区间之内，二类震级共有15 次，其发生二类震级的概率估计大概为0.1948；第三类震级是在6.1 级以上，共发生20 次，发生三类震级的概率大概是0.2597。

因为新疆维吾尔自治区从1990 年至2017 年间发生最高等级的地震是8.1 级地震，所以可以考虑把新疆维吾尔自治区的地震指数保险产品中震级指数的限值设定为8.5 级地震，超过这个保险范围保险公司只给最高赔偿限额。

3. 地震指数保险产品的纯保费

首先，根据不同类别的地震震级设定不同的赔付额度，表5 对各个震级类别的经济损失数据做了描述性统计分析，设定的赔付金额是根据大于各个震级类别的经济损失的均值。 第一类震级设定的赔付标准为15000 万元；第二类震级设定的赔付标准的50000 万元；第三类震级设定的赔付标准为200000 万元。

表5 各个震级类别的经济损失数据描述性统计分析 (单位:万元)

各个类别的纯保费的计算结果如表6 所示。

表6 地震指数保险产品的纯保费 (单位:万元)

四、 小结

相较于传统地震保险产品，地震指数保险更适应于当下保险市场的发展。 指数保险是为管理自然灾害风险而诞生的新型保险工具，在风险识别、风险评估以及风险转移方面起到重要作用。 虽然我国地震指数保险的发展相较于国际上许多发达国家较晚，但是我国已经具备发展地震指数保险的条件，地震巨灾指数保险的发展在我国未来可期。

结合新疆维吾尔自治区从1990 年至2017 年的地震灾害损失数据，构建地震指数保险精算模型。 在地震损失次数模型中，通过用不同的损失次数模型进行拟合，比较了模型的拟合效果，确定了每年地震发生次数服从泊松分布，均值λ＝3；在地震震级损失模型中，尝试了用伽马分布、威布尔分布、对数正态分布和广义帕累托分布对震级进行了拟合，通过对比发现广义帕累托分布对震级拟合效果最好；通过研究震级与经济损失的近似函数关系，建立经济损失与震级广义可加模型，并以此对震级指数进行分段处理，把震级指数划分为不同的区间，最后计算出不同类别震级指数的纯保费。

其次，根据本文建立的地震损失模型，地震指数保险产品的纯保费公式如下:类别震级所对应的纯保费；λ为地震损失次数的参数估计

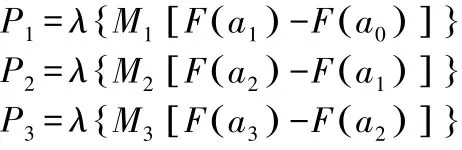
在上式中，P1、P2和P3分别为地震指数保险产品中不同值；M1、M2和M3是不同类别震级所对应的赔付标准；F(x)为震级的分布函数，震级服从广义帕累托分布；a0、a1、a2和a3是震级区间所对应的 区 间 端 点 。

震级的尾部分布函数数学形式如下:

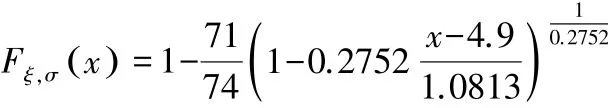
在理论上，纯保费是期望索赔频率与期望索赔强度的乘积，期望索赔频率是计算损失次数分布的均值，期望索赔强度是计算损失金额分布的均值。 但在地震指数保险产品中，要考虑到地震指数对纯保费的影响，由于指数保险的赔付依据是事先设定的参数是否达到触发标准，与实际损失金额无关。 使用地震震级的分布函数计算出震级区间的概率值，其中，一类震级的损失概率为0.4379；二类震级的损失概率为0.1607；三类震级的损失概率为0.2601，再与各类震级的赔付金额相乘得出的结果相当于期望索赔强度的值。 由于地震损失次数服从于泊松分布，均值为λ＝3，所以期望索赔频率的值为3。