基于迭代学习控制的二阶延迟微分系统研究

詹玉枝, 梁成斌, 张庆芳

(1. 贵州大学 电气工程学院, 贵州 贵阳 550025；2. 湖南大学 电气与信息工程学院, 湖南 长沙 410082)

1 引 言

生产生活中,诸多过程都或大或小存在延迟现象,例如在生产过程中,物料从一端输入,经过一些管道、或者传动带传输才能到达另一端,从而逐步被加工成产品,典型的应用有：轧机速度控制系统,炉温控制系统,发酵罐控制系统,造纸生产过程等[1～3]。延迟效应表现为当前状态变化不仅仅与当前的系统控制输入和状态相关,还依赖于过去某时刻的系统状态[4]。二阶微分系统在简谐振动过程总有大量应用。迭代学习控制技术最早由Uchiyama[5]和Arimoto[6]提出,是智能控制领域中研究、开发及应用的重要发展方向之一[7～10]。该方法采取在重复运行中根据迭代算法自动改进控制输入的策略来对系统进行控制,具有算法简洁、收敛速度快、适应能力强、易于工程化的优点。类比基本解阵对于常微分方程,文献[11]构造了二阶延迟微分方程的基本解阵：延迟矩阵正、余弦函数,并给出了其方程解的精确表达式。基于此,本文应用延迟微分系统的状态精确表达式,结合迭代学习控制的技术手段对二阶延迟微分系统的跟踪控制问题进行了研究。

介绍了二阶延迟微分系统的基本知识和其迭代学习控制问题的描述；分析了使系统输出收敛至期望输出的迭代算法收敛性；给出了仿真结果,验证了算法的有效性。

2 问题描述与算法设计

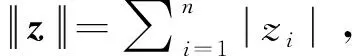
通过利用延迟微分方程显示解的表达式,考虑如下线性时不变迭代系统：

(1)

其中:A∈Rn×n非奇异,B∈Rn×r,C∈Rm×n,D∈Rm×r均为系统的参数矩阵；σ为固定的延迟效应延迟参数；T为一个固定的终端时刻。zk∈Rn为系统的状态变量；uk∈Rr为控制输入,yk∈Rm为系统输出；k为系统迭代次数，k=1,2；φ为延迟系统初始时间段系统状态,是二次连续可微的向量函数。

如式(1)所示的二阶延迟微分方程显示解的具体表达式已有研究结果[11],给出针对延迟微分方程基本解阵的两个定义及相关引理。

定义1[11]：延迟矩阵正弦函数sinσA(t):R→Rn定义如下：

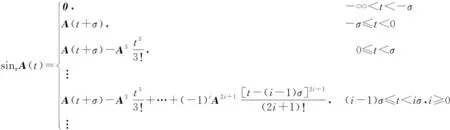
(2)

其中:0为零矩阵;σ>0表示延迟时间;i=0,1,2,…。

定义2[11]：延迟矩阵余弦函数cosσA(t)∶R→Rn定义如下：

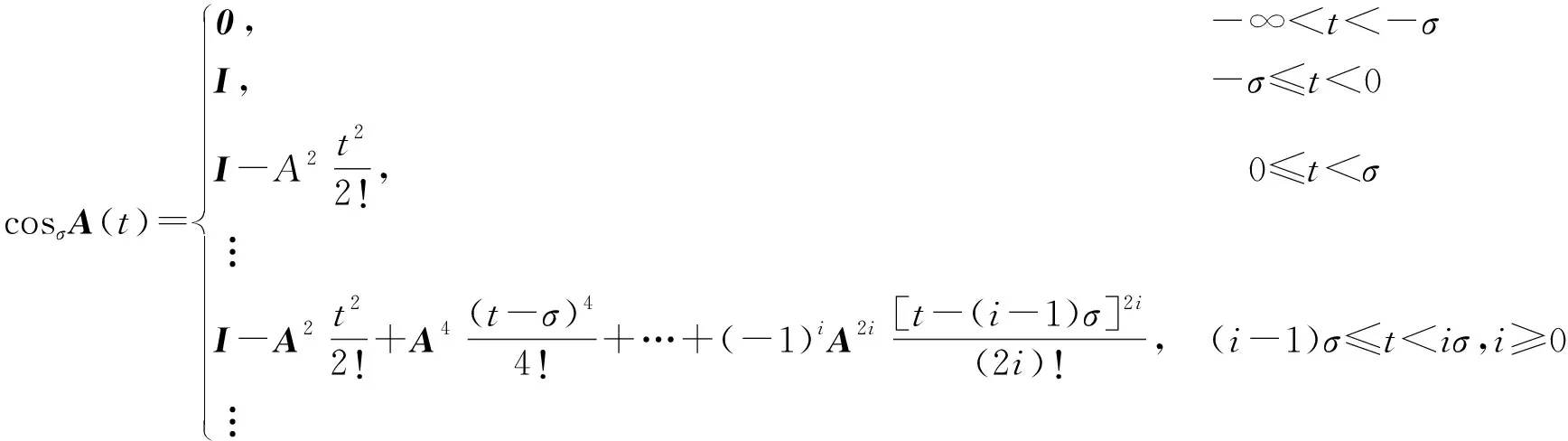
(3)

其中:I为单位矩阵;σ>0表示延迟时间;i=0,1,2,…。

引理1[12]:对任意t∈[-σ,+∞),如下范数上界估计成立：

(4)

(5)

图1 sin0.52t的函数图像Fig.1 Function image of sin0.52t

图2 cos0.52t的函数图像Fig.2 Function image of cos0.52t

如式(2)定义的延迟矩阵正弦函数sinσA(t)和延迟矩阵余弦函数cosσA(t)其实是矩阵正弦函数sinA(t)和cosA(t)的扩展形式,当延迟因子σ=0时,即不存在延迟现象时,延迟矩阵正、余弦函数退化成标准的矩阵正、余弦函数。图1和图2展示了延迟矩阵正、余弦函数sinσA(t)和cosσA(t)的一维函数图像。

其中ε是取决于实际情况的一个精度参数。

定义第k次和第k+1次迭代的输入增量为：Δuk(t):=u(k+1)(t)-uk(t)；系统的状态增量为：Δzk(t):=z(k+1)(t)-zk(t)；第k次输出误差为：

ek(t):=yd(t)-yk(t)

(6)

其中yd为期望输出轨迹。

针对式(1),考虑如下迭代学习算法：

uk+1(t)=uk(t)+L1ek(t)

(7)

其中L1∈Rr×m为需要进一步确定的可调参数矩阵。

根据文献[11],式(1)的系统状态可表示为：

(8)

继而,由式(8)可以表示出相邻两次迭代的系统状态增量为

(9)

3 收敛性分析

定理1：系统在学习算法的作用下,如果条件

(10)

证明：针对系统,根据式(1)可以得出任意相邻两次迭代误差的差值为

ek+1(t)-ek(t)=yd(t)-yk+1(t)-yd(t)+yk(t)

=-CΔzk(t)-DΔuk(t)

将迭代学习算法式(7)代入到上式中可得

ek+1(t)=(I-DL1)ek(t)-CΔzk(t)

(11)

对式(11)取范数,有

两边同时乘以e-λt,继而取λ-范数,得到

(12)

e-λt|Δzk(t)|

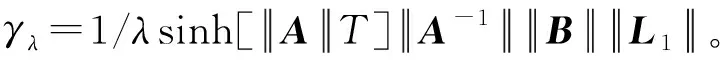
进一步,根据λ-范数定义,有

(13)

将式(13)代入到式(12)可以得出

(14)

在λ-范数中选取

由于任意两个范数在有限维空间上均是等价的,故在定理1中得到的结论针对于其它不同的范数定义也是适用的。

4 数值分析

考虑如下延迟系统的迭代学习控制：

(15)

其中：zk(t)；uk(t)=[u1k(t)；u2k(t)]T∈R2；Yk(t)∈R。

选取迭代学习算法式(7)如下：

uk+1(t)=uk(t)+[2,-0.4]Tek(t)

(16)

由系统式(15)和迭代算法式(16)知

通过式(8)可以得出系统式(15)的运行状态zk(t) 的相关情况如下：

当t∈[0,0.5)时,

当t∈[0.5,1]时,有

则系统每次迭代输出yk可由系统状态zk和系统输入uk表出。

算法实现：

步骤1：设置首次任意系统输入u1为零向量输入；

步骤2：根据式(8)计算第k次迭代的系统状态zk,并计算本次迭代系统输出yk=Czk+Duk及输出误差ek=yd-yk,k=1,2,…；

步骤3：根据学习算法式(7)生成第k+1次系统控制输入uk+1,更新步骤2,直至输出误差ek满足精度要求。

设置期望输出参考轨线为:

yd(t)=7sin(4πt)+4(t+0.5)2,t∈[0,1]

数值仿真结果如图3～图6所示。图3给出了系统输出对于期望输出的跟踪性能,展示出系统输出yk能够随着迭代次数k的增加(k=1,2,…,20)快速地收敛到预先设定的期望输出yd。

图3 期望输出与系统输出Fig.3 Desired output and system output

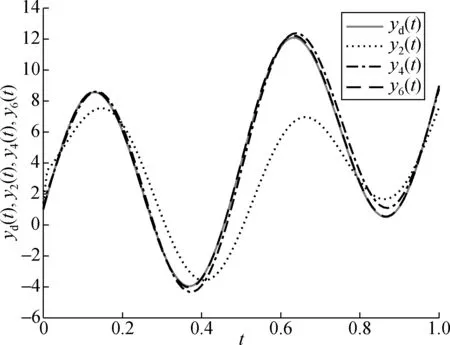
图4 期望输出与部分系统输出Fig.4 Desired output and part of system output

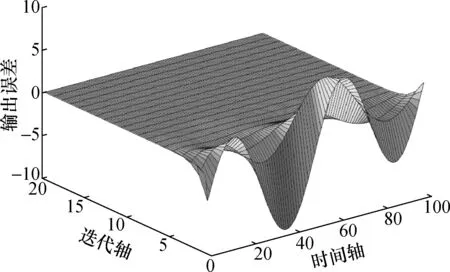
图5 输出误差三维仿真结果Fig.5 3D Simulation results of output error

图6 输出误差L2-范数Fig.6 L2-norm of output error

图4给出了部分系统输出y2,y4,y6与期望输出yd的函数图像,更清晰地展示出了系统输出能有效地随迭代次数增加而收敛到期望输出,验证了迭代算法的有效性。

图5是系统输出误差随着时间轴与迭代轴变化而变化的三维仿真结果。可以看出,随着迭代次数的增加,系统的输出误差在时间轴上的各个时刻都是趋向于0的。这表明了式(15)所示系统在迭代算法式(16)的作用下,随着迭代的进行,系统输出是收敛到期望输出的。

图6给出了系统每次迭代中输出误差的L2-范数的数值。可以看出随着迭代次数的增加,系统输出误差的L2-范数逐渐减小,收敛速度较快。可见,第20次迭代的系统输出误差为2.282×10-7,之后随着迭代的继续,系统还能继续自适应得出更优的系统输入,提高系统输出精度。

5 结 论

本文针对一类延迟微分系统提出采用延迟正余弦矩阵函数作为系统基本解阵,设计了系统迭代算法,用迭代学习控制的技术手段实现了对所提系统的自适应输出跟踪控制并迭代出相应的控制输入函数,对由延迟微分系统刻画的现实过程的有效控制具有指导意义。由仿真结果可知,随着系统迭代的进行,系统的输出误差逐步收敛至,即系统输出随迭代逐步追踪到期望输出,表明本文所提出的针对延迟系统的迭代学习算法是有效的。