基于技术授权的多市场古诺双寡头动力学分析

吴雪娇，李丹青

(兰州交通大学 数理学院，甘肃 兰州 730070)

近年来许多研究者对于技术授权问题做出了多方面的研究.技术授权不仅可以降低企业的生产成本，还可以提高产品的质量，使得企业在市场上形成一定的竞争力.为了追求利润最大化，李莹莹[1]，Stamatopolous和Tauman[2]，许治等[3]研究者在不同情况下对最适合同选择问题进行分析.事实上，关于技术授权的动力学行为研究相对较少.Aspremont和Jacquemin[4]首先将技术创新引入到寡头垄断的研究中，之后Kobayashi[5]开始关注寡头博弈的技术创新研究，Li和Wang[6]分析寡头垄断模式下的技术创新动态.

古诺双寡头博弈的动力学行为是复杂的，因为企业在每个阶段不仅要考虑自身的决策，还要考虑其他竞争企业的决策.在这里我们将这种博弈扩展到两个市场，不出所料，所得到的局部和全局动态结果十分丰富.由于研究者对于非线性双寡头垄断市场的兴趣日益高涨，使得企业的决策机制得到更新完善.在这一点上，罗琴和丁占文[7]，江小国[8]以及Ahmed[9]等提出了比较与企业使用naiïve期望更为现实的期望规则，假设企业在动态古诺博弈中表现出自适应行为，遵循一个有限理性的调整过程，且每个企业基于边际利润梯度规则更新投资策略.

本文将Zhao等[10]提出的模型进行拓展.引进技术授权问题的分析，在两个市场中，技术拥有企业作为生产性企业，它只对其中一个市场进行技术授权行为，且每个企业都有着相同的有限理性假设，基于边际利润遵循一个梯度原则，建立一个新的模型.特别地，利用Schur-Cohn判据对纳什均衡点进行局部稳定性分析，此外，为了揭示企业间竞争的复杂性以及该模型的内在复杂性，在数值模拟的基础上，利用混沌理论和分岔理论对系统进行分析.我们发现，这里存在一个调整速度的临界值，纳什均衡点将失去其稳定性.这个临界值还受到特许收费费用的影响，较大的特许收费费用更加有利于市场的稳定性.另一方面，在没有进行技术授权的市场中，可以推断，较高的不变边际成本确保纳什均衡点的稳定.

1 模型的建立

在古诺双寡头竞争市场中，两家生产性企业生产的商品近乎可替代但是在质量上有所不同，所以对于质量不同的商品，企业设定的价格也不同.假设企业之间进行产量竞争，且我们考虑市场A的逆需求函数：

pAi=ai-bi(qAi+qAj),(i,j=1,2,i≠j)

(1)

其中pAi表示在市场A中企业i的价格，qAi表示企业i的产量.ai>0,bi>0为常数.同样地，市场B的逆需求函数为：

pBi=mi-ki(qBi+qBj),(i,j=1,2,i≠j)

(2)

其中pBi表示在市场B中企业i的价格，qBi表示企业i的产量.mi>0,ki>0为常数.

假设企业1拥有能降低成本的新技术，企业1将对企业2进行技术授权.授权博弈包括三个阶段：第一阶段，技术持有企业作为Stackelberg领导者，为授权设定特许权收费费用r；第二阶段，其他企业扮演Stackelberg跟随者决定是否接受技术持有者的授权；最后一个阶段，2个企业在垄断市场中进行非合作价格竞争.不失一般性，假设企业2接受授权后，其边际成本降为零.在这篇文章中，我们假设企业1只在市场A中对企业2进行技术授权，且市场B的不变边际成本分别为cB.因此在市场A中企业i的利润函数分别为：

πA1=pA1qA1+rqA2,πA2=pA2qA2-rqA2,

(3)

其中r>0为企业2支付给企业1的单位产出费.市场B中企业i的利润函数分别为：

πB1=pB1qB1-cBqB1,πB2=pB2qB2-cBqB2.

(4)

我们可以得到企业i的总利润函数：

π1=πA1+πB1=(a1-b1(qA1+qA2))qA1+(m1-k1(qB1+qB2))qB1+rqA2-cBqB1,
π2=πA2+πB2=(a2-b2(qA1+qA2))qA2+(m2-k2(qB1+qB2))qB2-rqA2-cBqB2.

(5)

因此企业1和企业2分别关于市场A和市场B的边际利润如下所示：

(6)

(7)

其中常数α1,α2>0分别为市场A和市场B的调整速度.

2 均衡点及其稳定性分析

在Cournot双寡头市场中，企业1和企业2对产量决策经过多次反复的博弈，双方产量最终将达到一个均衡的状态，在均衡点处qi(t+1)=qi(t)，因此均衡点满足：

(8)

对方程组(8)进行求解，得到以下均衡点：

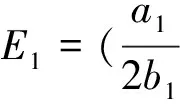
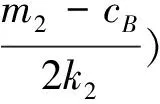
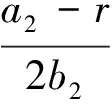
其中

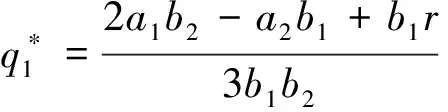
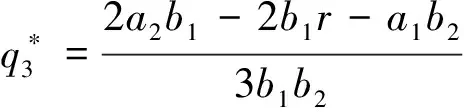
对系统(7)的均衡点进行局部稳定性分析，并得到以下结论.

由系统(7)可以得到其雅克比矩阵J为：

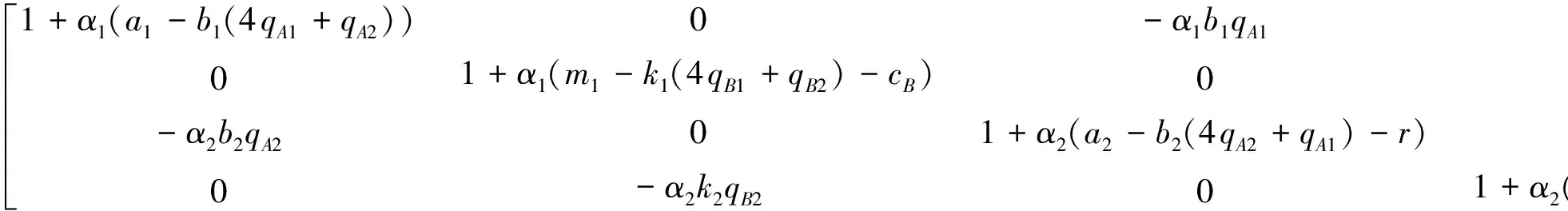
I)在E0=(0,0,0,0)处的雅克比矩阵J(E0)如下所示：

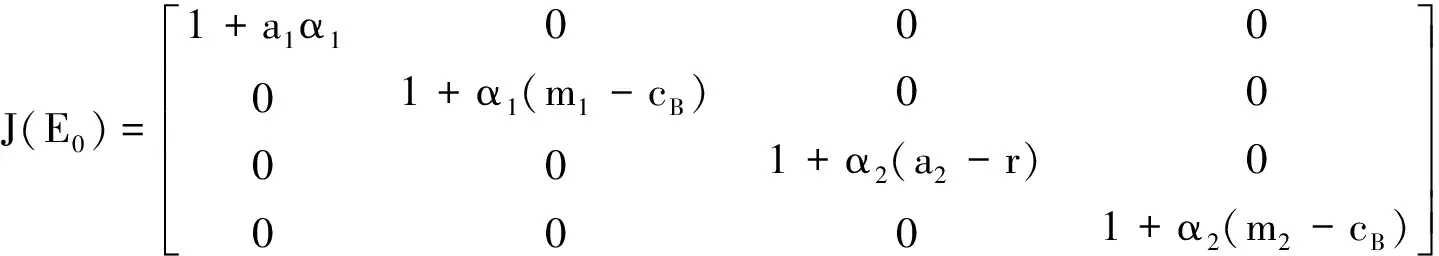
其特征值分别为：λ1=1+a1α1,λ2=1+α1(m1-cB),λ3=1+α2(a2-r),λ4=1+α2(m2-cB)，由于均衡点坐标有着非负性，αi>0,ai>0,a2>r,mi-cB>0,(i=1,2)，我们得到λi>1(i=1,2,3,4)，因此均衡点E0是不稳定的.

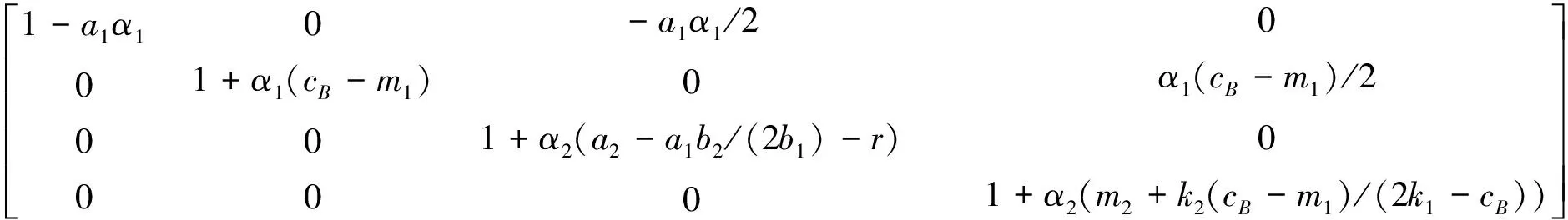
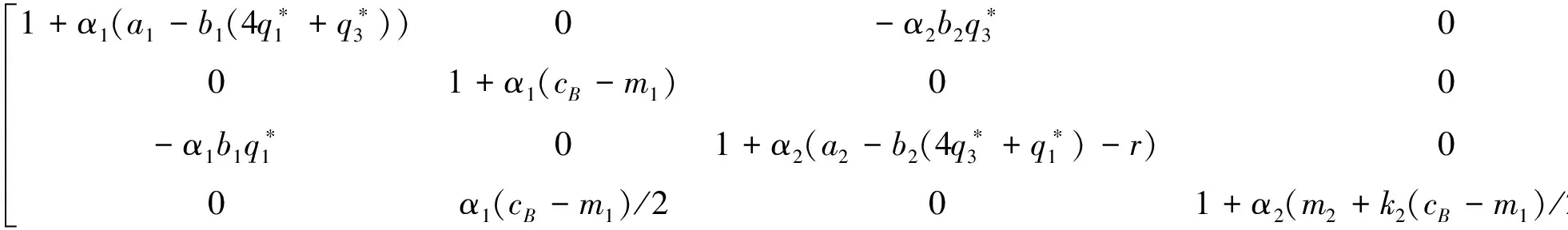
通过简单的计算，可以得到矩阵J(E11)的4个特征值：

其中

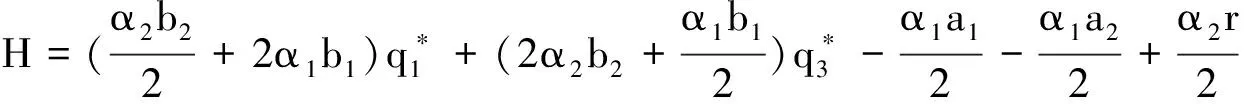
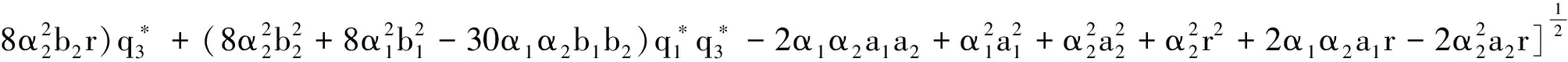
V)对于纳什均衡点E15=(q*1,q*2,q*3,q*4)的局部稳定性分析，由于在计算方面会更加复杂化，下面将利用Schur-Cohn判据对E15进行稳定性分析.

首先，在纳什均衡点E15=(q*1,q*2,q*3,q*4)处的雅克比矩阵为：

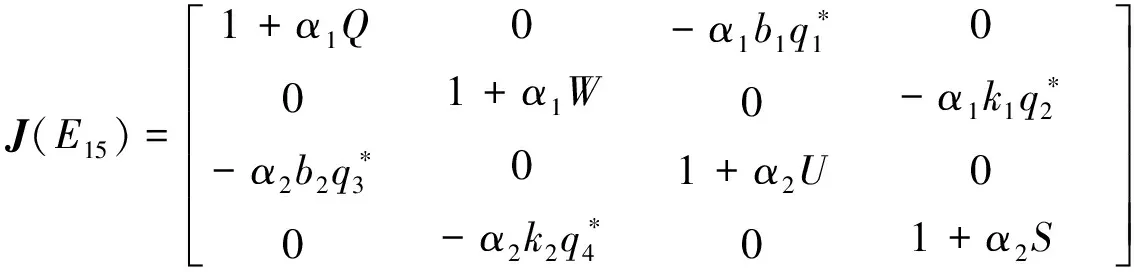
其中

Q=a1-b1(4q*1+q*3),W=m1-k1(4q*2+q*4)-cB,
U=a2-b2(4q*3+q*1)-r,S=m2-k2(4q*4+q*2)-cB.

特征多项式为：

F(λ)=λ4+A1λ3+A2λ2+A3λ+A4.

(9)

可以得到：

A1=-α1(Q+W)-α2(U+S)-4,

A2=QWα12+USα22+((WU+WS+QU+QS-b1b2q*1q*3-k1k2q*2q*4)α2
+3Q+3W)α1+(3S+3U)α2+6,

A3=((Qk1k2q*2q*4+Wb1b2q*1q*3-QW(U+S))α2-2QW)α21-2USα22+((Uk1k2q*2q*4+Sb1b2q*1q*3
-US(Q+W))α22+(2k1k2q*2q*4+2b1b2q*1q*3-2(WS+QS+QU+WU))α2-3(W+Q))α1-
3(U+S)α2-4,

A4=((b1b2k1k2q*1q*2q*3q*4-WSb1b2q*1q*3-QUk1k2q*2q*4+QWUS)α22+(QW(U+S)-
Qk1k2q*2q*4-Wb1b2q*1q*3)α2+QW)α21+((US(Q+W)-Uk1k2q*2q*4-Sb1b2q*1q*3)α22+
((W+Q)(U+S)-b1b2q*1q*3-k1k2q*2q*4)α2+W+Q)α1+USα22+(S+U)α2+1.

我们知道如果纳什均衡点是稳定的，那么它的特征多项式的所有根都在单位范围内，Schur-Cohn判据给出了充分必要条件：

i)F(1)>0,

ii) (-1)4F(-1)>0,

iii) 矩阵M±1和矩阵M±3的行列式都为正数，其中

因此，当特征多项式F(λ)的系数矩满足以下不等式组条件时，纳什均衡点E15是局部渐进稳定的，即：

(10)

3 数值模拟

上一章节我们对系统的局部稳定性做了一定的分析，为了更直观地分析系统(7)的动态行为，在这一章节我们以数值模拟方法继续对系统(7)在不同的初值条件下的动态演化过程进行可视化研究.具体地，研究内容主要分为3个部分：关于特许收费费用r与不变边际成本c分别作用于市场A和市场B长期动态结果的研究；初值条件问题.在这里我们用到的主要工具包括一维分岔图、二维分岔图、最大李亚普洛夫指数图、吸引盆等.

首先固定参数组a1=5.83,a2=3.56,b1=0.84,b2=0.42,α1=0.21；如图1～6所示，分别是r=0.1,r=0.2,r=0.25时在A市场中产量qA1,qA2关于调整速度α2的单参数分岔图以及对应的最大李亚普洛夫指数图.

从图1中发现，随着调整速度α2的不断增大，系统经历了flip分岔，从稳定状态变为不稳定，甚至是混沌.如图1(r=0.1)，当α2≤0.666 3时，市场中企业的产量轨迹是局部稳定的，接着发生倍周期分岔.这就意味着，对于较大的调整速度α2，决策者更不容易精准地掌握市场.

图1 当r=0.1时，关于α2的单参数分岔图 图2 最大李亚普洛夫指数图

图3 当r=0.2时，关于α2的单参数分岔图 图4 最大李亚普洛夫指数图

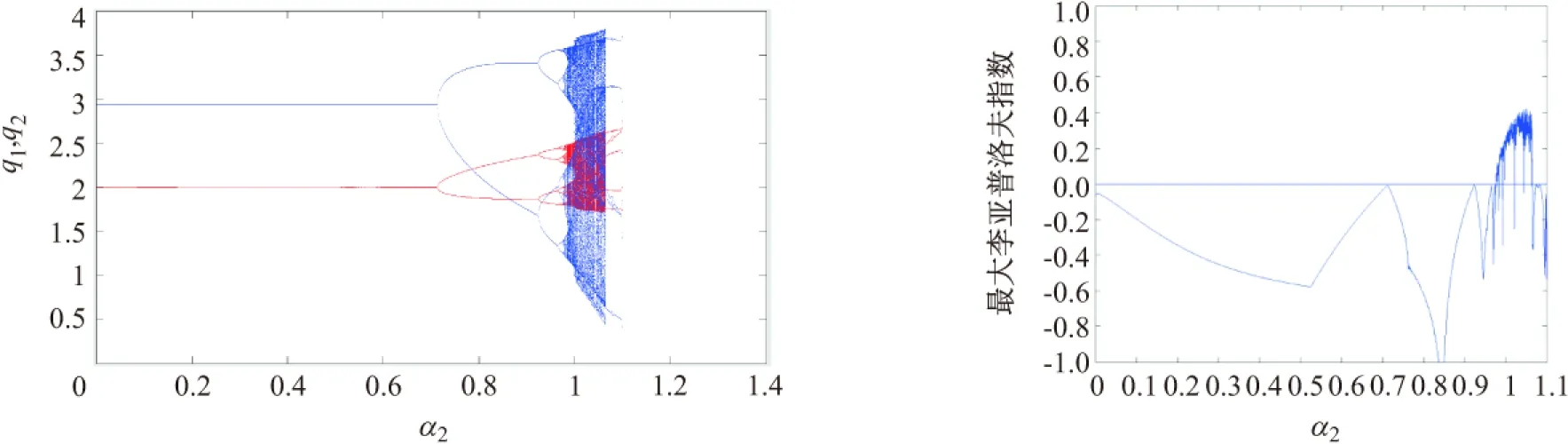
图5 当r=0.25时，关于α2的单参数分岔图 图6 最大李亚普洛夫指数图

随着r的增大，如图3(r=0.2)，当α2≤0.6965时，A市场中企业1和企业2的产量轨迹是局部稳定的，同样地，系统发生倍周期分岔失去其稳定性.如图5(r=0.25)，当α2≤0.7126时，A市场是局部稳定的.从上面的现象我们发现，较大的特许收费费用r能够让A市场变得更加稳定.

另一方面，考虑到市场A中特许权收费费用r=0.18以及调整速度α1=0.214,α2=1.06，参数a1,a2,b1,b2不变时，我们发现了2个不同的5周期吸引子共存现象，如图7为共存吸引子及所在吸引盆，其中深蓝色区域代表混沌区域或逃逸区域，浅蓝色区域为星状吸引子所在吸引盆，粉色为点状吸引子所在吸引盆.我们可以观察到这里的吸引盆存在明显的分形结构，与此同时，在大部分吸引盆中浅蓝色部分与粉色部分不能很好的分开.从经济学的角度分析，在市场博弈中，企业选择了略微不同的产量初值，将会带来很大不同的收益结果，在这种情况下，决策者也很难对市场未来进行一个精确的估计.当α1=0.216时，如图8，点状五周期吸引子变成了10周期吸引子，其中也出现明显的分形结构.特别地，点状吸引子所占面积增大.

图7 2个不同的5周期环共存的吸引盆 图8 1个5周期环和1个10周期环共存的吸引盆

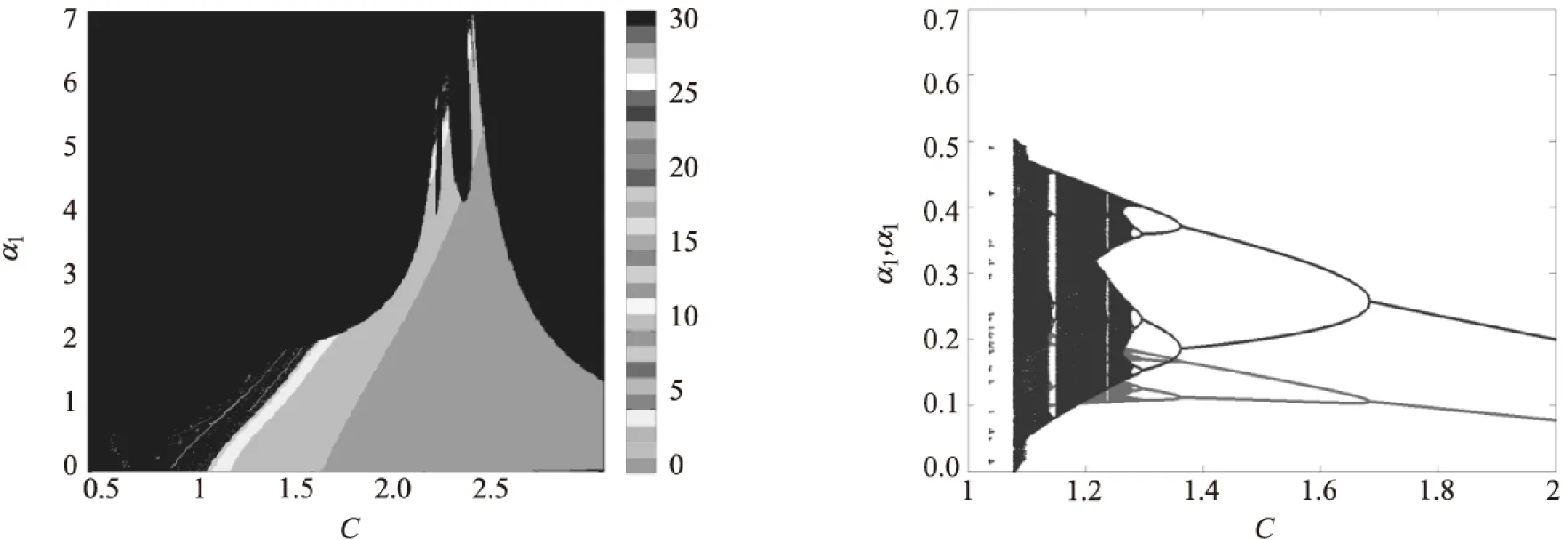
图9 α1与c的二维分岔图 图10 当α1=1.00时，关于c的单参数分岔图

接下来我们将对B市场进行研究，同样地固定参数组m1=2.98,m2=3.05,k1=2.76,k2=2.20,α2=1.60，同时，企业1的调整速度α1和固定边际成本c作为分岔参数.如图9我们将参数α1与c等分 1 000份，通过双层迭代算法绘制出关于α1与c的2-D分岔图，这种算法相对于传统的计算能够节约不少的时间.图10，当α1=1.00时，在市场B中产量qB1,qB2关于固定边际成本c的单参数分岔图，我们发现市场B对于较小的c是不稳定的，随着c增大，系统发生周期倍减分岔，从混沌状态到多周期的不稳定状态，再到稳定状态.这就意味着，随着不变边际成本c的增大，企业决策者对于B市场的预判是困难的.

4 结语

这篇文章分析了基于有限理性假设的多市场古诺双寡头博弈，其中A市场的2个企业进行了技术授权.利用非线性系统以及Schur-Cohn判据讨论了每个均衡点的局部稳定性.通过数值模拟为系统的复杂动态行为提供有力的证据，最主要的工具有一维分岔图，二维分岔图，最大李亚普洛夫指数图，吸引盆等等.首先，在一组固定参数组下讨论了特许收费费用r对A市场稳定性的影响，发现r在一定范围内的增大会让A市场更加稳定.在非线性系统中我们还发现了多重稳定性现象；对吸引子共存现象的分析，证明了初值条件对于系统的稳定性至关重要.最后，在一组固定参数组下讨论了固定边际成本c对B市场稳定性的影响，这里系统发生了周期倍减分岔，较小的c对于B市场的稳定是不利的.