深基坑新型支护结构变形控制的设计方案

蔡圳维 王维玉 王海龙

(1.河北建筑工程学院，河北 张家口 075000；2.河北省建筑科学研究院，河北 石家庄 050021)

0 引 言

随着国民经济的快速发展，城市的建设规模日益扩大，城市土地紧缺与土地扩大需求的矛盾也随之越来越大.于是人们为了寻求更大的空间，建设施工逐步从地面转入地下，地下空间工程向着规模大、开挖深度深、地质条件复杂的方向发展.同时，在国家提倡环保、节能的口号下，绿色建设施工已是重中之重[1].因此，在确保基坑安全稳定的前提条件下，绿色节能施工已然成为了讨论的主要话题.

桩锚支护结构是目前国内较常见的一种深基坑支护形式，由于其控制土体变形能力强、造价低廉、施工便捷、技术要求低等优势在深基坑工程被得到广泛应用.新型支护体系就是在借鉴桩锚支护结构优势的基础上进行改良的一种可全回收的支护体系.该体系是由多道竖向支撑桩、多道横向梁、挡土板及锚杆组成，与桩锚支护结构不同的是支护桩是由三层互相嵌套的空心钢管桩组成，待支护完毕后方便回收；可回收横梁是由多个型钢段构成，型钢段之间背对背隔开一段距离并用多个垫板焊接在一起；可回收挡土板可以插入两个型钢段之间的凹槽里，与上下横梁连成一个整体形成类似竖向挡土的整板；可回收机械式锚杆则是穿过横梁上相对应的垫板锚杆连接孔里进行锚杆端头锚固固定[2].综上所述，本新型支护体系不光施工操作便捷、材料可以重复使用，还减少了对环境的污染，实现了绿色施工.

本文将结合石家庄某深基坑工程，因地制宜地设计出一套切实可行的新型可回收支护结构初步方案，再通过数值模拟分析比较不同锚杆倾角、锚杆长度及土体强度等影响因素下新型支护结构的变形规律，对实际工程支护设计方案进行二次设计，即保证深基坑开挖过程中的安全稳定，又节约工程经济成本，提高施工效率.

1 支护桩和锚杆的设计计算理论

1.1 支护桩设计计算理论

单向弯曲梁抗弯强度计算公式：

(1)

(2)

式中：Mx、My分别是绕X轴和Y轴的弯矩(kN·m)；Wnx、Wny分别是对X轴和Y轴的净截面模量(m3)；γx、γy截面塑性发展系数，通过截面塑形发展系数表可查到圆环截面系数γx、γy均为1.15；f是钢材的抗弯强度设计值(N/mm2)；Kt是基坑支护的安全系数.通过选取Q235Φ600×15钢管来进行钢结构受弯梁计算，结果100.75 N/mm2≤112.64 N/mm2，抗弯强度验证符合设计要求.

抗剪强度计算公式：

(3)

式中：V为计算截面的作用剪力(kN)；Sw为计算剪应力处截面对中和轴的面积矩(m3)；Iw计算截面惯性矩(m4)；t为腹板厚度，圆管按管壁厚度计算(m)；fv是钢材的抗剪强度设计值(N/mm2).按照抗剪强度计算公式，得出计算结果62.30 N/mm2≤68.69 N/mm2，抗剪强度验证符合设计要求，因此确定选取Q235Φ600×15的钢管.

竖向桩设计计算理论详细参见文献[4]

1.1.1 支护桩受力示意图

图1.1 支护桩实际受力图 图1.2 支护桩计算简图

1.1.2 竖向桩的弯矩图和剪力图

图2.1 竖向桩弯矩图 图2.2 竖向桩剪力图

从两幅图中可以发现弯矩最大值和剪力最大值都分布在第四个间支撑点处，弯矩最大值是18.96kN·m，剪力最大值为389.41kN.因此竖向桩的危险截面位于10.5m处，所以将该点作为竖向桩的设计截面.按照竖向桩的设计计算理论公式确定选取Q235 FΦ600×15钢管[3].

1.2 锚杆设计计算理论

锚杆轴向拉力标准值：

(4)

式中：Nk是锚杆轴向拉力标准值(kN)；Fh为挡土结构的弹性支点水平反力(kN)；S是锚杆间的水平距离(m)；ba挡土结构宽度(m)；α锚杆倾角(°).

锚杆极限抗拔承载力标准值：

Rk=πd∑qsk,ili

(5)

式中：d是锚杆的锚固体直径(m)；li是锚杆的锚固段在第i土层中的长度(m);qsk，i是锚固体与第i土层的极限粘结强度标准值(kPa)，取值根据经验并查询规范表.

锚杆极限抗拔承载力与锚杆轴向拉力标准值的比值：

(6)

式中：Ks是锚杆抗拔安全系数，安全等级为一级的支护结构时Ks分别不应小于1.8，为二级时Ks分别不应小于1.6，为三级时Ks不应小于1.4；

锚杆设计计算理论详细参见文献[5]

1.2.1 锚杆设计尺寸

锚杆的设计按照传统拉力型锚杆进行设计，锚杆的水平间距为1.2 m，垂直间距为3 m，锚杆共四排，第一排距基坑顶部1.5 m，第四排距底部0.5 m，锚杆倾角取20°，成空直径为150 mm[5].锚杆按照设计规范的要求进行设计和验算最终计算结果如表1所示.

表1 锚杆设计结果

2 工程概况及地质情况

2.1 工程概况

拟建建筑场地位于河北省医院院内，工程基坑基础埋深11.0 m，基坑周长约200 m，场地地形较平坦.基坑东侧为道路和门诊楼，道路距离基坑下口线1.5 m，门诊楼距离下口线10.7 m；场地北侧、南侧、东侧周围地下管线在基坑支护施工前应停止使用并进行改造，保证基坑下口线10.0 m范围内无地下管线.场地其余部位无建筑物、地下管线等.基坑平面图如图3所示：

图3 基坑平面图

2.2 地质情况

拟建场地就处于滹沱河冲洪积扇上，位于河流南侧的Ⅱ级阶地上，地势平坦，微向南东倾斜，地面坡度1/1000左右.场内地势较平坦，勘探点相对高差0.51 m.根据钻探揭露及室内土工试验，结果表明对基坑支护有影响的地层主要为上部三层地层.主要特征如下：

(1)杂填土，主要由黏性土，碎砖块、灰渣、砼块等建筑垃圾组成，稍湿，松散.该层地基土层底埋深0.4～2.5 m，层厚0.4～2.5 m.

(2)黄土状粉土，褐黄色～浅黄褐色，稍湿，中密～密实，局部土质不均匀，含粘性土团块，无光泽反应，摇振反应中等，干强度低，韧性低.该层局部夹黄土状粉质黏土和粉砂薄层.该层地基土层底埋深3.1～5.8 m，层厚0.8～2.8 m.

(3)黄土状粉质黏土：黄褐色，可塑，切面稍有光泽，无摇振反应，干强度中等，韧性中等.该层地基土层底埋深6.1～11.6 m，层厚0.6～3.0 m.

本次勘察最大钻探深度45.0 m，未见地下水.地下水埋藏较深，可不考虑其对工程的影响.根据该区区域地质构造分析结果，该场地地基基底稳定性较好，适宜作为建筑场地.

依据场地地层岩性及分布可得其物理力学特性如表2所示：

表2 场地土层物理力学参数

3 数值模拟

3.1 计算模型建立

本模型采用有限元软件ABAQUS对新型支护结构进行分析.土体选取Mohr-Coulomb理想弹塑性模型，在确保没有边界效应的前提下，充分研究了基坑的具体形态特点、当地水文地质条件和新型支护结构影响范围等情况.该模型采用的是平面直角坐标系，x轴定为水平轴，y轴为垂直轴.模型底部定为固定约束，允许垂直方向发生变形；四周采用侧向约束，不允许发生水平方向位移；上表面为自由边界.采用Mohr-Coulomb弹塑性本构模型时，模型的水平长度和宽度一般取实际基坑开挖宽度的4倍，垂直高度取实际基坑开挖深度的3倍[2].考虑到基坑土体与周边环境具有对称性，因此为了方便模型计算，取实际基坑的四分之一部分来进行模拟分析，最后确定模型的尺寸长×高为280×35 m.

3.2 计算模型分析

数值模拟主要是分析比较不同锚杆倾角、锚杆长度及土体强度等影响因素下新型支护结构的变形规律，期望能对实际工程提出支护二次设计方案，在确保基坑安全稳定的前提下减少材料的浪费和污染.根据现场施工将基坑开挖分为4个工况，即第一步基坑由地表向下开挖1.5 m，然后布设第一层锚杆；第二步由坑底继续向下开挖3 m，然后布设第二层锚杆；第三步由坑底继续向下开挖3 m，然后布设第三层锚杆；第四步由坑底继续开挖3 m，然后在坑底以上0.5 m处设置第四层锚杆.由于基坑东侧所受的道路荷载和建筑荷载较大，变形位移较明显，因此取基坑东侧进行分析较为合适，基坑二维平面图如图4所示：

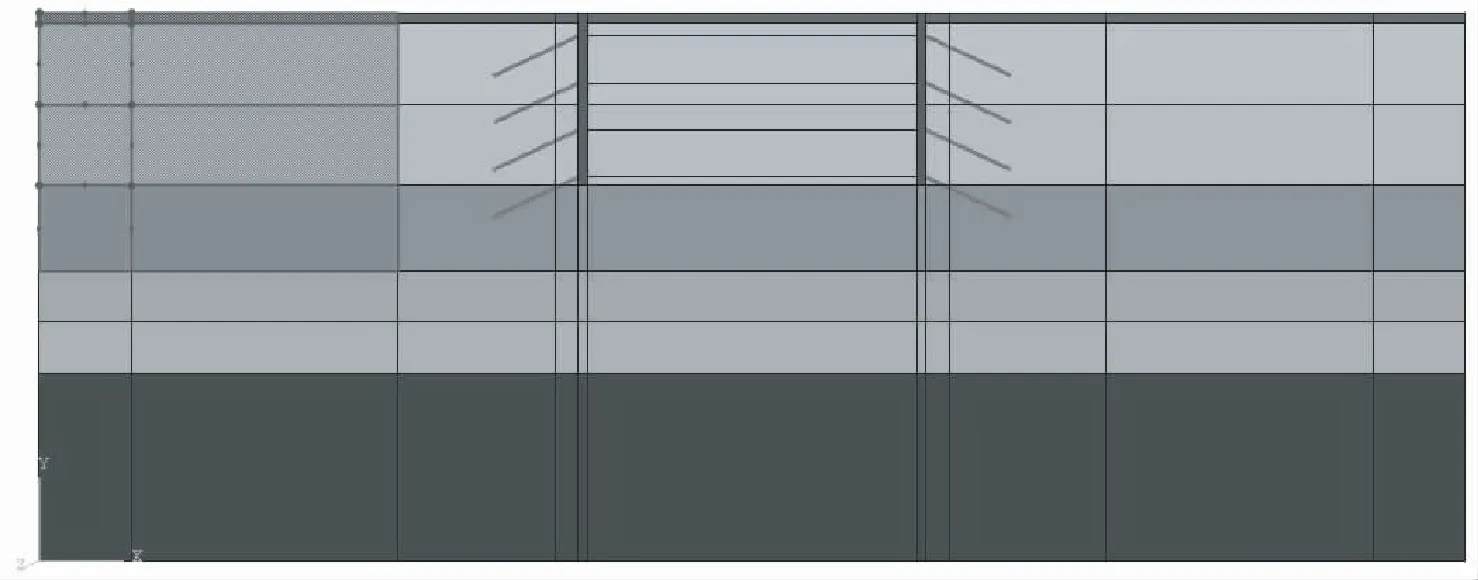
图4 基坑二维模型平面图

4 深基坑支护结构变形设计影响因素

4.1 锚杆倾角大小的影响

基坑开挖深度为11 m，在1.5 m、4.5 m、7.5 m、10.5 m的位置布设四道锚杆.在保证其他参数不变的情况下改变四道锚杆的倾角角度，分别取0°、10°、15°、20°、25°，支护结构水平位移如图5.1和5.2所示，图中横轴表示为x轴，竖轴表示为y轴(“+”表示向坑外的位移).

图5.1 锚杆不同倾角下的桩身水平位移 图5.2 锚杆不同倾角下的桩身最大水平位移

从图5.1中可以看出随着开挖深度的增加，支护桩变形呈现“凸拱”形状，当锚杆倾角为10°时，桩身变形曲线较大.锚杆倾角为0°、10°、15°、20°、25°时，桩身最大水平位移分别为83.4 mm、79.7 mm、61.8 mm、55.6 mm及57.5 mm，而且最大值基本都发生在桩顶以下6.0 m附近位置处.当锚索倾角为20°时，桩身最大水平位置最小，对支护结构最有利.因此可以验证锚杆倾角的不同会直接影响到支护结构的变形，在锚杆设计时应该优先考虑锚杆倾角问题，避免出现支护结构因倾角问题发生过大变形位移从而导致基坑的不稳定.

4.2 锚杆长度大小的影响

为探究锚杆长度大小对基坑新型支护结构变形的影响，对四道锚杆长度分别取6 m、8 m、10 m、12 m、20 m、30 m后进行模拟，支护结构水平位移变化规律如图6.1和6.2所示，图中横轴表示为x轴，竖轴表示为y轴(“+”表示向坑外的位移).

图6.1 锚杆不同长度下的桩身水平位移 图6.2 锚杆不同长度下的桩身最大水平位移

从图6.1和6.2中可以看出支护结构的变形与锚杆长短也有关系，随着锚杆长度的增加，支护桩的水平位移逐渐较小.锚杆长度为6 m、8 m、10 m、12 m、25 m、30 m时，对应的桩身最大水平位移分别是55.6 mm、37.6 mm、34.0 mm、31.8 mm、27.0 mm及22.4 mm.根据《建筑地基基础工程施工质量验收规范》GB 51004-2015提出的基坑的分类等级和基坑变形的监控值(mm)，规定一级基坑(开挖深度大于10 m)支护结构墙体最大位移不得超过50 mm[6]，因此当锚杆长度大于6.0 m时，支护桩的水平位移值均不超过规范标准值，.因此可以肯定锚杆长度的大小也直接影响了支护结构变形位移的大小，但这并不意味着锚杆长度越大越好，要恰到好处，在实际工程中锚杆设计时还是应该整体考虑，将模拟结果与现场监测数据相结合以寻找最合适的锚杆长度.

4.3 土体强度参数的影响

在保证其它条件不变的情况下，通过改变土体参数粘聚力与内摩擦角值分析新型支护结构变形规律，分别对两值同时增加20%、40%、60%，减小20%、40%，60%后进行模拟分析，结果如图7与表3所示，图中横轴表示为x轴，竖轴表示为y轴(“+”表示向坑外的位移).

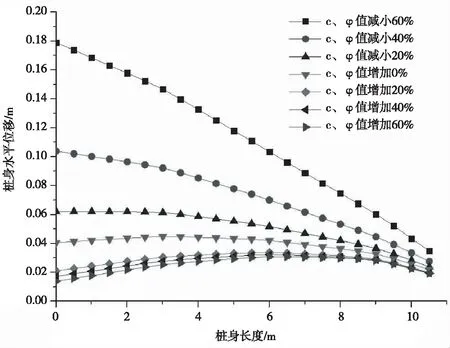
图7 土体强度的影响

表3 土体强度参数变化下的桩顶水平位移

从图7可以得知，随着c、φ值的不断增加，桩身水平位移开始减小幅度较大，越往后减小幅度慢慢减弱趋于一个稳定区间内.当减小c、φ值时，桩身水平位移增大幅度较快，待减小60%后，桩身最大水平位移达到了178.9 mm.但这仅仅是在模型时靠人为操作改变土体的粘聚力与内摩擦角，目的是验证土体参数对支护结构变形是否产生较大影响，在实际工程中还是应该通过地质勘探取得当地土岩地质参数.同时这也能说明土体会因为塑形变形、雨水侵入令土体中含水量增加从而导致土体强度大幅度降低，锚杆拉力减弱失效，最终使支护结构产生变形，影响基坑的安全稳定[7].从表3中可以看出，对土体强度增加20%后，支护桩的位移降低了大约48%，后续强度增加位移减小幅度并不大.因此可以认为在实际工程中适当提高土体强度，可以有效地控制支护结构变形，也证明了土体强度会影响到支护结构的变形，不能忽视.

5 设计方案

根据上述设计影响因素的模拟分析结果，再结合初始的新型支护结构设计，提出支护二次设计方案，初始方案与二次设计方案下桩体侧移变形对比结果如图8所示，图中横轴表示为x轴，竖轴表示为y轴(“+”表示向坑外的位移).当锚杆倾角为20°时，支护桩水平位移值最小，与初始设计锚杆倾角时相符合；锚杆长度设计取25 m时，支护桩水平位移为27.0 mm，二次设计后取锚杆长度为30 m，支护桩减少侧移变形17%，控制变形较明显；优化提高土体强度20%后发现支护桩的水平位移减小约48%，效果显著；初始设计中桩身最大水平位移值为32.4 mm，经过二次设计后桩身最大水平位移值为14.3 mm，比原先方案水平位移减少了约56%.证明采取二次设计方案后的新型支护结构内力得到重新调整，二次设计方案支撑布置比较科学合理.

图8 桩身水平位移设计对比

6 结 论

本文以石家庄某基坑为例，建立ABAQUS深基坑开挖过程有限元模型，对比分析了不同锚杆倾角、锚杆长度及土体参数等影响因素下支护结构变形规律，并对初始方案进行了二次设计，研究结论如下：

(1)锚杆倾角设计为20°时桩身水平位移最小，锚杆倾角设计为10°时，支护桩变形较明显，15°～25°对应的桩身水平位移都在可控范围内，当锚杆倾角设计小于10°时，支护桩水平位移远远超过基坑规范变形值，可能会影响基坑整体安全稳定.

(2)通过增长锚杆长度可以发现桩身水平位移有了明显的减小，说明锚杆长度直接影响了支护桩水平位移.但并不代表可以随意加长锚杆长度，必须控制在锚杆长度规范设计的标准内，模拟只是为了发现规律，为实际工程提供指导意义，锚杆长度设计还是应该结合工程具体情况来操作.

(3)土体强度的变化首先会影响到锚杆的拉力间接导致支护桩发生位移.当土体强度增加20%后桩身位移明显减小，再通过加强土体强度的办法来减小桩身位移后发现位移减小幅度不大.因此，在实际工程中必须预防土体发生塑形变形，适当的增强土体强度来减小围护结构的位移从而保证基坑的安全.

(4)该新型装配式可回收支护体系可以达到支护桩、板、梁以及锚杆全部回收，因此在锚杆的选择上可以考虑适当加长锚杆长度来保证深基坑的整体安全稳定性，待钢绞线回收之后重复利用2～3次便可基本抵消锚杆增加长度时所产生的材料费用，这样就使新型支护结构二次设计方案比初始方案更安全可靠，经济合理，使深基坑开挖支护施工更加科学.