下垂控制微电网的无功补偿失稳机理及抑制对策
施云杰 冯夏云 汪 飞 张笠君 李玉菲
(上海大学自动化系上海市电站自动化技术重点实验室 上海 200044)
1 引言
由于下垂控制逆变器广泛应用于微电网中,故有学者认为基于下垂控制的微电网实为基于改进下垂控制的UPS 集群[1]。下垂控制应用于微电网的研究大致可分为两类:如何提升下垂控制的动态响应[2-4]及如何改善下垂控制有功、无功功率均分性能[5-8]。考虑微电网线路的经济运行、传输损耗等因素时,用户的功率因素要求大于0.85,从而使得微电网这类低压配电网的无功传输限制在较低水平[9-10]。因此,就改善下垂控制的功率均分性能而言,无功功率均分性能远没有功功率均分性能重要。但诸如电机这类感性负载将不可避免地广泛存在于微电网中,从而使得微电网的无功补偿至关重要。
在传统电力系统中,基于智能无功补偿电容器及电力电子静止无功补偿器组合而成的混合无功补偿设备被视为高性价比的补偿方案[11-14]。这类设备通过智能开关无缝投切电容器组,实现无功功率的实时补偿,通过采用电力电子静止无功补偿设备,实现无功功率的动态无级调节。由此可见,未来数十年内微电网将像传统电网一样,大量采用无功补偿电容器组进行无功功率补偿。无功补偿设备引入微电网后诱发的失稳问题,同样也得到了广泛的关注,对于电力电子静止无功补偿设备入网诱发的微电网稳定性问题,可以通过调整无功补偿设备的控制参数或采用谐振抑制策略得以解决[15-18]。然而,由无功补偿电容器诱发的孤岛微电网失稳问题,却无法像电力电子无功补偿设备可主动实现谐振抑制,这是目前诸多研究所欠缺的。
综上所述,本文将研究无功补偿电容器诱发的下垂控制微电网稳定性问题。首先,采用小信号建模法构建了下垂控制逆变器的输出阻抗,揭示了下垂控制仅影响逆变器输出阻抗的低频特性。因此,分析由下垂逆变器输出阻抗高频外特性引发的谐振问题时,可忽略下垂功率环。其次,在忽略逆变器的下垂功率环后,采用阻抗稳定性判据分析了下垂逆变器构成的孤岛微电网引入无功补偿电容器后的谐振稳定性问题,揭示了下垂孤岛微电网引入无功补偿电容后的谐振问题,并提出在电流内环中引入电容电流反馈控制,重塑逆变器输出阻抗,抑制谐振,提升微电网的稳定性。最后,本文设计了一台3 kW 的样机,进行了下垂微电网的无功补偿试验,验证了本文所提有源谐振抑制算法的有效性。
2 下垂控制逆变器输出阻抗外特性
2.1 下垂控制基本原理
下垂控制的基本思路源自于传统电力系统功率传输特性[19]。如图1 所示当发电端通过感性传输线对负载供电时(线路阻抗为,系统的有功功率Pi、无功功率Qi传输特性如式(1)所示。其中,Ui、U 分别为逆变器输出电压幅值及负载电压幅值,逆变器输出电流幅值 Ii= U /XL。ZLoad为负载阻抗(由有功负载RLoad及无功负载XLoad组成),θi为逆变器的输出功角,定为分为逆变器输出电压的角频率及负载电压的角频率。由于功角变化较小,因此由式(1)便可实现P-ω,Q-U 的近似解耦控制。不失一般性,本文以式(2)所示的下垂控制为例进行研究。其中m、n 分别为下垂控制逆变器的有功和无功下垂系数,Eiref、ωiref分别为逆变器输出电压幅值参考及频率给定参考。
下垂控制逆变器系统如图2a 所示,基于式(2)所示下垂控制的下垂逆变器系统结构框图如图2b所示,逆变器参数如表1 所示。ui、ii分别为逆变器输出电压、电流值,pi、qi分别为逆变器瞬时有功功率及瞬时无功功率。
本文将下垂逆变器的输出电流后接入如式(3)所示二阶广义积分器(Secondary order general integral,SOGI),得到两相正交电流,并与电压相乘,得到有功瞬时功率pi、无功功率瞬功率qi。将pi、qi通过一阶低通滤波器F(s),滤除其中两倍频的脉动功率,得到Pi、Qi。通常一阶低通滤波器带宽比电网频率小10 倍频程[21],本文选取截止频率5 Hz。
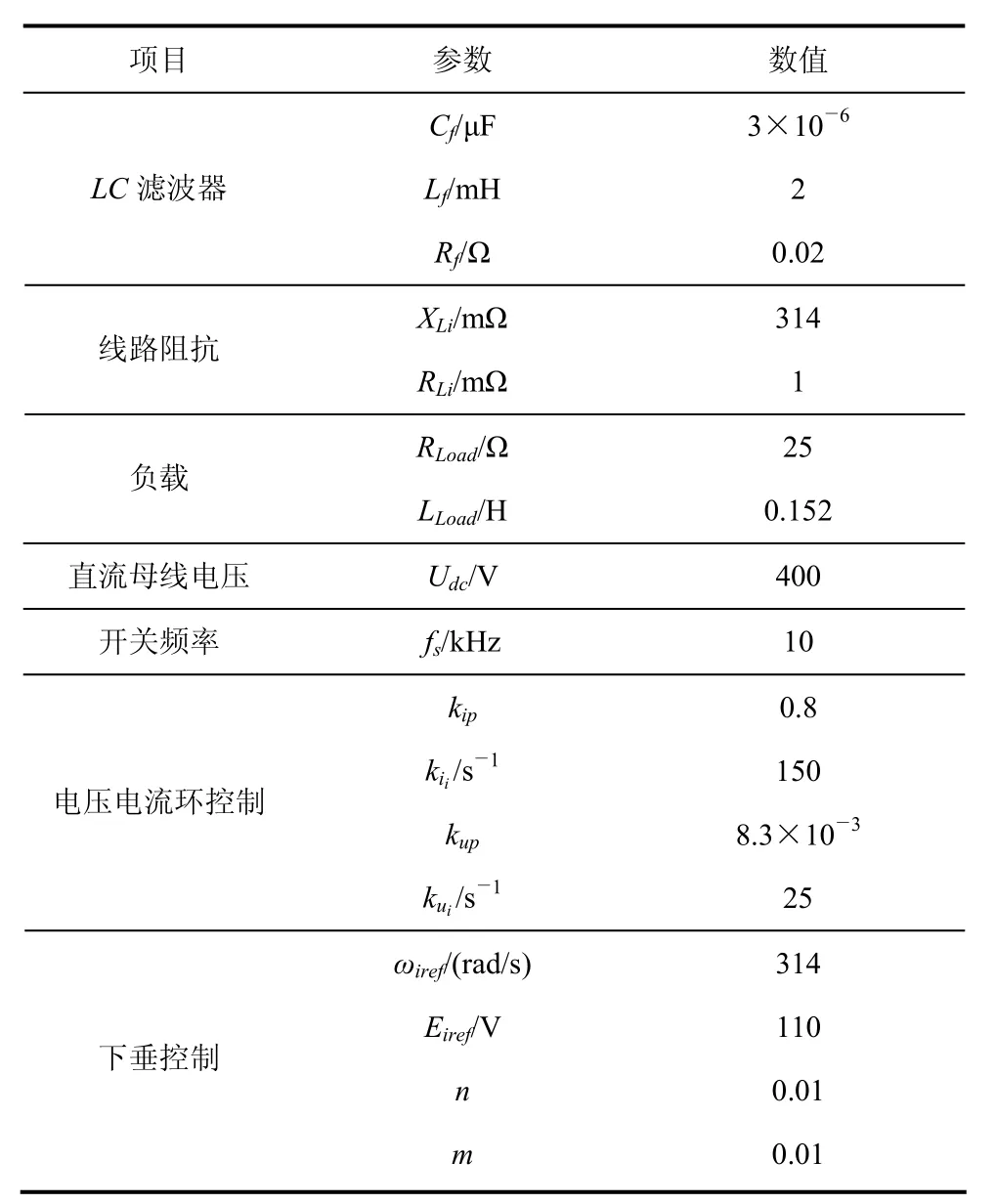
表1 系统参数
2.2 下垂控制逆变器输出阻抗建模及分析
为研究电容器无功补偿下微电网的稳定性问题,本文首先建立了下垂控制逆变器输出阻抗外特性模型。由图2b 所示的框图,可求得下垂控制逆变器的简化模型,如图3 所示。其中传递函数Gclose及输出阻抗式Zo如式(4)所示。
考虑下垂功率控制环,列写式(5)
采用小信号分析法,对式(2)及式(5)进行线性化,得式(6)。同时,由式(6)可解得下垂控制逆变器输出阻抗Zo_Droop如式(7)所示。
对比分析Zo及Zo_Droop的零极点图4a 可知,下垂功率控制环将使Zo_Droop中引入近似成对的非主导零极点,高频零极点近似互消使得下垂控制功率环对下垂控制逆变器输出阻抗Zo高频段阻抗影响较小。因而,P-ω 控制参数m 及Q-U 控制参数n 主要影响下垂控制逆变器的输出阻抗低频外特性。以Q-U 控制参数n 对Zo_Droop频率特性的影响为例,Zo_Droop的低频段阻抗值将随n 的增加而软化,如图4b 所示。
3 基于阻抗的无功补偿谐振稳定性 分析及抑制方法
3.1 下垂控制逆变器无功补偿稳定性分析
根据文献[22]所提出的级联系统的输出阻抗稳定性判据,对如图5a 所示级联系统分析。
引理:定义输出阻抗Zout及输入阻抗Zin,当Zout与Zin满足以下条件时:(a)>6 dB;与°系统保持稳定。以图5b 所示系统为例进行说明,Zin相位在区域1 处进入阻抗禁止域内,因此系统不 稳定。
当图1 所示孤岛微网系统进行无功补偿时,负载侧并联无功补偿电容器。根据引理分析其稳定性,如图6 所示。其中Zout为第2 节中基于下垂控制逆变器输出阻抗Zo_Droop的频率特性曲线,Zin为RL 负载并联无功补偿电容C 后的等效阻抗频率特性曲线,参数如表1 所示。当|Zin|-|Zout|小于6 dB 时,相位不满足条件(b)的禁止条件,故系统不稳定。
3.2 谐振抑制方法
无功补偿的引入使得下垂孤岛微电网丧失稳定性,因此需要采用一定的谐振抑制策略,使系统重新趋于稳定。本文分别研究了无源阻尼法与有源阻尼法[23-26]。首先,本文提出如图7a 所示的无源阻尼法,在电容Cf两端并联电阻Rd。随着Rd阻值减小,逆变器输出阻抗减小,从而使得Zo_Droop的相位也随之变化,如图7b 所示。而Zo_Droop相应的禁止域也随之发生改变,使得加入无功补偿电容器后的负载阻抗相位避开阻抗禁止域,从而改善系统失稳风险,如图7c 所示。 但Rd的减小将增大其功率消耗,降低系统效率。为克服无源阻尼法的缺点,本文又提出基于电容电流反馈控制的有源阻尼抑制策略,实现逆变器的输出阻抗重塑,如图8a 所示。此时,双闭环控制逆变器输出阻抗Zo_act为
突变年后即1981-2014年F(n,k)计算结果见表2。绘制目标函数 F(n,k)~k 和非负斜率 β(k)~k曲线如图3所示。由图3可知使β(k)最大的k值为k=3,则k=3为最优分类数,对应表2,当k=3时,汛期分期结果为1-3,4-12,13-17,即前汛期是从6月15日至6月30日,主要汛期为7月1日至8月15日,后汛期8月16日至9月10日。
令Zo=Zo_act,并代入Zo_Droop中,即可求得引入电容电流反馈控制后的下垂控制逆变器输出阻抗。分析Rdc对输出阻抗Zo_Droop频率特性的影响,如图 8b 所示,此时发生阻抗重叠处的阻抗值相比无源阻尼抑制法而言,得到了进一步削减。因此,避免了无功补偿电容接入时的阻抗交叠,使得负载阻抗避开了禁止域,提高了系统稳定性,如图 8c所示。
4 试验验证
本文搭建了单微源微网,参数如表1 所示。电网负载为25 Ω 的阻性负载与0.152 H 的感性负载。此时,逆变器输出电流滞后电压,如图9a 所示。随后,负载侧接入32 μF 的无功补偿电容,逆变器输出电压、电压发生振荡,系统谐振失稳。为了抑制振荡,本文引入第3.2 节所述的基于电容电流反馈控制有源阻尼抑制策略,试验结果验证了本文所提谐振抑制方法的有效性。如图9b 所示。
5 结论
无功补偿对基于下垂控制的孤岛微电网十分重要。考虑无功补偿成本,未来仍会采用无功补偿电容器配合电力电子静止无功补偿设备的组合形式,实现实时、无级的无功补偿。但采用电容器进行无功补偿时,微电网容易产生谐振问题,从而丧失稳定性。为了抑制谐振,本文提出在电流内环中引入电容电流反馈控制,实现下垂控制逆变器输出阻抗重塑,从而使得系统恢复 稳定。

