立足数学核心素养的课堂教学
——以《对数函数(第1课时)》的教学为例
白 彬
(安徽省宿州市第二中学 234000)
一、教学目标的制定要凸显数学核心素养
教学目标:
1.理解对数函数模型所刻画的数量关系,以此提高学生对数据的运算、分析处理能力和抽象概括能力,掌握对数函数的研究方法,培养学生将实际问题转化为数学模型(数学建模)的能力.
2.通过分析进一步揭示对数函数概念的实质,培养学生研究问题的意识,建立数与形的联系,理解对数函数的图象与性质.
教学重点:对数函数性质的理解与应用.
教学难点:体会对数函数是一类重要的函数模型(概念、性质、研究方法),并运用性质解决问题.
二、教学活动的设计要立足数学核心素养
教学过程:
1.引入概念
问题1:n=2m,当n为已知量时,m=?即m=log2n.
设计意图:引导学生在明晰运算对象的基础上,依据运算法则解决数学问题,不断提升其数学运算素养.
问题2:n与m之间在对数运算作用下,是否可以建立函数关系?
设计意图:在对数运算的作用下,m=log2n(y=log2x)形成从正实数集到实数集的一一对应关系.在课堂上呈现过程中,通过离散取点到慢慢连续的过程,促成学生从感知到一种理性的认识.
设计意图:建立形与数的联系,利用几何图形描述,借助几何直观理解问题,形成数学直观;教师可适当介绍对数函数发展的历史,加深对函数概念本质的认识和理解.
2.探究性质
对数函数进一步的研究(对性质的思考)
问题1:通过上面两个具体的对数函数,能对一般的对数函数的性质有哪些猜想?
总结概括:解析式:y=logax(a>0且a≠1),定义域:(0,+);值域:(-,+);奇偶性:非奇非偶;过定点:(1,0);
图象:
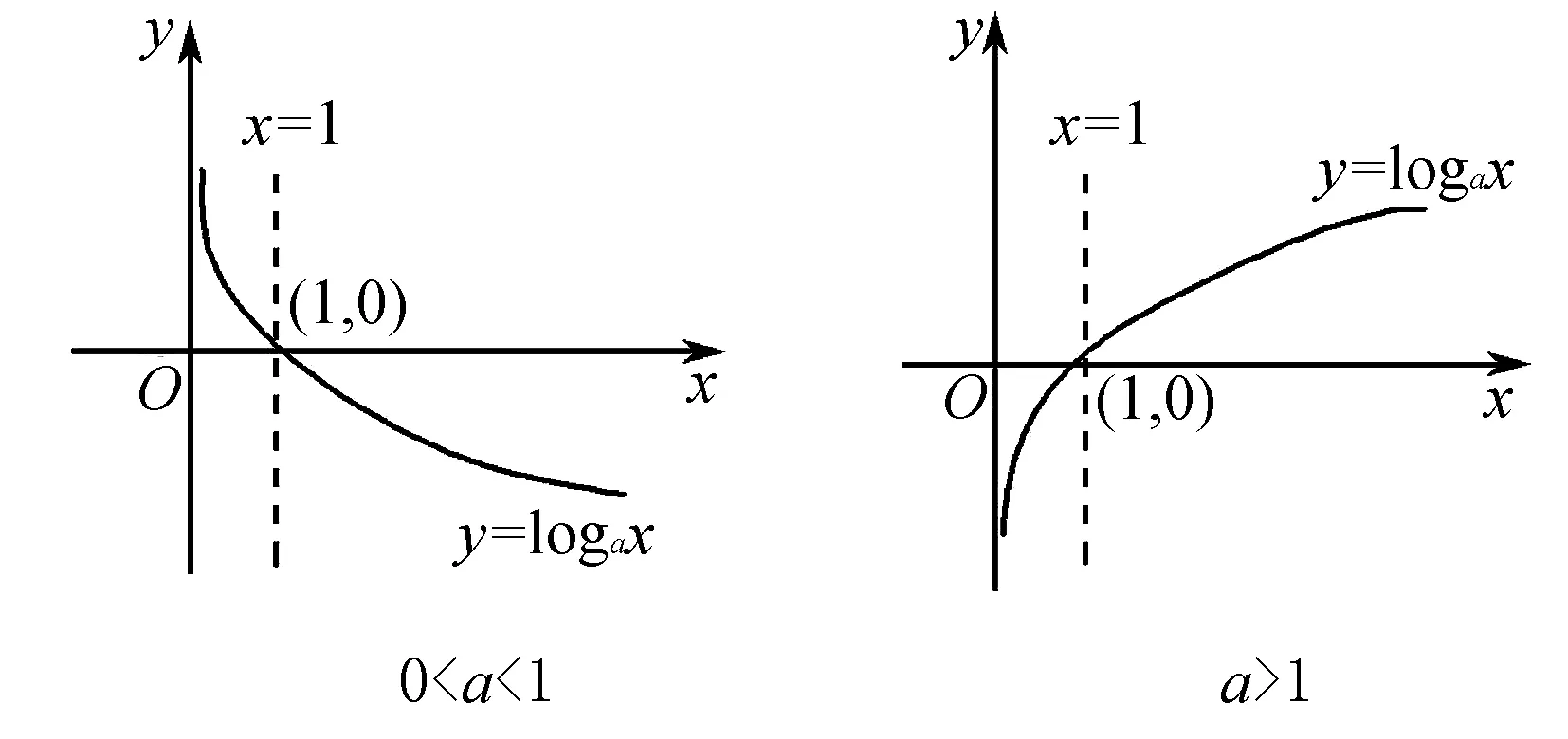
设计意图:引导学生将函数图象的特征以及图象的变化趋势几何直观地描述转化为文字语言、数学语言的描述,提高学生的数学素养.
问题2:通过什么方法得到这些猜想?我们如何得到对数函数单调性呢?能否给出恰当的证明?
设计意图:高中知识已经学习了单调性和奇偶性的定义了,是有可用的工具来完成单调性的证明,不能只相信直觉和直观了.
角度一:根据对数函数与指数函数的关系(运算之间的相关关系)
①当0
角度二:根据对数运算的性质(运算律)
设计意图:精心设计适当的情境、活动,如是下去,夯实基础,强化基础,提高能力,发展素养就不会只是一种教学上的“追求”!
3.应用(例题选取、讲解要渗透数学核心素养)

问题1:求给定函数的定义域是一个什么问题?函数性质的研究方法是什么?

设计意图:以问题为驱动力,并将几个要点分散到题目中,有利于学生掌握函数的研究方法,以及方程、不等式在研究函数中的作用.
例2已知log0.7(2m) 设计意图:解决变量的问题,本质上就是研究其对应函数性质. 4.课堂小结(围绕以下几点展开) (1)函数的研究就是获得具体和一般的函数的性质的过程; (2)函数的研究方法与函数的三种表征紧密关联; (3)函数性质的研究需要方程和不等式的运算,同时在方程和不等式的求解问题中可以运用函数的性质. 设计意图:教师在课堂教学中应逐步引导学生会学数学:①会数学阅读;②会质疑反思;③会梳理总结;④会表达交流.这些都是数学核心素养的具体体现. 本文只是较为粗浅的基于课堂教学点的实施谈及数学核心素养的培养.总之,如何在数学活动中培养学生的核心素养,已经成为我们每一位数学老师义不容辞的光荣使命.让我们积极转变教学理念,改进教学,积极实践吧!

