基于Matlab的神经网络在绵阳空气质量预测中的应用
陶雪梅,李 高
(绵阳市气象局,四川 绵阳 621000)
引 言
绵阳,又称“中国科技城”,位于四川盆地西北部,涪江中上游地带。冬半年受偏北气流控制,气候干冷少雨;夏半年受偏南气流控制,气候炎热、多雨、潮湿。随着城市发展规模不断扩大及城市人口的不断增加,城市问题日益突出,污染物排放量随之增加,空气污染严重,直接危及人类健康。
空气质量指数(AQI) 动态变化平均态可反映出总体的变化趋势[1],但通常使某些极端污染事件被平滑掉。为了细致了解绵阳空气质量的状况,分析了2014 年至2019年AQI月变化趋势如图1。AQI 冬季高,春季居中,夏秋低。由于冬天空气流动性比较差,而且空气中的污染物增多[2]。除了原有的装修、家具、电脑产生的有害气体甲醛、氨气、苯和放射性物质和电子污染以外,天气冷不可能会经常开窗通风,空调取暖,室内的一氧化碳、二氧化碳和漂浮的灰尘、颗粒物都会逐步增多。直接导致冬季空气质量最差。
空气质量主要以SO2、NO2、PM10三种污染物浓度来衡量。污染物浓度除了受排放量的变化影响之外,另一主要影响因素就是气象要素的变化。因此对绵阳市的空气质量进行分析,研究影响绵阳市环境空气质量的关键气象因子[3],并寻找一种适合的分析方法,对有效防控大气污染提供科学依据,对空气质量预测预报模型的建立提供技术指导。
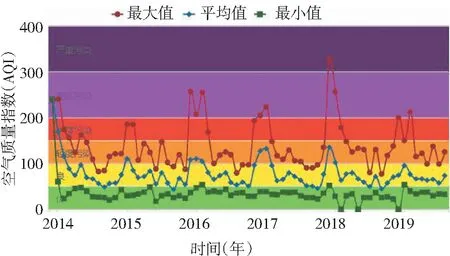
最小值43,平均值77,最大值240图1 绵阳空气质量指数月变化趋势Fig.1 Monthly variation trend of air quality index in Mianyang
1 资料的选取
空气污染历史资料选取2014~2016年的AQI、PM2.5、PM10、SO2、CO、NO2、O3-h08(臭氧含量的8小时滑动平均值);空气污染物浓度为8小时滑动平均值;由于部分气象要素对于空气污染的影响具有滞后性,地面气象实测资料选取前日平均气压、前日平均温度、前日相对湿度、当日风速、当日最大风速、当日降水量8~20(当日08~20点累计降水量)、当日日照时数等7种对污染影响较大的气象要素。
2 多元线性回归预测方法
采用Matlab中的多元线性回归方法[4],分析哪些是主要影响因素,并建立回归模型,验证该模型拟合程度。
2.1 建立回归模型
使用多元线性模型 y=b1+b2x1+b3x2+b4x3+b5x4+b6x5+b7x6+b8x7;输入x1至x7,分别为2014~2016年每日的前日平均气压、前日平均温度、前日相对湿度、当日风速、当日最大风速、当日08~20点累计降水量、当日日照时数等7种对污染影响较大的气象要素;输出y,为2014~2016年每日的空气质量等级。
在matlab中进行多元线性拟合,可以得到以下结果,其中回归系数b如图2、回归系数的区间估计bint如图3、验证拟合显著性各参数如图4。
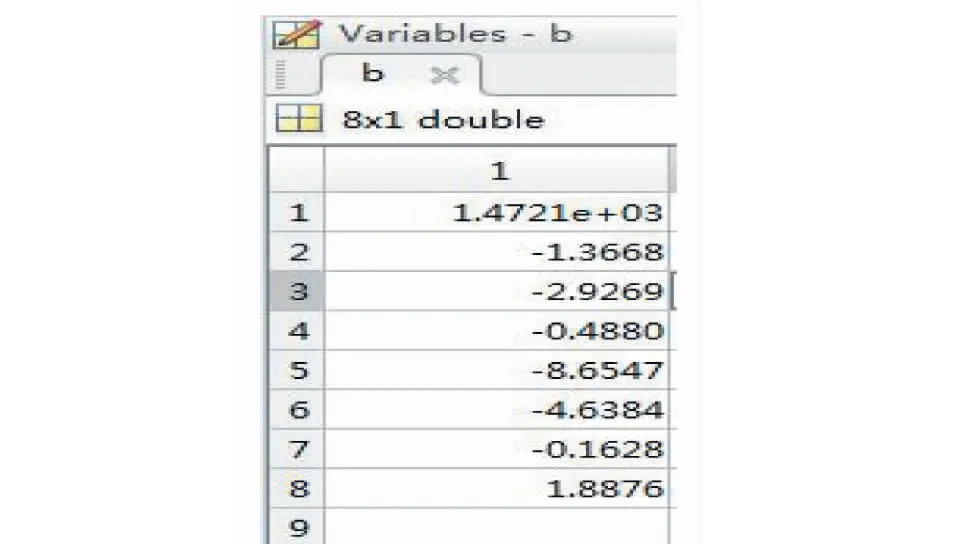
图2 系数bFig.2 Coefficient b
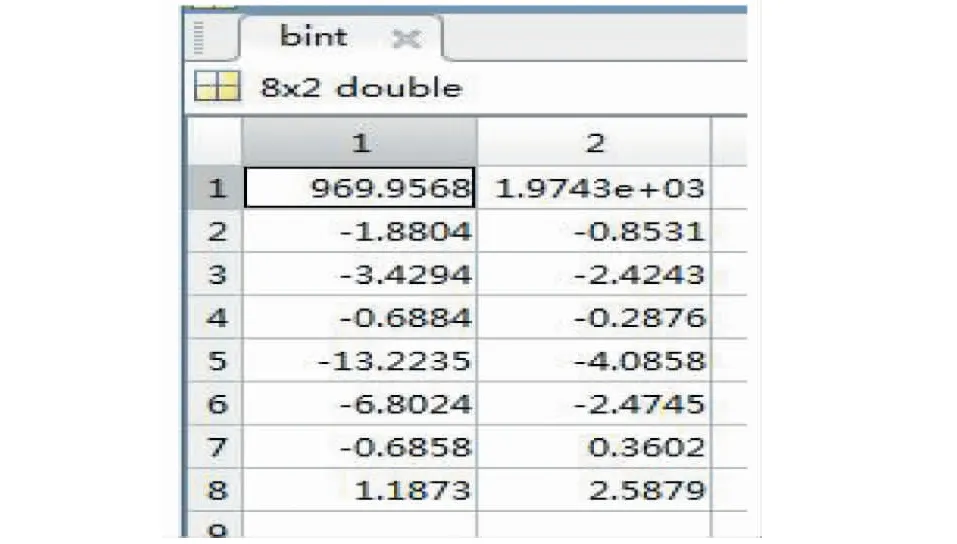
图3 b的置信区间Fig.3 Confidence interval of b
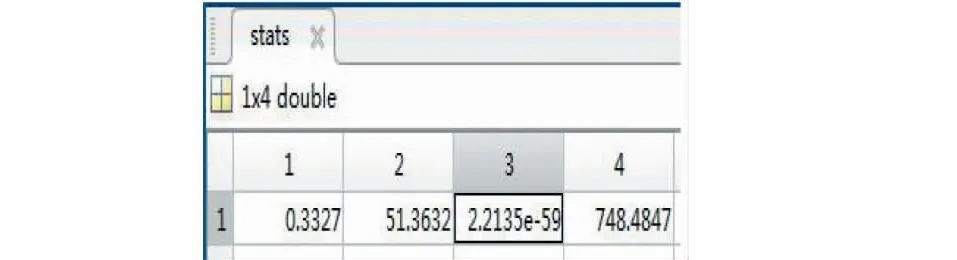
图4 拟合显著性的值Fig.4 Fit significance value
2.2 模型拟合
对模型拟合效果的阐述r2=0.3327,对回归模型整体的方差检验F=51.3632,判断F检验是否显著p=2.2135e-59。由r2=0.3327可以看出,通过该方法拟合出的结果,自变量对于因变量的解释率仅为33.27%,显然远远达不到要求,因此采用回归方程,仅用气象要素因子对空气污染的预报模型误差较大,认为不成立。
3 神经网络的预测方法
采用MATLAB中的神经网络工具箱函数编制
网络建立、训练、测试的程序。通过不断试算[5],分析不同结构参数或以不同算法训练的网络模型的性能,选择合理的网络结构及训练方法,探寻提高网络泛化能力和预报精度的方法。
针对本文研究的模型,采用含有一个隐含层的三层BP网络。
(1)输入输出节点的选取
输入层接收外部的输入数据,其配置必须考虑那些可能影响到输出的参数。但输入的纬数过多会使网络的计算量激增,从而导致系统收敛慢,甚至瘫痪。对于本系统,空气污染的形成不外乎两个途径:污染源(即SO2、CO、NO2、O3-h08等)的直接影响及气象条件对污染物的扩散、稀释和累积。因此输入节点选取除了地面气象实测资料的前日平均气压、前日平均温度、前日相对湿度、当日风速、当日最大风速、当日降水量8~20、当日日照时数等7种影响较大的气象因子外,还选取前日的空气污染指数AQI、PM10、SQ2、CO、NO2、O3等6种因子,共13种输入因子作为输入节点数据。输出层节点数为1(即当日空气的质量等级)。
(2)隐含节点的选取
隐含节点数的选取原则一般是在能正确反映输入输出关系的基础上,尽量选取较少隐含节点个数。然后在训练中根据情况逐步增加,直到满足网络性能要求为止。
隐层节点数的初始值可以参照以下公式来确定:
其中:n为隐层节点数,ni为输入节点数,no为输出节点数,a为1~10之间的常数。
本文根据输入、输出节点数及尽量小的a值,初始选取隐含节点为5~15,针对不同隐含层对网络进行训练,分析预测效果如图5,最终选择最佳隐层节点数5。
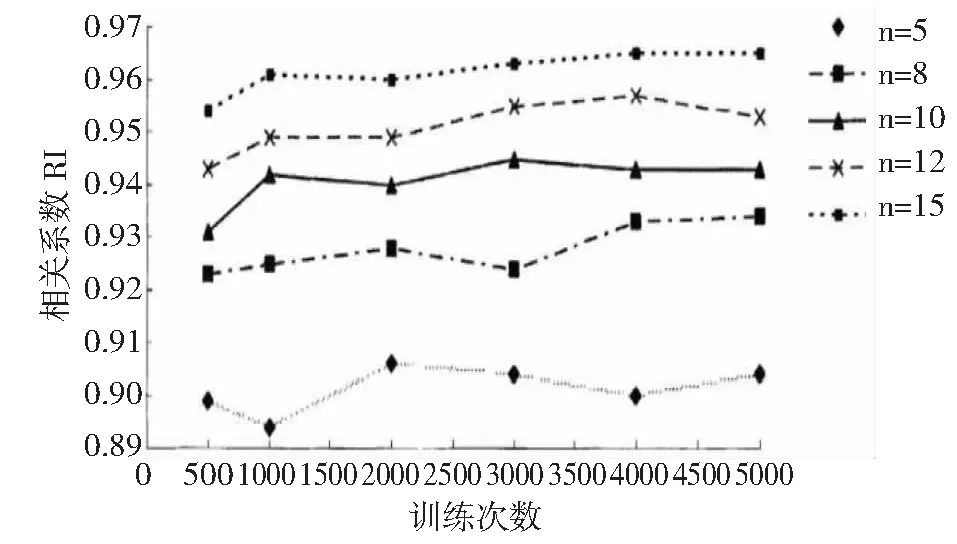
图5 隐层节点数及训练次数对训练样本相关度的影响Fig.5 The influence of the number of hidden layer nodes andtraining times on the correlation of training samples
(3)训练方法的选取
改进的BP算法主要分为两大类:一类是对误差性能函数梯度加以分析从而改进的启发式学习算法,如动量BP算法、学习率可变的BP算法等;一类是基于数值最优化理论的训练算法,如拟牛顿法、L-M算法、共轭梯度法、SCG算法等。选取不同算法在相同条件下,对网络进行训练,结果比较分析,选用均方误差作为算法选择的标准,如下表。
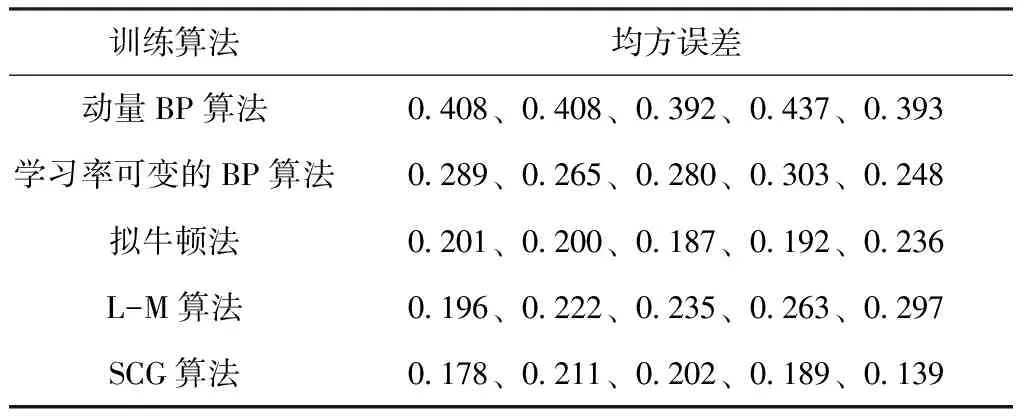
表 不同BP算法训练效果对比Tab. Comparison of training effects of different BP algorithms
采用newff()函数建立网络对象,由于newff()调用的初始化权值的随机性,所以每次训练结果不同,表中列出的是五次随机运行的结果。可以看出SCG算法的均方误差相对比较小,且稳定。因此选择SCG算法作为本模型的训练方法。
为了提高网络的泛化性能,采用在SCG算法中使用提前终止法(训练函数为trainscg),trainscg也叫比例共轭梯度法,将模值信赖域算法与共轭梯度算法结合起来,减少用于调整方向时搜索网络的时间。该训练方法是一种快速训练函数,是权值训练方法对网络进行训练,在训练中求得最佳训练时间时停止训练,避免出现过度拟合。使用该方法训练时,函数会将初始输入数据分为3个子集:训练集、验证集和测试集。在训练过程中网络会使用训练集训练出的网络模式,用验证集来进行验证,如果验证误差增大到一定程度,网络训练提前终止。这时训练函数会返回验证误差最小值时的网络对象。
输入数据选取2014~2015两年的数据(共729个)作为样本。因提前终止法需要构造确认样本集,因此将数据采用等间隔的方式抽取分为三部分,其中1/4用于验证,1/4用于测试,剩余1/2用于训练网络。
3.1 数据初始化处理
(1) 首先建立输入向量矩阵p与输出向量矩阵t,大小分别为13*729,1*729。
(2) 对数据进行归一化处理,采用prestd()函数对输入p,输出t进行归一化处理,以保证数据集具有零均值。得到归一化矩阵pn、tn如图6、图7。
[pn, meanp, stdp,tn,meant,stdt]=prestd (p,t);
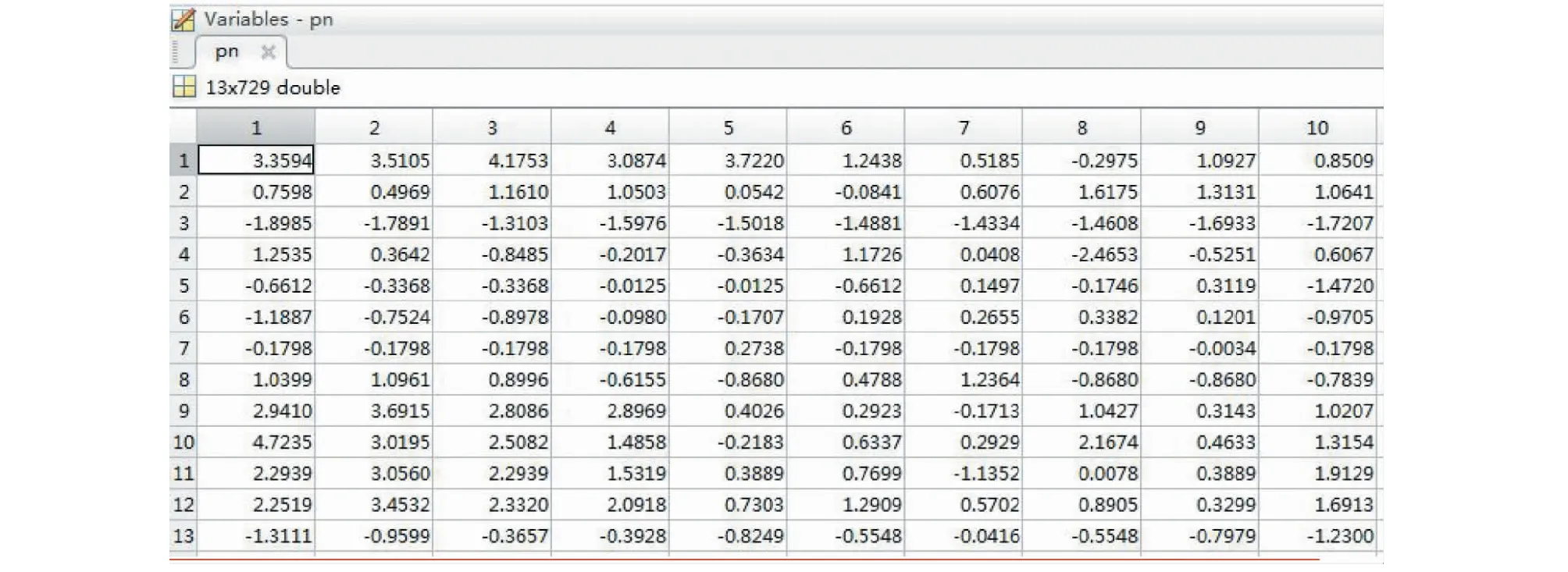
图6 归一化处理后的输入矩阵pnFig.6 Normalized input matrix pn

图7 归一化处理后的输出矩阵tnFig.7 Normalized output matrix tn
(3)对输入向量进行主成分分析,采用prepca()函数进行主成分分析。只保留所占99%的主要成分数据。
[ptrans,transMat〗=prepca (pn,0.01);
其中ptrans数组是主成份分析以后得到的矩阵,下面对分析后的矩阵进行检验,
[R,Q]=size(ptrans)
R=8, Q =682
可以看出ptrans是一个8列682行的矩阵
可以看出看出通过主成分分析,输入向量的纬数从13降到了8,向量维数降低了。降低了原输入数据的冗余度。
(4)构造训练样本集、验证样本集与测试样本集。
val为验证样本,.P为输入,.T为输出,test是测试样本。各种样本的选择采取从中间间隔选取数据,以达到样本的代表性及合理。
iitst=2:4:q;
构建iitst矩阵,从2开始,步长为4,直到小于q=729,为后面间隔选取测试样本集提供参数,如下式(2)。
iival=4:4:q;
构建iival矩阵,从4开始,步长为4,直到小于729,为后面选取验证样本集提供参数,如下式(1)。
iitr=[1:4:q 3:4:q];
构建iitr矩阵,由1开始,步长为4,直到小于729和由3开始,步长为4,直到小于729两个组成,为后面选取二分之一为训练样本提供参数,如下式(3)。
val.P=ptrans(:,iival);val.T=tn(:,iival);
(1)
式(1)表示按照iival数组的列数提取ptrans矩阵中的值,构建验证样本集。
test.P=ptrans(:,iitst);test.T=tn(:,iitst);
(2)
式(2)表示按照iitst数组的列数提取ptrans矩阵中的值,构建测试本集。
ptr=ptrans(:,iitr);ttr=tn(:,iitr);
(3)
式(3)表示按照iitr数组的列数提取ptrans矩阵中的值,构建训练样本集。
3.2 训练模型建立
定义网络和训练网络,得到训练模型如图8。
net=newff(minmax(ptr),[5,1],{′tansig′,′purelin′},′trainscg′);
newff为网络的生成,隐含层神经元个数5,输出层个数1,传递函数tansig为正切S型传递函数,输出层传递函数选为线性函数purelin,训练函数为trainscg。
net.trainParam.epochs=100;
其中epochs用来定义训练迭代的最大值
[net,tr]=train(net,ptr,ttr,[],[],val,test);
采用train函数对生成的网络进行训练。
从结果弹窗中可以看出,经过43次迭代,完成了神经网络的运算,并通过了6次有效性测试。
3.3 模型验证
将训练误差、验证误差和测试误差绘制在一幅图中,以直观地观察训练过程,如图9。从提前终止法的训练过程可以看出,测试误差和验证误差性质变化趋势相同,表明样本集的划分是合理的。
最后,利用训练好的网络对测试样本进行预报,结果如图10所示。
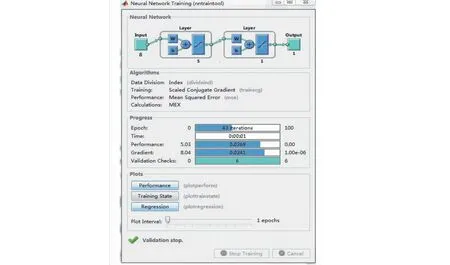
图8 BP网络污染预测模型结构Fig.8 BP network pollution prediction model structure
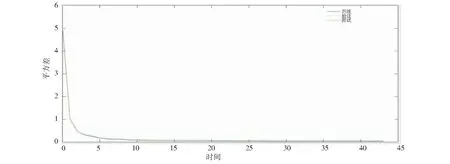
图9 训练误差、验证误差和测试误差对比Fig.9 Comparison of training error、verification error and test error
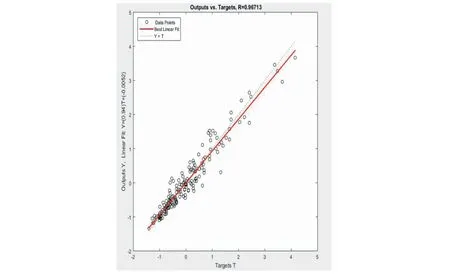
图10 预报值与实际值间的线性回归结果Fig.10 The result of linear regression between forecast value and actual value
rn=sim(net,test.P);
[M,B,R]=postreg(rn,test.T);
由此可见预报值与实际值的相关系数达到了0.967 13,预报的精准程度很高。采用该模型预报空气污染是可行的。
4 结 论
4.1 绵阳市一年中冬季出现污染日的几率最大,夏、秋空气质量比较良好。
4.2 采用多元线性回归分析方法建立的预报模型对原始数据的拟合及预测存在较大误差,自变量对于因变量的解释率仅为33.27%;基于BP神经网络,采用训练方法为SCG 算法的提前终止法对网络进行训练,并利用测试样本集对预报模型的仿真结果进行检验,预报值与实际值的相关系数达到0.967 13。
4.3 用神经网络技术进行空气质量的预测是一项涉及面很广,还有很大深度进行研究的工程,本文只是初步探讨了两种预测模型。对于特殊条件如周末、城市不同的功能区、更多的气象因子的影响、污染源、污染物等对空气质量影响还无法深入研究。对于绵阳市的空气污染的防治还需强化对各区域“散乱污”企业、砖瓦企业、建筑工地、道路扬尘等污染问题进行专项整治,确保我市环境空气质量持续改善。

