基于Benford定律的会计师事务所业务承接研究

刘薇 许池东

1935年美国教授Frank Benford发现了Benford定律，即自然发生的数据，只要样本足够，数据1到9作为首位数字的概率单调递减，之后发表了相关研究成果。后来学者们探讨了Benford定律在会计与审计领域的应用。应用Benford定律是否可以帮助会计师事务所进行审计质量控制，尤其是优化业务承接决策，以此来降低审计风险？就此问题，本文将结合H事务所的案例作出研究。

一、Benford定律理论基础与相关研究

（一）Benford定律的来源

1851年美国数学家Simon Newcomb发现其使用的对数表的首页比后续页面的磨损更加严重。他发现其他现象中的许多类型的数据也有这种奇怪的现象：数字1和数字2相比，数字1作为首位随机数的频率更大；数字2和数字3相比，数字2作为首位随机数的频率更大；数字3和数字4相比，数字3作为首位随机数的频率更大，剩余情况依次类推。

1935年，同样是在使用对数表的美国教授Frank Benford也察觉到了这种奇怪的现象。他发现，图书馆很多辞典的前几页比后来的页面更脏，磨损更多。Benford教授仔细研究后得出结论：只要数据样本足够，数据1到9作为首位数字的概率单调递减。Benford发现了许多不同的数据，如人口、会计、股票市场、化学和物理常数、宏观经济数据、篮球比赛的数量、河流的长度、每个城市的人口分布数据，以及一些杂志中的所有数据等的首位数字出现特点，均与之前发现的规律有一定的相似。最后得出了描述概括规则的数学表达式，被称为Benford定律，也被称为数字的第一定律。

（二）Benford定律的内涵

Benford定律描述的是自然数1到9在自然状态下作为首位数出现的频率，公式为：

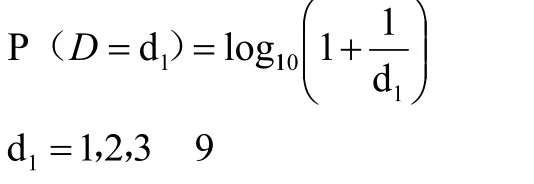
其中P表示d1作为首位数字出现的概率。随着首位（第一位非0）数字的增大，首位数字的随机比率会逐渐减小，以9为首位数字（最大)出现的随机概率最小，其分布概率如表1、图1所示。

从表1和图1可以明确看出Benford定律的概率分布和基本原则，数字1到数字9作为首位数的频率是单调递减的，且程度越来越小。

（三）Benford定律的适用范围

虽然Benford定律从一开始就被用于各个领域的统计数据质量测试，但它与其他数据质量评估方法一样，需要限定使用范围和场合。外国学者Nigrini（1992）分析并验证了Benford定律，指出根据福特法律使用的数据集必须满足四个主要要素：

1.数据必须数量足够才能具有整体数据的重要特征；

2.数据不应有人为限制，并且没有指定的最大值和最小值；

3.数据的形成应受多种因素的影响，但人为因素的影响应相对较小，不能发生人工估价现象；

4.数据无法按规律排序。

（四）Benford定律会计审计领域应用的相关文献综述

1.国外研究

Carslaw（1988）最早运用Benford定律评估会计领域的数据，他从上市公司年报中提取总收入这一科目，发现该数据集的第二位数字出现0的概率，在统计学意义上显著大于出现数字9的概率。他分析这一现象可能是由于管理者有意识地提高收入数据造成的，例如将1999记为2000。由此发现新西兰上市公司管理层实施了积极的盈余管理。Nigrini(1997)将Benford定律广泛应用到财务审计领域，认为在检查会计账目是否造假和纳税申报中企业是否人为操纵财务数据时，可以使用Benford定律加以分析验证。这是西方学者首次使用Benford定律检查审计领域中的财务舞弊行为，在此之后，他又将领域扩大到会计和金融，最后更延伸至选举中的数据造假现象。Nigrini还开发了运用Benford定律对财务数据进行测试的软件，之后，许多软件都加入了这一功能，国际上的著名审计软件ACL和IDEA等也将Benford定律作为内置功能。此后在美国，该定律在部分实用领域进行了实践。在经济方面，会计师可以根据这一定律对公司的年度账目进行分析，查找伪造数据。例如，美国安然公司会计舞弊案披露后，人们发现该公司在2001-2002年所公布的每股盈利数字不符合Benford定律，这证明了安然的高层领导确实改动过这些数据。在宏观经济统计领域，Benford定律己被用于评估国内生产总值(GDP)、居民消费价格指数(CPI)和广义货币供应量(M2)等宏观数据的准确性。在选举方面，Benford定律也用于投票欺诈发现，科学家在2004年美国总统大选中发现了佛罗里达州的欺诈行为，以及2004年委内瑞拉和2006年墨西哥的投票欺诈行为。

2.国内研究

冯郁，丁国勇（2003）对某高校财务数据的首位数字分布及前两位数字分布分别运用Benford定律进行分析，发现前两位数字的分布呈现出“整点效应”现象。张苏彤（2005）对我国1394家上市公司财务数据进行Benford定律的验证性测试，同时采用“模拟造假”方式形成了虚假数字进行结果对比，发现上市公司数据与Benford分布更为接近。同时提出，对于大量样本可以进一步分层测试，发现其中的特征。王忍，曹建新（2006）使用Benford定律分析我国A股年报披露的净利润指标时，发现其与Benford理论分布存在较大差异，这种差异不仅存在于亏损企业的数据中，盈利企业也存在人为操纵利润的可能。王福胜，李勋（2007）指出Benford定律的应用属于舞弊侦查方法中的分析性复核法，现有的分析性复核法多是从数据内在逻辑关系出发，而Benford方法是从统计学角度检测数字分布的内在规律，是对传统舞弊侦查方法的很好的补充，给财务舞弊增加了难度。许存兴、王大江、张芙蓉（2009）没有选取正常的审计报告，而是以出现异常的上市公司年报为数据源（即选取被出具非标准意见的年报），利用Benford定律进行检测，发现资产负债表数据准确性较好，而利润表准确性较差；通过比较各季度报表数据准确性，发现第四季度财务数据真实性最高，第二季度财务数据真实性最低。李荟（2012）利用Benford定律研究了上市公司应收账款和主营业务收入的两个科目数据主体，并分析了两个指标首数字的概率分布，结果发现，这两种分布都遵循Benford定律，但应收账款与Benford定律符合程度较高，主要业务收入则较低。因此她认为，相比操纵资金往来项目（应收账款），上市公司更倾向于操纵利润指标（主营业务收入）进行欺诈。

图1 Benford定律数字概率分布图

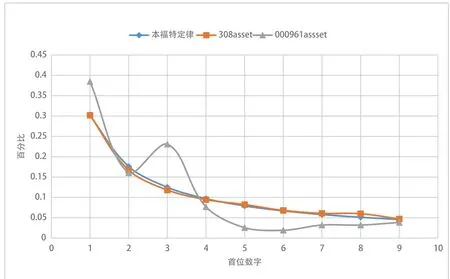
图2 资产负债表指标首位数字频率分布对比图例

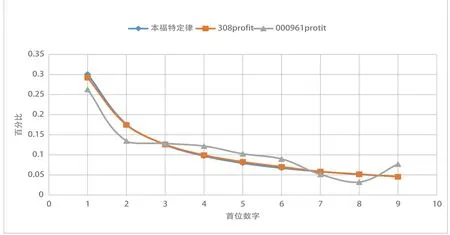
图3 利润表指标首位数字分布频率对比图例

二、会计师事务所业务承接理论分析与文献回顾

对会计师事务所来说，审计风险贯穿于审计业务承接、审计程序执行到审计报告的完成以及报告后的整个过程。对这些风险的控制决定了审计质量控制的水平。只有在审计全流程关注审计风险并将其降低至可接受水平，才能避免审计失败、获得审计收益。审计客户的选择是影响会计师事务所审计风险的重要因素，审计业务承接决策是审计风险控制的第一道防线。如果业务承接不谨慎，没有识别到客户的经营困境或者恶意欺诈，就很容易发生审计失败。而审计失败带来的诉讼风险和声誉损失，对会计师事务所产生的影响也越来越显著。

Chio、Rajib、Doogar(2004)发现会计师事务所承接业务时，会受到当时法律环境的影响，其承接业务的谨慎性与法律风险强弱正相关，即在诉讼风险高峰时期，更不愿意接受高风险的客户。Randal Elder et al（2009）研究发现，事务所为了降低审计风险，出具非标准审计意见报告更多地是针对高风险客户。Esamaddin Khorwatt（2015）认为对客户的内外环境进行分析是承接新业务时必要的审计程序，即识别评估业务承接的审计风险。

谢荣（2003）提出在进行业务承接决策时，必须把握审计风险的可控性和客户的整体情况，除了分析企业的财务状况和经营成果外，还应该详细分析企业的战略目标、商业环境、管理层的经营理念和诚信程度。黄婧媛（2003）通过分析业务承接决策过程中各个风险的确认和相互关系，从风险评估的角度出发，建立了一个接受客户决策的模型。原红旗、李海建（2004）研究发现，在对公司的选择上，不同类型的会计师事务所不存在较大差异，而且被审计公司在财务特征上也不存在较大差异。廖义刚、孙俊奇、陈燕(2009)以客户选择为视角研究提高注册会计师的责任，结果表明，会计师事务所更倾向于选择风险较低的审计客户，以此规避审计风险，维护声誉。徐海玲（2016）研究发现，随着会计师事务所从有限责任制转为特殊普通合伙制，诉讼风险更大，注册会计师的法律风险也增大了，会计师事务所会更加慎重筛选所承接的客户，以此来降低审计风险。

表1 Benford定律数字概率分布表

表2 Pearson相关系数检验标准

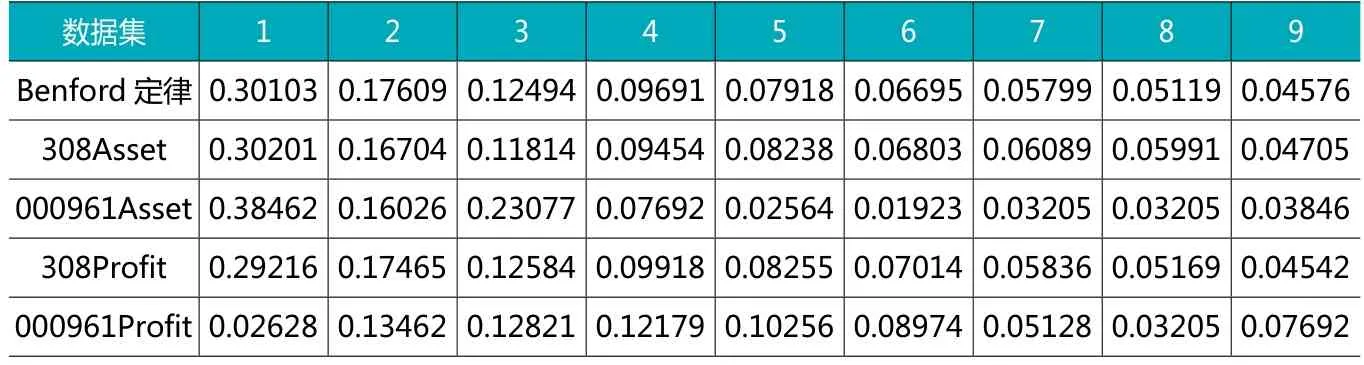
表3 各指标首位数字频率分布对比

表4 各数据集观测频率和Benford定律下频率的Pearson相关系数

从国内外文献回顾看来，现有的关于审计质量控制相关理论起步和实务基础大多是由国外发展而来，国外的学者研究起步早，对于审计质量控制的研究呈现出在具体案例的基础上与多学科结合的趋势，不单单考虑传统的审计业务相关内容，还联系到了企业制度和战略等因素。而国内学者的研究大多是结合我国国内具体的政策背景，综合运用规范研究和案例研究的方法，对于本土出现的审计风险和审计事故进行研究。

综上，已有文献大多研究审计质量控制的目标，在于解决实际工作中可能出现的财务舞弊，财务造假等审计事故，侧重在实务层面上，具体剖析现阶段影响会计师事务所审计质量的原因和对策，而从会计师事务所审计业务承接的角度进行的研究相对匮乏，可以直接检索到的国内外相关文献也比较少，进行实证研究的也极少，大都进行规范性研究。另外，国外和国内学者们对会计师事务所如何优化业务承接决策，降低审计风险，得出的结论也不尽相同，缺乏对具体方法的深入研究，未检索到将Benford定律应用于事务所业务承接研究的相关文献。

三、研究设计

近年来，在我国政策的扶持下，一些内资所己经打破市场垄断，形成国际“四大”、本土“八大”的注册会计师事务所的领军地位。然而与内资事务所排名跃升相反的是，其受到的处罚也接二连三。由于证监会和财政部的监管愈趋严格，会计师事务所在执业过程中可能面临的风险也在逐渐扩大。因此，对于会计师事务所和监管机构来说，如何及时发现其在业务承接和执行审计业务过程中暴露的风险管理缺陷、迅速建立有效的应对机制，成为当前的一大难题。本文将应用Benford定律检验客户的会计数据可靠性的步骤描述如下：

（一）检验步骤设计

1.选择有代表性的数据，采集尽可能多的样本，并对数据进行初步整理；

2.判断使用Benford定律评估该数据集的数据准确性是否适用。由于Benford定律存在一定的适用条件，因此在检测前必须先确认其适用性；

3.对数据进行处理。例如，对含有负值的数据，可以取绝对值；对于为0的数据可以剔除掉等等；

4.提取数据的首位数字，计算其首位数字分布率，与Benford定律进行比较，应用相关系数检验方法进行检验。本文将采取Pearson相关系数的相似度模型进行检验；

5.得出结论。依据给定的显著水平所对应的临界值，判断其是否符合Benford定律。如果符合Benford定律，则说明数据准确性可能较好，如果不符合，则说明数据准确性可能存在问题。

需要说明的是，相似度计算中最常用的方法是基于向量之间相关系数的计算方法，Pearson相关系数是非常适合作为相似度评价标准的一种方法。具体而言，Pearson相关系数利用两个向量之间的线性相关性来定义向量之间的相似度，其输出范围为-1到+1，0代表无相关性，负值为负向，正值为正相关。其统计量公式为：

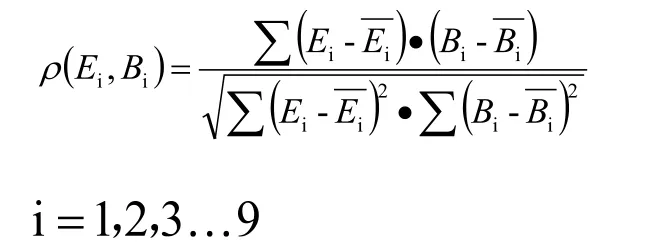
其中， 是数据集的首位数字为i的观测频率， 是Benford定律中首位数字为i的理论频率。分别表示为对应量的均值。的绝对值越接近1，则数据集的首位数字越倾向于服从Benford定律，认为数据准确性越高。 绝对值越接近0，则数据集的首位数字越倾向于不服从Benford定律，认为数据准确性越低。其具体判断标准如表2所示：

从Benford定律的相关概述可以看出，通过对数据的统计和Pearson相关系数检验法的应用，Benford定律是从一种统计分析的角度，来确定数据的准确性。相对于其他各式各样的统计数据质量评估方法，利用Benford定律具有很多特性：1.易操作。即便不是专业人员，也能利用相关软件使用此方法。2.成本低。使用此定律的成本较低，不需要大量的人工与时间，只要数据收集处理符合要求，即可得到对于数据准确性的判断，完全符合大多数单位对于风险评估的预算预期。

（二）数据选择与描述

上市公司数据来源主要有年报、半年报、季报以及特殊事项报告等，其中年报审计最为严格。其中的财务报表包括资产负债表、利润表、现金流量表、所有者权益变动表（或股东权益变动表）以及财务报表附注。

本文选取的数据来自由H会计师事务所出具的2014年度审计报告，且审计意见为标准无保留的316家我国上市公司所公布的2007-2012年年度审计报告中的资产负债表、利润表，数据来源于国泰安CSMAR数据库。选取的数据均经过证监会认可的审计机构审计，针对有调整的报表选取了最终调整后申报的数据，对同时存在合并与非合并报表的，选取了合并报表。

特别要说明的一点是，“ST”制度对于上市公司的影响巨大，是对上市公司的特别处理措施——暂停上市，亦为退市前的过渡阶段。根据中国证监会的有关规定，成为“ST”的原因包括了上市公司出现异常状况，其中包含财务状况异常及其他方面的异常；也包括了上市公司连续亏损。连续亏损的上市公司存在巨大退市压力，也有足够的经济利益驱动上市公司相关方铤而走险，利用各种可能的手段尽可能满足监管要求，其中就包含了财务造假的可能。当然某些马上就会被列为“ST”股票的上市公司存在更高的财务造假可能性，该类公司的数量更多，且很多都存在多次造假记录。综上所述，将H会计师事务所审计的ST企业数据剔除后，本文最终选定309家企业数据（含2017年证监会行政处罚的000961Y实业公司）。

指标选择方面，选择在财务分析中通常使用、投资者关注度高、财务舞弊通常涉及的财务指标，包括从资产负债表指标(Asset)中选取的主要财务项目：应收账款、资产合计、应付账款、负债合计、资本公积、未分配利润、所有者权益；从利润表(Profit)中选取的主要财务项目：营业收入、营业成本、销售费用、管理费用、财务费用、利润总额、净利润。

（三）数据处理

根据上述对Benford定律的描述可以了解到，Benford定律要求第一位数字是有效数字：非负、非零，因此在数据处理时要根据这个原则对所选数据集进行筛选分析。因所选取数据均取自CSMAR数据库，可知数据均符合非负这一原则，因此在运用数据进行实证研究时，本文运用Python3软件对所选取数据集进行去零、去空处理，使得各数据集条件符合Benford定律的基本原则。

通过运用Python3软件及EXCEL软件计算可知，所选取的308家企业2007-2012年度资产负债表（下文简称“308Asset”）包含数据分布为42425，利润表（下文简称为“308Profit”）包含数据分布为40933，被证监会处罚的Y实业公司2007-2012年度资产负债表（下文简称为“000961Asset”）包含数据分布为156，利润表（下文简称为“000961Profit”）包含数据分布为156。

四、实证研究结果

（一）描述统计

根据以上理论和步骤，通过Python3以及Excel软件分析可得出，选取的4个数据集中首位数字出现的频率和Benford定律的期望频率如表3所示。

统计指标Asset的描述性统计如图2所示，可以看出在Asset指标中统计数字集308Asset总的观测频率是呈递减趋势的，数字2、数字3的出现频率出现了轻微的向下浮动，而数字8的出现频率出现了轻微向下浮动，从整体上看基本与Benford定律的曲线吻合，说明308家H所出具标准无保留意见的上市企业的资产负债表数据符合Benford定律特征。数字集000961Asset总的观测频率也呈递减趋势，但可以明显看出数字1的出现频率明显高于Benford定律的期望频率；数字3出现频率有明显向上凸起，高于期望频率；数字5、数字6的频率有较明显的向下凹陷，低于期望频率；数字7、数字8的出现频率轻微向下浮动，略低于期望频率。由于有多个数字的出现频率明显不符合Benford定律特征，说明000961Y实业公司在2007-2012年度的资产负债表存在较大程度的数据篡改可能。

统计指标Profit的描述性统计如图3所示，可以看出在Profit指标中统计数字集308Profit总的观测频率是呈递减趋势的，数字1的出现频率出现了轻微的向下浮动，而数字5、数字6的出现频率出现了轻微向下浮动，从整体上看基本与Benford定律的曲线吻合，说明308家H所出具标准无保留意见的上市企业的利润表数据符合Benford定律特征。数字集000961Profit总的观测频率也是呈递减趋势，可以明显看出数字1、数字2、数字8的出现频率有不同程度的下滑，出现频率有明显的偏低；数字4、数字5、数字6、数字9出现频率有较明显的凸起（上浮），其出现频率高于期望频率。由于有多个数字的出现频率明显不符合Benford定律特征，说明000961Y实业公司2007-2012年度的利润表存在较大程度的数据篡改可能。

综上所述，从表3和图2、图3可以看出，统计数据集308Asset、308Profit中统计数据的第一位数字分布基本都是随着数字的增加，呈不断递减的趋势，且跟Benford定律期望频率相差极小，从观测层面上完全符合Benford定律的基本特征。尽管有部分数字频率与Benford定律下的期望频率不是完全吻合，考虑到CSMAR数据库中数据的取得过程，以及财务报表数据本身就存在一定的调整，有理由相信308家上市企业的2007-2012年度的资产负债表以及利润表的数据质量是比较可靠的，即对H会计师事务所而言，根据以上信息可以表明这308家客户是比较诚信的，会计师事务所承接以上企业2012年度的审计业务的审计风险，在客户诚信层面是比较低的。而统计数据集000961Asset、000961Profit中统计数据的第一位数字分布尽管从整体的角度看是随着数字的增加有不断递减的趋势，同时可以明显看到，有部分数字存在阶段性递增现象，而且个别数字的出现概率和Benford定律下的期望概率有较大差异。对此，我们有理由确定，Y实业公司000961的2007-2012年度的资产负债表以及利润表的数据质量是有待商榷的，存在较大的数据造假可能，即对H会计师事务所而言，根据该信息，可判断承接Y实业公司2012年度的审计业务的审计风险，在客户诚信层面是较高的，这对于审计质量控制方面并不是一个好的信号。

（二）统计检验

Pearson相关系数检验：运用统计软件，求出指标中各数据集内各数字实际出现频率和Benford定律的期望频率的Pearson相关系数。

从表4可以看到计算结果，308Asset、308Prfit两个数据集首数字的分布频率与Benford定律期望的频率分布相差很小，且Pearson相关系数均大于0.99，根据相关系数的评估标准，这两个数据集符合Benford定律，属于高质量数据集。然而000961Asset、000961Profit数据集中，首数字出现频率与Benford定律的期望频率的Pearson相关系数并不理想，相关系数检测可以看出得到的相关系数均小于0.97，根据相关系数的评估标准，此两组数据集存在数据篡改的很大可能，需要进一步检查核实。

综上所述，按照308Asset、308Profit两个数据集代表的实际意义，可以推断出这308家企业2007-2012年度的资产负债表及利润表中财务数据是较为真实可信的，进而推断出对于这308家企业的客户诚信是有保障的，对于H会计师事务所而言，在客户诚信层面的审计风险是较低的。而根据000961Asset、000961Profit两个数据集在Pearson相关系数检验的表现，可以推断出Y实业公司的2007-2012年度的资产负债表以及利润表数据存在较大的数据篡改可能，进而推断出作为会计师事务所客户的Y实业公司高层的客户诚信水平值得商榷，这对于H会计师事务所承接Y实业公司2012年度的审计业务，在客户诚信方面的风险是较高的。而在2017年证监会的行政处罚书中H会计师事务所的审计失败也证明了这一点。

五、主要结论与不足之处

（一）主要结论

1.本文主要针对H会计师事务所2017-2018年间接连被证监会处罚这一现象，从审计业务客户承接这一角度入手，通过结合Benford定律，对CSMAR数据库中的H会计师事务所承接2013年度Y实业公司审计业务以及同期承接审计业务的另外308家非ST企业的资产负债表以及利润表进行研究，得出的结果如下：通过Benford定律对共计309家企业的财务数据进行相关性分析，经过统计检验发现所选数据集中，Y实业公司的数据质量存在问题，在资产负债表中具体表现为数字1、数字3作为首位数的出现频率较Benford定律有大幅度上升，数字5、数字6、数字6作为首位数的出现频率较Benford定律有一定程度的下降；在利润表中具体表现为数字4、数字5、数字6、数字9作为首位数的出现频率较Benford定律有一定程度的上升，数字1、数字2、数字8作为首位数的出现频率较Benford定律有一定程度的下降。而另外的308家企业的数据集无论是资产负债表还是利润表，其各数字作为首位数的出现频率基本与Benford定律相近，数据的质量明显好于Y实业公司的数据。

2.通过本次分析，以及与2017年H所被处罚事件的相互映照，本文认为Benford定律的检验，能够在会计师事务所承接业务前，对客户的诚信有一个比较可靠的预估。对于影响审计质量中的不可控因素——执业的工作环境，有一个了解，对于接下来是否承接或承接业务后注册会计师对于被审计单位数据真实性有一定了解，对开展内部控制测试有一定指导作用。

（二）不足之处

1.不符合Benford定律分布的数据并不一定存在人为篡改，一些正常的业务活动也可能影响数字分布规律，如合理的四舍五入，以及季节性、政策性等外部因素，对此还需要进一步的研究分析。同样，符合Benford定律分布的数据也不意味着其数据准确性完全没有问题，特别是当数据集容量较大的时候，存在准确性问题的数据可能淹没在数据集的规律中而不能被发现。

2.现实中的舞弊手段与舞弊行为更加复杂，其本身可能对数据分布规律不造成影响。对于某些一般不会在账目上反映出来的行为，例如回扣、受贿等舞弊行为等，无法利用Benford定律的相关性检验进行分析。

3.Benford定律并不能直接确定存在异常的某一项具体数据，只能确定是以哪个数字为首位的数据集存在篡改舞弊的可能，具体问题还需要与其他审计方法结合使用才能发现。

（三）下一步研究

通过对客户会计数据进行Benford定律验证，能从总体上把握客户数据的质量水平，有利于会计师事务所做出是否承接审计业务的决策，以降低审计风险，提高审计质量。

如果会计师事务所已经承接了审计业务，可以对客户具体账簿数据进行进一步的Benford定律验证，找到数据异常的具体账户，以确定重点审计领域和重点审计账户。