基于空间回归模型的思茅松林生物量遥感估测及光饱和点确定*

周 律 欧光龙 王俊峰 胥 辉

(西南林业大学 西南地区生物多样性保育国家林业和草原局重点实验室 昆明 650224)

森林生物量估测是当代林业生产和科研的热点问题(王维枫等， 2008)。传统基于地面调查的森林生物量估测需要进行大量实地调查，不仅耗时、耗力，而且还会对实物造成一定破坏(薛巍等， 2009)； 而遥感对地观测技术具有实时、动态、大面积同步监测和信息丰富的特点(梅安新等， 2001)，以电磁信息形式快速记录环境条件、植被分布格局和活动以及土地利用等动态变化，其对植被光合有效辐射吸收的测定为估测植被生物量及动态变化提供了基础(杜华强， 2012)。因此，遥感技术结合少量地面样地调查数据可实现大范围森林生物量时空动态估测，已成为当前森林生物量和碳储量研究的重要技术方法之一(陈庆等， 2014)。

基于遥感技术的生物量估测存在不确定性等问题，其中光饱和点的不确定性尤为突出(于艳梅等， 2012)，即当森林植被密度达到一定阈值时，遥感接收到的电磁辐射信息不再反映生物量的变化，遥感模型对高生物量分布区无法准确估测，从而造成生物量的光饱和点问题(付元元等， 2013)。为了解决该问题，国内外学者进行了大量有益探索，如Zhao等(2016)利用分层理论和半变异函数确定了浙江省6类森林的生物量光饱和点； Kasischke等(1997)基于AIRSAR和SIR-C数据对美国松树林进行遥感估测，得出林分结构复杂的热带森林和单一树种森林光饱和值分别为100 t·hm-2和250 t·hm-2。但是如何进一步确定不同类型森林光学遥感估测的光饱和点、提高森林生物量遥感估测精度、降低森林生物量遥感估测的不确定性仍然是研究的热点和难点。

林业数据具有空间效应，森林植被在生长过程中会受到自身与周围环境相互作用的影响，因此采用传统统计学模型并不符合其对数据独立性的要求(刘茜等， 2015； 张博等， 2016)。空间回归模型广泛应用于公共卫生、疾病预防、区域发展等领域(伍劲屹等， 2013； 黄秋兰等， 2013； 温海珍等， 2011； 付琦等， 2018)，在林业方面也有涉及，如王烁等(2015)构建以最小二乘法为基础的全局模型和以地理加权回归模型为基础的局域模型预估天然红松(Pinuskoraiensis)的分布情况，结果发现地理加权回归模型可有效解决样地间空间异质性问题，有利于提高红松分布的预测精度； 刘畅等(2014)采用普通最小二乘模型、线性混合效应模型和地理加权回归模型分析不同尺度下黑龙江省森林碳储量空间分布，得出地理加权回归模型能够很好解决空间效应问题并可提高拟合精度； 欧光龙等(2014)应用普通最小二乘模型和地理加权回归模型构建思茅松(Pinuskesiyavar.langbianensis)单木树干生物量、树枝生物量、树叶生物量和地上部分生物量，结果表明地理加权回归模型估测森林地上生物量的精度更高，并在一定程度上克服了普通最小二乘模型拟合生物量时存在的异方差问题。但是如何考虑调查样地的空间效应，采用空间回归模型解决森林生物量光学遥感估测中光饱和点带来的高值低估等不确定性问题的研究鲜见报道。

思茅松是云贵高原常见的主要针叶树种之一，以该物种为优势种的森林是我国西部偏干性亚热带的典型代表群系，是南亚热带分布的具有代表性的暖温性针叶林(欧光龙等， 2015)。本研究以云南省普洱市思茅松林为研究对象，基于Landsat8 OLI遥感影像数据和森林资源二类调查数据，确定思茅松林生物量光学遥感估测的光饱和点，构建空间全局和局域遥感信息模型反演思茅松林生物量，以期为思茅松林生物量遥感估测提供参考。

1 研究区概况

普洱市位于云南省西南部，地理位置介于22°02′—24°50′N、99°09′—102°19′E之间，东临红河、玉溪，南接西双版纳，西北连临沧，北靠大理、楚雄，东南与越南、老挝接壤，西南与缅甸毗邻，境内群山起伏，全区山地面积占98.3%。北回归线横穿普洱市中部，受地形、海拔影响，垂直气候特点明显。普洱市海拔317～3 370 m，中心城区海拔1 302 m，年均气温15～20.3 ℃，森林覆盖率超过67%。思茅松是普洱市主要用材树种和造林树种，面积达138万km2。

2 研究方法

2.1 数据收集与处理

2.1.1 遥感数据收集与处理 遥感数据为2016年3月Landsat8卫星遥感影像数据，从地理空间数据云网站下载得到。根据研究区行政区划分布，覆盖研究区的Landsat8影像数据7景，条带号分别为129/044、129/045、130/043、130/044、131/043、131/044和131/045。对遥感影像数据进行影像地理配准、地形校正、辐射定标等处理后，裁剪拼接得到研究区卫星影像，如图1所示。

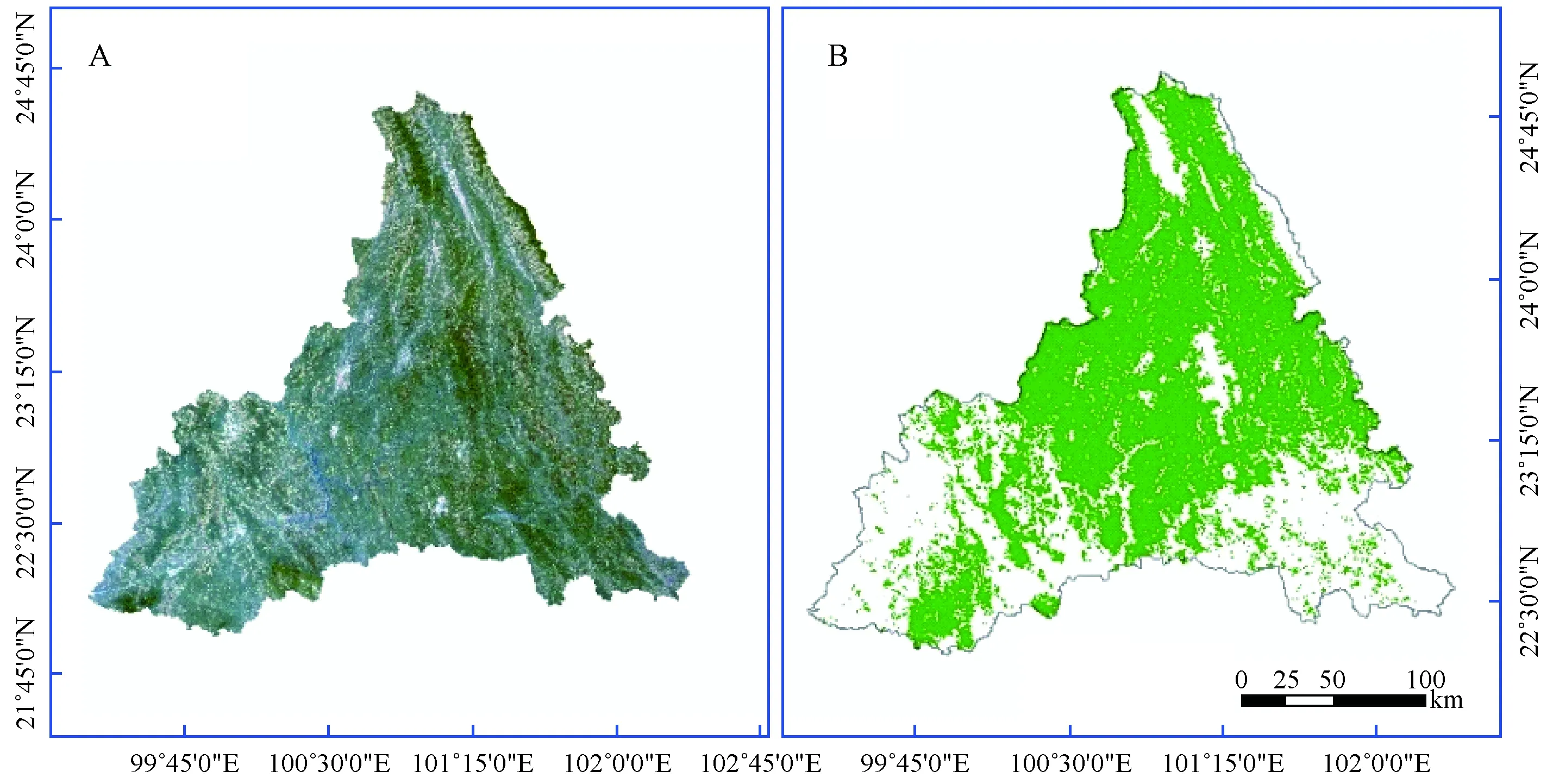
图1 研究区卫星影像Fig.1 Satellite images of study areaA.普洱市Landsat 8 OLI(4/3/2)波段合成遥感影像Landsat 8 OLI images of Pu’er city synthesized by 4/3/2 band； B.普洱市思茅松林分布Simao pine forest distribution of Pu’er city.

为了建立思茅松林生物量遥感估测空间模型，基于Landsat8 OLI遥感影像，选择单波段(B1、B2、B3、B4、B5、B6、B7)以及主成分变换(PCA)、缨帽变换(KT)和植被指数[差值植被指数(DVI)、垂直植被指数(PVI)、土壤调节植被指数(SAVI)、归一化植被指数(NDVI)、大气阻抗植被指数(ARVI)等]等共31个遥感变量，如表1所示。

2.1.2 样地数据收集与生物量计算 样地数据为2016年普洱市森林资源二类调查小班数据，因数据量较大，剔除异常小班数据，最后筛选得到700块小班进行分析。采用朱丽梅等(2009)构建的思茅松单木树干、树枝和树叶生物量估算模型，基于林分平均胸径计算小班生物量，以此作为小班林木的平均单木实测生物量：

W=WS+WB+WL=0.026 5D2.609 8+
0.002 1D3.3718+0.040 6D3.230 7。

(1)

式中：W为思茅松单木地上生物量(t·hm-2)；WS为思茅松单木树干生物量(kg)；WB为思茅松单木树枝生物量(kg)；WL为思茅松单木树叶生物量(kg)；D为树木胸径(cm)。

通过小班单位面积林木株数计算得到小班单位面积地上生物量。

对思茅松生物量样本数据，随机抽取约70%样本(500个)用于建模，剩下约30%样本(200个)用于模型验证。

2.2 生物量与遥感变量的相关性分析

利用ArcGIS软件提取每个小班遥感变量，采用SPSS软件选择皮尔逊相关系数分析生物量与各遥感变量的相关性； 选择与生物量相关性显著的遥感变量进行逐步线性回归，以方差膨胀因子(VIF)小于10为标准进行变量共线性诊断，决定系数最高的模型用于后续光饱和点确定及建模采用变量。

2.3 生物量遥感估测的光饱和点值确定

采用二项式函数、幂函数2种方法拟合生物量与波段反射率之间的函数关系，通过计算函数所对应的拐点值确定生物量遥感估测的光饱和点值。

2.4 模型构建

2.4.1 普通最小二乘模型 普通最小二乘模型(ordinary least squares，OLS)自变量X与因变量Y的关系可通过最小二乘方法表示：

Y=Xβ+ε。

(2)

式中：β为模型参数；ε为模型残差，且服从N(0，σ2)分布。

参数β采用因变量与预测值之间的离差平方和最小的方法来估计，可表示为矩阵形式：

(3)

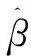
OLS是一个全局模型，模型中常数和解释变量的系数在不同研究区域间是相同的，不能体现各区域间的空间差异性。

表1 遥感变量①Tab.1 Remote sensing variables used in the study

①NDVI为归一化植被指数，SRI为比值植被指数，SAVI为土壤调节植被指数，PVI为垂直植被指数，BVI为亮度植被指数，GVI为绿度植被指数，WVI为湿度植被指数，IIVI为红外植被指数，DVI为差值植被指数，ARVI为大气阻抗植被指数，TVI为转换型植被指数，MVI5为短红外植被指数，MVI7为中红外植被指数，Albedo为反照率； PCA1～PCA7为主成分变换，KT1、KT2、KT3为KT变换； 下同。NDVI is normalized difference vegetation index, SRI is simple ratio index, SAVI is soil adjusted vegetation index, PVI is plumb vegetation index, BVI is brightness vegetation index, GVI is greenness vegetation index, WVI is wetness vegetation index, IIVI is infrared index vegetation index, DVI is difference vegetation index, ARVI is atmospheric resistant vegetation index, TVI is transformed vegetation index, MVI5 is moisture vegetation index using Landsat’s band 5,MVI7 is moisture vegetation index using Landsat’s band 7,PCA is principal component analysis, KT is tasseled cap transformation. The same below.

2.4.2 空间滞后模型 空间滞后模型(spatial lag model，SLM)也称空间自回归模型。当解释变量存在显著空间依赖性，仅仅考虑其自身解释变量不足以很好估计和预测该变量的变化趋势时，可将空间滞后项作为新的解释变量引入到经典统计回归模型中，再通过计算空间相关系数衡量空间相关的方向和大小。可见，SLM模型是通过在OLS模型中加入因变量y的空间滞后项来实现的：

Y=Xβ+ρWy+ε。

(4)

式中：Y为因变量；X为自变量；β为预估参数；W为行标准化的空间权重矩阵；Wy为临近样地点y的加权平均值(即空间滞后项)，可以评价空间自相关程度；ρ为空间自相关参数，受W矩阵影响；ε为服从N(0，σ2I)正态分布的随机误差项。

2.4.3 空间误差模型 当模型误差项在空间上相关时，即为空间误差模型(spatial error model，SEM)。SEM模型假设因变量之间不会直接产生影响，空间自相关来源于误差，即将最小二乘法的模型误差分为2部分，空间自相关带来的误差项和模型自身误差：

Y=Xβ+λWε+ξ。

(5)

式中：Y为因变量；X为自变量；β为预估参数；W为行标准化的空间权重矩阵；λ为空间自相关参数；Wε为空间误差项；ξ为服从N(0，σ2I)正态分布的随机误差项。

2.4.4 地理加权回归模型 地理加权回归模型(geographically weighted regression，GWR)寻找空间的局部变异，并通过在数据上移动的一个加权窗口在每个选择点估计一组系数值。如果局部系数值在空间内变化，则表明其在此位置不稳定。GWR模型的基本形式如下：

y(ui,vi)=β0(ui,vi)+β1(ui,vi)x1i+

β2(ui,vi)x2i+…+βn(ui,vi)xni+εi。

(6)

式中： (ui,vi)为i点处坐标；y(ui ,vi)为i点处的因变量；n为样本个数；xni为第n个变量在i点的值；β0为截距；βn为第n个变量的回归参数；εi为服从N(0，σ2I)正态分布的随机误差项。

2.5 模型评价与检验

采用决定系数(R2)和信息准则(AIC)评价4种模型(OLS、SLM、SEM和GWR)的拟合精度。选取总体相对误差(RS)、平均相对误差(EE)和总体相对误差绝对值(RMA)对模型的独立性进行检验(陶长琪等， 2014； 闾妍宇等， 2017)。

采用刀切法分组，将生物量进行分段处理，即0～50 t·hm-2、50～100 t·hm-2和大于100 t·hm-2，选取平均残差(ME)和平均相对残差(MRE)评价各模型在不同生物量大小等级的预估能力：

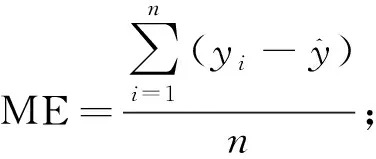
(7)

(8)

2.6 生物量反演

基于所构建的OLS、SLM、SEM和GWR模型，反演普洱市思茅松林生物量。

3 结果与分析

3.1 相关性分析

由表2可知，除了DVI外，其他遥感变量在0.01水平均与生物量具有显著相关关系。为避免变量之间的共线性问题，采用逐步线性回归最终筛选出B1、SAVI和PCA2等3个变量作为思茅松林生物量估算的遥感变量。

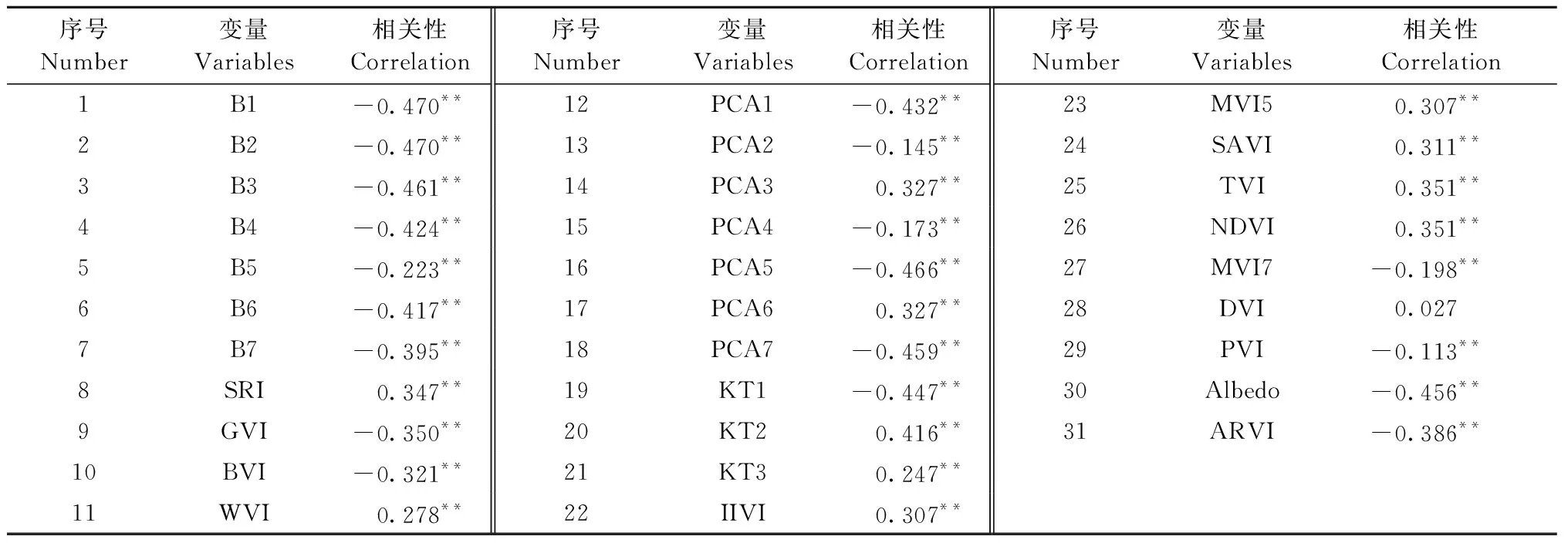
表2 遥感变量的相关性分析①Tab.2 Correlation analysis on remote sensing variables

①**表示在0.01水平显著。** indicates a significant level of 0.01.

3.2 光饱和点值确定

基于选择的B1、SAVI和PCA2这3个遥感变量，采用二项式函数和幂函数求解思茅松林地上生物量与对应波段间的函数关系，函数在区间内的极值所对应的自变量即为思茅松林地上生物量估测的光饱和点。由表3可知，采用B1变量进行二项式函数拟合时具有最高的R2(0.284)，故以其对应拐点作为普洱市思茅松林生物量的光饱和点，其值为106.3 t·hm-2(图2)。

表3 思茅松林光饱和点估计结果Tab.3 Light saturation point estimation of Simao pine forest

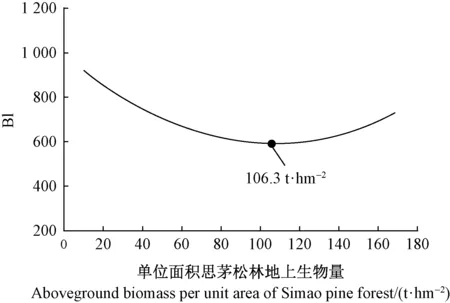
图2 二次项函数拟合思茅松林生物量光饱和曲线Fig.2 Biomass light saturation curve of Simao pine forest using quadratic function

3.3 模型拟合与评价

3.3.1 带宽确定 为在同一尺度下比较空间全局和局域模型，本研究通过ArcGIS软件空间统计分析模块中的增量自相关来确定最佳距离带宽。在计算过程中，保证每个观测点至少存在1个临近点，采用ArcGIS进行临近点距离分析，得出最大邻近距离为34 312.046 m。进行增量空间自相关分析时，起始带宽距离设为34 400 m。当带宽距离为34 600 m时，Moran’sI为0.159 8，相对应的Z值为14.825 7，并通过了显著性检验，说明该带宽距离下思茅松林生物量呈极显著正相关。而且，此距离时Moran’sI显著且Z值到达第一峰值，因此将带宽设为34 600 m，并作为思茅松林生物量空间回归模型构建的最优带宽距离。

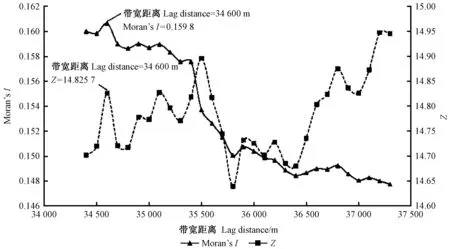
图3 思茅松林生物量Moran’s I指数和Z值的变化Fig.3 Changes of Moran’s I index and Z value of biomass with the lag distance for Simao pine forest

3.3.2 模型拟合 借助GeoDa和GWR4.0软件，选择训练样本(500个)分别对OLS、SLM、SEM和GWR模型进行拟合。由表4可知，模型残差的Moran’sI指数不独立，即存在空间自相关性，不符合最小二乘模型的残差独立性要求，因此在构建思茅松林地上生物量遥感模型时，需要考虑以空间自相关为前提的空间回归模型，从而定量探讨遥感因子与思茅松林地上生物量间的关系。选择带宽距离34 600 m，构建SLM、SEM和GWR模型，SLM、SEM和GWR模型残差的Moran’sI指数检验不显著，说明其空间自相关不显著，在一定程度上解决了OLS模型拟合时存在的空间自相关问题； 此外，SLM模型的稳健拉格朗日乘数不显著，且SEM模型较OLS和SLM模型的AIC小，R2增大，说明SEM模型可较好拟合数据的全局性结构。根据Fotheringham(2004)的评价标准，只要GWR模型与OLS模型的AIC之差大于3，即使将GWR 模型的复杂性考虑在内，GWR模型也比OLS模型执行得更好。本研究AIC从OLS模型的4 628.7下降到4 577.8，差值大于3，R2达到0.373，说明GWR模型的解释能力优于OLS模型，即GWR模型拟合精度显著优于OLS模型，也优于其他全局空间回归模型。

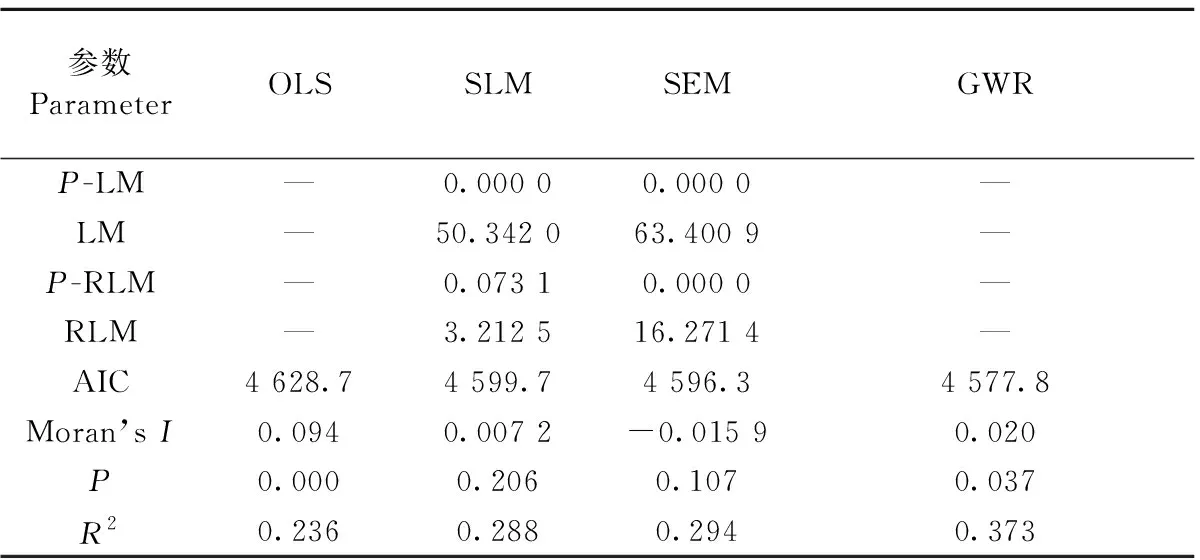
表4 OLS、SLM、SEM和GWR模型比较Tab.4 Model comparison among OLS, SLM and SEM

此外，从GWR模型的方差分析结果可知，相比OLS模型，GWR模型有所改善，平方和残差降低54 459.958，均方残差降低1 689.435，表明OLS模型残差存在显著空间自相关和空间异质性，而GWR模型很好解释了模型残差存在的空间效应问题，使模型精度得以提高(表5)。

表5 GWR模型方差分析Tab.5 Variance analysis of GWR model

根据置信区间检验方法对比分析GWR和OLS模型自变量回归参数平稳性发现，GWR模型截距上下四分位数的差值为30.134，大于OLS模型截距的标准误1倍范围(16.722)； 变量SAVI上下四分位数的差值为0.000 002，等于OLS模型SAVI回归参数标准误1倍范围(0.000 002)； 变量PCA2上下四分位数的差值为0.029 04，大于OLS模型PCA2回归参数标准误1倍范围(0.011 86)； 变量B1上下四分位数的差值为0.066 4，大于OLS模型B1回归参数标准误1倍范围(0.022 6)。这说明截距与自变量存在显著的非平稳性，其所选参数均为非全局参数(表6、7)。

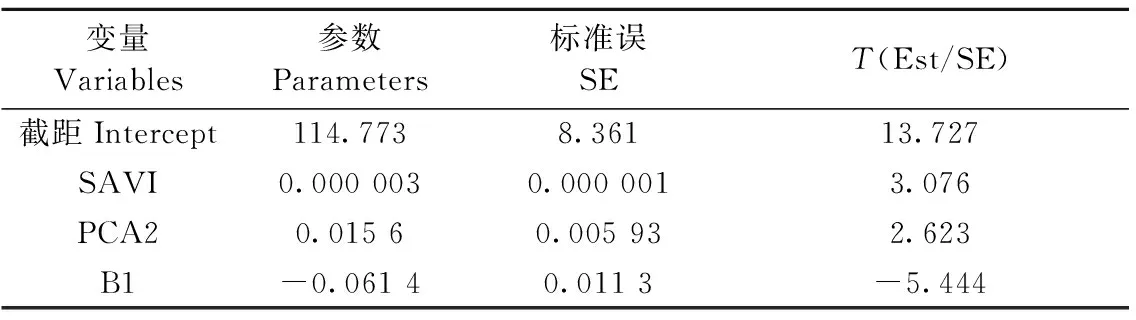
表6 OLS模型全局回归参数描述Tab.6 Descriptive statistics of the global regression parameters of OLS model

表7 GWR模型回归参数描述Tab.7 Descriptive statistics of the local regression parameters of GWR model

3.3.3 模型检验 应用随机抽样的200个小班对OLS、SLM、SEM和GWR模型进行独立性样本检验(表8)。GWR模型预估思茅松林地上生物量的精度最高，SLM、SEM和GWR模型在总体相对误差、平均相对误差、总体相对误差绝对值3个指标上均优于OLS模型，其中SLM和SEM模型的总体相对误差和平均相对误差与GWR模型没有显著差异，GWR模型的总体相对误差绝对值优于SLM和SEM模型。

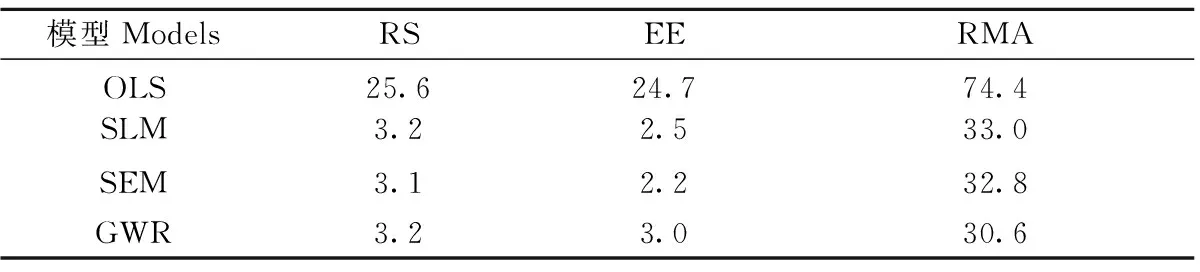
表8 4种模型独立性检验Tab.8 The sample test of independence for the OLS, SLM, SEM and GWR models %

由刀切法残差检验(表9)可以得出，OLS、SLM、SEM和GWR模型在低值阶段(<50 t·hm-2)均出现明显的低值高估现象，但GWR模型的平均残差(ME)和平均相对残差(MRE)的绝对值略低于OLS和SEM模型； OLS模型在大于光饱和值的高值阶段(>100 t·hm-2)出现严重的高值低估现象(ME=65.653，MRE=1.467)，而SLM、SEM和GWR模型的ME和MRE远小于OLS模型，且GWR模型的ME和MRE均为最小。

3.4 生物量反演

基于OLS、SLM、SEM和GWR模型的思茅松林地上生物量反演结果如表10所示。4种模型反演的普洱市思茅松林单位面积地上生物量在66.496～69.222 t·hm-2之间，高于基于森林二类调查数据计算结果53.838 t·hm-2，其中GWR模型估测思茅松单位面积地上生物量为66.496 t·hm-2，地上总生物量为7.82×106t，其预估单位面积生物量值与实测生物量偏差最小，为23.511%。

4种模型反演的普洱市思茅松林生物量空间分布如图4所示。OLS、SLM和SEM 3个全局模型反演思茅松林生物量分布比较均匀，而GWR模型反演思茅松林生物量在空间分布上有一定差异，高生物量(≥100 t·hm-2)主要分布在研究区的江城县和思茅区，低生物量(0～50 t·hm-2)主要集中于澜沧县、西盟县和孟连县。另外，GWR模型相较于OLS模型具有更大的估测范围，说明GWR模型不仅对普洱市思茅松林生物量的估测更为准确，而且能在一定程度上解决高值低估和低值高估问题，减小光饱和点对遥感估测精度的影响。

表9 刀切法残差检验Tab.9 Jackknife method test

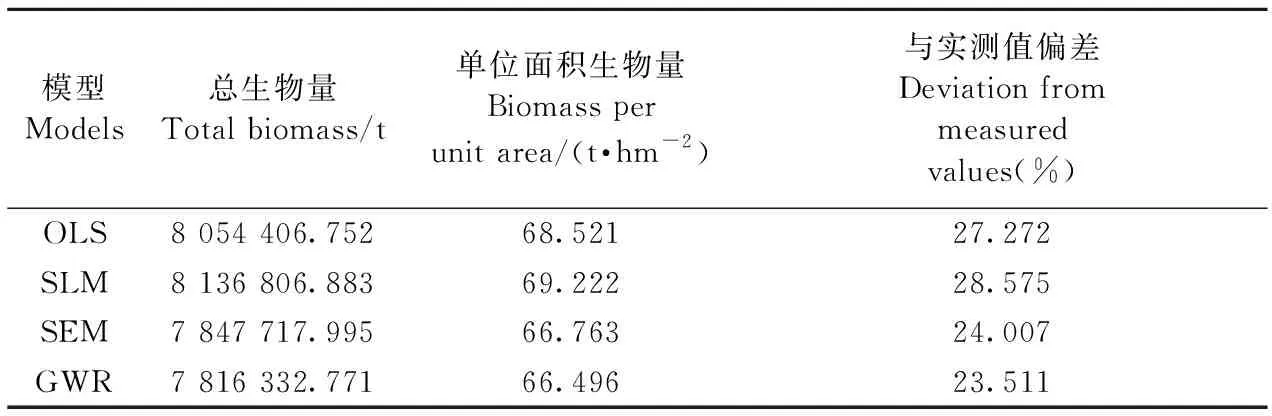
表10 4种模型反演结果比较Tab.10 Model reversion results for OLS, SLM, SEM and GWR models

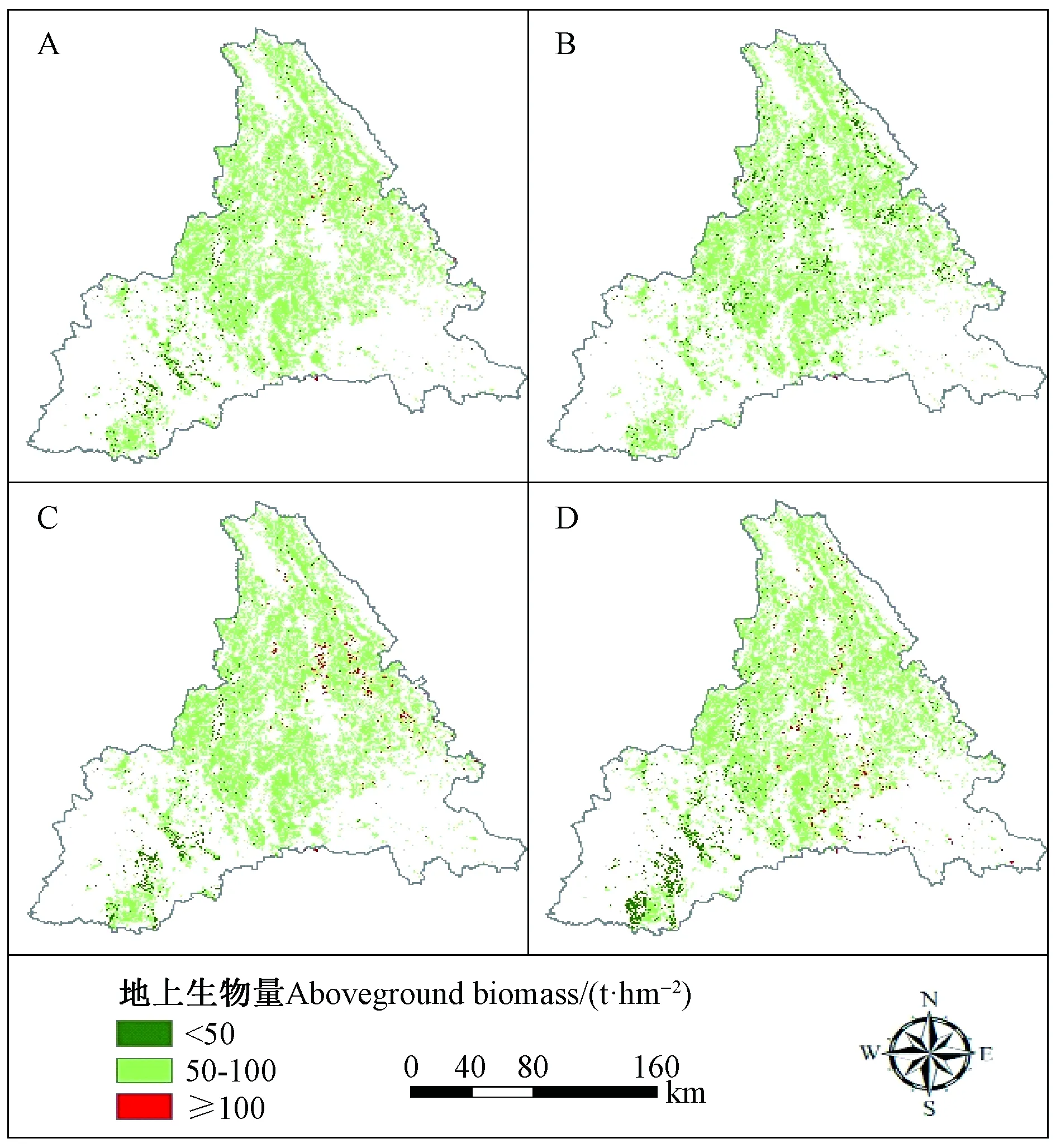
图4 4种模型遥感估测反演结果Fig.4 Inversion result of remote sensing estimation of OLS(A), SLM(B), SEM(C)and GWR(D)models

4 讨论

从思茅松林生物量遥感估测的光饱和点来看，本研究通过二项式函数得出的普洱市思茅松林生物量光饱和点值低于Zhao等(2016)通过半变异函数计算的松类光饱和点值。这可能是因为生物量光饱和点受立地条件、森林结构和树种组成等多种因素影响，普洱市地处南亚热带，山地地形复杂，立体气候明显，垂直差异大，有着更为丰富的气候多样性和生物多样性，且林分结构繁复，森林异质性水平更高，使得普洱市思茅松林生物量光饱和点更接近Kasischke等(1997)计算的热带森林最高光饱和点。

从空间回归模型的表现看，本研究采用OLS、SLM、SEM和GWR模型构建遥感信息模型估测思茅松林地上生物量，得到了较好效果。通过比较发现，局域模型(GWR)的拟合效果和精度明显高于全局模型(OLS、SLM、SEM)，能够减小残差的空间自相关性，且可在一定程度上解决高值低估和低值高估问题。这是因为GWR模型是基于“局域模型”的地理统计方法，针对每个点都精选参数估计并提供空间权重，计算每个样地的空间位置和相邻变量之间的关系，从而使得该模型更加符合传统统计模型中关于残差间相互独立的基本假设，进而减少低值高估和高值低估现象(Fotheringham, 2004)，使得模型的拟合能力和预估能力都更加准确，该结论与闾妍宇等(2017)一致。

此外，本研究使用的地面数据为森林资源二类调查数据，该数据具有分布范围广、数据量大等优点，且其统计数据的精度与各小班的调查允许误差直接相关(王雪军等， 2014)。本研究基于普洱市森林资源二类调查小班数据估测思茅松林生物量光饱和点并构建遥感信息模型，由刀切法残差检验可知，OLS模型在高值阶段(>100 t·hm-2)出现明显的高值低估现象，说明当生物量大于100 t·hm-2后，模型对更高生物量的估计误差更大，在一定程度上与光饱和点的估计值106.3 t·hm-2相匹配，进一步说明森林资源二类调查数据作为森林生物量遥感估测光饱和点的地面数据源的可靠性。此外，4种模型的生物量反演结果较好解释了思茅松林生物量的分布，与基于二类调查蓄积量数据转换得到的生物量数据较为接近，表明森林资源二类调查小班数据在构建生物量遥感模型和森林生物量遥感估测的光饱和点确定方面的数据可用性。

5 结论

1) 采用Landsat8 OLI B1变量进行二项式函数拟合，可用于估算思茅松林生物量光饱和点，其值为106.3 t·hm-2。

2) 基于筛选出的B1、SAVI和PCA2这3个遥感变量构建的空间回归模型，思茅松林生物量估算精度均高于OLS模型，其中以GWR模型精度最高，R2和AIC分别为0.373和4 577.8，有效避免了模型残差的空间自相关性。

3) GWR模型在各生物量分段上的平均残差和平均相对残差低于OLS、SEM和SLM模型，且在思茅松林地上生物量空间分布反演上具有更大的估测范围，能够在一定程度上解决高值低估和低值高估问题，提高思茅松林地上生物量遥感估测精度。