迭代学习在音圈电机轨迹跟踪中的应用研究
贺云波,曾志强,张 昌
(广东工业大学 微电子精密制造技术与装备教育部重点实验室,广东 广州 510006)
1 引言
音圈电机是直线电机的一种,特点表现为体积小、结构简单、推动力大、高速度、高加速度(>20g),正是因其以上特性,故常用于高精度、高加速性能等性能要求的精密定位系统当中[1]。焊线机焊线过程具有高速、高加速、高精度定位的特点,正因音圈电机上述特性,所以焊线机邦头模块采用音圈电机。焊线机的焊线过程包括:电子打火形成金球,音圈电机驱动劈刀高速下降到键合点并接触检测进行焊线,随后进行拉弧操作,最后重复搜寻键合点和焊线的过程[2]。可以看出焊线过程是一个高精度、运动性质重复的过程,其中最关键是其对位置搜寻和拉弧的过程,也即对于规划轨迹跟踪的能力。
为提高控制系统的轨迹跟踪能力,文献[2]等针对轮式移动机器人轨迹跟踪提出前馈+模糊反馈控制算法,其控制效果相对于标准反演控制有所改善,但其模糊规则表的制定依赖过多的先验条件。文献[4]所采用的自适应神经滑模控制消除了抖振现象,提高了系统在轨迹跟踪过程的鲁棒性。上述方法对于轨迹跟踪的误差减小效果有限、且收敛到预期轨迹的速度缓慢又或是过程过于复杂导致设计变量过多。而带遗忘因子的PD型迭代学习控制算法非常适用于这类高重复性的高精密运动过程,而且理论上可以实现高精度的轨迹无误差跟踪。
2 音圈电机的数学模型
当线圈通电时,线圈电流I产生电磁力F带动音圈电机动子运动,与此同时线圈切割磁感线运动会产生反电动势U2,U2大小可以由以下公式得:U2=Blv (1)式中:B—磁场强度;l—磁场中导体的有效长度;v—电机的运行
速度。音圈电机中的等效电路,如图1所示。
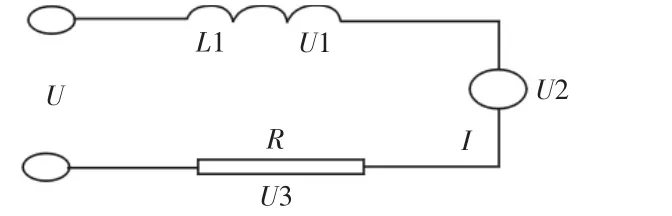
图1 音圈电机等效电路图Fig.1 Equivalent Circuit Diagram of Voice Coil Motor
图中:U—音圈电机两端电压;R—电枢回路电路;I—回路中的电流;L1—电感;U1—电感两端的电压;U2—反电动势。根据基尔霍夫电压定律,可以得到如下的电压平衡方程:

焊线机上的音圈电机是在Z轴上下运动的,依靠电磁力作为驱动力,当电磁力大到可以克服电机动子的静摩擦力时才能使得电机产生直线运动,动子运动时摩擦力即是动摩擦力,其方向与驱动力反向。可以得到如下的力平衡方程:F=ma+cv (3)式中:F—电机中的磁场力;c—阻尼系数;a—加速度。
其中v,a的表达式如下:

则有上述方程可整理得如下:
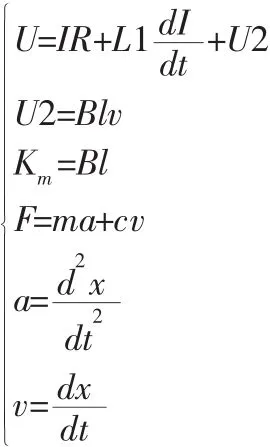
消去中间变量并进行拉氏变换得输入电压和输出位移之间的传递函数:
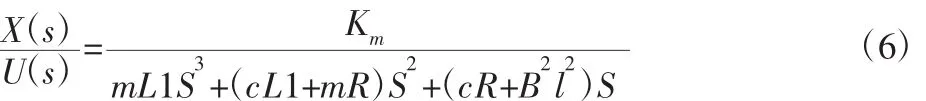
根据上式可得出音圈电机的数学模型框图,如图2所示[5]。
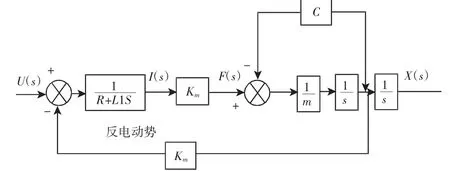
图2 音圈电机数学模型框图Fig.2 Mathematical Model Block Diagram of Voice Coil Motor
3 前馈控制
由于焊线机邦头模块是高精度、高速运动模块,所以如果仅采用反馈控制器没办法保证其高加速度情况下的足够快的响应速度,即会产生时滞[2]。而单纯的前馈控制,只能补偿指定的扰动量,并不能改善控制系统存在的偏差。故采用前馈和反馈相结合的二自由度控制系统[6],相对于反馈控制一定有误差而言,前馈控制在理论上可以做到系统的完全无误差控制。所以前馈控制器的设计对轨迹跟踪问题的意义重大,以下主要阐述关于前馈控制器的设计[7-8]。
3.1 前馈控制器的设计
焊线机邦头的运动不仅要求有高响应能力,其轨迹的跟踪能力对于焊线质量的好坏也有较大的影响。控制要求最好能做到期望轨迹的完全跟踪,迭代学习即是一种能满足轨迹完全跟踪的良好控制方法。
迭代学习主要可以分为开环和闭环以及开闭环三种学习算法[9]。采用的是闭环迭代学习控制其数学描述如下:

上式为闭环迭代学习控制的通式,式中:uk+1(t)—当前的控制输入;uk(t)—前次的控制输入;Γ—学习律;ek+1(t)—当前次的误差。迭代学习效果的好坏与迭代学习控制律密切相关,其中PD型迭代学习控制律是十分经典的控制学习律。则带遗忘因子的PD型闭环迭代学习控制的数学描述如下:

式中:Φc—比例学习矩阵参数;Γc—微分学习矩阵参数;α—遗忘因子;ek+1(t)—此次迭代的误差,且其计算式如下:

而且当t=0时应保证误差为0。
前馈控制器中加入带遗忘因子的PD型迭代学习控制算法后系统结构框图可以表示,如图3所示。
其中虚线方框内为音圈电机的速度环控制。P*(t)—期望轨迹输入;Pk+1(t)—实际轨迹输出;ek+1—本次实际输出与期望输出的误差;uk—前一次的控制输入量;α—遗忘因子。

图3 系统控制框图Fig.3 System Control Block Diagram
3.2 系统描述

式中:k—系统的迭代次数;t∈[0,T]—时间变量;Xk(t)—系统的状态变量;yk(t)—系统的输出量;uk(t)—系统的输入量;A、B、C—常系数矩阵。
由上述系统框图可考虑如下线性系统:
假设系统满足如下条件:
(1)在周期T内存在理想输入ud(t)使得系统能够达到理想输出yd(t)。
(3)[I+ΓcCB]-1为可逆矩阵
3.3 收敛性分析
定理:满足假设 1~3的线性系统(10),采用式(8)的带遗忘因子PD型闭环迭代学习算法,若满足ρ[(1-α)I-ΓcCB]<1且ρ(1-α)<1时,则当k→∞时,在周期T内系统的迭代输出yk(t)收敛于理想轨迹yd(t)。
证明[10]:
由式(8)可得第K+1次控制输入的误差为:

其中:
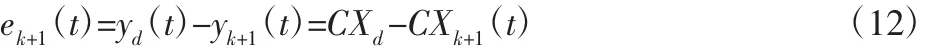
由式(10)解出Xd(t)与Xk+1(t)的表达式代入式(12)得:

因假设初值条件2得:
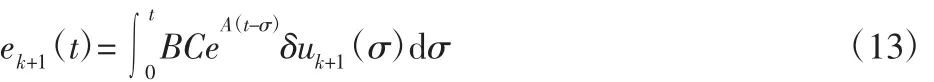
对上式进行求导可得:
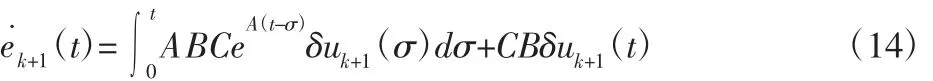
将式(13)和(14)代入式(11)可得:

为表达简便:
令 Q=(1-α),W=ΦcC+CAΓc
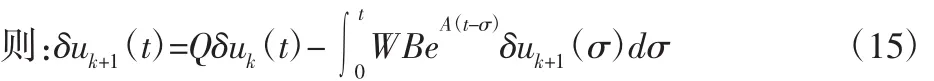
对式(15)两端取范数,由三角不等式得:
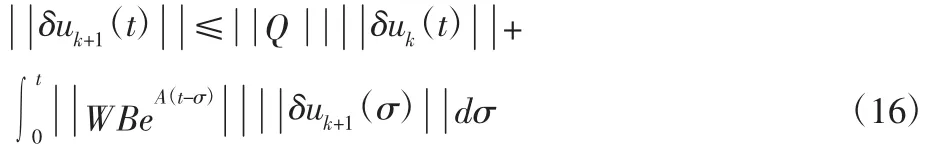

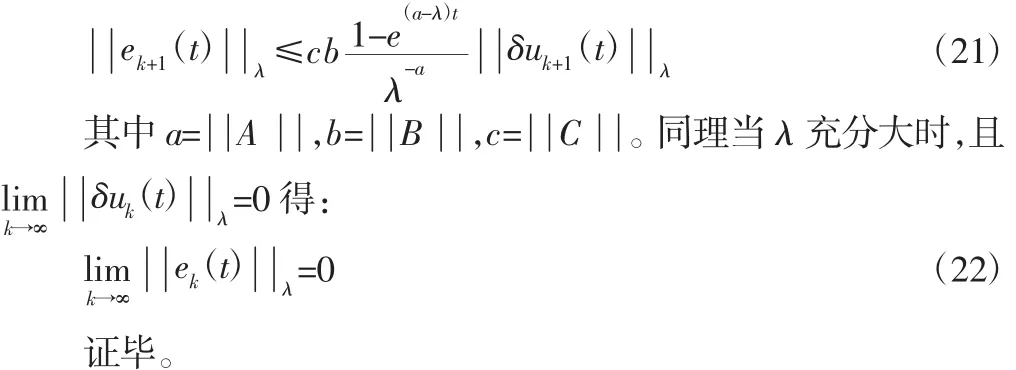
4 仿真研究
在控制系统基础上进行仿真分析,比较开闭环迭代学习控制和无迭代学习控制的轨迹跟踪效果,如图3所示。
依据焊线机邦头模块的高精度要求,确定音圈电机的精度为0.1μm/count,各参数为线圈电阻R=2.3,线圈电感L1=0.9mH,阻尼系数c=4.2N*s*m-1,电机动子质量m=0.035kg,电机力常数km=9.7N/A,带入可得音圈电机的数学模型:
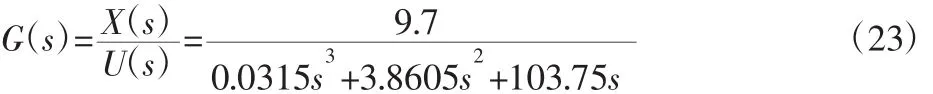
将该电机数学模型代入图3的系统框图中。
经多次仿真实验确定最佳轨迹跟踪效果时的遗忘因子α取值为0.05,Φc取值为0.008,Γc取值为0.049。考虑到邦头模块在实际工况下的位移距离与轨迹曲线,将仿真实验中的期望轨迹设为yd(t)=20000t2。将文中提出的带遗忘因子的PD型迭代学习算法用于控制系统中,并与常见的PID反馈算法和开闭环迭代学习算法作对比。所得到的运动轨迹跟踪效果,如图4所示。可以看出,前馈中使用开闭环迭代学习算法可以提高系统的轨迹跟踪能力,但收敛到规划轨迹的速度较慢,提出的算法相对较优,轨迹跟踪误差小且收敛速度快。
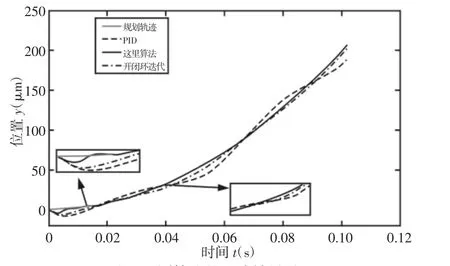
图4 不同算法的跟踪效果对比Fig.4 Comparison of Tracking Effects of Different Algorithms
通过误差大小更直观的观察到,相同迭代次数下的开闭环迭代学习算法与这里算法的跟踪效果差别,可以明显看出迭代算法的误差收敛速度更快,误差收敛值也更小,如图5所示。将算法应用于控制系统后,随迭代次数的增加,达到稳定误差的时间越短,如图6所示。在无迭代时的最大误差为8.4425μm,经10次迭代后的最大误差为5.4903μm,较无迭代减少了34.97%,在经历滞后响应之后时间段误差带小于1.983μm。经100次迭代后的最大误差为2.1874μm,,较10次迭代减少了60.19%,且在滞后响应之后误差带小于0.3024μm,相对10次迭代减少了86.18%,满足了实际生产对邦头定位的精度要求。为直观说明遗忘因子在迭代学习中的作用,迭代次数相同时有无遗忘因子的跟踪误差比较结果,如图7所示。图7可以看出无遗忘因子时的跟踪误差波动范围较大且无法随着迭代次数的增加而收敛到零的邻域内。

图5 不同算法的跟踪误差对比Fig.5 Contrast Charts of Tracking Errors for Different Algorithms
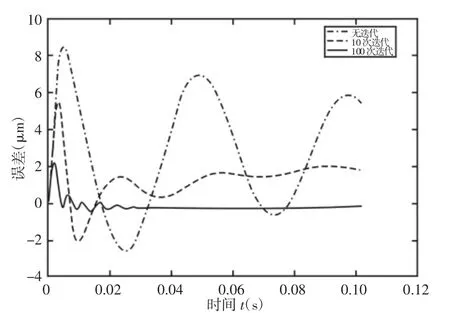
图6 不同迭代次数跟踪误差对比图Fig.6 Contrast Charts of Tracking Errors for Different Iteration Numbers

图7 有无遗忘因子跟踪误差对比Fig.7 Comparison of Tracking Errors with or without Forgetting Factor
5 结论
提出的带有遗忘因子的PD型迭代学习控制算法,在音圈电机的运动控制中可以提高系统的轨迹跟踪能力,在增强响应速度的基础上实现了位置误差的可靠、快速收敛。控制回路的设计贴近实际应用,在迭代初期出现偏差稍大的问题,但是随着迭代次数的增加,位置误差能控制在一定的范围内,对于音圈电机的位置跟踪控制效果明显增强。

