伽利略的科学方法在中学物理中的显化和应用

(广东省汕头市聿怀中学，广东 汕头 515041)

1 伽利略生平

1564年2月15日伽利略·伽利莱(Galileo Galilei)出生于意大利的比萨，他的父亲森里奥·伽利莱是位音乐家。1581年，在父亲的要求下，伽利略进入比萨大学学习医学课程。然而在大学的学习中，伽利略发现自己更喜爱数学，于是不顾父亲的反对，钻研起数学，并于1585年在未取得学位的情况下离开比萨大学。在随后的几年里，伽利略凭借着他的数学才能，发现了一种巧妙测量固体重心的方法，这一发现首次使他在国内外赢得声誉。1589年伽利略受聘为比萨大学教授。1609年伽利略成功制造出了能放大32倍的望远镜，他用这架望远镜观察浩瀚的宇宙，发现了月球并不是光滑的，而是存在山脉和火山口，金星也有类似月球一样的盈亏圆缺的现象，而在木星的周围有四颗绕其旋转的卫星……这些现象都在《星际使者》中被揭示。该书一出版就引起很大的反响，开普勒撰文公开支持伽利略的发现。1611年伽利略在《太阳黑子通信集》中第一次也是唯一一次明确支持哥白尼的天文学说，[1]然而当时势力强大的教会反对哥白尼的“日心说”，1616年教会颁布禁令，禁止他宣传有关哥白尼的学说，伽利略迫于压力只能顺从。在1624到1630年期间，伽利略完成了他最负盛名的著作《关于托勒密和哥白尼两大世界体系的对话》，[2]在这本书中伽利略以对话的形式展示了哥白尼的学说以及自己发现的一些证据，试图以此绕开教会的禁令。但是罗马教会很快发现这本书仍然在支持哥白尼学说，于是下令禁售此书，并且传唤伽利略受审，最后伽利略被判终身监禁，在几位朋友的帮助下，才得以监外执行。但是伽利略并没有停下他研究的脚步，1637年他完成了新著《关于两门新科学的谈话和数学论证》。[3]1642年1月9日为真理而奋斗终生的伽利略在阿圣翠安然离开人世。直至1992年，教皇保罗二世才为伽利略平反冤案，不再把他的著作《关于托勒密和哥白尼两大世界体系的对话》视为异端邪说。[4]

2 伽利略的科学方法在中学物理中的显化

2.1 极限方法

在伽利略所处的年代，当时的科学技术不够发达，无法直接测量瞬时速度，所以无法得出速度的变化规律。[5]伽利略利用数学方法得出结论:若初速度为零且速度均匀变化，则物体的位移大小与时间的平方成正比。只要测出时间和位移，就能验证这个结论猜想是否正确。当时的计时方法是比较落后的滴水计时法，无法直接用来测量自由落体的下落时间，于是伽利略利用斜面运动来“冲淡”重力的影响，他让钢球从阻力很小的斜面滚下，由于加速度变小，所用时间随之增加。经过上百次的实验，伽利略验证了小球沿斜面滚下确实是符合匀加速运动的猜想。当改用不同质量的小球在相同倾斜角度下进行斜面运动时，加速度是一样的。当增大倾斜角度时，加速度逐渐增大，但小球沿斜面滚下的运动并不是自由落体运动。于是伽利略在实验规律的基础上，运用极限的方法进行了外推，如果斜面的倾角慢慢增大，小球将逐渐接近自由落体运动，当倾角为90°时，小球的运动就是自由落体运动，而且此时小球依然做匀加速直线运动，且所有物体的加速度都一样(如图1)。[6]在这个研究的过程中，伽利略把实验和数学、思维方法相结合，极限方法在其中起到了关键的作用，他正是运用极限方法进行合理外推发现了自由落体的运动规律。在此过程中，我们不仅要了解自由落体的运动规律，更要掌握极限的方法。

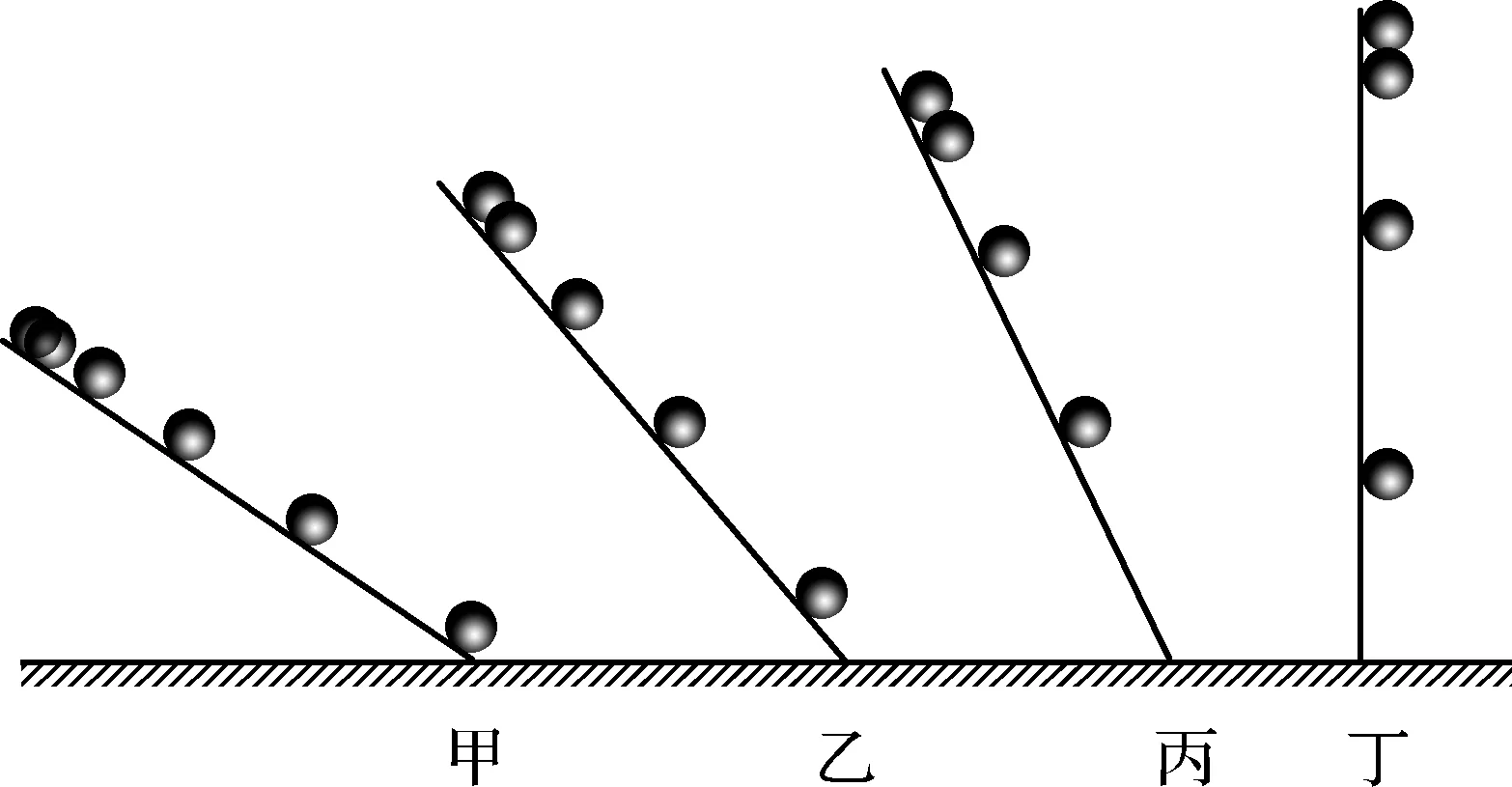
图1

2.2 归谬反证方法

归谬反证是一种逆向的演绎推理，在归谬反证的运用中首先是假定命题为真，即命题成立，然后运用已有结论进行推理演绎，最后论证命题非真，与最开始假设相矛盾，故原命题不成立。伽利略正是运用归谬反证的方法推翻了亚里士多德两千多年来的定论：重的物体下落得比轻的快。[7]伽利略首先假设命题“重的物体下落比轻的快”为真，然后推理：一个重物和一个轻物拴在一起，那么重的物体下落得比轻的物体快，则重物会被轻物拖累，于是整体下落速度应该比重物单独下落的速度小。而换个角度思考，重物和轻物加起来比原有重物更重，则整体下落速度应该比重物单独下落的速度大。很明显，以上两个结论相互矛盾，由“矛盾律”中两个相否定的命题不能同时为真可知，原命题“重的物体下落得比轻的快”不成立。归谬反证的方法不仅应用在物理学科，在其他学科也有广泛的应用。

2.3 理想实验方法

伽利略观察到当小球沿斜面下滑时，速度会增加，当小球沿着斜面上升时，速度会减小。他猜想：如果小球沿水平方向运动，速度应该是不变的，但现实却是小球速度逐渐减小。伽利略认为这是摩擦阻力影响的结果。于是伽利略设计了对接斜面的理想实验(如图2)，[8]如果忽略摩擦力，当小球从斜面一端滚下，它将上升到另一斜面的同一高度。当将另一斜面的倾角逐渐下降，小球依然会上升至同一高度。这时伽利略问道：如果将另一斜面放至水平，那么小球的运动状况将会怎样？很明显小球将一直运动下去而不需要任何外力，也就是说力不是维持物体运动的原因，由此伽利略巧妙地提出了初步的惯性定律。

图2

当然，现实生活中并不可能做到斜面完全光滑、无摩擦，所以伽利略设计的实验是一个理想实验。理想实验是对现实实验的高度纯化，科学家基于常识、经过实验分析进行抽象思维，在理想化的条件下发现新的物理规律已经成为一种常见的手段。理想实验摆脱了现有科学技术水平的限制，在经过纯化的理想实验中，突出主要因素，进行深刻思考，发现解决问题的新途径。

3 伽利略的科学方法在物理解题中的应用

3.1 利用极限方法

利用极限方法解决问题时首先需要分析问题情境，确定各物理量，明确不同物理量间的关系。选取一个与所考察问题相关的物理量，确定其单调性和收敛性，推断其极限情况，如推至极大或者极小等，分析、计算极限情况，发现问题的临界状态，运用极限方法可以巧妙解决问题。

图3

例1：如图3所示，细绳的一端固定在O点处，另一端系着小球。用力F缓慢地推动斜面体，细绳一直处于直线状态，斜面光滑。试问在此过程中斜面对小球的支持力FN和细绳对小球的拉力FT发生了怎样的变化。

解析：首先对物体进行受力分析，物体受重力G、拉力FT、支持力FN，三共点力平衡，通过对图4中矢量三角形分析可知：当拉力FT与FN垂直时，拉力FT达到最小值，所以FT是先减小至最小值后增大，而FN则是不断增大。这道题在运用矢量图的同时运用了极限方法，巧妙地解决了问题。

图4

图5

3.2 利用归谬反证方法

归谬反证的过程就是要证明假设的命题为假，从假定出发，推理的过程要严谨，最终得到与假定相反的结论。

例2：如图5所示，物体A、B叠放在水平面上，物体B在水平拉力F的作用下做匀速直线运动，A、B保持相对静止，请对物体A做受力分析。

解析：本题可以应用归谬反证的方法进行求解，假设A受摩擦力作用，则在水平方向上存在加速度，但是由题设条件可知，物体A与B相对静止，B做匀速直线运动，所以物体A不存在加速度，故与原先假设矛盾，所以物体A不受摩擦力作用。

3.3 利用理想实验方法

一些物理问题往往涉及多个物理过程和物理量有各种变化，直接去分析这些问题有时会感到十分棘手。如果能够根据题目的具体内容，利用理想实验方法进行猜想，则可能会大大简化问题的分析，达到事半功倍的效果。

例3：如图6、图7所示，甲、乙两个球分别静止在光滑平面A、B上，其中A为竖直面，图6中B为水平面，图7中B为倾斜平面，试判断在以上两种情况下A平面对球是否存在弹力作用。

图6

图7

解析：产生弹力的条件是物体直接接触且有弹性形变，但是现实情境中要观察到微小形变是很困难的，我们可以采用理想实验的方法来解决这个问题。首先假设图6中A平面不存在，根据生活经验可知甲球将会保持静止，则A面对甲球没有弹力的作用；同理，假设图7中A平面不存在，则此时乙球将沿着B平面下滑，所以可以判定A平面对乙小球有弹力的作用。