基于剂量权重因子与蚁群算法耦合的核应急路径规划仿真

张广成 何 桃 郑晓磊 陈春花 汪 进 陶龙龙

1（中国科学院核能安全技术研究所 中子输运理论与辐射安全重点实验室 合肥230031）

2（中国科学技术大学 合肥230027）

3（安徽省核应急专业技术支持中心 合肥230031）

4（安徽省国土资源信息中心 合肥230601）

核应急是核安全纵深防御的最后一道屏障，是核能持续健康发展的重要保证［1-2］。放射性核素在大气中扩散迁移形成的辐射场对合理规划救援路径和科学制定应急决策产生重要的影响［3］。

近年来，随着核辐射监测手段的不断提高，针对辐射环境中的路径规划问题，已有不少人做了相关研究［4-5］。国内魏强［6］等采用基本蚁群算法（ACO），规划工作人员在辐射环境中的活动路径；唐邵华等［7］基于核电站辐射分区图创建了核电站控制区内人员行进路线图，并在此基础上基于ACO 建立了核电站控制区内路径优化方法；陶龙龙等［8］综合考虑辐射场剂量率、障碍物和最短路径等约束条件提出一种改进型A 星算法引导的核辐射环境路径规划方法，采用累积剂量作为实际代价，用预估剂量作为估计代价来引导最优路径。Alzalloum［9］研究了放射性污染区域的最小代价路径问题，并利用Dijkstra 算法确定了最小辐射受照路径；Khasawneh 等［10-11］提出了一种局部导航算法，用于辐射环境中的撤离行动；Mól 等［12］采用神经网络和虚拟现实技术评估核电站工作人员所受到的辐射剂量。

辐射环境中的路径规划是应急救援行动的关键，目前大多数研究主要侧重于两点之间的最小剂量优化，而针对不同任务需求，进行时间和剂量多目标约束条件的路径规划问题研究较少，相关的仿真程序不多，实验数据难以获取和比较分析。因此，本文提出了一种剂量权重因子与ACO耦合的路径规划方法，实现了核应急辐射场景下救援路径多目标规划，并选取了某核电厂典型辐射区域进行仿真验证。

1 核应急场景下的路径规划算法

核事故发生后，如何根据不同任务需求进行多目标约束条件下的路径规划是救援行动中的关键问题。由于放射性环境的特殊性，核事故场景下的救援路径规划与其它一般的路径规划问题存在本质的不同，除路径外，还需要考虑剂量等因素，目标函数复杂，约束变量多，需要启发式算法进行求解。本文首先根据辐射环境巡检任务需求构建路径规划数学模型，然后将其转化为多目标旅行商（TSP）问题，运用一种改进的ACO 进行求解。

1.1 ACO介绍

ACO 由意大利学者Dorigo 等［13］首先提出。ACO 的关键要素包括蚂蚁移动规则、信息素更新规则和迭代终止准则等［14-15］。

1.2 剂量权重因子

辐射环境中的N个巡检救援节点，任意两点间的剂量值通过环境中的探测值和历史记录数据，借助数据重构软件，构造出整个放射性空间中的剂量场［16-17］。本文根据ACO 规则，对问题进行了转化，将两个节点之间的剂量值转化为等效路径长度，设置剂量权重因子，进而表征剂量大小对蚂蚁路径选择的影响。

等效路径长度计算见式（1）。

式中：Aab表示巡检救援人员从起点a到终点b所受总剂量，单位：mSv，即等效路径长度；Akl表示巡检救援人员从k 点到l 点整个路程中所受剂量，单位：mSv。

剂量权重因子计算见式（2）。

式中：αkl表示剂量权重因子，是剂量影响蚂蚁选择路径非常重要的参数，其数值为k 点到l 点之间剂量和总剂量的比值，无量纲。

2 数学建模及算法实现

2.1 数学模型

一个多目标优化（MOP）［18］可表示为式（3）。

式中：Ω 为决策变量空间，F：Ω →Rm由m 个实数函数组成，Rm称为目标空间，可行解目标集合定义 为{F(x)|x ∈Ω}， 令 u，v ∈Rm， 对 于 每 个i ∈{1，…，m}，当且仅当ui≤vi时，称u 支配v；若不存在x ∈Ω，使得F(x)支配F(x*)，则称x*∈Ω是帕累托最优解（Pareto optimal），F(x*)称作帕累托最优目标向量（Pareto-optimal objective vector），也就是说，在帕累托最优点的一个目标上的任何改进都必导致至少另一个目标的恶化。所有帕累托最优解的集合称为帕累托集（Pareto set），帕累托集对应的目标向量集合称为帕累托前沿（Pareto front）。

通过将上述问题转化为TSP 问题进行求解，给定了N 个巡检救援点之间的距离矩阵和剂量矩阵，这个问题可以描述为式（4）。

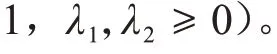
2.2 算法实现

本文采用剂量权重因子与基于分解的多目标ACO（MOEA/D-ACO）［19］耦合进行求解，通过选择N 个权重向量λ1，λ2，…，λN将一个多目标优化问题分解转化为N个单目标子问题，每个子问题i对应的权重向量为λi，其对应的子问题记为g(x|λi)。相应地，MOEA/D-ACO 用N 个蚂蚁求解这些子问题，每个蚂蚁分别负责一个子问题，即蚂蚁i负责子问题g(x|λi)。蚂蚁i 的邻域B(i)包含T 个最相邻的蚂蚁，即这些蚂蚁的权重向量与蚂蚁i的权重向量距离比其他蚂蚁对应的权重向量到蚂蚁i的距离都小。N个蚂蚁依据其权重向量聚类被划分为K个子群，每个子群负责逼近帕累托面一部分。如图1，给出的算例中，目标数m为2，蚂蚁数N为14，子群数K 为2，邻域大小T 为5。该多目标优化问题被分解成14个单目标子问题。蚂蚁i负责优化子问题i。第一个子群由蚂蚁1到7组成，其他蚂蚁构成第二个子群。每个蚂蚁有5个邻居，如蚂蚁6的邻居为蚂蚁4、5、6、7和8。算法相关参数含义如表1所示。

表1 算法中主要参数的含义Table 1 Implication of main parameters of algorithm

2.2.1 信息素更新策略

若Π 为当前代中被子群j 构造出的经过节点k到l，且被加入精英档案（EP）中解。子群j 中所有蚂蚁经过节点k 到l 之间路径对应的信息素浓度计算见式（5）。

2.2.2 状态转移规则

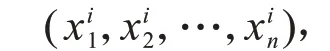
2.2.3 启发式因子

为了使得蚂蚁尽量往终点方向移动，引入了启发式因子概念，表征移动到相连节点的期望程度。在不考虑辐射剂量的情况下，启发式因子一般取节点与目标点之间直线距离的倒数。在辐射场中，考虑到辐射剂量率的影响，在没有障碍的情况下起点与终点之间的直线不一定是最优路径。出于剂量最优的考虑，蚂蚁应尽量远离高辐射区域，其排斥程度应与辐射剂量率成正比。因此，对启发式因子进行修正，可得到式（8）。

3 仿真验证

基于FDS 凤麟核能团队自主研发的仿真平台实现算法并进行仿真模拟［20-24］，选取国内某一压水堆核电厂典型辐射区域作为研究对象，选择场景中12 个可连通的巡检救援任务点（表2），规划在一次巡检救援中的行动路径。

首先根据实际应用场景将20 m×10 m的辐射区域划分为800×400 的网格，并定义各个网格为实体，取1.6 m标高下水平切面上离散的网格点代表该平面内二维剂量场分布［25］，如图2（a）所示，利用实际监测数据和高斯平滑方法可视化剂量场。然后利用改进的ACO，分别选取不同的时间、剂量约束重要度参数，在同一辐射环境下进行路径规划，显示路径并计算全程行进距离和总剂量代价。

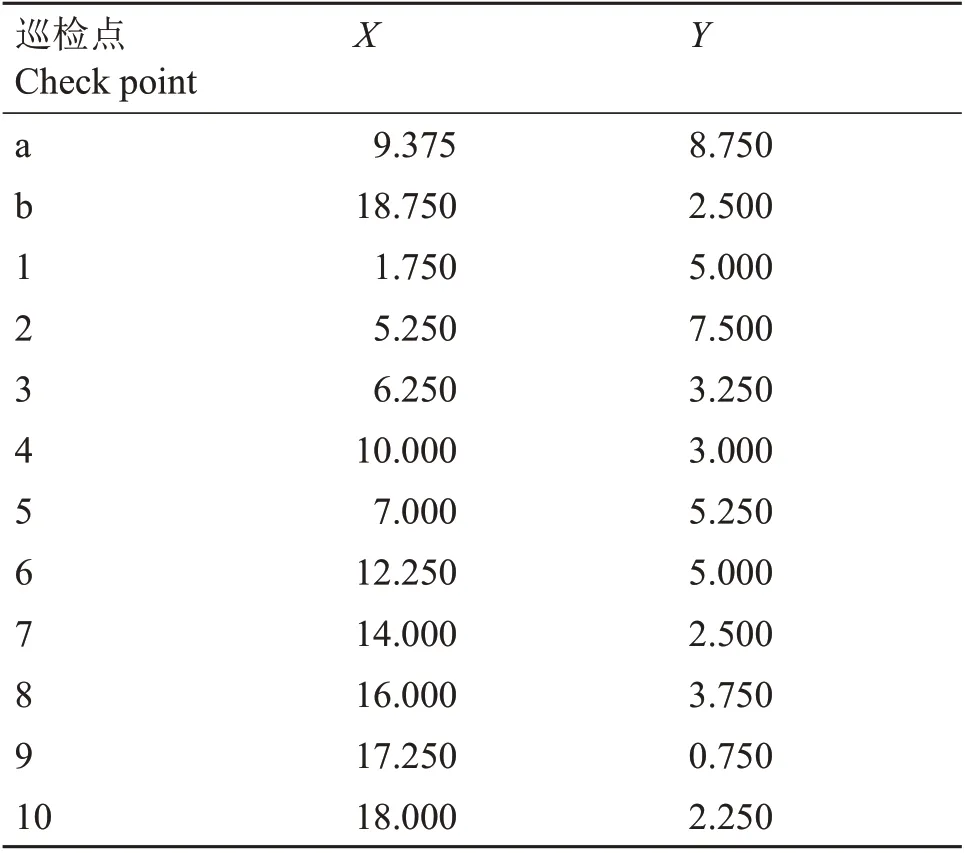
表2 辐射场巡检点坐标Table 2 Coordinate of check points in radiation field

图2 所示，以a 节点为巡检任务起点，b 节点为终点，考虑行程时间与辐射剂量多目标约束条件，来仿真验证距离最优（图2（b））、剂量最优（图2（c））以及折衷最优（图2（d））任务环境下巡检路径规划方案。表3为仿真数据对比表，通过对比不同任务环境下仿真模拟结果可知：当λ1=1、λ2= 0，基于巡检时间最短考虑，路径长度虽短，却使巡检人员所受辐射剂量偏大；

当λ1= 0、λ2= 1，基于巡检人员所受辐射剂量最优考虑，路径长度增加了，但是所受剂量明显下降；λ1= 0.5、λ2= 0.5，综合考虑辐射剂量和路径长度，得到折衷方案。

利用本案例验证本文算法与文献算法［6］优劣，结果见图3。

表3 仿真数据对比Table 3 Data comparison of simulation

图3（a）所示，如果只考虑巡检距离最优，通过两种算法对比分析，文献算法在第19代收敛，最优解为159 m；本文算法在第9 代收敛，最优解为133 m，方案优于前者。图3（b）所示，如果仅考虑巡检人员所受剂量最优，通过两种算法对比分析，文献算法在第13代收敛，最优解为39 mSv；本文算法在第8 代收敛，最优解为22 mSv，方案优于前者。

表4所示，同时考虑时间和剂量因素，寻找最优折衷方案，文献算法在第19 代趋于收敛，最优解为（140 m，34 mSv），本文算法在第9 代收敛，最优解为（139 m，30 mSv）。

表4 本文算法与文献算法仿真模拟数据对比Table 4 Data comparison of paper algorithm and literature algorithm simulation

4 结论

本文以ACO 为基础，考虑剂量权重因子，提出了辐射剂量、行动时间约束的多目标路径优化方法。仿真验证结果表明，采用剂量权重因子与ACO 耦合的方法充分考虑了辐射环境特点，能够在不同核事故状态下，基于时间和剂量的重要度进行不同的辐射权重分配，可实现路径的合理规划。通过与文献中算法对比，本文算法在收敛速度和求解精度上均优于文献算法。本文方法可为核辐射环境下工作人员的维修与巡检安全、事故情况下的快速应急救援决策提供技术支持。