主要战略方向电子防空体系作战效能评估

王 强，严振华，孙和强

(空军预警学院，湖北 武汉 430019)

0 引 言

从贝卡谷地之战开始，电子防空逐步成为防空作战的重要组成部分。目前电子防空已经成为了防空行动中首当其冲、全程使用的作战手段。主要战略方向的电子防空能力建设已经成为争夺战场主动权的重要因素，研究此问题具有现实意义。

传统基于模糊层次分析法的效能评估对电子防空体系的作战效能进行了初步的评估，但总体来说研究还不够深入，存在评估过程过于简单、评估方法缺乏科学性依据的问题。为此,本文在对前人成果进行充分学习的基础上提出了一种新的评估方法，首先构建电子防空作战效能评估指标体系；其次，利用层次分析法确定各指标权重，基于模糊理论建立模糊评判模型；最后，对主要战略方向电子防空体系作战效能进行分析计算。

1 评估指标体系构建

电子防空作战效能评估指标体系构建的关键是选取能够反映实际问题的指标,但复杂的电子防空体系构成，使指标体系的构建变得较为困难。因此，在充分考虑影响电子防空作战效能的各项因素的前提下，选取指挥控制能力、电子战能力和综合保障能力作为评估作战效能的3个准则。它们从多角度对电子防空的作战效能进行了较为科学的描述，能够有效反映电子防空作战效能的主要环节。为了更加深入地研究问题，在3个准则下再细化为9个具体指标，由此构建包括目标层、准则层和指标层在内的电子防空体系作战能力评估的3层指标体系，如图1所示。其中，电子防空体系作战效能的评估为最终目标；影响作战效能的指挥控制能力、电子战能力、综合保障能力是指标体系的中间层；9个具体指标即为指标体系的末端层，分别为态势掌控能力、指挥决策能力、效果评估能力、电子支援能力、电子干扰能力、电子防护能力、战勤保障能力、装备保障能力和后勤保障能力。

图1 电子防空作战效能评估指标体系

2 基于AHP法的权重确定[1]

层次分析法(AHP)是一种国际上认可程度比较高的评估分析方法，适用于对目标结构复杂、缺乏初始数据的问题进行分析。

权重确定的步骤如下：

(1) 根据建立的评估指标体系和相对重要性等级表在不同情况下构造准则层的判断矩阵：S=(sij)k×k，sij表示si对sj的重要性，k为准则层元素个数。

(2) 采用本征向量法对判断矩阵A进行求解，得到最大实特征根λmax和其对应的归一化特征向量。

(4) 当RC<0.1时，判断矩阵S符合一致性要求，其对应的归一化特征向量即为准则层的权重W；反之，返回第1步，重新构造判断矩阵，进行求解和检验。

(5) 同理可得指标层相对于准则层的权重W1，W2，…，Wk。

3 基于模糊综合评判法的效果评估[2]

模糊综合评判就是以模糊数学为基础，应用模糊关系合成原理，对受到多种因素制约的事物或对象，将一些概念不清、难以定量分析的因素进行定量化，按多项模糊的准则参数对备选方案进行综合评判，再根据综合评判结果对各备选方案进行比较排序，选出最好方案的一种方法。

对于多层次因素构成的电子防空体系作战效能评估，可以构建多级综合评判系统，如图2所示。

图2 模糊综合评判模型

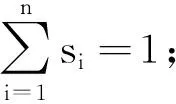
f:U→F(V),∀ui∈U

(1)

(2)

式中：0≤rij≤1；1≤i≤n；1≤j≤m。

由f诱导出模糊关系，可以得到模糊矩阵：

(3)

评价集分为3等，记为V={E,D,K}，其中“E”代表“较好”，“D”代表“一般”，“K”代表“较差”，并将评价等级分值定为E=0.9,D=0.6，K=0.2。

系统评估主要是确定评价矩阵R，关键是隶属度的确定。本文采用专家打分，根据模糊统计法，给出隶属度的估算值方法。

4 实例应用与分析

根据图1构建的电子防空体系作战效能评估指标体系，基于层次分析法和模糊综合评判法，对作战效能进行评估计算。

4.1 指标权重计算

将目标层与准则层元素的重要性对比，可以得出判断矩阵如表1所示。

电子防空体系作战效能权重值为W=(0.614,0.268,0.118)T，其中λmax=3.07,IC=0.035,RC=0.06≤0.1，满足一致性检验。

表1 判断矩阵S-Bi

同理，可计算相应的准则层对应的指标层权重值为：

W1=(0.23,0.283,0.487)T

W2=(0.234,0.218,0.548)T

W3=(0.457,0.4,0.143)T

4.2 模糊综合评判

这里，以“态势掌控能力”为例，采用专家打分方式，计算评价结果。专家分数为10分制，每位专家根据实际情况，选取φ={1，2，3…，10}中的任意一个为评价指标进行评分。选定若干位专家参与评分，并对分数进行整理，即可得到元素集U={U1,U2,…，U10}，(依次表示1、2、…、10分)。根据模糊统计计算，得到分数1至10所对应评价集中的“较好”“一般”“较差”的隶属度为：

V1=(0,0,0,0,0.3,0.6,0.7,0.8,0.9,1)T

V2=(0,0,0.2,0.8,1,0.7,0.3,0.1,0,0)T

V3=(1,1,0.9,0.8,0.2,0,0,0,0,0)T

假定有30位专家参与“态势掌控能力”指标项评分，其评分结果表示为U=(0,0,1,3,6,8,8,3,1,0)，则：

UV1=(0,0,1,3,6,8,8,3,1,0)(0,0,0,0,0.3,0.6,0.7,0.8,0.9,1)T=15.5

UV2=(0,0,1,3,6,8,8,3,1,0)(0,0,0.2,0.9,1,0.7,0.3,0.1,0,0)T=17.2

UV3=(0,0,1,3,6,8,8,3,1,0)(1,1,0.9,0.8,0.2,0,0,0,0,0)T=4.5

将结果进行归一化处理，得到评价结果为：

r11=(0.417,0.462,0.121)

同理，可得“指挥控制能力”其他两项三级指标的评价结果,并由此得到模糊判决矩阵：

基于“态势掌控能力”的指标权重值W1=(0.23,0.283,0.487)T,采用模糊判决法，则B=S∘R，求得其模糊判决因子为：

同理，可得其他两项二级指标的模糊判决因子分别为：

B2=(0.548,0.251,0.19)

B3=(0.417,0.457,0.19)

对B1、B2、B3进行归一化处理后，可得电子防空体系模糊判决矩阵为：

基于电子防空体系作战效能评价指标权重W=(0.614,0.268,0.118)T，同理，可以运用B=S∘R，得系统评价矩阵：

M=WT∘B=(0.614,0.268,0.118)T∘

据此计算出系统评价结果M=(0.507,0.295,0.198)。

由此，可以得到电子防空系统作战效能的最终评估结果为：

0.507×0.9+0.295×0.6+0.198×0.2=0.672 9

根据这个结果对比来看，电子防空体系总体作战效能大于0.6，基本能够满足防空作战的实际作战需求。

5 结束语

作为主要战略方向防空作战的主要手段之一，电子防空已经得到了广泛应用，如何评价电子防空体系作战效能显得非常重要。本文通过层次分析法与模糊理论相结合的方式，对主要战略方向电子防空体系作战效能进行评估计算，最终得出的结果具有一定的借鉴意义。但是，由于目前电子防空作战的实际作战数据积累较少，仅仅依靠专家评判，难以达到较好效果，还需要在实际作战行动中进行不断检验。