基于虚拟科氏力相位特性的硅MEMS陀螺自动模态匹配及闭环检测

彭友福，赵鹤鸣，卜 峰，程梦梦，喻 磊，徐大诚，郭述文

(1.苏州大学电子信息学院，江苏苏州 215006;2.华东光电集成器件研究所，安徽蚌埠 233000)

0 引言

MEMS谐振陀螺由于体积小、质量轻、功耗低、可批量生产、易于与现有集成电路制造工艺相结合的优点，广泛应用于航空航天、导航制导、消费电子、汽车电子、机器人、工业控制等许多领域［1］。

MEMS谐振陀螺是用来测量角速度或者角度的一种惯性传感器。模态匹配时(陀螺驱动、敏感模态谐振频率相等)，陀螺的角速度检测灵敏度最高、标度因子最大，可以极大地改善陀螺的检测性能。受制造工艺精度和材料残余应力的影响，加工后陀螺的驱动轴和敏感轴不完全垂直，实际的驱动模态和敏感模态谐振频率和设计的不一样，导致两模态的谐振频率不相等，降低了科氏力的能量转换效率以及有效的品质因数［2］;另外，环境温度对两模态谐振频率的影响不完全一致，因此，研究人员把模态匹配控制方法作为提高硅MEMS陀螺性能的重要手段［3］。

一些方法是通过特殊的制造工艺来调节结构谐振频率，如激光微调、在特定区域淀积附加材料等［4］。这种方法是一次性的，在MEMS结构加工好后谐振频率是固定的，受环境温度、残余应力等的影响较大，无法实现准确、自动的模态匹配。

其他方法利用静电负刚度效应，通过施加直流调谐电压到陀螺的调谐电极上来减小陀螺的刚度系数，从而减小谐振频率，实现模态匹配。由于这些静电负刚度方法不需要改变陀螺结构，因而从新思路到最后的电路验证更容易实现，实验周期短，更适于批量生产;另外，这些方法可以实现自动频率调节因而受环境的影响较小，鲁棒性更强。因此，利用静电负刚度效应的方法得到更为广泛的应用。其中，文献［5］在指定的调谐电极上使用一个固定的直流电压来减小两模态之间的谐振频率差。显然，当频差随环境温度变化时，固定电压却无法改变，无法跟上频差的变化。利用陀螺模态匹配时正交误差的幅频特性或相频特性来控制调谐电压，可以实现自动模态匹配［6－11］。但是，这两种方法在有角速度输入的时候都失效了，因为此时敏感输出混合了科氏信号和正交误差。而且，把正交误差抑制得非常小时，这两种方法也没法工作了，因为需要一定的正交误差幅度或者相位作为自动模态匹配的度量。文献［12］使用神经网络通过大量样本训练实现了实时模态匹配，这种方法需要大量的实验测试，而且系统较为复杂。文献［13］介绍了基于外加静电力的相位特性实现了双质量全解耦陀螺的自动模态匹配方法，其性能测试基于LabVIEW FPGA仪器，比较了模态匹配前后标度因子的变化，但是未报道零偏不稳定性的比较结果。本文采用这种方法对一种新型的十六边形陀螺［14］进行实验验证，基于PCB电路进行性能测试，不仅比较了模态匹配前后标度因子的变化，还比较了零偏不稳定性的变化。

利用虚拟科氏力的相位特性进行自动模态匹配的方法与利用正交误差的相位特性进行自动模态匹配的方法类似，这里利用固定虚拟科氏力与敏感输出之间的相位差来判断模态匹配。不同的是，利用正交误差相位特性进行模态匹配的方法在科氏力存在时无法正常工作，即无法检测科氏力，而本文介绍的方法可以在实现自动模态匹配的同时实现科氏力的检测，即可以实现实时模态匹配。同时，不需要借助正交误差来控制调谐电压，即允许将正交误差抑制为0。

1 理论分析

1.1 陀螺结构

研究过程中使用的蜘蛛网状DRG如图1(a)所示。谐振器由10个同心的16边形蛛网环组成，通过8个辐条交替连接到中心锚点。最外圈环的直径为3 900 μm，中心锚点的直径为1 700 μm。质量块悬挂在从内到外的奇数层环与偶数层辐条上，以获得较大的检测质量。谐振器由16个外部电极包围，用于频率调谐和正交归0，电容间隙为7.5 μm。每个环上有8个分离的多边形槽，插槽内插有双电极，以增加驱动和敏感的转换面积。最内部两层插槽也插入了调谐电极以增加调谐能力。由COMSOL仿真的该陀螺工作模态振型图，如图 1(b)所示［14－15］。

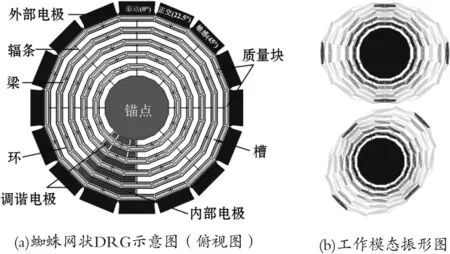
图1 十六边形陀螺结构与两模态振形

1.2 基于虚拟科氏力相位特性的模态匹配方法

敏感模态受到科氏力和正交力的作用，科氏力是由角速度产生的。而正交力产生的正交误差会对控制系统的零偏不稳定性产生很大的影响，特别是模态匹配时，正交误差也被同时放大了。因此，应当尽可能抑制掉正交误差。

在正交刚度调节电极上施加直流电压VQNN，把正交误差抑制到非常小的稳定状态后，再引入一个由FPGA电路产生的与科氏力同频同相的虚拟科氏信号，作用在敏感模态的力反馈电极。此时，可以把虚拟科氏信号与敏感模态输出的相位差电压作为模态匹配的一个度量，来控制频率调谐电压调节指定模态的谐振频率，从而使系统处于模态匹配状态。设计的基于虚拟科氏力相位特性的自动模态匹配控制框图如图2所示。在质量块上加载1 MHz的载波，把陀螺振动信号调制到高频载波。陀螺敏感检测信号经过C/V放大把电容信号转化为电压信号，经过HPF滤除低频干扰信号后，通过二极管解调、低通滤波得到陀螺敏感输出信号。

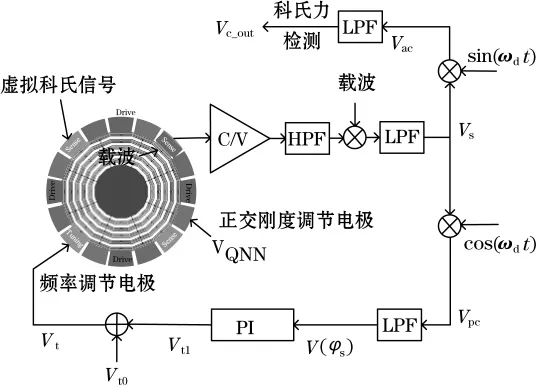
图2 基于虚拟科氏力相位特性的自动模态匹配控制示意图

设驱动激励信号为Fd=Adcos(ωdt)，式中Ad为驱动信号幅度，ωd为驱动模态谐振频率。驱动模态通过AGC和PLL锁相环稳定工作在驱动模态谐振频率点后，科氏力为与驱动激励同频同相的信号，可通过FPGA 电路生成虚拟科氏信号 Vvc=kvc·cos(ωdt)［16］。kvc是控制虚拟角速度大小的比例因子，为可调的定值。因此，引入到陀螺敏感模态力反馈电极激励敏感模态振动的固定虚拟科氏力为Fvc，Fvc=Vvc·kvf=kvcs·cos(ωdt)。式中，kvcs=kvc·kvf，kvf为敏感模态电压到静电力的转换系数。

陀螺敏感模态输出信号为Vs，经过解调、低通滤波，得到Vs与Fvc的相位差电压V(φs)，把它作为模态匹配的一个度量，来控制调谐电压Vt。推导如式(1)、式(2)所示。

式中:Vpc为Vs经过cos(ωdt)基准信号解调后得到的信号;φs为 Vs与虚拟科氏力的相位差;Vqsin(ωdt－φs)为由驱动模态振动耦合到敏感模态引起的正交误差;Vq为正交误差信号的幅度;Vccos(ωdt－φs)为科氏力作用在敏感模态引起的敏感模态振动，Vc为它的幅度;Vdcos(ωdt－φs)为虚拟科氏力作用在敏感模态的输出;Vd为它的幅度;LPF表示低通滤波器。

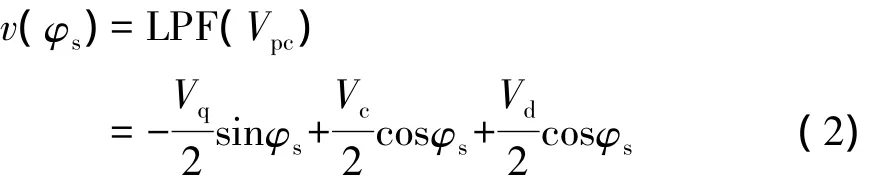
假如将正交误差抑制到很小甚至为0，那么式(2)可以改成式(3):

在陀螺振动过程中，V(φs)作为PI控制器的输入，通过PI控制产生直流电压，把该直流电压施加到谐振频率较高的那个模态的调谐电极上，就可以降低其谐振频率，从而使2个模态的谐振频率相等。Vt是最终施加到调谐电极的直流调谐电压，Vt=Vt0+Vt1。式中:Vt1是PI控制器输出的直流电压;Vt0是为了增加频率调节范围而输入到加法器的固定直流电压。

当驱动模态与敏感模态匹配时，相位差φs=90°，V(φs)=0，也只有当 φs=90°时，V(φs)才等于 0，根据这个值来判断模态是否匹配。否则，V(φs)将使PI控制器持续地调节调谐电压，直到 V(φs)为0。

由于虚拟科氏力与科氏力是同频同相信号，在不同的解调通道可以分别得到他们的相位和幅度。因此，这种基于虚拟科氏力相位特性的模态匹配方法在模态匹配的同时，也能检测角速度。所以，另一路解调将得到输入角速度产生的科氏输出。其中，乘法解调、低通滤波后分别得到 Vac、Vc_out，如式(4)～式(5)所示。

由式(5)可知，在模态匹配时，φs=90°，正交误差项为0。式(5)可写成:

式中，科氏力检测Vc_out存在一个固定的偏置电压Vd/2，在角速度输入后减去这个偏置即可。

因此，模态匹配时，通过Vc_out可以得到我们需要的角速度信息。

1.3 科氏力反馈检测

为了增加科氏力检测范围，在模态匹配基础上设计科氏力反馈闭环检测(科氏力平衡)，控制系统如图3所示。其中Ksf是一个衰减因子，可以调节闭环检测的标度因子。S是拉普拉斯方程的复变量。ms为陀螺敏感模态质量块的质量。Cs和Ks分别表示陀螺运动的阻尼系数和刚度系数。Kxc、Kcv分别表示检测电路振动到电容、电容到电压的转换系数。

图3 模态匹配与科氏力反馈闭环检测控制系统示意图

与大部分的力平衡闭环检测系统原理类似［17］，通过对敏感输出进行乘法解调、低通滤波之后得到Vc_out。通过PI控制器把Vc_out控制在一个固定参考值Vref，PI控制器输出再乘以一个与科氏力同频同相的基准信号cos(ωdt)，以抵消科氏力，从而拓展可检测角速度的范围。由于依靠输入的虚拟科氏力来判断模态匹配，不能把输入虚拟科氏力完全抵消掉，故这里通过PI控制器把 Vc_out控制在Vref。所以 Vc_out不再是角速度检测点。而PI控制器的输出V'c_out抵消了科氏力，其与科氏力大小相等，方向相反，遂把V'c_out作为角速度检测点。

2 仿真分析

2.1 谐振频率与调谐电压的关系

根据陀螺的静电负刚度效应，在陀螺调谐电极上施加直流调谐电压，可以降低谐振频率，并且谐振频率和调谐电压的关系近似于平方关系，即有公式如式(7)所示。

式中:ω为陀螺驱动或者敏感模态的谐振频率;ω0为其初始谐振频率;Vp为电极与质量块间的调谐压差;b为根据实际测试的频率－电压关系得到的拟合参数。

通过扫频方法测量陀螺驱动和敏感模态在不同的调谐电压下的谐振频率，如图4所示。当调谐电压位于5.6 V附近时，两模态谐振频率相等。根据驱动模态频率与电压的拟合曲线，可以令b=5 489.189。

图4 谐振频率与调谐电压的关系

2.2 仿真结果

为了验证所提出的基于科氏力相位特性的自动模态匹配以及科氏力闭环检测的可行性，搭建了simulink仿真模型。所用陀螺主要参数如表1所示。

表1 陀螺主要参数

根据搭建的simulink仿真模型进行仿真，结果如图5所示。图5(a)是开环检测时模态匹配的仿真结果，模态匹配后，调谐电压最后稳定在5.6 V，驱动模态谐振频率稳定在敏感模态谐振频率点。这里所用的陀螺驱动模态谐振频率高于敏感模态谐振频率，所以调谐电压加在驱动模态调谐电极。

模态匹配时与闭环检测仿真结果如图5(b)。其中，模态匹配过程与图5(a)相同。模态匹配调谐电压基本稳定后，在0.6 s时加入科氏力闭环检测，将敏感模态科氏输出振幅稳定控制在－0.2 V，科氏力反馈电压幅度为－0.5 V，驱动模态频率与调谐电压抖动一下后迅速稳定到模态匹配状态。由图5模态匹配开环及闭环检测的仿真结果可知，第2节中设计的基于虚拟科氏力相位特性的模态匹配及其闭环检测控制方法可以实现。

3 实验测试结果

根据所设计的自动模态匹配控制及其闭环检测方法，在图6所示的基于FPGA的数字电路中实现了该控制系统。证明了所提出方法是可行的，能够有效、稳定地实现实时模态匹配，并对控制系统的性能进行了测试。

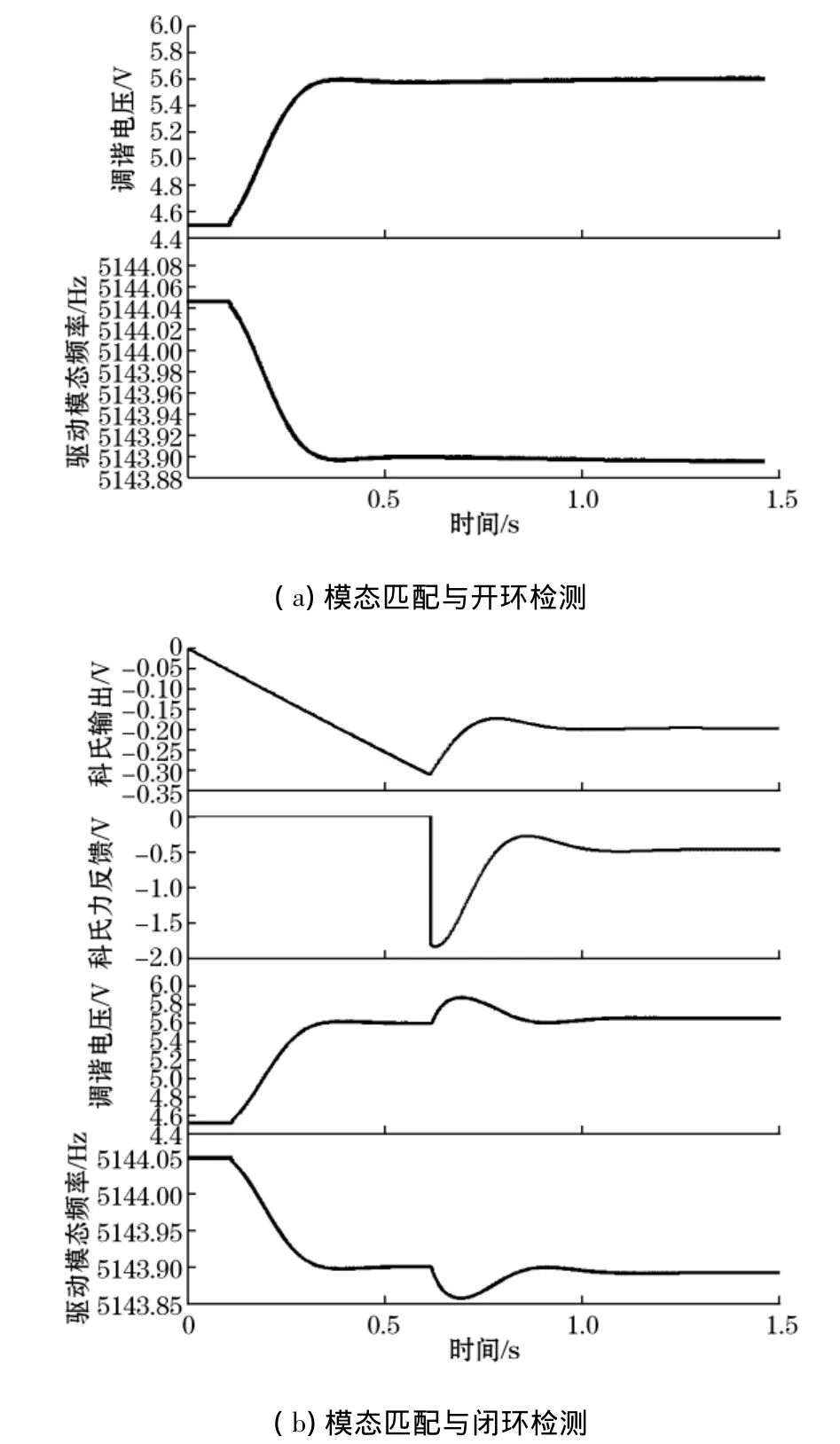
图5 simulink模型仿真结果

图6 实验所用控制电路实物(PCB电路)

3.1 正交刚度校正

由结构不对称和工艺误差导致的正交误差，对硅MEMS陀螺的零偏不稳定性影响非常大，同时，有效地减小正交误差也是本文提出方法能够实现的前提。正交误差越小，零偏也越小，检测精度就更高，正交误差对模态匹配的影响也就越小。

通过正交刚度调节方法，调节施加在正交刚度校正电极上的直流电压，可以将正交误差降低至50 mV以下，满足所提出的模态匹配方法的要求。正交误差抑制效果如图7所示，当VQNN为10.68 V附近时，正交误差被抑制地非常小。

图7 正交刚度校正

3.2 模态匹配实现

在将正交误差信号抑制得非常小且稳定之后，在陀螺敏感模态的力反馈电极引入虚拟科氏力使敏感模态产生振动。此时通过虚拟科氏力及其在敏感模态产生的振动信号之间的相位差来实现模态匹配。模态匹配前、后结果分别如图8(a)、图8(b)所示。模态匹配之前，驱动模态已工作稳定，调谐电极上施加了固定调谐电压Vt，Vt=Vt1=4.5 V，虚拟科氏力为 0。模态匹配之后，调谐电压Vt稳定在5.7 V。由于科氏力来自于驱动模态振动速度，虚拟科氏力是科氏力的模拟，故虚拟科氏力与驱动模态输出也正交。而模态匹配后，虚拟科氏力产生的敏感输出会产生90°相位滞后，故驱动模态输出与敏感模态输出同相。所以，图8(b)符合模态匹配后的相位特征。模态匹配调节的过程如图8(c)所示，可以看出，虚拟科氏力输入后，模态匹配闭环立即启动，调谐电压从4.5 V快速上升并稳定到5.7 V，敏感模态输出也快速增大并稳定振荡。

图8 模态匹配实现

模态匹配过程中，虚拟科氏力作用在敏感模态的虚拟科氏输出Vd、相位差电压V(φs)和PI控制器输出的调谐电压Vt1的关系如图9所示。虚拟科氏力输入后，随着Vt1由0快速上升并稳定到1.2 V，V(φs)抖动一下被快速控制在0附近，系统快速达到模态匹配状态，Vd逐渐增加到最大值。可以看出，模态匹配控制环路可以实现对调谐电压的稳定控制，并且模态匹配后可以增大输入信号的响应，这意味着标度因子的增大。

3.3 模态匹配与科氏力反馈闭环检测

由于模态匹配时，陀螺的标度因子会增加，这意味着更小的输入角速度就可以产生同样的科氏输出，在更大的输入角速度时系统的线性度将变差。同时，敏感输出也更容易达到电路饱和状态。为了增加可检测角速度的范围，在模态匹配稳定后，启动科氏力反馈闭环，整个控制系统控制效果如图10所示。

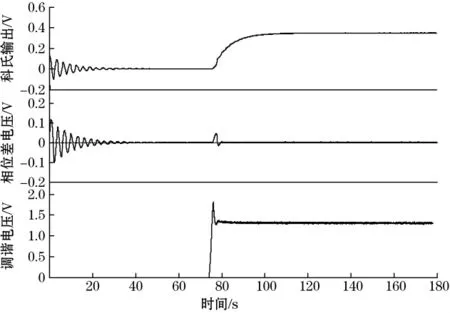
图9 科氏输出、相位差电压与频率调谐电压

模态匹配过程与图9类似，只是输入虚拟科氏力后延时了大约20 s才启动模态匹配控制，效果是一样的。启动科氏力反馈闭环控制后，科氏力反馈抑制了部分虚拟科氏力，敏感输出幅度变小，被稳定控制在－0.2 V，科氏力相位差与调谐电压保持不变。由图10可知，实验与仿真结果吻合，证明所设计的方法能在十六边形陀螺实现模态匹配与闭环检测。

图10 模态匹配与闭环检测控制效果

3.4 标度因子与零偏不稳定性

实验测得所用十六边形陀螺在模态不匹配(开环检测)时的标度因子为 13 mV/［(°)·s－1］，在模态匹配后，开环检测标度因子为 158 mV/［(°)·s－1］，闭环检测标度因子为 76 mV/［(°)·s－1］，如图11 所示(模态匹配时减去了其偏置)。

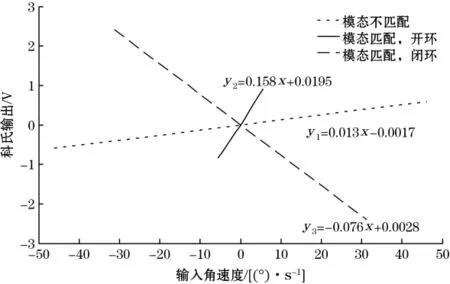
图11 系统标度因子

尽管模态不匹配时，陀螺的标度因子也不小，但是，高Q值陀螺受干扰后振动幅度较大、稳定时间较长。如图12所示，模态不匹配时，角速度输入后需要将近50 s才能稳定下来，而模态匹配能在几秒时间内稳定。

图12 模态不匹配时，科氏输出需要非常长的时间才能稳定

模态匹配时，本课题组的陀螺获得非常大的标度因子。但是，也正是标度因子较大，较小的角速度输入就会超出陀螺的线性范围。而陀螺敏感闭环检测通过科氏力反馈抑制了敏感模态的振动，通过反馈科氏力检测角速度，能承受较大的角速度输入。

如图13所示，通过Allan方差计算得到陀螺在模态不匹配以及模态匹配时开环检测、闭环检测的零偏不稳定性分别为 13.5、1.1、2.3°/h。

图13 系统零偏不稳定性

模态不匹配时(开环)陀螺性能及模态匹配时开环检测、闭环检测下陀螺性能比较如表2所示。

表2 研究使用的十六边形陀螺性能

根据表2的结果，相比于模态不匹配(开环)，模态匹配(不管是开环检测还是闭环检测)系统的零偏不稳定性都明显降低了，说明模态匹配可以在提高标度因子的同时降低零偏不稳定性，增加响应速度。而模态匹配时，与开环检测相比，由于闭环检测的标度因子降低了(降低了2.08倍)，由此带来了其零偏不稳定性的增加(增加了2.09倍)。

需要说明的是，表2中模态不匹配时，只测试了±46°/s以内的角速度输入。模态匹配闭环检测时的输入角速度范围受电路的限制，只能产生±2.5 V以内的反馈电压，而不是陀螺本身的限制，优化电路设计可能获得更大的角速度输入。

4 结束语

为了提高陀螺检测性能，设计了一种基于虚拟科氏力相位特性的硅MEMS十六边形陀螺自动模态匹配控制方法，通过施加虚拟科氏力到陀螺敏感模态的力反馈电极以激励敏感模态，根据敏感模态输出与虚拟科氏力之间的相位差来控制调谐电压，从而实现模态匹配。实验结果表明，无论开环还是闭环，自动模态匹配都可以增大陀螺的标度因子、改善零偏不稳定性以及响应速度。模态匹配时，开环检测可以获得较大的标度因子，而闭环检测可以测量更大的输入角速度。下一步的研究将集中在提高开环检测时的可输入角速度，闭环检测时的标度因子。