故障工况下有杆泵采油系统运行特性及示功图研究

吕孝孝, 王旱祥, 刘延鑫, 陈升山, 孙秉宇

(中国石油大学(华东)机电工程学院,山东青岛 266580)

有杆泵采油系统主要包括地面抽油机、井底抽油泵和起传递作用的抽油杆,其作为传统的机械采油方式,占油田生产方式的80%以上[1]。采油系统的运行特性与油田效益直接相关,因此国内外对此进行了大量的研究也取得了丰富的成果,Gibbs等[2]针对理想直井提出一维波动方程,对抽油杆振动以及柱塞位移的研究进入理论分析阶段,之后建立了考虑更多因素的改进模型[3-6]。但大都集中在对正常工况下采油系统运行特性的研究,对于故障工况下采油系统的运行特性研究较少。董世民等[7]将柱塞运动简化为正弦运动,建立了在气体影响和柱塞漏失条件下泵阀独立仿真模型,但未考虑固定阀和游动阀漏失的影响,且没有考虑漏失单独影响下的情况以及和抽油杆柱运动耦合的影响。綦耀光等[8]考虑泵阀动力学和水力摩阻建立了两相流时的泵阀特性模型。王宏博等[9]考虑地层瞬时流入特性建立了低产井的即供液不足时的仿真模型,Xing等[10]建立了考虑气体影响的直井抽油杆柱仿真模型,但均没有考虑杆管环空井液的压力波动的影响且无法对产液量进行预测。陈培毅等[11]采用最优控制理论建立直井故障工况地面示功图的获取方法,但依赖泵动力仪测取泵功图。另外,以地面示功图对有杆泵采油系统进行诊断是常用工况诊断方法[12-15]。但对于碳纤维抽油杆等新型抽油杆,其运行特性与钢制抽油杆不同,且由于应用时间较短,无充足的现场实测示功图,若用钢杆采油系统的示功图图库进行诊断则会降低诊断的准确性。针对这些问题,笔者建立正常工况、气体影响、漏失影响和供液不足等工况下的泵阀运行特性模型,与杆管液的动力学模型进行耦合,得到故障工况下的有杆泵采油系统的仿真模型。

1 杆管液耦合动力学模型

假设:①抽油杆和油管同心;②钢制抽油杆各向同性;③忽略地面电机转差率。

1.1 杆管液运动方程

抽油杆运动方程[10]为

(1)

式中,u为抽油杆单元节点位移,m;ρ为抽油杆材料密度,kg/m3;A为抽油杆截面面积,m2;g为自由落体加速度,m/s2;Frt为油管对单位长度抽油杆摩阻力,N;Frf为井液对单位长度抽油杆摩阻力,N;α为井斜角,(°);t为时间,s;s为抽油杆节点位置,m。

杆管环空井液运动方程为[10]

(2)

式中,ρf为井液密度,kg/m3;vf为杆管环空井液速度,m/s;Af为井液截面面积,m2;Ftf为井液对单位长度油管摩阻力,N。

连续方程为

(3)

井液的密度只是压力的函数,表示为

ρf=ρf0[1+Co(s)(pf-p0)].

(4)

式中,p0为标况下大气压,Pa;ρf0为标况下井液密度,kg/m3;Co为井液压缩系数,s2/m2。

当油管不锚定时,油管会随着抽油杆的振动而振动。

油管运动方程为[4]

(5)

式中,ut为油管单元节点位移,m;ρt为油管材料密度,kg/m3;At为油管截面面积,m2。

摩阻计算如下:

井液对抽油杆的摩阻力Frf为

(6)

井液对油管的摩阻力Ftf为

(7)

抽油杆与油管间的摩擦力Frt为

(8)

根据杆管同心假设和动量矩定理可得抽油杆和油管之间的法向压力Nn和副法向压力Nb。

(9)

(10)

式中,crf为井液与抽油杆之间的摩阻系数,N·s/m,包含接箍影响;ctf为井液与抽油杆之间的摩阻系数,N·s/m;f为抽油杆和油管之间的摩擦系数;I为抽油杆截面惯性矩,m4;T为井眼轨迹的挠率,rad/m;k为井眼轨迹曲率,m-1;φ为井斜角,(°)。

1.2 碳纤维抽油杆本构关系

碳纤维抽油杆为各向异性且非均匀材料,其拉伸模量和弯曲模量并不相同,在应用运动方程组(式(1)～(10))对其运动进行描述时,需对其力学参数拉伸刚度EA和弯曲刚度EI进行精确等效替换。碳纤维抽油杆截面如图1所示,包括碳纤维拉挤层、防止碳纤维拉挤层劈散的玻璃纤维包覆层和玻璃纤维拉挤层3层,其中玻璃纤维包覆层很薄可忽略不计。

图1 碳纤维复合材料抽油杆截面Fig.1 Section of carbon fiber composite sucker rod

利用混合定律可得碳纤维抽油杆的轴向等效拉伸刚度为

(11)

等效弯曲刚度为

(12)

式中，dCM和dGM分别为碳纤维拉挤层直径和玻璃纤维层外径，m;ECM和EGM分别为碳纤维和玻璃纤维拉挤层拉伸模量，Pa。

1.3 边界条件

1.3.1 上边界条件

抽油杆柱上端与悬点位移相同,油管头静止,井口井液的压力为油压。

(13)

式中,SA为抽油机悬点位移,m,在此游梁式抽油机悬点精确运行[16];po为油压,Pa。

1.3.2 变截面处连续条件

变截面处连续条件为

(14)

式中,Li+和Li-表示变截面处的下部和上部;Ei和Ei+1分别为第i级和第i+1级抽油杆弹性模量,Pa;Ai和Ai+1分别为第i级和第i+1级抽油杆截面面积,m2;pLi为变截面处井液压力,Pa;Afi和Afi+1分别为第i级和第i+1级井液截面面积,m2。

在此假设油管柱规格相同,无变截面连续条件;若油管规格不相同,则油管变截面连续条件与抽油杆类似。

1.3.3 下边界条件

泵处抽油杆柱即柱塞,油管即泵筒和杆管环空井液相互作用如图2所示。

图2 泵处运动受力分析Fig.2 Force and motion analysis at pump

抽油杆柱底端即柱塞受力平衡,表示为

(15)

式中,Ern为最后一级抽油杆弹性模量,Pa;Arn为最后一级抽油杆截面面积,m2;p*为抽油泵泵筒内压力,Pa;Lp为泵挂深度即抽油杆柱的总长度,m;Ap为柱塞截面面积,m2;Fc为泵筒与柱塞之间的摩擦力,N;λ为摩擦力符号,柱塞相对泵筒向上,λ=1;柱塞相对泵筒向下,λ=-1;柱塞相对泵筒静止,λ=0。

油管柱底部即泵筒受力平衡,表示为

psAto-λFc.

(16)

式中,Ati为油管截面内圆面积,m2;Ato为油管截面外圆面积,m2。

游动阀开启时,泵内压力为排出压力与排出压降之和。固定阀开启时,泵内压力为泵吸入口压力与吸入压力之差。固定阀和游动阀均处于关闭状态时,柱塞位移、泵筒位移与泵筒压力之间关系记为泵阀运行特性函数Φ,即

Φ[u(Lp,t),ut(Lp,t),p*(t)]=0.

(17)

pf(Lp,t)用前一时刻代替当成已知量,联立式(9)～式(11),即可求得u(Lp,t)、ut(Lp,t)和p*(t)。

杆管环空底部井液流速。根据井液流量守恒可得杆管环空底部井液流速与柱塞速度vp和泵筒速度vb的关系,记为Ψ。

vf(Lp,t)=Ψ[vp(t),vb(t)],

(18)

其中

vp(t)=∂u(Lp,t)/∂t,vb(t)=∂ut(Lp,t)/∂t.

式中,vp和vb分别为柱塞、泵筒运动速度,m/s。

1.4 模型求解

1.4.1 初始条件

以下冲程结束时刻为初始时刻,固定阀和游动阀均关闭,泵筒内压力为排出压力。

(19)

式中,u0为泵筒压力为排出压力pd时杆柱的悬垂位移,m;pfs为杆管环空井液静止分布压力,Pa。

1.4.2 求解方法

用有限差分方法[17]对所建模型进行求解,求解流程如图3所示,图中,fs和fd分别表示固定阀和游动阀的状态,值为0表示阀关闭,值为1表示阀开启;ps为泵吸入口压力,Pa,Δps为井液过固定阀压降,Pa;Δpd为井液过游动阀压降,Pa;tend为仿真时长,s;tend一般为为3～4个运动周期,当运动稳定时输出最后一个周期的结果即为最终仿真结果。

2 故障工况泵阀特性函数

不同泵工况下泵阀特性函数Φ和井液底端流速函数Ψ均有所不同。

2.1 正常工况

2.1.1 泵阀运行特性函数Φ

由于泵筒内体积较小,泵筒内井液的压缩性可忽略不计,则泵阀特性函数Φ为

Φ=vp(t)-vb(t).

(20)

2.1.2 杆管环空井液底端流速函数Ψ

杆管环空井液底端流速函数Ψ为

(21)

式中,Afn为最后一级杆管环空井液的截面面积,m2。

2.2 气体影响

泵筒内含气变化如图4所示。假设:油气水混合液均匀进泵和排出;不考虑阀球的自重;气液两相流中液相不可压缩,仅考虑气体的可压缩性,气体的压缩和膨胀按多变过程进行。

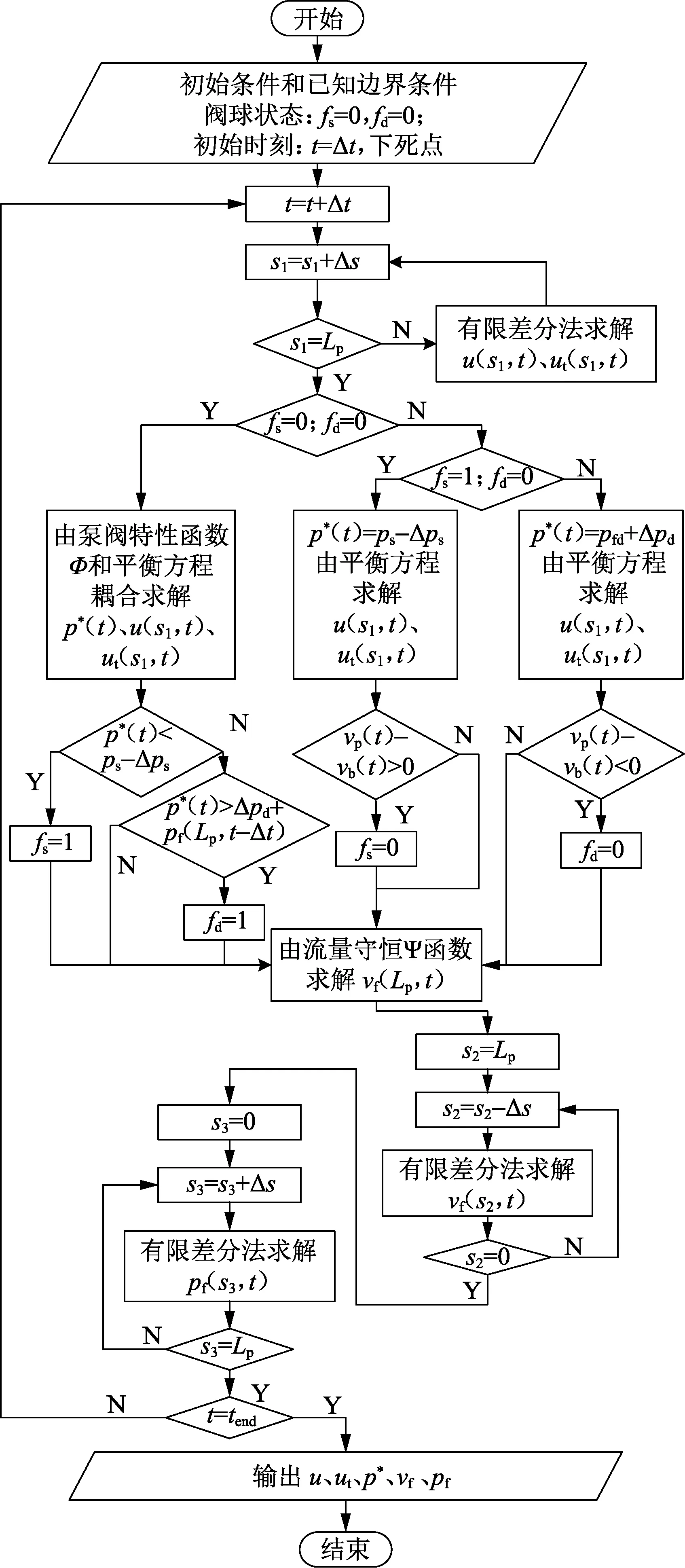
图3 耦合模型求解流程Fig.3 Solving process of coupled model

由气体状态方程可得

(22)

式中,sg为泵筒内气柱高度,m;κ为气体多变过程系数,一般κ=1.1。

泵筒内气柱高度变化为

(23)

其中

式中,R和Rd分别为泵吸入口和排出口气液比;Rs为泵入口天然气在原油中的溶解度;Rp为地面气油比;fw为含水率;p0为标准大气压力,Pa;rg为天然气相对密度;ro为脱气原油相对密度;Tp为泵温度,K。

图4 气体影响下泵阀特性Fig.4 Pump valve characteristics under gas effect

式(16)为一阶微分方程,求解时需要初始条件即柱塞在下死点时泵筒内气体高度为

(24)

式中,Ls为防冲距,m。

联立式(22)～(24)形成气体影响下泵阀运行特性函数Φ。

气体影响工况下的井液底端流速函数Ψ与正常工况相同。

2.3 泵阀漏失影响

如图5所示,泵处漏失有柱塞漏失、固定阀漏失和游动阀漏失3处。阀漏失的影响是由于阀座、阀球磨损或阀座有异物阻碍引起的阀球与阀座无法密封。

2.3.1 泵阀运行特性函数

设流入泵筒内为正,则柱塞间隙漏失[19]为

qp(t)=ξp[pf(Lp,t)-p*(t)],

(25)

其中

ξp=πDpδ3/(12μlp).

式中,qp为柱塞漏失速度,m3/s;ξp为柱塞漏失常数;Dp为柱塞直径,m;δ为柱塞与泵筒之间的间隙,m;μ为泵内井液黏度,Pa·s;lp为柱塞长度,m。

固定阀和游动阀两端的漏失量为

qs(t)=-ζsξp[p*(t)-ps]es,

(26)

qd(t)=ζdξp[pf(Lp,t)-p*(t)]ed.

(27)

式中,qs和qd分别为固定阀和游动阀的漏失速度,m3/s;ζs和ζd分别为固定阀和游动阀的漏失系数;es和ed为压力差指数,静止且间隙为同心圆柱时为1。

图5 漏失影响下泵阀特性Fig.5 Pump valve characteristics under leakage effect

由于阀漏失间隙不规则,且柱塞运动对阀漏失的影响,如上下冲程由于柱塞的速度与漏失方向不同,上冲程会加快漏失,下冲程会减缓漏失,因此压力差的指数会由所不同。

由柱塞让出的空间与井液漏失体积相等,表示为

(vb-vp)Ap=qs+qd+qp.

(28)

联立式(25)～(28)可得漏失影响下泵阀运行特性函数Φ。

2.3.2 杆管环空井液底端流速函数

由于有井液漏失,因此杆管环空井液底端流速函数与正常工况不同。

vf(Lp,t)=

(29)

2.4 供液不足

供液充足时,沉没度较大,动液面轻微波动引起的泵吸入口压力变化对系统性能的影响较小,一般可认为是不变量。如图6所示,供液不足时,泵同时会形成部分真空,此时动液面波动对井液进入泵筒内的流量影响十分严重,因此需考虑瞬时的动液面高度和泵入口压力。

2.4.1 瞬时吸入口压力

采用Vogel模型[20]计算地层流入泵筒内的瞬时流量,表示为

(30)

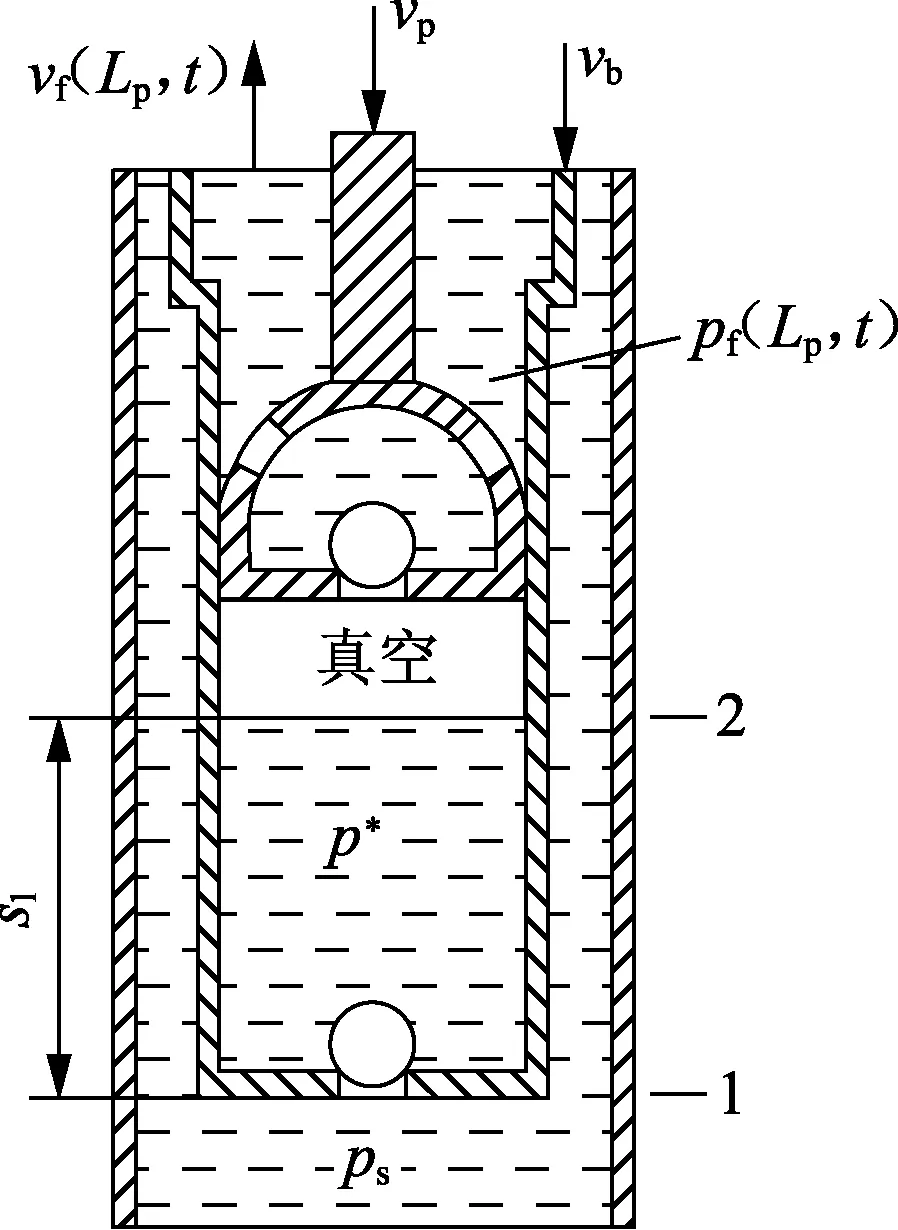
图6 供液不足时泵阀特性Fig.6 Pump valve characteristics with deficient-liquid supply

动液面高度瞬时变化为

(31)

泵吸入口瞬时压力为

ps=pc+ρf1g(Lp-Ld).

(32)

瞬时流压为

psf=pc+ρf2g(Lo-Ld).

(33)

进入泵筒的瞬时流量为

pout=v2Ap.

(34)

式中,qin为地层瞬时流入井筒流量,m3/d;qmax为油井最大产量,m3/d;pr为油井静压,Pa;psf为井底瞬时流压,Pa;Ld为动液面高度,m;qout为进入泵筒内的瞬时流量,m3/s;Act为油套环空截面面积,m2;pc为套压,Pa;ρf1为动液面到泵入口井液平均密度,kg/m3;ρf2为动液面到井底井液平均密度,kg/m3;Lo为油藏中深,m;v2为泵筒井液液面上升速度,m/s。

2.4.2 泵阀运行特性函数

加载过程与正常工况相同。固定阀打开,上冲程开始,对1、2两面,由伯努利方程得

(35)

泵筒内井液高度与速度的关系为

dsl/dt=v2.

(36)

连续方程为

Aciv1=Apv2.

(37)

式中,p2为柱塞底部的井液压力,Pa;sl为泵筒内井液高度,m;ρfs为泵吸入口井液密度,kg/m3。

上冲程初始,柱塞速度较小,且泵筒内液柱高度较低,井液有充足的能量克服过阀阻力进入泵筒,泵筒内液面上升的流速与柱塞相对泵筒的速度相同。

v2=vb-vp.

(38)

联立式(30)～(38)可求得柱塞底部井液瞬时压力p2;当p2≤0 时,泵筒内开始形成真空,记此时的时刻为tv。抽真空后泵内井液的流速[21]为

(39)

式中,Kv为阀流量系数。

当柱塞相对泵筒下行碰到液面前,游动阀不开启;当v2>0时一直有井液进入泵筒,若再此之前,v2=0,则说明泵筒内的井液已经达到可达到的最高高度。当柱塞碰到液面后,柱塞相对泵筒静止,开始卸载,过程与正常工况相同,判断条件为

(40)

供液不足工况的泵阀运行特性函数与正常工况相同,由于吸入压力较小,假设吸液和排液过程中ps=0,则上冲程与下冲程的受力也与正常工况相同,只是固定阀关闭的条件由柱塞相对泵筒下行变为柱塞接触到泵筒液面;在接触到泵筒液面后会产生较大的冲击载荷。

供液不足度为

(41)

式中,DE为供液不足度;Sp为柱塞冲程,m;Spv为柱塞有效排液冲程,m。

供液不足工况的杆管环空井液底端流速函数与正常工况相同。

3 实例井验证及分析

针对实际生产井,利用所建故障工况仿真模型进行计算。

产液量预测为

(42)

式中,Qp为系统采油预测产液量,m3/d;Afn为井口井液截面面积,m2;Bl为井液压缩系数;N为冲次,min-1。

3.1 碳纤维钢混合抽油杆采油系统实例仿真

以DXY13N14井2017年2月20日生产井况为例,油井基础参数为:泵挂1 500 m,沉没度300 m,泵径63 mm,使用冲程2.9 m,冲次3.9/min,杆柱组合碳杆22 mm×1 000 m+钢杆25 mm×500 m,73 mm平式油管,不锚定。仿真结果如图7所示。

图7 正常工况地面示功图对比及仿真泵功图Fig.7 Comparison of ground indicator diagrams and simulated pump diagrams under normal conditions

由图7可知,仿真泵功图的加载和卸载线不是垂直线,表明油管不锚定,柱塞上行和下行时载荷并不是定值,是由柱塞上端井液即杆管环空下端井液压力的波动导致。碳纤维抽油杆采油系统仿真结果与实测结果具有良好的一致性,且预测日液量为26.47 m3,实际日液量为25.6 m3,误差为3.4%,表明所建模型可对碳纤维抽油杆等新型抽油杆正常工况下的有杆泵采油系统进行准确仿真。

油井基础参数和生产参数:泵挂深度1 800 m,沉没度400 m,泵径56 mm,冲程4.8 m,冲次3/min,73 mm平式油管,锚定。钢抽油杆柱组合25 mm钢杆×600 m+22 mm钢杆×1 200 m;碳纤维钢混合抽油杆柱组合22 mm碳纤维杆×1 200 m+25 mm钢杆×600 m;地面示功图仿真结果如图8所示。正常工况下采油系统地面示功图分4个阶段,加载段AB,柱塞上行段BC,卸载段CD和柱塞下行段DA。相同工作条件下,碳纤维钢混合杆柱采油系统相比于钢制抽油杆由于杆柱弹性较大,因此加载和卸载段较长;杆柱的固有频率较低,因此柱塞上行和下行段谐波个数较少;另外,由于碳纤维抽油杆和钢杆弹性相差较大,振动比较平缓,因此谐波比较平滑。

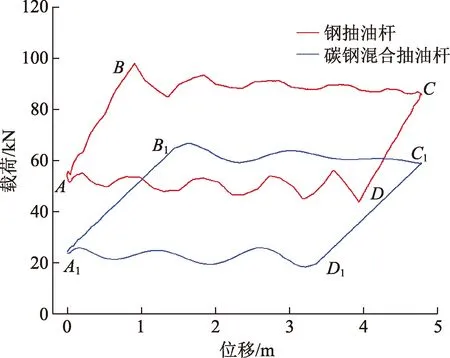
图8 正常工况不同抽油杆柱地面示功图对比Fig.8 Comparison of ground indicator diagrams of different sucker rod strings under normal conditions

3.2 故障井实例仿真

针对不同工况的油井,对模型设置不同的故障参数组合[R,ζd,ζs,DE],其中DE由沉没度控制,计算好后,再利用文中式(41)进行计算;通过遗传优化算法得到一组故障参数组合,使得仿真地面示功图与实测示功图误差最小,利用该组故障参数对故障井进行仿真分析。每种故障对2口实例井进行仿真分析,油井生产参数、得出的故障参数及日液量等如表1所示,仿真示功图如图9～12所示。

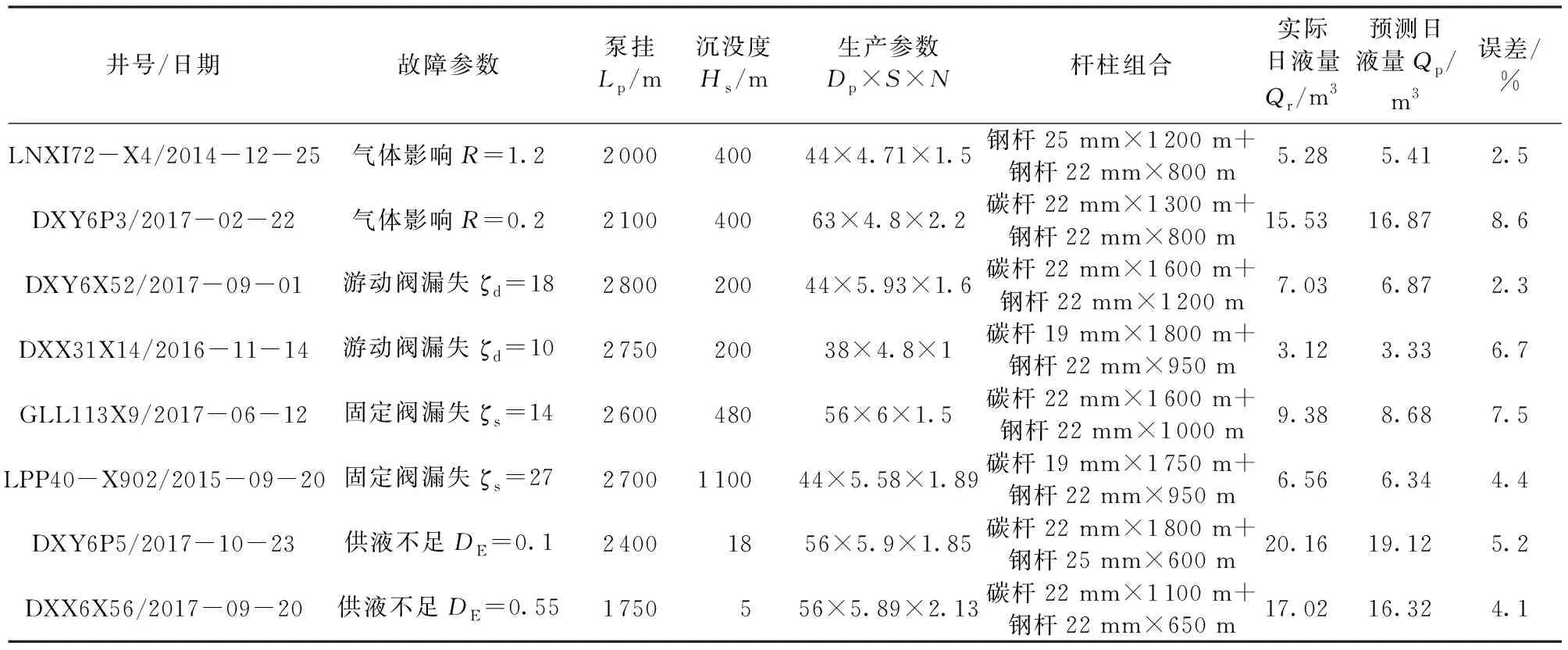
表1 实际生产井基础参数及产液量预测

由表1可知各种工况下采油系统的产液量预测误差最低为2.3%,最高为8.6%,平均误差为5.6%,满足现场预测要求,表明所建故障工况仿真模型可有效地对采油系统产液量进行预测。

仿真地面示功图与实测地面示功图均有良好的一致性。说明仿真结果可真实地反应悬点载荷和柱塞运动规律,验证了所建仿真模型的准确性和适应性。

图9 气体影响地面示功图对比及仿真泵功图Fig.9 Comparison of ground indicator diagrams and simulated pump diagrams under gas influence condition

图10 游动阀漏失地面示功图对比及仿真泵功图Fig.10 Comparison of ground indicator diagrams and simulated pump diagrams under travelling valve leakage condition

如图9所示,由于气体影响,加载和卸载均滞后,所以加载线和卸载线均延长,但由于卸载时比加载时泵筒内的含气较多,因此卸载线比加载线长。由于气体体积变化引起的压力变化非线性,因此加载线和卸载线并不是直线,而是弧线。加载气体膨胀,载荷越来越平缓,导致加载线斜率越来越小,因此加载完成时振动载荷减小;卸载气体压缩,载荷越来越剧烈,卸载线斜率绝对值越来越大,因此加载完成时振动载荷增大。由图10可知,由于游动阀漏失使得固定阀打开滞后,游动阀打开提前,导致悬点加载滞后,卸载提前,因此地面示功图加载线斜率减小、长度增加,卸载线斜率绝对值增加长度变短。如图11所示,固定阀漏失与游动阀漏失影响相反,地面示功图加载线斜率增加、长度变短,卸载线斜率绝对值减小、长度增加。如图12所示,供液不足对加载段和柱塞上行段影响不大,下冲程时,首先摩阻力换向卸载小部分载荷,然后柱塞下行碰到泵筒内的液面时开始卸载,卸载完成后有较大的振动载荷。

综上故障仿真模型可对故障工况下地面示功图的特征进行准确仿真,可对故障进行量化分析及日液量预测;同时利用故障仿真模型,设置不同的油井参数和生产参数,即可得到新型抽油杆柱采油系统的故障示功图图库。新型抽油杆在不同工况下的泵阀运行特性虽然一致,但由于杆柱刚度不同,地面示功图的加载线、卸载线长度和斜率不同加上谐波变化的影响,使得地面示功图特征有所区别。在使用神经网络等智能诊断方法对采油系统进行诊断时,会使得分类的阈值有所差异,因此需要用其对应抽油杆类型的故障示功图图库进行训练,才能对故障进行准确诊断。

图11 固定阀漏失地面示功图对比及仿真泵功图Fig.11 Comparison of ground indicator diagrams and simulated pump diagrams under standing valve leakage condition

图12 供液不足地面示功图对比及仿真泵功图Fig.12 Comparison of ground indicator diagrams and simulated pump diagrams under liquid insufficient condition

4 结 论

(1)碳纤维混合杆柱相对于钢杆采油系统示功图载荷绝对值较小,加载和卸载线较长,谐波个数较少且平滑。

(2)针对故障工况实际生产井,对其运行特性进行仿真,仿真得出的地面示功图与实测地面示功图具有良好的一致性。同时根据故障仿真模型建立了产液量预测方法,预测结果与实际产液量的平均误差低于6%,验证了所建故障仿真模型满足现场使用的精度要求。

(3)通过故障仿真模型可得到新型抽油杆采油系统的故障示功图图库,为获取故障示功图图库提供了新方法。