基于无网格法的浮体与波浪相互作用模拟与试验验证

李增亮, 王乐峰, 董祥伟, 杜明超, 荆正军, 王雨婷

(1.中国石油大学(华东)机电工程学院,山东青岛 266580; 2.中国石油大学(华东)石油工业训练中心,山东青岛 266580;3.中国石油海洋工程有限公司青岛分公司，山东青岛 266555)

波浪与浮体的相互作用现象广泛存在于海洋能源领域,例如海洋平台在波浪中的运动响应[1],浮子式波浪能发电装置的波浪能转换过程[2]等。近年来,国内外在波浪能转换方面做了很多研究,世界上第一个关于波浪能发电技术的专利诞生于1799年[3],日本于20世纪80年代初建成了总装机高达1 250 kW的波浪能转换装置[4],中国的广州能源研究所于1984年研制成功的波浪能转换装置已在沿海海域大规模投入使用[5]。波浪与浮体的相互作用是典型的流固耦合问题,同时涉及自由表面流动、浮体结构物的运动等。学者们采用数值模拟手段对波浪的水动力学特性进行了研究。王永学[6]利用VOF方法建立无反射造波数值波浪水槽；董志等[7]利用VOF方法建立数值波浪水槽并对造波消波方法进行研究；胡杭辉等[8]进行了基于Fluent的二维非线性数值波浪水槽构造及验证的研究；臧志鹏等[9]利用试验装置研究波浪发电系统振荡浮体的运动特性。但是,当涉及波浪与浮体相互作用的数值模拟时,由于网格特性的限制和浮体的拉格朗日运动特性,传统的基于欧拉方法(如有限体积法)的数值模拟手段并不适用于该类问题的求解。近年来,无网格粒子法逐渐兴起,光滑粒子动力学方法(SPH)是最具代表性的方法之一[10]。倪兴也等[11]采用SPH方法建立二维数值波浪水槽,模拟了推板造波过程;常江[12]采用SPH方法建立三维数值波浪水槽,得到的波浪运动特性与试验结果吻合较好。作为一种粒子法,SPH方法的主要优点在于不需要画网格,在处理自由表面流动与固体的流固耦合过程中较有优势。笔者将SPH方法应用于波浪与浮体相互作用的数值仿真研究,借助开源程序DualSPHysics建立三维数值波浪水槽,并搭建造波水槽试验台,通过试验对比验证数值模型的适用性。

1 数值方法及模型

1.1 SPH方法原理

光滑粒子动力学方法(smoothed particle hydrodynamics,SPH)是一种拉格朗日无网格法。与有限体积等网格法不同,SPH方法利用一组粒子离散连续体计算域。在SPH流体力学仿真中,根据周围颗粒物的物理性质,Navier Stokes方程在每个粒子处进行局部积分,积分域内包含粒子的集合是由基于距离的函数来确定的。例如,对于二维问题,该积分域是以相关粒子为圆心的圆形区域;对于三维问题,积分域是以相关粒子为球心的球形区域。在SPH方法中,物理量赋值在每一个粒子上,在每一个时间步粒子各物理量都会被重新计算,然后粒子根据这些重新计算的数据产生新的位移。因此,SPH方法是一种拉格朗日数值模拟方法。

假定一任意场函数F(r),其可以通过核函数近似写成积分表达形式:

(1)

式中,W(r-r′,h)为核函数;h为核函数的光滑长度。

式(1)又称为场函数F的核近似表达。由于计算域被离散成一系列粒子,F函数的粒子近似可写成:

(2)

式中,下标a代表当前SPH粒子;下标b代表粒子a的邻域粒子(b粒子位于a粒子的支持域内);mb为粒子b的质量;ρb为粒子b的密度。

1.2 核函数选择

在SPH方法中,存在多种形式的核函数,核函数的选取将直接影响数值计算的精度。DualSPHysics程序中内置了2种核函数,分别为五次样条核函数和三次样条核函数。经过对比发现,在其他条件不变的情况下,五次样条核函数得到的波浪流场的压力分布结果要优于三次样条核函数,因此选取了五次样条核函数[13]:

(3)

其中

式中,q为无量纲距离;r为任意两粒子a与b之间的实际距离;h为光滑长度。

对于任意粒子a,其领域粒子是由粒子a的光滑半径决定的,光滑半径又与光滑长度h有关。对于式(3),当q大于2时核函数的值为0;只有q小于2时,核函数才是有效的,这也说明SPH核函数是紧致的。

1.3 流体控制方程

流体运动由流体控制方程描述,即纳维斯托克斯方程(N-S),包括质量守恒方程和动量守恒方程。质量守恒方程为

(4)

式中,ρ为流体密度,kg/m3;v为流体速度,m/s。

在SPH中,方程(4)可以写成粒子离散形式,表示为

(5)

其中

vab=va-vb.

式中,mb为粒子b质量,kg;vab为粒子速度,m/s;Wab为a和b粒子之间核函数值。

图1 光滑核函数及其导数图像Fig.1 Smooth kernel functions and derivatives of smooth kernel functions

动量守恒方程为

(6)

式中,t为时间,s;p为压力,Pa;g为自由落体加速度,m/s2;Γ为耗散项。

采用粒子近似方法,方程(6)可以写成SPH离散形式:

(7)

式中,pa和pb分别为粒子a、b处压力;ρa和ρb分别为粒子a、b处密度。

Πab为人工黏性力[14],其作用是消除数值计算时计算域中的非物理震荡。人工黏性力为

(8)

其中

式中,v为粒子速度,m/s;α为常数,在自由表面流动模拟中一般取0.01[15];Cab为声速的平均值,即a粒子和b粒子代表的流体的声速平均(流体为水介质,因此a粒子和b粒子的声速相同)。

在本文模拟中,流体被当作弱可压缩的,采用状态方程来计算流体压力。状态方程表达为流体压力和密度之间的关系式[16]:

(9)

其中

式中,ρ0为参考密度,取为1 000 kg/m3;c0为流体声速。

水的物理声速为1 500 m/s,但在实际模拟过程中,由于流体是弱可压缩性的,一般可通过给定声速一个较低值,只要保证密度的波动低于1%即可;实际的声速可计算为c=10vmax,其中vmax为计算域中流体的最大速度。

1.4 浮体受力及运动方程

浮体与流体相互作用过程中,将浮体考虑为刚体,并也离散成SPH粒子。根据积分步骤,可以计算出每一边界粒子k受到的周围流体粒子所给出的力fk:

(10)

mkfka=-mafak.

(11)

式中,fka为流体粒子a作用在边界粒子k上的作用力(a粒子位于k粒子的支持域之内),N;fak为边界粒子k作用在流体粒子a上的反作用力,N;ma和mk分别为流体粒子和边界粒子的质量,kg。

图2为浮体的边界条件。

图2 浮体的边界条件Fig.2 Boundary conditions for floating bodies

对于运动的刚体,可通过刚体的运动方程求出,包括平动方程和转动方程:

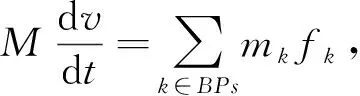
(12)

(13)

式中,M为刚体质量,kg;I为惯性矩,m4;Ω为角速度,rad/s;R0代表质心。

对式(12)、(13)进行积分即可得到刚体在某时间的速度和角速度。由于刚体的SPH粒子是附着在刚体上的,可以认为是质点,则每一边界粒子的速度uk为

uk=v+Ω(rk-R0).

(14)

1.5 数值模型

数值模拟是基于DualSPHysics完成的。DualSPHysics是一款开源的SPH程序,由c++语言编写,借助于FreeCAD前处理接口程序可以实现在Windows平台对流体力学问题进行数值建模和SPH模拟。依据实验室内波浪水槽的实际尺寸,建立波浪和浮体相互作用的数值模型,如图3所示。模型包含造波板、浮体、水、消波板及水槽。其中造波板、浮体、消波板及水槽壁面被处理为刚性边界。给定造波板一定的运动规律,推挤流体产生波浪运动行为。浮体被建模为可以自由运动的刚体,浮体与水的流固耦合作用由动态边界法(dynamic boundary)实现。图4为计算域示意图。计算域离散为一系列初始均匀分布的SPH粒子,粒子间距取值为8 mm。

图3 三维数值模型Fig.3 Three-dimensional numerical model

图4 离散后的三维数值模型Fig.4 Discrete three-dimensional numerical model

DualSPHysics中内置了多种时间积分格式,选用辛格式(symplectic scheme)。在第一阶段,其位移和密度可表示为

(15)

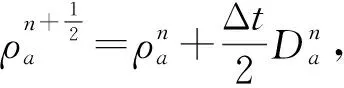
(16)

(17)

其中

(18)

(19)

(20)

仿真结果以数据表的形式输出,借助于第三方后处理软件Paraview完成结果的可视化。仿真过程中设置输出数据频率为每0.01 s输出一次,仿真的总物理时间为25 s。

造波采用推板式造波,水槽右侧采用斜坡式消波。水槽整体长度为3 m,高度为45 cm,宽度为50 cm;造波板宽度为492 mm,高度为400 mm,厚度为1.4 mm,造波板与水槽底部和水槽两侧的距离均为4 mm;浮体距离水槽左端80 cm且距离水槽两个侧面的距离相等,使得浮体处于有效工作区域。

为了研究浮体形状的影响,选取扁平型、球型和圆柱型3种浮体。首先研究圆柱型浮体,圆柱半径为50 mm,高度分别为30、50和70 mm,如图5所示;球型浮体模型,半径为45.428 mm;扁平型的浮体由两个球缺叠加在一起,高度为50 mm,球缺半径为108.33 mm;3种浮体如图6所示。浮体材料的密度设置为600 kg/m3,仿真过程中粒子间距为8 mm,水深100 mm。

图5 不同高度圆柱型浮体Fig.5 Cylindrical floater with different heights

图6 不同形状浮体外观Fig.6 Floater of different shapes

1.6 数值模型验证

根据已建立好的数值模型进行造波模拟。波形采用二阶斯托克斯波,表述为

(21)

式中,S0为造波板行程,m;ω为角速度,rad/s;δ为初相,rad。

(22)

其中

k=2π/L,

式中,H为波高,m;d为水深,m;L为波长,m。

二阶斯托克斯波为

e(t)=e1(t)+e2(t).

(23)

设置波高0.03 m、周期1 s、水深0.1 m。图7为不同时刻的波形图,图8为采用SPH方法模拟得到的波形与理论解对比。图8中SPH模拟得到的波形与理论解吻合较好,说明所建立的SPH模型能够有效预测推板造波水槽中波浪的自由表面流动特性。

图7 不同时刻波形Fig.7 Different instants of simulation with regular waves

图8 SPH和理论解波形对比Fig.8 Comparison of SPH and theoretical wave surface elevation

2 波浪水槽试验

2.1 试验装置和方案

搭建造波水槽试验台如图9所示。利用该试验装置进行波浪与浮体相互作用试验,将试验结果与仿真结果进行对比。试验台由造波机构和水槽两部分组成。造波机构包括电源、伺服电机控制器、伺服电机驱动器、750 W伺服电机、联轴器、丝杠导轨、造波板,如图10所示。水槽包括浮体、消波板、玻璃容器和支架,如图11所示。造波机构的工作原理为:伺服电机控制器控制电机旋转,丝杠导轨将电机的旋转运动转变为造波板的往复直线运动,造波板推挤流体产生波浪。水槽用透明玻璃制成,用高速摄像机记录浮体在波浪中的运动过程。后续通过图像处理,记录浮体的位置,通过描点的方式绘出浮体的运动轨迹,从而将试验数据与仿真数据进行对比。

图9 波浪水槽试验台Fig.9 Wave-making experimental device

图10 造波机构示意图Fig.10 Sketch map of wave making mechanism

图11 水槽部分示意图Fig.11 Sketch map of flume part

造波板的运动速度与电机的转速关系为

v′=kn.

(24)

式中,v′为造波板的运动速度,mm/min;n为电机转速,r/min;k为丝杠导程,本装置中k为4 mm。

2.2 水槽中浮体运动试验及仿真

图12为浮体初始时刻在流体中保持静止时的位置。根据阿基米德浮力定律可算出浮体在液体中静止时的吃水深度。

Ff=ρlgVd.

(25)

式中,Ff为浮体受到的浮力,N;ρl为液体密度,此处为水的密度,1 000 kg/m3;Vd为浮体排开液体的体积,m3。

图12 浮体在液面中静止时试验与仿真对比Fig.12 Comparison of experiment and simulation of floater at rest in liquid surface

图13为不同时刻试验与仿真对比。造波板运动规律如表1所示。为了保证仿真与试验条件一致,仿真过程中造波板运动规律与试验相同。

图13 仿真与试验不同时刻对比Fig.13 Comparison of simulation and experiment at different time

表1 试验与仿真过程造波板运动规律(部分数据)
Table1Motionlawofwave-makingplateinexperimentsandsimulations(some data)

序号速度/(m·s-1)时间/s行程/m 10.16660.360.06 2-0.16660.360.06 30.16660.360.06 4-0.16660.360.06 ………… 350.16660.360.06 36-0.16660.360.06

图14为水平方向和竖直方向浮体位置随时间的变化规律。由图14可知,若忽略装置造波板刚性不足的影响以及试验后处理过程中对浮体位置进行测量时误差的影响,试验与仿真结果基本一致,可认为采用本文中的仿真方法能够有效预测浮体在波浪环境下的运动规律,进而可以通过仿真来研究其他因素对波浪与浮体相互作用产生的影响。

图14 浮体水平及竖直方向随时间运动规律试验与仿真对比Fig.14 Comparison of experiment and simulation on law of horizontal and vertical motion of floating body with time

3 浮体在波浪水槽中的运动

3.1 浮体形状影响

仿真过程中为了保证各个浮体只有形状的区别,浮体的密度、体积均相同,波浪参数相同。

仿真过程中造波板的运动规律如表2所示,图15为不同形状的浮体在水平和竖直方向浮体位置随时间运动规律。

表2 仿真过程造波板运动规律(部分数据)

通过观察图15可以看出,水平方向,浮体沿着波浪方向不断前进,初始位置相同,初期位移曲线基本吻合,后期不同形状浮体的位移之差逐渐加大,扁平型在水平方向产生的位移最大,圆柱型次之,球型最小;竖直方向,初始位置相同,不同形状的浮体振幅基本相同,后期扁平型浮体相对于其他两种浮体纵坐标较高,圆柱型和球型两种浮体曲线基本吻合。说明浮体的形状对波浪与浮体相互作用影响较大,特别是在水平方向对浮体的运动规律有较大影响。

图15 不同形状浮体水平及竖直方向随时间运动规律Fig.15 Comparison of horizontal and vertical motion of floater with different shapes with time

图16为浮体横摇和纵摇随时间变化规律。其方向如图17所示。横摇与纵摇的大小体现出浮体摇晃的程度,在浮子式波浪能发电中,应尽量减小横摇与纵摇,降低横摇与纵摇对浮子式波浪能发电装置的影响。由图16可以看出,球型的摇晃角度最大,扁平型和圆柱型的接近。从图13可以直观地看出,随着波峰与波谷交替变换,浮体必然会产生纵摇。由图16可以看出,由于波浪传播方向的影响,扁平型和圆柱型纵摇的角度要远大于横摇的。

图16 不同形状浮体横摇及纵摇随时间变化规律Fig.16 Variation of rolling and pitching of floater with different shapes with time

图17 横摇与纵摇所表示的方向Fig.17 Rolling and pitching that direction

3.2 浮体尺寸影响

图18表示不同高度圆柱体浮体在16 s时刻水平方向发生的位移和水平方向受到的力。由于浮体高度逐渐增加,浮体质量会逐渐增大,浮体所受到的阻力会逐渐增大。由图18可以看出,随着浮体高度增加,浮体在水平方向位移逐渐减小,受到的力逐渐增大。图19为浮体随着高度增加发生倾斜现象。

图18 不同高度圆柱体浮体的位移与受力Fig.18 Displacement and force of cylindrical floater with different heights

图19 不同高度圆柱型浮体产生倾斜现象Fig.19 Inclination of cylindrical floater at different heights

由图19可知,高度越高,倾斜角度越大。浮子式波浪能发电装置中,浮体倾斜产生的扭矩对于发电装置非常不利,因此在发电装置中应该尽可能避免浮体发生倾斜现象,在设计浮体参数时应使浮体在波浪中避免发生倾斜现象。

3.3 浮体密度影响

图20为不同密度浮体在一个波峰经过浮体时的越浪现象对比。由图20可知,当波峰逐渐向浮体靠近时,浮体左侧被迫升高,右侧降低;当波峰达到浮体时,由于受到浮体的阻碍,使波浪质点上升,对于密度较大的浮体,其不能立即跟随波峰升高,从而导致波浪越过浮体,发生越浪现象。密度为600 kg/m3的浮体几乎不会产生越浪现象,而随着密度增加越浪现象越来越明显。密度为800 kg/m3的浮体即能观察到越浪现象,密度为900 kg/m3的浮体越浪效果更加明显。图21为有无越浪现象对比,图中左侧为密度为600 kg/m3的浮体,无越浪现象,右侧为密度为900 kg/m3的浮体,有明显的越浪现象。

图20 不同密度浮体越浪效果对比Fig.20 Comparison of overtopping effects of floater with different densities

图21 有无越浪现象对比Fig.21 Comparison of overtopping phenomenon and non-overtopping phenomenon

4 结 论

(1)相比于欧拉网格法,无网格SPH方法的建模流程更便捷,采用粒子直接填充流体计算域,流固耦合过程不受限于网格拓扑关系,更适应复杂几何形状的计算域,适用于浮体的大位移运动模拟。

(2)通过波浪理论验证了SPH模型对波浪运动波形模拟的正确性。在此基础上进一步模拟了浮体与波浪作用过程,得到的浮体位移-时间关系与试验数据吻合较好。同时,捕捉到了越浪、波浪作用下的浮体侧倾等现象,展现了无网格SPH方法在自由表面流动和浮体相互作用模拟中的优势。

(3)不同形状的浮体在波浪中的运动规律具有明显差别,相同形状的浮体不同的尺寸参数、密度对浮体的运动也会产生较大影响。