基于复模态法的深水钻井隔水管反冲响应力学特性

王宴滨, 高德利

(1.中国石油大学(北京)石油工程教育部重点实验室,北京 102249;2.中国石油大学(北京)油气资源与探测国家重点实验室,北京 102249)

在深水钻井某些工况下须紧急断开隔水管底部总成(low marine riser package, LMRP)和防喷器(blow-out preventer, BOP)的连接,LMRP和BOP一旦紧急解脱,隔水管会带动解脱后的LMRP作轴向振动,这就是隔水管的反冲响应。防止解脱后的BOP与LMRP发生碰撞,对于确保深水钻井安全具有重要意义。Puccio等[1]提出了影响紧急解脱后隔水管反冲响应速度和位移的关键参数。Grønevik[2]基于有限元软件,对紧急脱离后隔水管的反冲响应进行了数值模拟分析。Dyngvold[3]对紧急解脱后隔水管顶部张紧系统的响应进行了分析。Pestana等[4]采用非线性阻尼弹簧模型对隔水管紧急脱离后的反冲响应进行了理论分析。Stahl等[5]对深水钻井隔水管在恶劣海况下的反冲响应进行了分析计算。李朝玮等[6-8]对深水钻井隔水管紧急解脱情况进行了介绍。张磊等[9-10]基于ANSYS有限元软件对隔水管的反冲响应进行了数值模拟分析。何新霞等[11-13]对隔水管紧急脱离后的反冲控制系统进行了研究,并提出了相关建议。目前国内针对隔水管反冲响应的研究主要集中在有限元模拟和反冲控制措施等方面,较为详细的理论求解过程未见报道。为此,笔者考虑隔水管储存的弹性势能和钻井液下泄的共同影响,建立隔水管反冲响应力学模型,在对控制方程进行求解的基础上,获得隔水管反冲响应的力学特性与主控因素。

1 力学模型

1.1 控制方程

从力学角度上讲,深水钻井隔水管紧急解脱后的反冲响应属于无限自由度弹性体在具有初始位移下的受迫振动。为简化分析,将隔水管离散成三自由度弹簧-质量-阻尼系统,所建力学模型如图1所示。

假设:①忽略隔水管的横向运动对反冲响应的影响;②忽略浮力块对轴向刚度的影响,认为隔水管轴向刚度保持一致;③将顶部张紧器对隔水管的作用视为弹簧模型;④钻井液下泄过程中产生的黏滞阻力沿隔水管轴向均匀分布。

图1 深水钻井隔水管正常作业示意图及反冲响应分析力学模型Fig.1 Schematic diagram of deepwater drilling riser in normal operation and mechanical analysis model of riser recoil response

图1中,坐标系XOt表示顶部张紧系统的升沉运动;m1、m2和m3为隔水管离散化后3个质量块的质量,其和为隔水管湿重、浮力块湿重、LMRP湿重以及顶部张紧系统的质量之和;Ff1(t)、Ff2(t)和Ff3(t)为钻井液下泄过程中作用在3个质量块上的摩阻力;K1、K2和K3为顶部张紧系统的弹簧刚度以及隔水管的轴向刚度;c1、c2和c3为作用在3个质量块上的阻尼;x1(t)、x2(t)和x3(t)为3个质量块在反冲响应过程中的位移变化,其坐标原点选择在隔水管反冲响应过程中的静态平衡位置;x*(t)为隔水管紧急解脱后LMRP与BOP之间随时间变化的距离。

根据上述假设和所建坐标系,隔水管紧急解脱后3个质量块的动态平衡方程可表示为

(1)

式中,M为质量矩阵;K为刚度矩阵;C为组逆矩阵;F(t)为合外力矩阵。

且有:

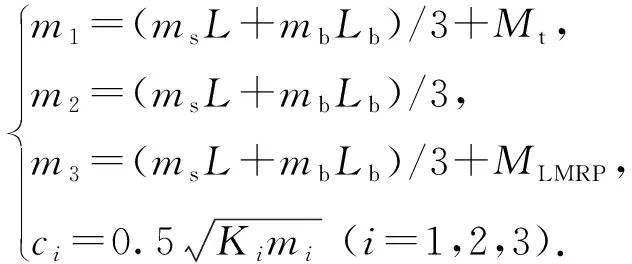
(2)

式中,ms和mb分别为单位长度隔水管和单位长度浮力块在水中的质量,kg/m;L为隔水管长度,m;Lb为浮力块的长度,m;Mt为顶部张紧系统的质量,kg;MLMRP为LMRP在水中的质量,kg。

根据假设④,钻井液下泄过程中作用在3个质量块上的摩阻力可表示为

Ffi(t)=Ff(t)/3 (i=1,2,3) .

(3)

式中,Ff(t)为钻井液下泄过程中作用在隔水管上的随时间变化的总摩阻力,N。

1.2 边界条件

LMRP与BOP脱离后,隔水管始终与顶部张紧系统连接,隔水管的反冲响应是在张紧系统升沉运动下的强迫运动。由于浮式平台的升沉运动由波浪引起,因此假设两者运动的圆频率相等。如果忽略平台升沉运动时海水的阻尼作用,则浮式钻井设备升沉运动[14]可表示为

(4)

式中,Hw为波高,m;ρw为海水密度,kg/m3;S为吃水线处浮式钻井设备与海水的接触面积,m2;md为浮式钻井设备的质量,kg;ωw为波浪圆频率,rad/s;φ为相位角,rad。

假设张紧系统的运动规律与浮式钻井设备的运动规律一致,则整个张紧器器的弹簧刚度[9,15]可表示为

(5)

式中,phi和pli分别为初始时刻活塞有杆端和无杆端气体压力,Pa;Vhi为初始时刻活塞高压腔气体体积,m3;Vli为初始时刻活塞低压腔气体体积,m3;n为气体常数,其取值通常为1.0～1.4,本文中取1.3;Ad和Ap分别为活塞有杆端和无杆端截面积,m2;N为张紧系统中张紧器的个数。

1.3 初始条件

在正常钻井过程中,隔水管在外载作用下产生轴向伸长,隔水管的反冲过程是储存在其中的弹性应变能释放的过程。因此在不计能量损耗的情况下,可根据外力的功等于隔水管的弹性应变能来计算其轴向刚度,离散化后的每段隔水管轴向刚度可表示为

(6)

其中

ω=msg-ωb.

式中,E为隔水管弹性模量,Pa;A为隔水管横截面积,m2;Ftop为隔水管顶部的拉力,N,本文中取1.35倍的隔水管湿重;ω为隔水管单位长度的重力,N/m;ωb为单位长度隔水管所受浮力,N/m。

由于3个质量块的平衡位置选择在隔水管解脱后的静态平衡位置处,因此在紧急解脱瞬间,3个质量块具有初始的位移,即

(7)

式中,ΔL为隔水管紧急解脱前的轴向总伸长量,m。

1.4 钻井液下泄黏滞阻力

深水钻井隔水管反冲过程中的外载主要来源于钻井液下泄时产生的黏滞阻力。本文中采用全液柱模型分析作用在隔水管内壁上的黏滞阻力,具体分析可参阅相关文献[2,8]。由于钻井液下泄过程比较复杂,本文中采用8阶正弦函数叠加的形式表示钻井液下泄过程中作用在隔水管内壁上的黏滞阻力,即

(8)

2 模型求解

根据振动力学基本原理,经坐标变换后,式(1)在主坐标η下可写为

(9)

其中

MP=ΦTMΦ,KP=ΦTKΦ,

CP=ΦTCΦ,P(t)=ΦTF(t).

式中,MP为主质量矩阵;KP为主刚度矩阵;Φ为振型矩阵。

对于一般条件下的有阻尼多自由度系统,经过坐标变换后MP和KP是对角阵,而CP不是对角阵,因而主坐标η下的隔水管反冲控制方程式(9)仍然存在耦合。若阻尼矩阵CP不能被对角化,且非对角元素不能被忽略,此时控制方程求解的主坐标法便不再适用,需把位移和速度看作独立的变量,采用复模态分析法进行求解。

对于一般黏性系统的矩阵特征值问题,可假设:

x=φeλt.

(10)

式中,φ为待定常数列向量;λ为待定常数。

将方程(10)带入方程(1),并令其行列式为0,得到φ有非零解的充分必要条件,即一般黏性阻尼系统的特征方程为

|λ2M+λC+K|=0.

(11)

式(11)是λ的2n(本文中n=3) 次方程,由它可以解出2n个特征值(λ1,λ2,…,λ2n)和2n个特征向量(φ1,φ2,…,φ2n),并且两两互为共轭向量。

经过进一步推导,可得一般黏性阻尼系统对任意激励的响应[16],即

(12)

其中

因本文中用8阶正弦函数表示隔水管上的黏滞阻力,因此对于每个质量块有

(13)

其中

γi=(sincj)eλit-sin(bjt+cj),

δi=(coscj)eλit-cos(bjt+cj).

将式(1)中的质量矩阵和阻尼矩阵、式(11)求得的λi和φi、式(7)及(13)带入式(12),可得到复模态分析法下的深水钻井隔水管反冲响应。

3 算例分析

3.1 算 例

以某深水钻井为例,水深2 500 m,隔水管外径为533.4 mm,内径为501.65 mm,隔水管内壁绝对粗糙度为5×10-5,海水密度为1 030 kg/m3,海水运动黏度为1.15×10-6m2/s,钻井液密度为1 680 kg/m3,钻井液运动黏度为1×10-4m2/s,波高为6 m,波浪周期为8.5 s,浮式钻井设备质量为3.3×107kg,与水面接触面积为2 500 m2,LMRP在海水中的质量为8.6 t,顶部张紧系统质量为3 t,隔水管顶部超张力系数为0.35,直接作用式张紧器参数见文献[9]。

隔水管紧急解脱后LMRP与BOP距离的变化如图2所示。由图2可以看出,隔水管紧急解脱后,在顶部张紧系统弹簧和钻井液黏滞阻力的共同作用下,反冲响应在开始的一段时间内比较剧烈;储存在隔水管内部的弹性势能被迅速释放,LMRP在0.5 s的时间内被“提拉”上升至距离水下防喷器3.05 m处;由于海水阻尼的作用,随后的轴向振动幅值逐渐减弱;当紧急解脱约5 s后,隔水管在顶部张紧系统的升沉作用下,反冲响应逐渐变得规律,最后在静态平衡位置附近做轴向振动。本算例中,隔水管紧急解脱后LMRP的振动位置始终位于BOP的上方 (x*(t)>0),因此不存在LMRP与BOP发生碰撞的可能。

图2 隔水管紧急解脱后LMRP与BOP距离的变化Fig.2 Clearance between LMRP and BOP after riser emergency disconnection

3.2 敏感性分析

3.2.1 水 深

不同作业水深时,隔水管紧急解脱后LMRP与BOP之间的距离变化如图3所示。由图3可知,隔水管的反冲响应集中在紧急解脱后的一段时间内,不同水深作业条件下,这一时间段大致相同。水深越大,隔水管紧急解脱后LMRP与BOP之间的最大距离越大。这是因为水深越大,隔水管正常钻井作业时产生的拉伸量越大,储存的弹性势能越大;并且由于隔水管的长度不同,其振动达到平衡时的LMRP位移也不同,4种水深条件下,LMRP最后的振动平衡位置距BOP分别为0.80、1.45、2.20和2.98 m。隔水管紧急解脱后LMRP的振动位置始终位于BOP的上方。但LMRP被拉升的高度越大,对张紧系统的活塞和月池的威胁越大。因此在同样的作业条件下,水深越大,隔水管紧急解脱的安全作业窗口越小。

图3 水深对隔水管紧急解脱后LMRP与BOP间距的影响Fig.3 Influence of water depth on clearance between LMRP and BOP after riser emergency disconnection

3.2.2 波 高

不同波高时,隔水管紧急解脱后LMRP与BOP之间的距离变化如图4所示。

图4 波高对隔水管紧急解脱后LMRP与BOP间距的影响Fig.4 Influence of wave height on clearance between LMRP and BOP after riser emergency disconnection

由图4可知,波高越大,隔水管的反冲响应越剧烈,LMRP被“提拉”的高度越大,最大距离出现的时刻均为隔水管紧急解脱后约0.5 s;并且随着波高的增大,在隔水管底部脱离后,LMRP的振动位移会出现负值,这意味着LMRP运动到了BOP的下方,因此存在LMRP与BOP发生碰撞的可能,会对水下井口的安全性产生威胁。本算例中,当波高为10 m时,LMRP在解脱后的1.0 s,振动到BOP以下0.33 m;当波高为12 m时,LMRP在解脱后的1.2 s,振动到BOP以下1.04 m,在解脱后的2.5 s,振动到BOP 以下0.29 m。因此对于相同配置的隔水管系统,随着波高的增大,需采取控制措施确保LMRP不与BOP发生碰撞。

3.2.3 顶部张紧器弹簧刚度

在本文前述的计算中,均采用顶部张紧系统的最大弹簧刚度来分析,在隔水管紧急解脱后,由于某些不可预知的因素可能会导致张紧系统发生失效或损坏,使其弹簧刚度降低,当张紧器的弹簧刚度出现不同程度的降低时,LMRP与BOP之间的距离变化如图5所示。

图5 顶部张紧器弹簧刚度对隔水管紧急解脱后LMRP与BOP间距的影响Fig.5 Influence of spring stiffness of top tensioner on clearance between LMRP and BOP after riser emergency disconnection

由图5可知,张紧器刚度越小,隔水管的反冲响应越剧烈,LMRP向上或向下振动的最大值均增大,对隔水管实施安全的紧急解脱不利。本算例中,当张紧器刚度降低到最大值的50%时,发生紧急脱离后LMRP首先向下振动,随后LMRP出现在BOP下方0.98 m。因此如果张紧器弹簧刚度过低,当隔水管发生紧急脱离后,张紧器没有足够的能力将隔水管“提拉”上来,在钻井液下泄黏滞阻力的作用下,LMRP会先向下振动到最大负值位移后再向上运动,并且在随后的振动过程中仍有可能与BOP发生碰撞。因此,为保证隔水管实施安全的紧急解脱,需确保顶部张紧器弹簧刚度不被降低。

3.2.4 解脱相位角

将浮式钻井设备的正弦形式的升沉运动作为隔水管顶部的力学边界条件,然而LMRP脱离的时刻并不一定是浮式钻井设备升沉运动的开始时刻,因此二者之间存在一定的相位差。当LMRP在不同时刻解脱,φ的取值分别为0°、45°、90°、135°、180°、225°、270°和315° 时,LMRP与BOP之间的最大位移分别为3.05、3.11、3.18、3.30、3.38、3.29、3.17和3.12 m。可以看出,解脱初相角对隔水管的反冲响应影响不大。本算例中,不同的解脱初相角情况下,LMRP始终在BOP上方振动,且振动的最大位移变化不大。

4 结 论

(1)采用复模态分析方法可以考虑隔水管在正常钻井作业过程中储存的弹性势能和钻井液下泄时产生的黏滞阻力的共同影响,还可以考虑隔水管反冲响应控制方程中阻尼矩阵非对角项元素的影响。

(2)在同样的作业条件下,水深越大,隔水管紧急解脱的安全作业窗口越小;波高越大,隔水管的反冲响应越剧烈;张紧器刚度越小,LMRP与BOP发生碰撞的可能性越大;解脱相位角对隔水管的紧急解脱作业影响不大。