基于格子玻尔兹曼方法的致密砂岩驱替模拟
唐明明, 卢双舫, 辛 盈, 檀洪坤, 刘雪萍, 时 贤, 张洪亮
(1.中国石油大学(华东)深层油气重点实验室,山东青岛 266580; 2.中国石油国际勘探开发有限公司,北京100621;3.中国石油大学(华东)石油工程学院,山东青岛266580; 4.中国石油大庆油田第九采油厂地质大队,黑龙江大庆 163853)
随着能源需求的日益攀升以及常规油气资源的日渐枯竭,具有较大资源潜力的非常规油气,特别是致密油气,已经开始重塑全球能源格局[1-3]。然而目前致密油藏衰竭式开发的平均采收率仍然较低(4%~10%)[4]。水驱作为油藏能量补充的重要手段,其在致密油藏中的应用研究受到人们的广泛关注[5-6]。目前,致密砂岩岩心驱替物理试验研究,可以分析水驱采收率及残余油分布特征,但是岩心物理试验成本高、周期长、计量困难,并且难以分析流体三维动态变化规律。通过油藏尺度水驱模拟研究可以得到致密油藏水驱产能特征,然而主要针对宏观尺度分析,无法揭示微观渗流机制[7-13]。笔者基于三维数字岩心建模方法和格子玻尔兹曼多相流方法[14-15],构建致密砂岩三维数字岩心模型,通过恒压条件与恒速条件下的模拟,分析致密砂岩水驱的三维微观过程,研究不同条件下的驱替效率和换油率。
1 模拟方法
格子玻尔兹曼方法(LBM)的核心是建立微观尺度与宏观尺度的桥梁,它不考虑单个粒子的运动而是将所有粒子的运动视为一个整体,粒子的整体运动特性由分布函数表示,粒子存在的空间用格子排列表示[16]。目前,对于三维格子排列模型主要有3种D3Q15、D3Q19和D3Q27,其中“3”代表格子排列模型的维度,“15”、“19”和“27”代表速度模型中的离散的速度分量。速度分量越多,数值模拟的准确性越高。考虑到模型孔喉结构复杂,本次模拟采用D3Q27模型(图1),以达到最高计算精度。
D3Q27的LMB的模型如图1所示,其中数字标注的为离散速度矢量(共27个离散速度矢量)。第0个离散速度矢量位于格子单元中心,离散速度为0,其他的离散速度矢量分为以下几种:①从模型中心指向面的中心点的离散速度矢量(图1中1~6),其离散速度为1;②从模型中心指向各边的中点的离散速度矢量(图1中7~18),其离散速度为2;③从模型中心指向模型顶点的离散速度矢量(图1中19~26),其离散速度为3。按照LBM理论,所有离散速度值均为无量纲形式。
在D3Q27模型中,分布函数满足以下格子玻尔兹曼输运方程[14-20]:
fα,k(x+ekΔt,t+Δt)-fα,k(x,t)=
(1)
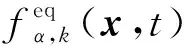
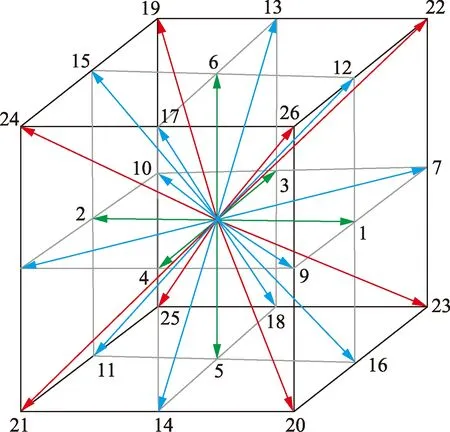
图1 格子玻尔兹曼D3Q27模型Fig.1 D3Q27 model of lattice Boltzmann method
方程式(1)可由BGK方程导出,BGK方程[14-20]为
(2)
其中弛豫时间λα与流体黏度μα存在以下相关关系:
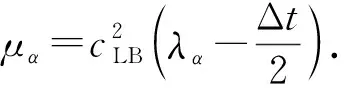
(3)
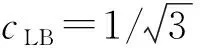


(4)
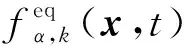
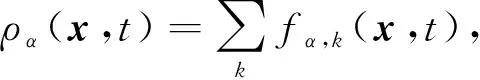
(5)
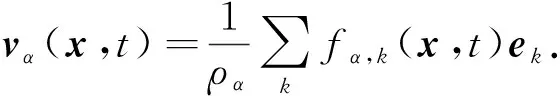
(6)
在D3Q27模型的基础上,采用Shan-Chen模型开展多相流模拟研究。Shan-Chen模型的基本思想是利用一个依赖于局部密度和相互作用强度的势函数来表示不同相态分子间的相互作用[23-24],已有的Shan-Chen模型研究表明,在D3Q27模型中加入合适的势函数,不同相流体会自动分离[25-26]。Shan-Chen模型已成功地应用于多相流的广泛研究中,特别是多孔介质中的多相流[25-26]。
Shan-Chen模型中,作用于流体相α的总力Fα,ff(x,t)[27]可以表示为
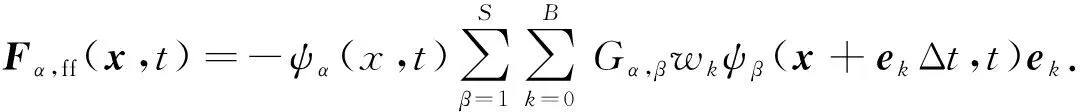
(7)
式中,ψα(x,t)为伪势;α和β表示α相流体和β相流体;Gα,β为相α相与β相之间的相互作用强度;S为流体相的数目;B为离散速度矢量的数目。
基于相互作用力,对于多相流LBM提供了模拟方法。多相流的LBM模拟通过协同速度v(x,t)′实现,其中
采用格子量纲,而被Fα,ff(x,t)改变的瞬时速度vα(x,t)[24]可以表示为
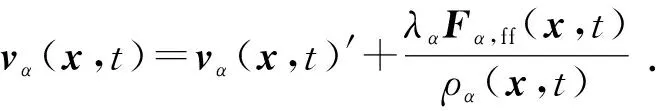
(8)
由于本文中只考虑两相流,因此Gα,β在之后模拟中始终为常数G,通过改变相互作用强度矩阵中的Gα,β来改变流体相的状态[25-26]。
接触角也由固相和流体相之间的相互作用力控制,可将式(7)中的ψβ(x+ekΔt,t)改为π(x+ekΔt,t),由此流体相和固体表面的作用力[18-19]可以表示为
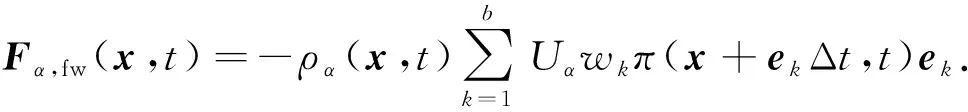
(9)
式中,Uα为流体相与固体相之间的相互作用强度,采用格子量纲;π(x+ekΔt,t)等价于1代表固体,等价于0代表流体相。因此作用在流体节点上的总作用力为Fα(x,t)=Fα,ff(x,t)+Fα,fw(x,t)。
2 试验数据
本次研究样品Y采自松辽盆地龙26致密油区块W井高台子油层。Y样品直径DY为2.5 cm, 轴长LY为10 cm,孔隙度φe为9.7%,渗透率Ke为0.95×10-3μm2。Y样品采回后,在实验室内分为2段,其中一段为用于进行CT扫描试验的样品A,另外一段为用于进行室内驱替试验的样品B,其中样品B长度为9 cm。再将B样品分割为B1和B2两个样品,其长度均为4.2 cm。B1样品应用于恒压驱试验,B2样品应用于恒速驱替试验。其中物理试验选用二氯甲烷和丙酮体积比为3∶1的混合有机溶剂作为洗油溶剂。模拟地层水为NaHCO3型,矿化度为5 497 mg/L。驱替使用的模拟油为淡黄色煤油,密度为0.8 g/cm3,黏度为1.0~2.0 mm2/s。每次试验前首先利用洗油溶剂对致密砂岩样品进行洗油,时间为72 h,之后进行24 h的高温烘干,烘干温度为110 ℃。烘干完成后,将样品放入饱和仪内抽真空,饱和模拟地层水,饱和8 h。为了保证数值模拟试验与物理试验的可对比性,恒压驱替条件下,物理试验和数值试验按照等压力梯度原则设计试验压差,恒速驱替条件下,按照流速相同原则,设定样品端口流量。
内部控制评价主体由内部评价主体和外部评价主体两部分组成,两个评价主体分别有不同的评价目标,因此就使得两个主体之间必然会产生矛盾。两个评价主体会在考虑自身利益的基础上进行内部控制评价,这就使得在内部控制评价过程中两个评价主体的效率有一定的差异。公司内部评价主体在内部控制评价时更注重公司的经营战略目标,这从很大程度上保证了公司战略目标的顺利实现;而外部评价主体关注的是报告的合法合规性,外部评价主体在保证自身独立、权威的同时协助政府监督机构对所评价公司的内部控制进行监督审查,提高所评价公司的内部控制质量,从而促进会计稳健性的提高。根据分析提出第一个假设:

图2 三维数字岩心构建Fig.2 Three dimensional digital rock construction
数值模拟中使用的三维数字岩心采用A样品,使用ZEISS CT 3D X射线显微镜进行样品扫描,其扫描分辨率为1.0 μm,扫描视场为1 747 μm,扫描电压为50 kV,电流为50 mA,曝光时间0.7 s,扫描总时长2 h。图2(a)为样品的一张CT扫描图像局部(400 μm×400 μm),图片分辨率为1 μm/像素。为了提高计算精度,对CT图像数据进行了10倍加密,加密后像素大小为0.1加密。应用中值滤波处理,中值滤波处理使骨架与孔隙之间的过渡变得更加平滑自然,并且去除了矿物表面的孤立噪点。中值滤波利用MATLAB中medfilter2滤波函数,采用最邻近中值滤波模板参数。滤波之后通过设定分割阈值,对图像组分进行分割,将灰度图转化为二值的黑白图像,如图2(b),其中黑色代表孔隙,白色代表骨架。经过二值化分割后的图像沿着切片纵向叠加并通过阈值分割提取孔隙,得到致密砂岩样品的三维数字岩心。然后基于二值化模型,计算数字岩心的孔隙度和渗透率。然后将数字岩心得到的物性数据与试验数据进行对比,不断优化分割阈值,最终优化分割阈值为Th=51,数字岩心孔隙度和渗透率分别为9.9%和1.02×10-3μm2。基于上述数字岩心模型,利用格子玻尔兹模型,开展驱替模拟。格子玻尔兹曼模型中,固体边界采用全反弹模型。模拟物理空间步长为Δxp=1×10-7m,物理时间步长为Δtp=1×10-9s,格子特征速度为uLB=1×10-5,物理特征速度为up=1×10-3m/s。
为了缩减模拟时间,从重构的三维数字岩心中截取尺寸为210 μm×80 μm×40 μm的模型A(图2(c))作为LBM水驱模拟平台,模拟像素精度为0.1 μm,模拟结果输出间隔为0.1 s。模型参数设置如下:模拟温度T=100 ℃,压力条件p=19 MPa,模拟地层水黏度μw=1.0 mPa·s,模拟地层原油黏度μo=1.45 mPa·s,模拟水相密度ρw=1.0 g·cm-3,模拟原油密度ρo=0.78 g·cm-3。
3 模拟结果
结合研究区实际参数设定模型系统参数后,可应用给予Shan-Chen模型的D3Q27模型开展水驱模拟过程模拟。模拟一共分为2个阶段:阶段Ⅰ为充注油阶段,阶段Ⅱ为水驱油阶段。阶段Ⅰ充注油的目的是为阶段II水驱油模拟生成初始油水分布。模型计算中时间步长度10-7s,为了加快输出和后处理的速度,每间隔0.1 s设定一个输出步(记s为输出步数量)。
阶段Ⅰ充注油阶段,该阶段油相充注速度为100 μm/s,从模型左侧注入油相,恒速驱替到含水饱和趋向不变为止。图3为油充注过程模拟得到的油水分布图(其中固体矿物透明化处理)。图3(a)为初始饱和水状态,模拟样品烘干后饱和水的状态;图3(b)~(d)为充注过程中含油饱和度分布。图3表明:①随着充注的进行油相充填的孔隙不断增多;②油相前缘为凸状形态(图3(b));③模型右侧靠近出口端的水相分布大于模型入口端附近的水相分布;④充注过程中出现了黏性指进现象(图3(c));⑤在被油填充的孔隙壁面上仍然发现有润湿相的水存在(图3(d)),有一部分吼部较小的孔隙在油充注过程中未被填充,油相优先填充了后续孔吼半径较大的孔隙。
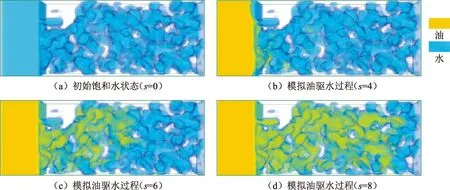
图3 油驱水过程模拟及岩心中油相初始分布Fig.3 Simulations of oil displacing water and initial oil distribution in digital rock
阶段II水驱油阶段,该阶段在阶段Ⅰ之后进行,从模型左侧注入水相。阶段Ⅱ水驱油又根据注入条件又分成恒压条件下水驱油和恒速条件下水驱油两类。其中恒压条件下水驱油为研究不同注入压力对驱替效率的影响,本次研究共设定了4个注入压差,4个模拟方案分别为pH2O_p1、pH2O_p2、pH2O_p3和pH2O_p4(表1)。另外恒速条件下水驱油为研究不同注入速度对驱替效率的影响,本次研究共设定了4个注入速度,4个模拟方案分别为vH2O_v1、vH2O_v2、vH2O_v3和vH2O_v4(表1)。

表1 水驱数值模拟方案
3.1 恒压条件下三维动态驱油过程模拟
恒压条件下水驱油过程中油水分布变化与恒速驱替过程中相似,对比图4(a)和(b)可以看出高压p2条件下模型pH2O_p2的驱替速度明显高于p1条件下pH2O_p1模型的驱替速度。同时恒压驱替过程中,最终残余油分布区域也与恒速驱替下的残余油分布区域相似。

图4 恒压条件下水驱油过程模拟Fig.4 Numerical simulation of water displacing oil with constant injecting pressure
3.2 恒压驱替效率和换油率
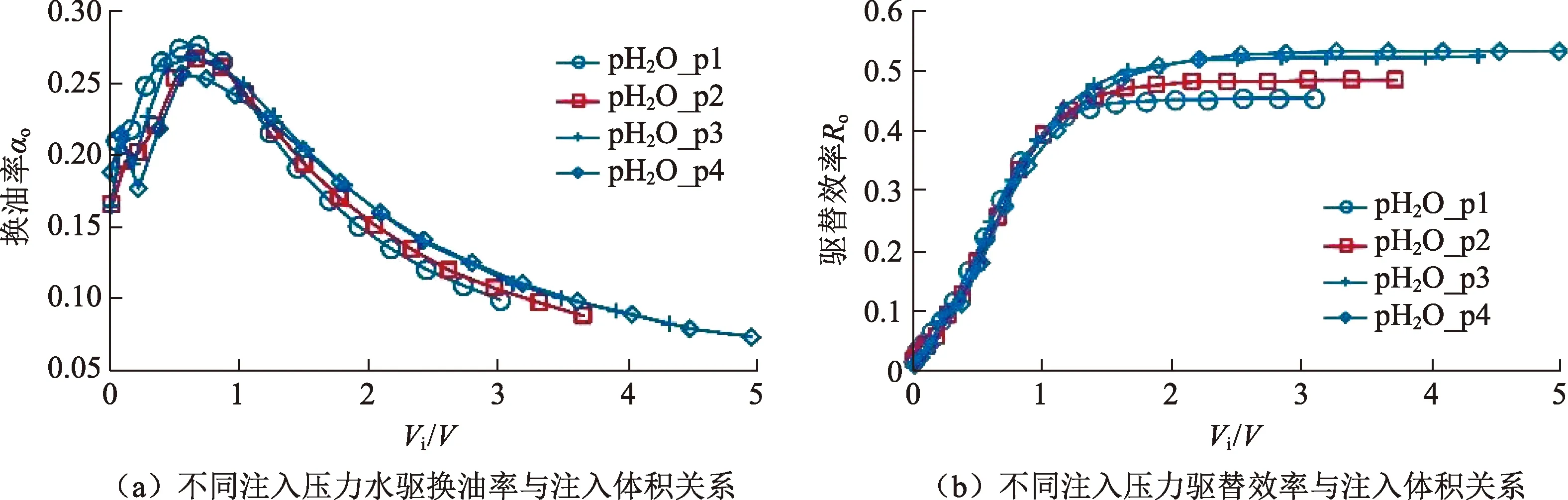
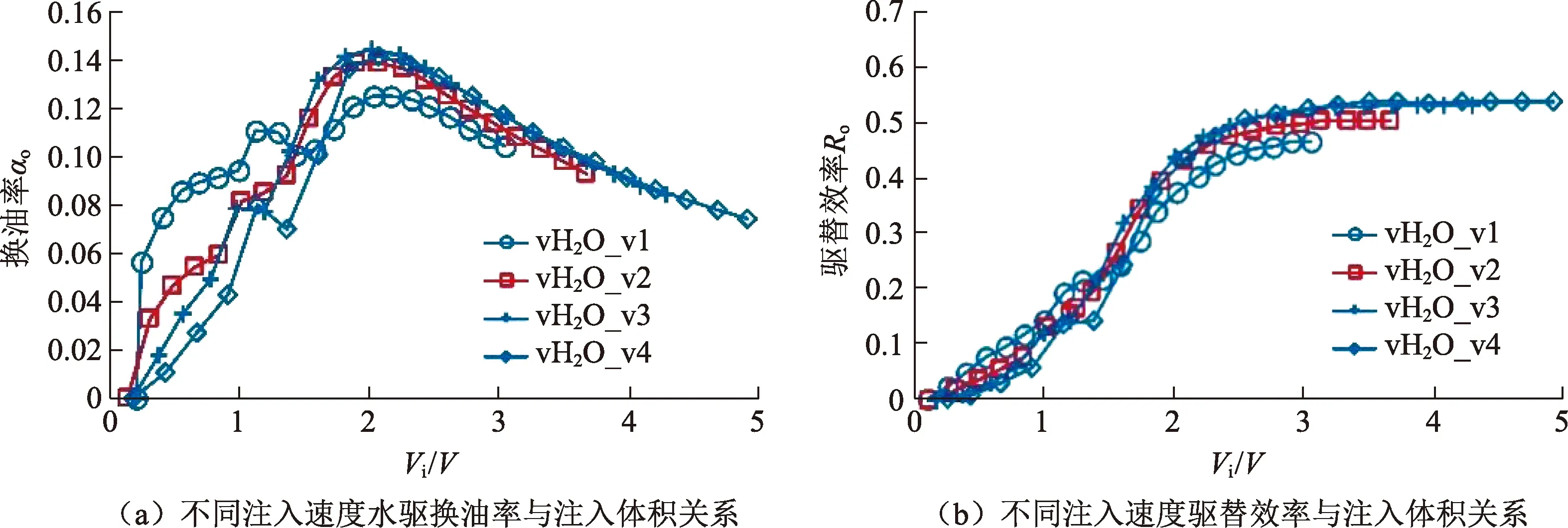
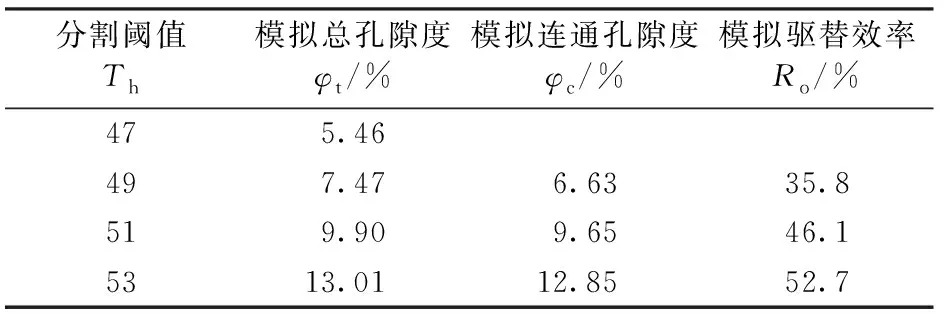
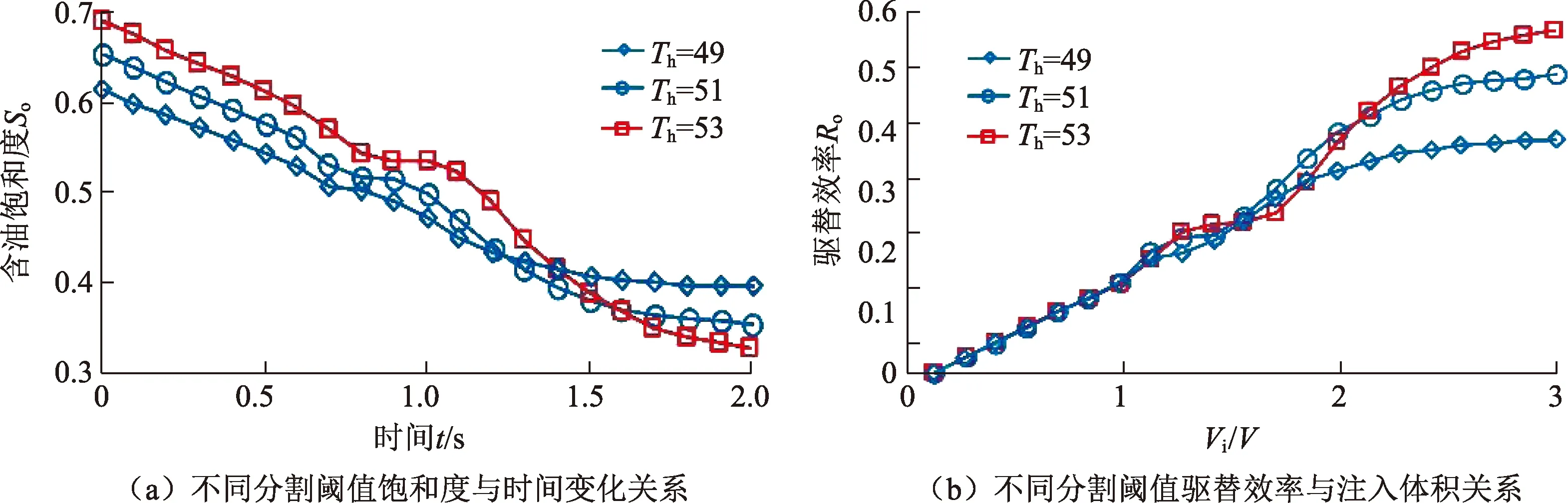
基于LBM水驱模拟结果,可以计算恒压条件下含油饱和度随着注入水量的变化,以及驱替效率和换油率随着注入量的变化。图5为不同注入压力水驱饱和度随时间变化关系。从图5可以看出:①恒压注入条件下含油饱和度随着水驱的进行开始逐渐下降;②4个模型的含油饱和度下降速度关系为pH2O_p1 图5 不同注入压力水驱饱和度随时间变化关系Fig.5 Curves of oil saturation versus time with different injecting pressure 图6为不同注入压力水驱换油率和驱替效率与注入体积关系(图中横坐标为注入液量Vi与数字岩心模型孔隙总体积V的比值)。从图6可以看出:恒压条件下水驱换油率同样随着注入量的增加先增加后减少;4种注入压力下,最优换油率注入体积为1.1V;恒压水驱驱替效率随着注入量增加首先增加,然后渐进平稳;当注入量大于1.5V以后,驱替效率逐渐趋向于稳定;当累积注入量为2.4V时,不同注入压力下的驱替效率基本不变。对比不同驱替压差模拟条件下的含油饱和度-时间变化曲线以及驱替效率-注入体积曲线可以发现,致密油恒压驱替压差-驱替效率曲线存在最优拐点。当驱替压差从3.0×104Pa增加到3.5×104Pa后,模拟驱替效率仅增加了4.4%,而当驱替压差从3.5×104Pa增加到4.0×104Pa时,模拟驱替效率仅增加了0.6%。 图6 不同注入压力水驱换油率和驱替效率与累积注入体积关系Fig.6 Curves of oil exchange ratio versus cumulative injection volume and displacement efficiency versus cumulative injection volume with different injection pressure 表2为最终驱替效率-注入压力统计。驱替试验所用压力梯度与模拟所用压力梯度相同。对比试验驱替结果和数值模拟驱替结果表明,数值模拟得到的恒压水驱的平均驱替效率为47.3%,物理驱替试验得到恒压水驱平均驱替效率为44.7%,4种条件下数值模拟驱替结果与室内试验结果吻合度均大于90%。 表2 不同注入压力下最终驱替效率Table 2 Ultimate displacement efficiency with different injection pressure 恒速条件下共开展了4种不同注入速度下的水驱油模拟(图7)。vH2O_v1、vH2O_v2、vH2O_v3和vH2O_v4的水驱油模型,均基于相同的模型,以增加模拟的可对比性,同时4个模型中也使用了相同的油充注结果,消除初始模型的影响。由图7可以看出:①随着水驱油过程的进行,油相分布逐渐减少,水相分布逐渐增加;②水相分布也出现黏性指进现象,在水相扫略过程中部分油相滞留下来;③vH2O_v2模型水相驱替速度大于vH2O_v1(图7(a)和(b));④vH2O_v1和vH2O_v2模型,最终残余油相分布区域相似(图7(a)和(b)),都集中在模型的中部区域。图7(c)和(d)为vH2O_v3和vH2O_v4模型的驱替过程模拟结果,与图7(a)和(b)对比表明,最终残余油分布与vH2O_v1和vH2O_v2模型相似,可见对于相同的孔隙空间分布,采用水驱油方式时,最终残余油分布的有利区域随注入速度改变较小。 根据LBM水驱模拟结果,通过综合计算可以给出含油饱和度随着注入水量的变化,并据此计算了驱替效率和换油率随着注入量的变化。图8为不同注入速度水驱饱和度-时间变化关系。从图8可以看出:①含油饱和度随着水驱的进行开始逐渐下降;② 4个模型的含油饱和度下降速度关系为vH2O_v1 图9为不同注入速度水驱换油率和驱替效率与注入体积关系。从图9可以看出:水驱换油率随着注入量的增加先增加后减少;4种注入速度下,最优换油率注入体积为2.2V;水驱驱替效率随着注入量增加首先增加,然后渐进平稳;当注入量大于2V以后,驱替效率逐渐趋向于稳定;当累积注入量为3V时,不同注入速度下的驱替效率关系为vH2O_v1 图7 恒速条件下水驱油过程模拟Fig.7 Numerical simulation of water displacing oil with constant injecting velocity 图8 不同注入速度水驱饱和度随时间变化关系Fig.8 Curves of oil saturation versus time with different injecting velocity 图9 不同注入速度水驱换油率和驱替效率与累积注入体积关系Fig.9 Curves of oil exchange ratio versus cumulative injection volume and displacement efficiency versus cumulative injection volume with different injection velocity 表3为不同注入速度水驱最终驱替效率-注入速度统计结果。试验所用注入速度与模拟注入速度相同。表3表明随着注入速度的增加,最终驱替效率逐渐增加。这与图8和9的分析结果一致,总体来看,数值模拟得到的恒速水驱的平均驱替效率为49.6%,驱替物理试验得到的恒速水驱的平均驱替效率为47.1%,4种注入速度条件下,试验驱替效率与模拟驱替效率的吻合度均大于90%。 表3 不同注入速度下最终驱替效率Table 3 Ultimate displacement efficiency with different injection velocity 分割阈值是影响数字岩心物性的关键参数之一,在将灰度图转化为二值的黑白图像过程,分割阈值控制着孔隙的连通性,也随之影响模拟结果。为了进一步分析分割阈值对于模拟结果的影响。选取4个分割阈值,分别为47、49、51和53,构建相应的数字岩心,并以恒速驱替为例,分析分割阈值对于驱替效果的影响。表4为分割阈值对数字岩心模型总孔隙度和连通孔隙度的影响。结果表明,数字岩心总孔隙度随着分割阈值增大而升高,连通孔隙度也相应升高。同时表4表明,随着分割阈值的减少,不连通孔隙在总孔隙度中所占的比例也不断提高,当分割阈值小于等于47时,孔隙无法建立连通网络。 表4 数字岩心模型分割阈值对总孔隙度和连通孔隙度的影响Table 4 Effects of threshold of digital rock model on the total porosity and connective porosity 图10为不同分割阈值、相同注入速度(25 μm/s)条件下,驱替数值模拟得到的饱和度-驱替时间变化曲线(图10(a))和驱替效率-注入体积变化曲线(图10(b))。结果表明分割阈值对于初始含油饱和度和驱替效率存在较强的控制作用。分割阈值与初始含油饱和度和驱替效率存在正相关关系,分割阈值越小,有效的连通孔隙度越小,通过阶段I充注试验得到的初始含油饱和度越小,最终驱替效率也较小。对比不同分割阈值得到的模拟驱替效率与试验得到的驱替效率(表4),表明当分割阈值Th=51时得到的连通孔隙度为9.65%,与试验气测孔隙度(9.7%)符合较好,同时模拟得到的驱替效率(46.1%)也与试验得到的驱替效率(45.9%)符合较好;而当分割阈值变为49时,数字岩心的连通孔隙度(6.63%)与试验气测孔隙度(9.7%)符合度变差,模拟得到的驱替效率与试验驱替效率符合度也相应变差。 图10 数字岩心模型分割阈值对水驱饱和度和驱替效率影响关系Fig.10 Effects of threshold of digital rock model on oil saturation and displacement efficiency (1)通过联合三维数字岩心模型和Shan-Chen格子玻尔兹曼多相流模拟方法,可以定量分析致密油充注及水驱微观过程,以及含油饱和度、驱替效率和换油率动态变化特征。 (2)恒速状态下水驱换油率随着注入量的增加先增加后减少。4种注入速度下,最优换油率注入体积为2.2V;恒速状态下水驱驱替效率随着注入量增加首先增加,然后渐进平稳。当注入量大于2V以后,驱替效率逐渐趋向于稳定;当累积注入量为3V时,不同注入速度下的驱替效率关系为vH2O_v1 (3)恒压注入条件下含油饱和度随着水驱的进行开始逐渐下降。4个模型的含油饱和度下降速度关系为pH2O_P1 (4)恒压条件下水驱换油率同样随着注入量的增加先增加后减少;4种注入压力下,最优换油率注入体积为1.1V;恒压水驱驱替效率随着注入量增加首先增加,然后渐进平稳;当注入量大于1.5V后,驱替效率逐渐趋向于稳定;当累积注入量为2.4V时,不同注入压力下的驱替效率基本不变。 (5)数字岩心分割阈值对于模拟初始含油饱和度和驱替效率存在较强的控制作用,分割阈值越小,有效的连通孔隙度越小,充注模拟得到的初始含油饱和度越小,最终驱替效率也较小。
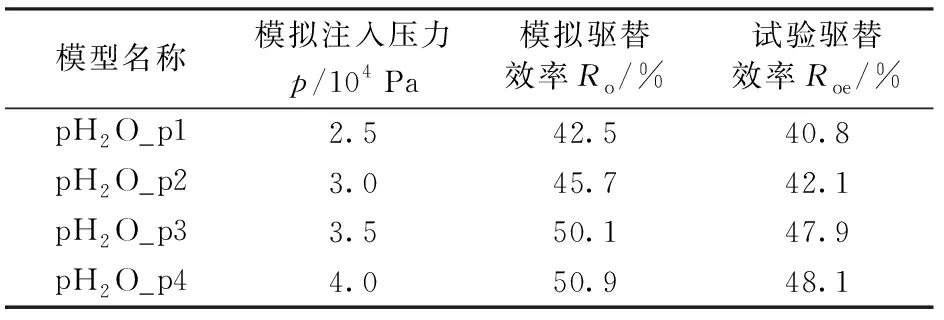
3.3 恒速条件下三维动态驱油过程模拟
3.4 恒速条件下驱替效率和换油率


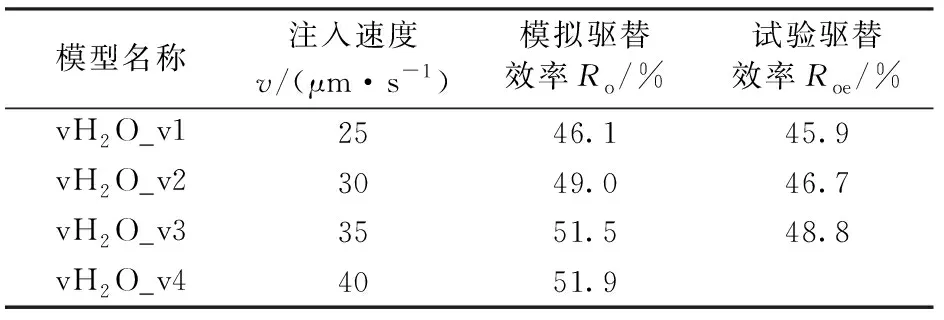
3.5 分割阈值对模拟结果的影响讨论
4 结 论

