时滞分布参数系统间歇非周期中和控制器设计
周笔锋,罗毅平
1.湖南电气职业技术学院 风能工程学院,湖南 湘潭411101
2.湖南工程学院 电气信息学院,湖南 湘潭411104
3.湖南科技大学 机电工程学院,湖南 湘潭411201
4.湖南工程学院 风电装备与电能变换协同创新中心,湖南 湘潭411104
1 引言
实际生活中许多物理系统都具有时空特性,其行为必须依赖于时间和空间位置,例如热扩散、流体换热器、化学工程、旋转梁、可变几何形状静电微致动器、集成和消防神经元等等,文献[1-7]中有详细的介绍。而这些系统的时空过程被称为分布参数系统(DPSs)。近年来,由于实际应用的需要,例如流体在多孔介质中的流动、湿纺碳纤维成形过程、火箭推进器动力学、化学反应、描述生物种群的关系等,分布数系统的控制问题受到了广泛的关注。大量的实际过程[8-13],例如流化床和填充床反应器、涂覆工艺、薄膜的化学气相沉积和生物过程等,通常通过拟线性抛物型偏微分方程PDE 系统来建模。所以根据能量守恒定律,构建拟线性抛物型偏微分方程,以拟线性抛物型偏微分方程建模研究分布参数系统控制问题已经是国内外相关领域学者的重点研究课题[14-21]。
文献[14]中,Luo等针对拟线性抛物型偏微分方程,设计控制器,利用Lyapunov 稳定性定理结合LMI 计算方法,得出了分布参数系统指数稳定控制器存在的充分条件。文献[15]中,Demetriou针对具有边界观测与控制的PDEs 网络系统同步问题,提出了一种自适应控制方案,研究系统同步稳定性问题。文献[16]中,Babaei等针对工艺参数未知的化学分布参数系统,构建半线性偏微分方程,利用Lyapunov稳定性定理,研究了其自适应输出反馈控制问题。文献[17]中,Wu 等运用半线性抛物线偏微分方程(PDEs),论述了一类非线性分布参数系统的模糊边界控制设计问题,通过采用Lyapunov 直接法和向量值Wirtinger不等式建立足够的指数稳定条件,并提出了控制方法的优点和有效性。文献[18]中,Yuan等针对一类具有耦合性质的时滞分布参数系统,构建拟线性抛物型偏微分方程并结合Lyapunov 稳定性定理,研究了系统节点的同步问题。
文献[21]中,周等首次提出了中和控制方案,并以其先进的控制思想及优越的工程适应性被许多技术工作人员应用,但针对分布参数系统,中和控制的行为过程在时间及空间位置上是一个自发的控制过程,在每个空间位置节点上,其控制不一定是持续连续的,控制周期可能是以一种不连续的间歇控制方式实现的,而对于所有节点,其间歇控制特性又不尽相同,所以本文在此基础上,对中和控制方案进行改进,将中和控制方法与非周期间歇控制方案结合,研究系统稳定性就显得尤为重要。
在实际系统中,时滞现象是普遍存在的[14,18,21-23],在系统的信息传递、信号检测过程中通常具有滞后现象。本文从时滞分布参数系统出发,设计间歇非周期中和控制器,研究时滞分布参数系统的间歇非周期中和控制就显得尤为有意义了。
基于此,本文针对一类时滞分布参数系统,设计非周期间歇中和控制器,研究系统镇定性。利用Lyapunov稳定性理论并结合LMI处理方法,得出时滞分布式参数系统间歇非周期中和控制器存在的充分条件。最后结合所给条件,给出一个数值仿真说明其有效性。
2 问题描述
考虑下列具有时滞特性的分布参数系统:
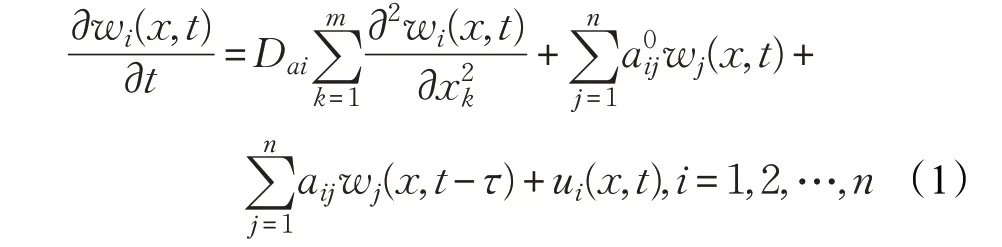
将系统变为矩阵形式,即为:
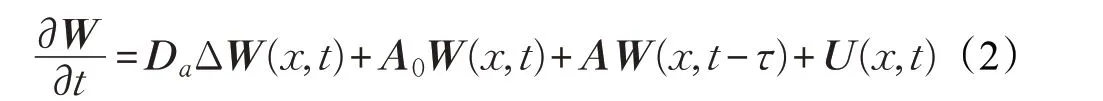
其中,(x,t)∈Ω×R+,Da=(Dai)n×n>0,τ 为时滞,和为常数矩阵为具有光滑边界∂Ω 的有界区域,且mes Ω >0,U(x,t)=(u1(x,t),u2(x,t),…,un(x,t))T∈Rn为控制输入,状态变量W(x,t)=(w1(x,t),w2(x,t),…,wn(x,t))T∈Rn,为Ω 的Laplace扩散算子,其初始边界条件为:
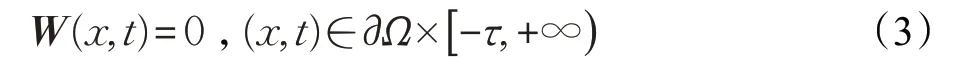
或
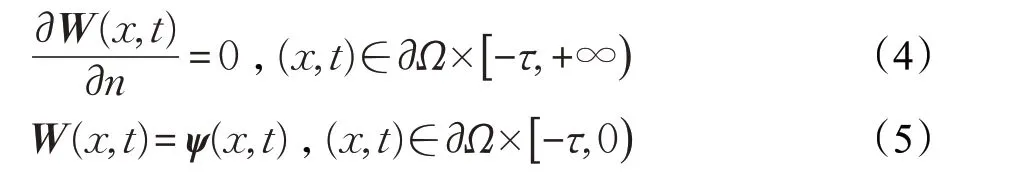
其中,n 为∂Ω 的单位外法向量,ψ(x,t)为适当光滑的函数。
为使系统(1)达到稳定,设计如下分布动态反馈控制器:
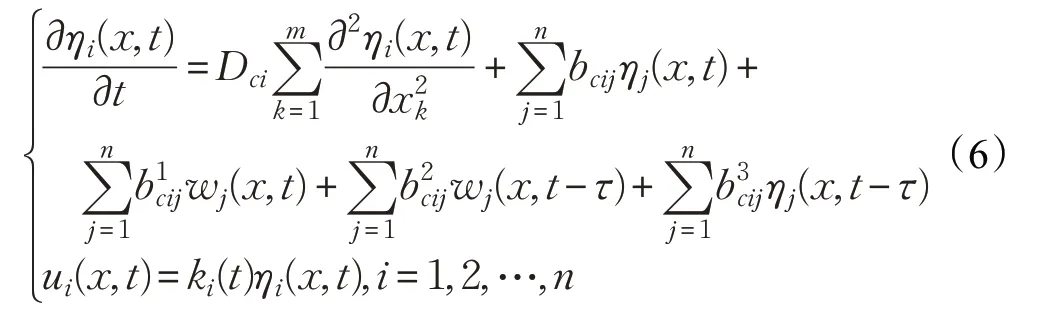
其中,ki(t)为间歇控制器的控制增益,满足:

其中,j=1,2,…,[ )tij,tij+1表示节点i 的一个周期,[ )tij,sij表示节点i 的周期内的控制时间,[ )sij,tij+1表示节点i的周期内非控制时间。将控制系统(6)变为矩阵形式,即为:
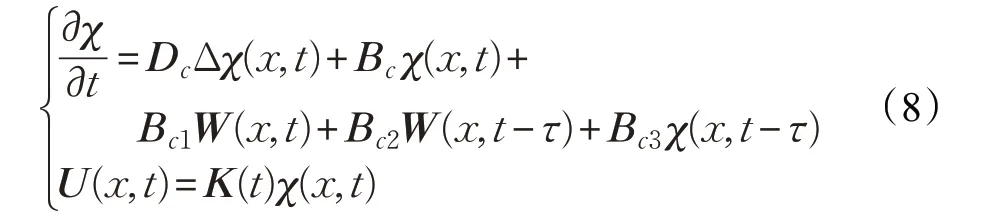
其中,χ(x,t)=(η1(x,t),η2(x,t),…,ηn(x,t))T∈Rn为状态变量
为控制器参数,控制律U(x,t)为系统(2)输入控制,K(t)=diag(k1(t),k2(t),…,kn(t)),控制系统(8)初始边界条件为:
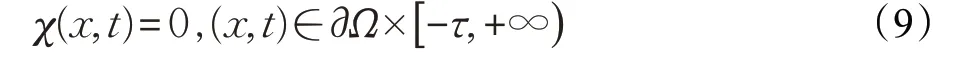
或

假设1 考虑所有节点,考虑一般实际情况,对于如式(7)所示间歇控制器,其某节点的控制时间[ tij,sij)长度一般远大于对应周期的非控制时间[ sij,tij+1),基于此,本文做出如下假设,在整个中和控制方案时间内,对于所有节点,其间歇反馈控制增益满足:
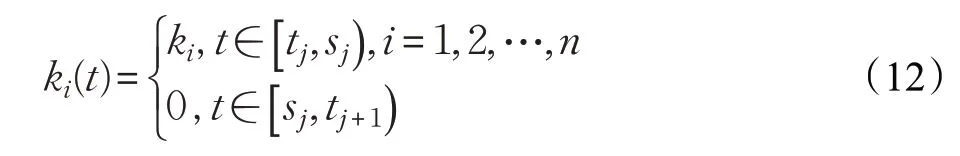
如图1 所示,[tj,tj+1)为控制周期,[ tj,sj)控制周期内的控制时间,[ )sj,tj+1表示节点i 的控制周期内非控制时间。
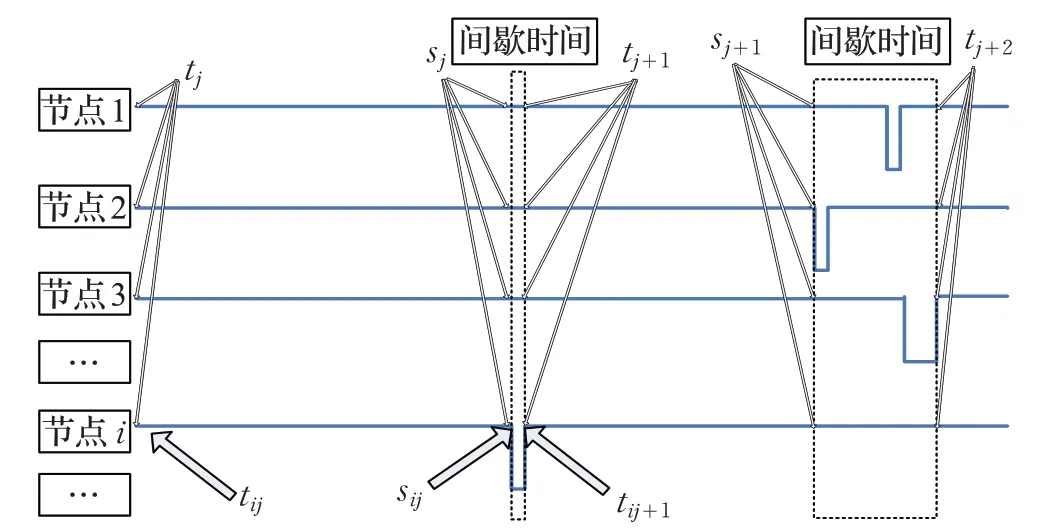
图1 间歇控制原理图
注1 对于假设1,式(12)为假设情况,当t ∈[ )sj,tj+1时,ki(t)=0 不代表真正意义上系统在此时间段没有节点被控制,而是代表由于系统此时间段内受控节点数目较少或此时间段较短且不是所有节点全部实现被控制状态,所以此时间段内,其对系统的其他控制节点的控制作用不进行考虑。
假设2[24]对于非周期间歇控制器,存在两个正标量0 <θ <ω <+∞,对于所有j=0,1,2,…,满足:

对于式(13),对于非周期间歇控制器,尽管控制时间跨度在每个周期内不一样,但是对于所有周期,其每个控制周期内控制时间宽度都不小于θ,其每个周期内控制时间间歇宽度都不大于ω-θ,定义:

ψ 表示所有控制周期内最大间歇宽度比,可得0 ≤ψ <1,若ψ=0,表示系统处于连续控制状态,一般情况假设ψ ∈(0,1)。
引理1[24]对于所有j=0,1,2,…,定义:

引理2[25]存在任意的m 维实变向量X,Y,K 为正定对称矩阵,P ∈Rm×m,则下列矩阵不等式成立:
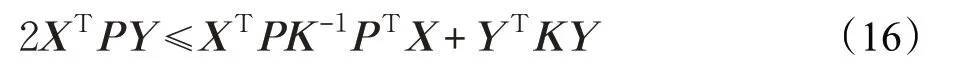
引理3[26](schur 补定理)对于给定的对称矩阵S=,以下三个条件是等价的:
(1)S <0。
(2)S11<0,S22-
(3)S22<0,S11-。
引理4[27]设函数y(t)在t ∈[-τ,∞)是连续非负的,且满足下列条件:
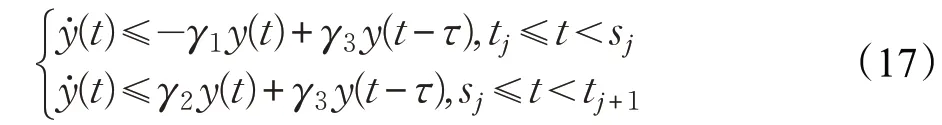
其中,γ1,γ2,γ3均为正常数,j=0,1,2,…,若:

证明参照文献[27]。
设计控制器使系统达到稳定状态,首先,将所设计的动态反馈控制器式(8)作用于系统(2),得到如下闭环系统:
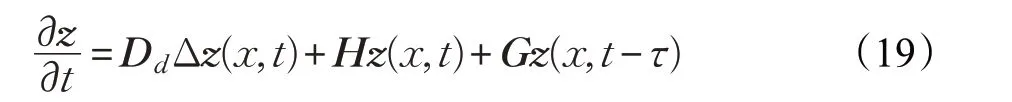
其中:
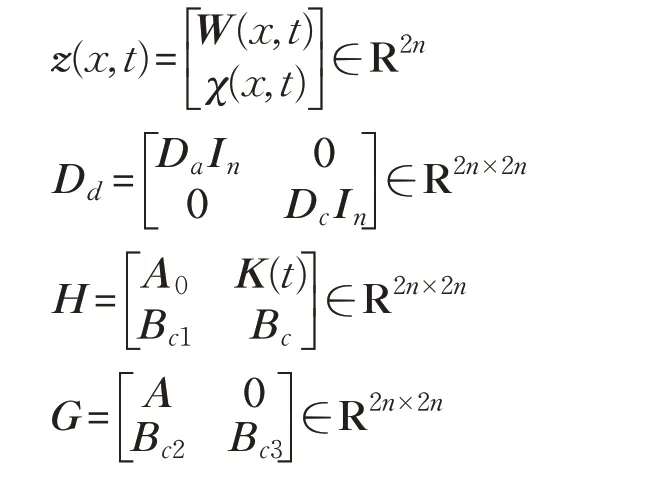
注2 针对分布参数系统,中和控制的行为过程在时间及空间位置上是一个自发的控制过程,在每个空间位置节点上,其控制不一定是持续连续的,控制周期可能是以一种不连续的间歇控制方式实现的,而对于所有节点,其间歇控制特性又不尽相同,所以本文在此基础上,对中和控制方案进行改进,将中和控制方法与非周期间歇控制方案结合,对于系统所有节点,考虑控制周期不尽相同,同时利用假设条件1,得到系统稳定的充分条件。
定理在给定参数条件下,当存在正常数a1,a2,矩阵W ∈Rn×n为正定对称矩阵,矩阵M,X1,X2,X3,X4,X5∈Rn×n满足下面矩阵不等式:
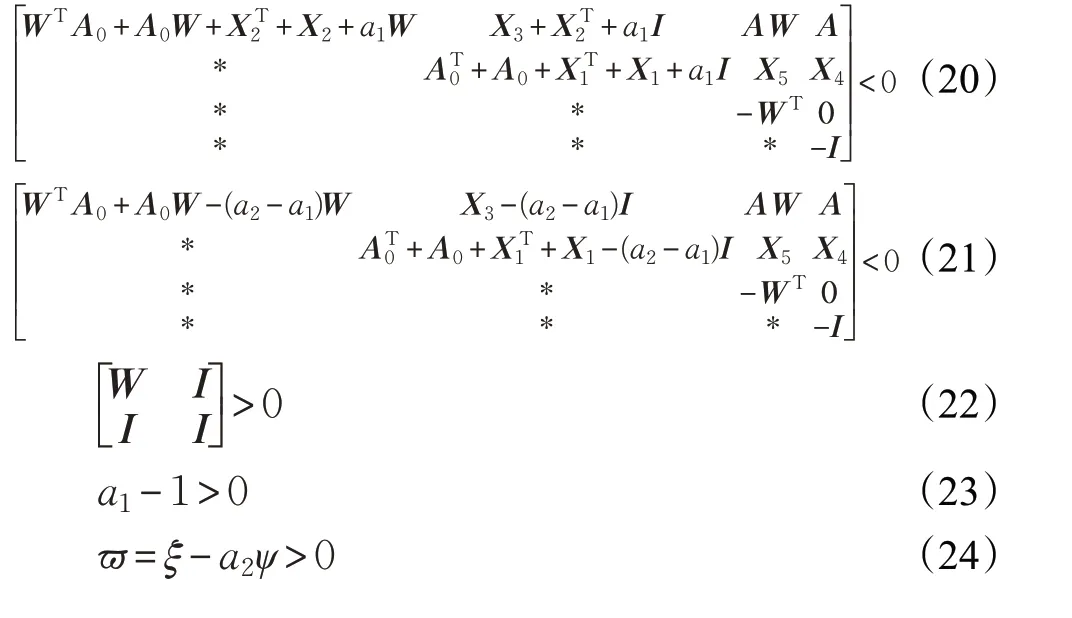
其中,X1=Bc1,X2=KMT,X3=WTAT0+WTX1T+MBTc+A0,X4=A+Bc2,X5=X4W+Bc3MT,ξ >0 是方程ξ-a1+exp(ξτ)=0 的唯一正解,则所构建的动态反馈控制器使系统镇定。
证明构造李雅普诺夫函数为:
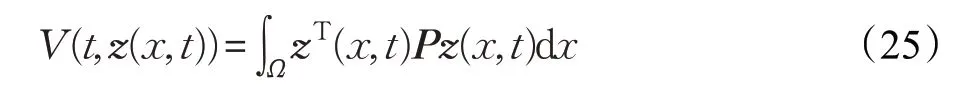
当t ∈[ )tj,sj时,有:

对于∫ΩχT(x,t)Δχ(x,t)dx 同理可得:
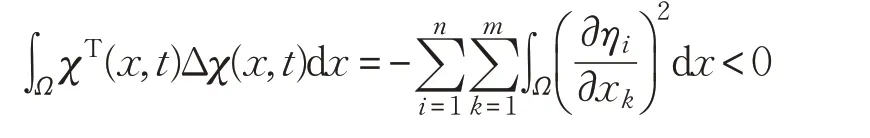
其中,PDd≤λPDmax,对于D >0,Dc>0,P >0,所以λPDmax>0,所以得:
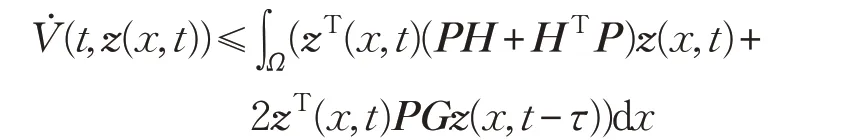
由引理1,可得:
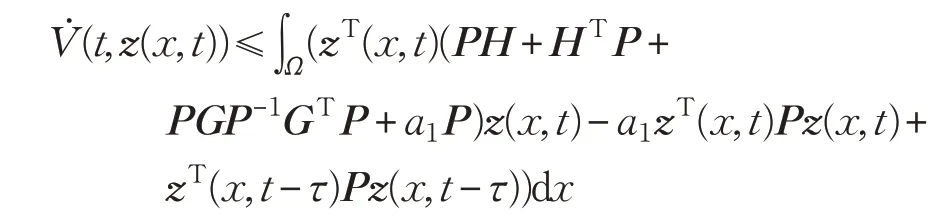
若
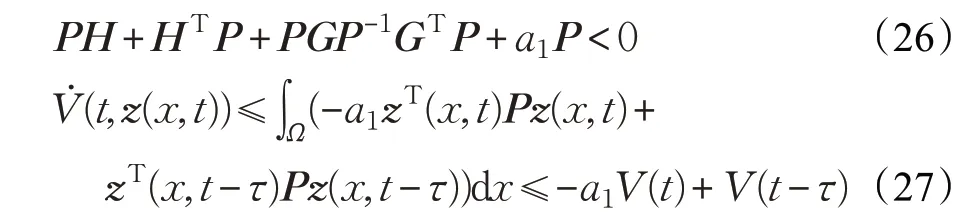
对式(26)根据引理2(schur补定理),可得:
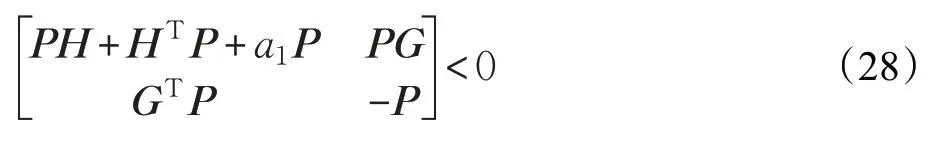
由矩阵不等式(28)求解控制器时,控制器参数K,Bc,Bc1,Bc2包含在矩阵H 和矩阵G 中不能被求出,所以接下来的目的是求解控制器参数。
首先,将矩阵P,S 分区,定义:

其中,W 是正定对称矩阵,M ∈Rn×n是可逆矩阵,且PP-1=I,

定义两个矩阵:
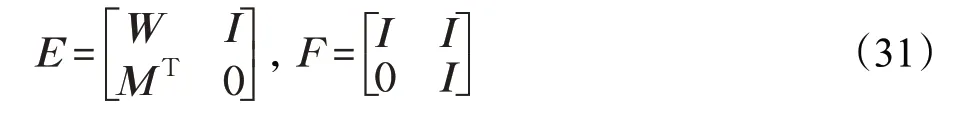
有:

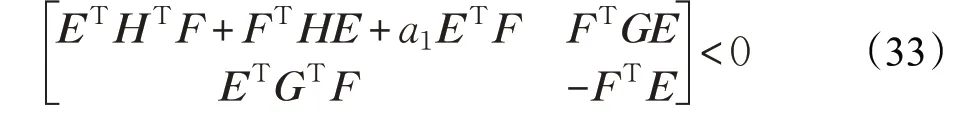
由式(29)~(33),根据Schur 补定理,可得在定理1条件(20)(22)情况下,式(27)成立。
当t ∈[ sj,tj+1)时,有:
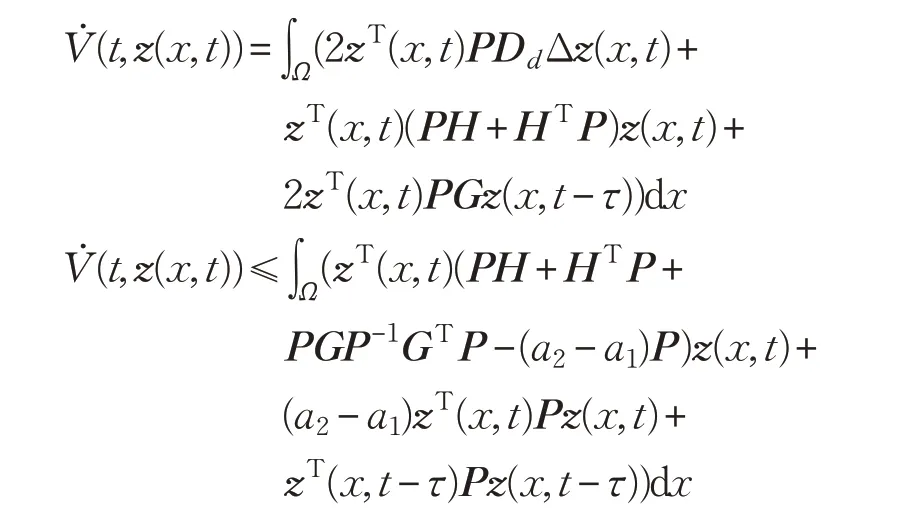
若:
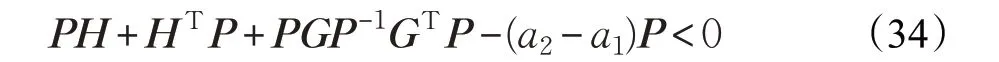
则:
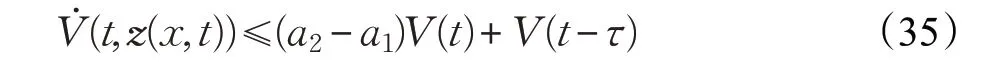
对于式(34),同理可得在定理1条件(21)(22)情况下,式(35)成立。
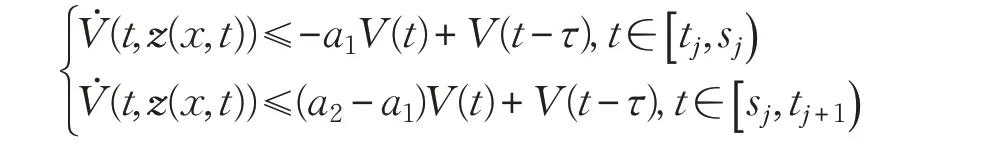
根据引理4:
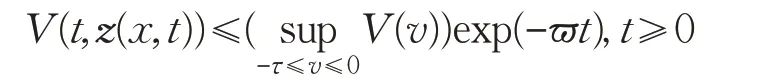
由此,定理1得证。
推论在给定参数条件下,考虑系统时滞τ=0,当存在正常数a1,a2,矩阵W ∈Rn×n为正定对称矩阵,矩阵M,X1,X2,X3,X4,X5∈Rn×n满足下面矩阵不等式:
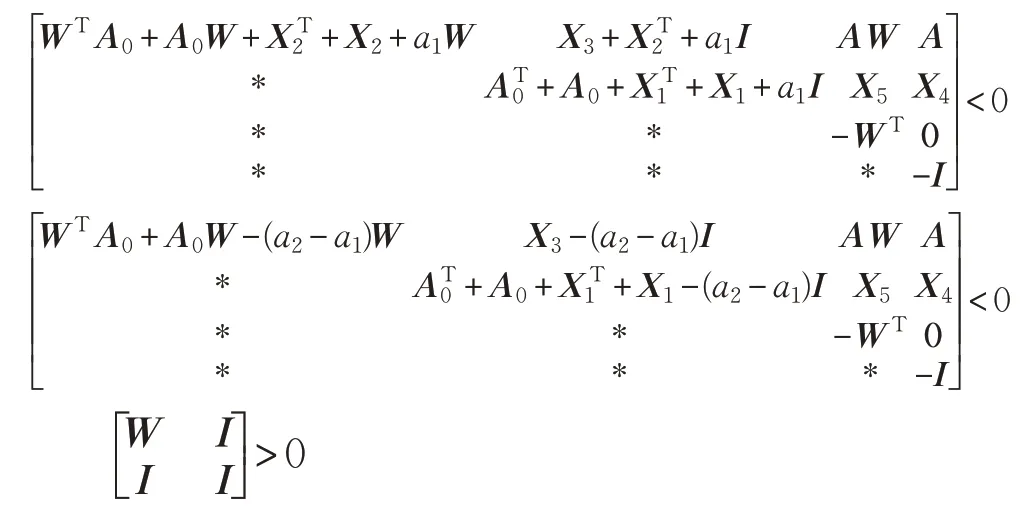
a1-1 >0,ϖ=ξ-a2ψ >0,其中:
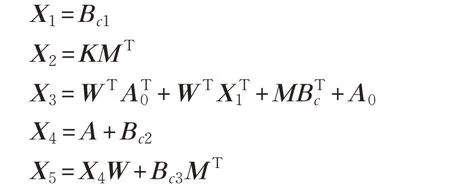
ξ >0 是方程ξ-a1+exp(ξτ)=0 的唯一正解,则所构建的动态反馈控制器使系统镇定。
证明参考定理证明。
3 数值仿真
为了说明问题,考虑如下分布参数系统及控制系统:
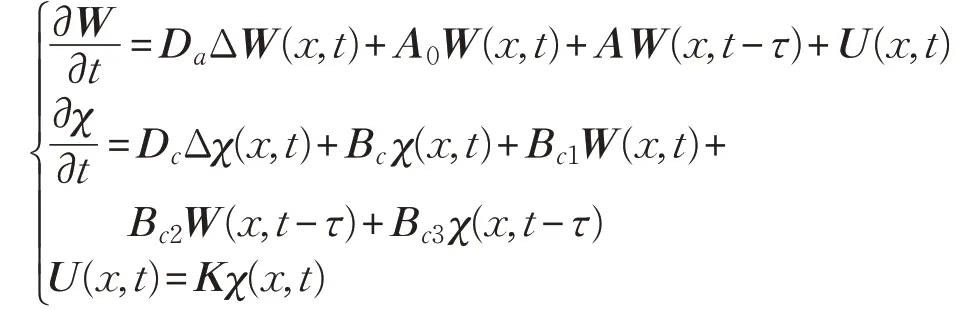
对分布参数系统,取m=1,n=2,系统参数Da=;
取时滞τ=0.2,应用定理1 所提出的方法,选取ξ=1.22 ,取a1=2.5 ,a2=3,得出对于所有节点的添加间歇控制器,控制宽度为0.6,取,通过Matlab 软件中的LMI 工具箱,可以得到控制系统参数:

给定系统的初始条件:
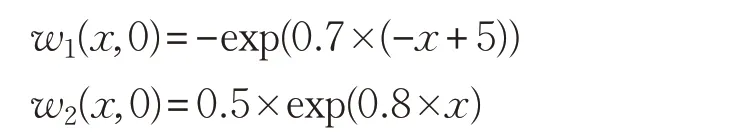
η1(x,0)=0,η2(x,0)=0,图2、3 分别给出了系统状态和控制系统的状态图。
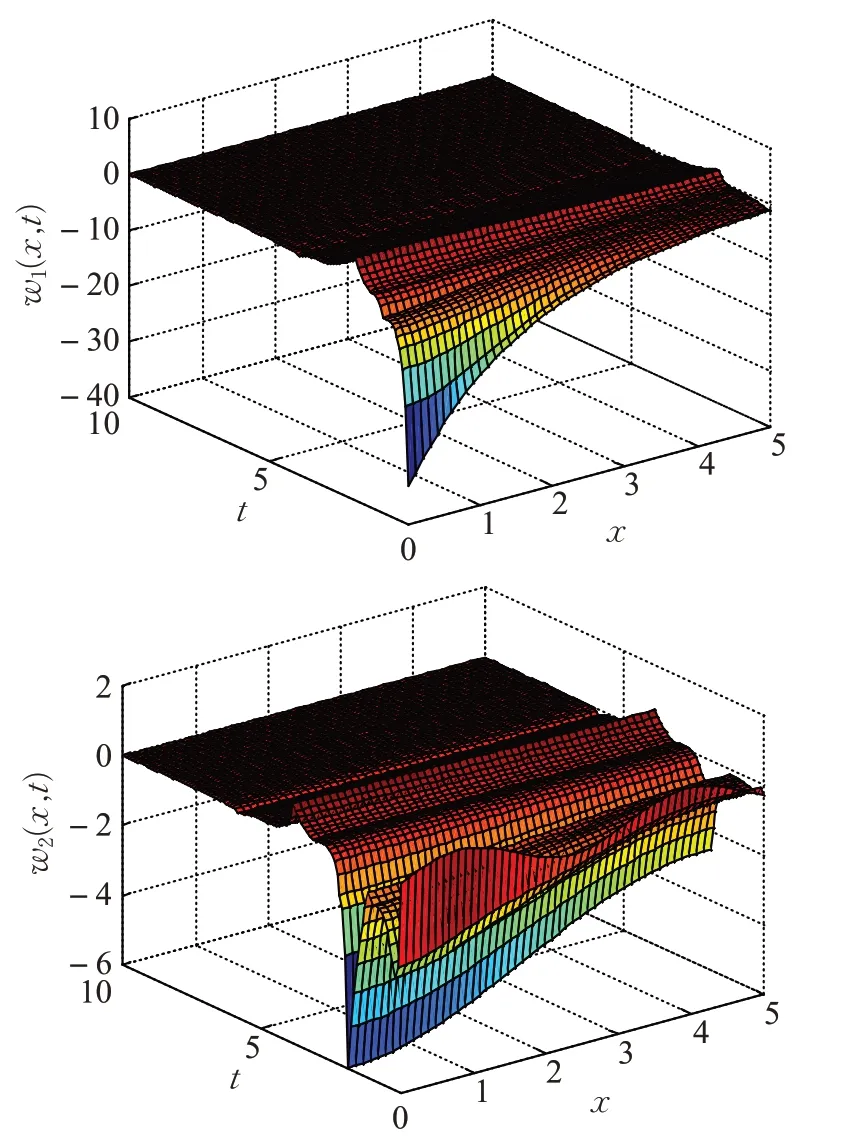
图2 系统状态W(x,t)图
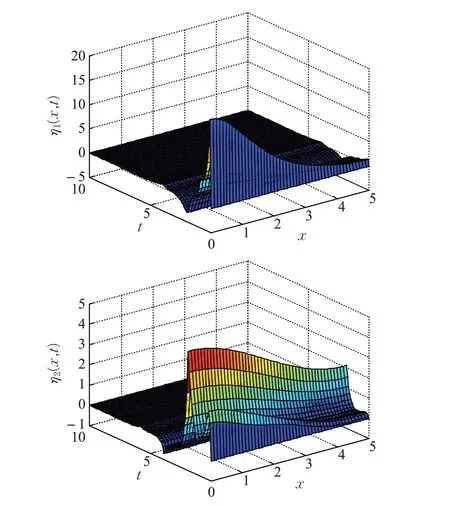
图3 控制系统状态χ(x,t)图
4 小结
本文针对时滞分布参数系统,研究其稳定性问题。首先结合中和控制器及非周期间歇控制器设计思路,得出了一种全新的控制方案——非周期中和控制器,不仅弥补了中和控制器的不足,更使其应用范围得到提升。利用Lyapunov 稳定性理论并结合LMI 处理方法,得出了具有时滞特性分布式参数系统稳定非周期间歇中和控制器存在的充分条件。最后结合所给条件,给出一个数值仿真说明其有效性。

