基于残差网络的图像超分辨率重建算法

陈 晨，刘明明，刘 兵，3，周 勇

1.中国矿业大学 计算机科学与技术学院，江苏 徐州221116

2.江苏建筑职业技术学院 智能制造学院，江苏 徐州221008

3.中国科学院 航空航天信息研究所，江苏 徐州221116

1 引言

本文所要研究的超分辨率图像重建（Super Resolution Image Reconstruction，SRIR 或SR）是一种图像复原的方法，是指通过软件算法的方法，将低分辨率（Low-Resolution，LR）的图像或者序列转化为高分辨率（High-Resolution，HR）的图像[1]。实际生活中，自从有了照相机、摄像头，通过不断的改进向世界呈现真实画面就成为了人们不断研究的目标，此项图像超分辨率重建技术更多的是用来实现对目标物体专注度的分析，来获得人们感兴趣的更高的空间分辨率的图像，而不需要直接采取数据量极大的高空间分辨率图像的配置。用时间带宽换取空间分辨率，实现时间分辨率和空间分辨率之间的转换是超分辨率重建的核心思想。

Harris和Goodman等在1969年时，通过将带限信号外推的方法来解决了当时的光学图像超分辨率重建的问题，在此确定了图像超分辨率重建的数学基础[2-3]。1984 年，Huangi 和Tsa 等提出了频率域法，核心思想是利用图像之间傅里叶变换的位移性质，将单幅图像超分辨率重建扩展到多幅图像超分辨率重建，将高低分辨率之间的位移关系通过傅里叶变换来建立，开启了多幅图像超分辨率重建的新篇章[4]。后来，Freeman等在2002年时利用马尔可夫网络提出了一种新的基于样例学习的图像超分辨率重建算法，通过训练图像建立一个数据库，学习高低分辨率图像和领域高分辨率图像的关系来重建出新的高分辨率图像[5]。截至目前，通过多位学者的研究可将图像重建算法分为以下三大类：基于插值、基于重构、基于学习。

为了提高图像超分辨率重建的效果，Yang[5]等人提出了基于稀疏表示的图像超分辨率重建，此算法的核心内容是通过联合训练两个用于高低分辨率图像块的字典，这种办法可以有效增强高低分辨率图像块对相对于自身字典的稀疏表示的相似性。在这个前提下，低分辨率的图像块的稀疏表示和高分辨率图像块的字典产生高分辨率图像块，这样可以有效地降低算法的计算成本。传统的凸集投影（POCS）算法能够重建低分辨率（LR）图像，但在保留图像细节和去噪方面存在矛盾，从而限制了重建图像的质量。为了避免POCS的缺陷，获得更高的分辨率，Shang 等人[6]将基于稀疏表示的思想用于图像的去噪。稀疏表示对图像的数据具有自适应性，能够学习优化图像过完备稀疏字典，用来描述图像的本质特征，来达到有效的去噪目的。2016 年，Dong等[7]率先提出基于卷积神经网络（SRCNN）的方法，核心思想是使用三个卷积层，将图像特征在低分辨率空间和高分辨率空间建立非线性映射，实验结果表明此方法的重建效果优于其他传统方法。

之后，Kim[8]等人受ResNet 的启发，在SRCNN 的基础上提出了超深卷积神经网络图像超分辨率重建，引入了20 层卷积层和全局残差学习，得到了非常好的重建效果，但内存占用较大且计算复杂度较高。

同年，RED 网络结构被提出，主要特点在于此网络引入了反卷积层，卷积层与反卷积层一一对应，反卷积层恢复因经过卷积层而减小的图像尺寸，能够有效地恢复图像细节。采取30 层网络结构，相对应的卷积层与反卷积层跳跃相连，将反向传播信号直接传递到底层，避免梯度消失的同时有效地重建出高质量的图像。

近几年随着医疗事业的发展，研究者逐渐开始研究磁共振图像的重建。刘振圻等[9]于2013 年将重建技术与现有的去噪技术相结合，在重建图像的同时，达到去噪的效果，有效地提高了磁共振图像的分辨率。

近几年，许多方法[10-15]在图像超分辨率重建方向都取得了不错的效果。稀疏分解先于压缩感知提出，信号稀疏表示是为了在给定的超完备字典中尽可能用少量的原子来表示信号，因此来获得简洁的信号表示方式，可以更加容易地从信号中获取所要蕴含的信息，方便对信号进行进一步加工处理。

2 相关工作

2.1 卷积神经网络

卷积神经网络（Convolutional Neural Networks，CNN）是一类包含卷积或相关计算且具有深度结构的前馈神经网络（Feedforward Neural Networks），是深度学习（deep learning）的代表算法之一[16-17]。在卷积神经网络中每一个节点代表的都是一个神经元，这点和全连接神经网络一样。

卷积层计算公式如下：

其中，ylj表示的是第l 层卷积层中第j 个卷积核的输出，通常情况下称作特征图，它代表的是一个二维向量；代表卷积核，表示的是第l 层卷积层输入的第i 个特征图与第l-1 层输出的第j 个特征图之间的卷积核；blj表示的是第l 层卷积层的第j 个卷积核的偏置项；Mj表示的是所有特征图集合，代表的是输入特征图要连接到输出的第j 个特征图，将卷积操作的符号表示为⊗。

特征提取是卷积神经网络与传统神经网络之间最大的区别，卷积层和子采样层构成了特征提取部分，卷积层中，神经元之间并不是完全连接，其中，一个神经元只与部分邻层神经元连接。

从低分辨率图像中有重叠的提取图像块并用高维向量表示，相当于采用一组滤波器对图像进行卷积操作，图像重建阶段是将重叠的高分辨率图像块进行平均化操作产生最终的高分辨率图像，而非线性映射阶段是将上一层的特征向量从低分辨率空间变换至高分辨率空间。

2.2 基于卷积神经网络的图像超分辨率重建（SRCNN）

首次将深度学习应用到图像超分辨率重建中，SRCNN直接学习的是高低分辨率图像之间的端对端映射。映射表现为一个深度卷积神经网络（CNN）[14]，输入的是低分辨率图像，输出的是高分辨率图像，如图1。SRCNN不像传统的稀疏表示的图像超分辨率重建分开处理每个部件，此共同优化了所有的层，有很好的重建质量，在实际应用中也取得了很好的效果。

SRCNN首先做的预处理是使用双立方插值的方法来提升到它所需要的尺寸记作Y ，这是SRCNN中唯一执行的预处理，图像超分辨率重建的目标是将Y 恢复为重建后的图像F(Y),F(Y)与原始的真实的高分辨率图像X 需要尽可能地相似，网络结构中学习到的映射记作F,F 从概念上由小块的提取和表示、非线性映射、重建这三个操作组成。分成以下三个操作：

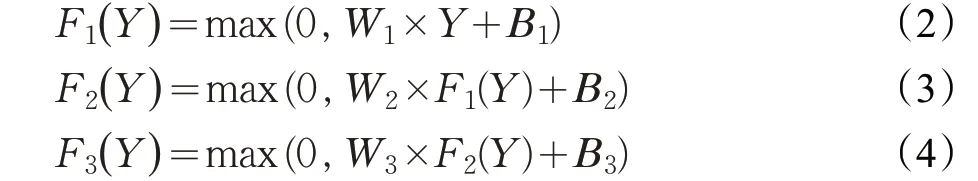
其中，W1代表滤波器，而B1代表偏置，将W1的大小定义为c×f1×f1×n1。输入图像中通道的数量记作c，滤波器的空间大小记作f1，滤波器的数量记作n1。通俗来讲就是，滤波器W1在图像上进行n1次的卷积操作，输出图像由n1个特征图组成。 B1表示的是n1维的向量，B1的每个元素都与一个滤波器相对应。本文采用ReLU函数(max(0,x))[18]在滤波器响应上。W2、B2、W3、B3同理。

SRCNN有它独特的优点。首先，SRCNN的网络结构非常简单，和基于样本的图像超分辨率重建方法相比，有着相同的优秀的精准性。其次，这个方法因为中等数量的过滤器和层数，所以在实际在线使用中甚至是CPU 上，也实现了很快的速度。由于SRCNN 是完全前馈的，因此在训练速度方面比基于样本的方法要快一点，且不需要解决优化问题。最后，当数据变多，或者使用模型变大的时候，通过实验证明是可以达到进一步的改善网络的修复质量的目的。

2.3 残差网络（ResNet）

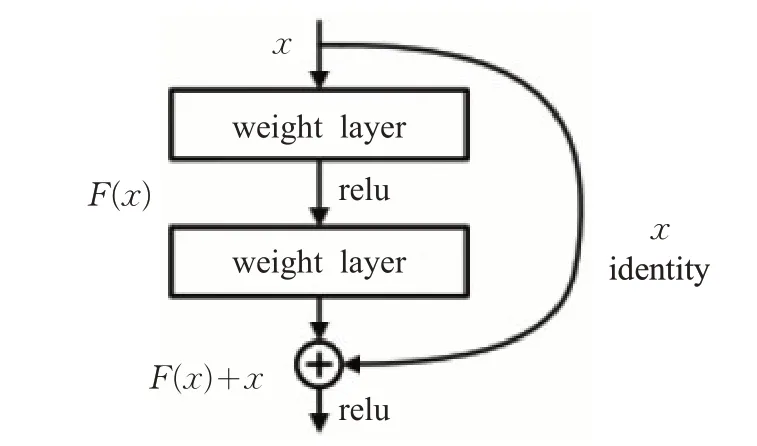
图2 ResNet结构简图

网络结构的基本要求：（1）输出特征映射大小相同的网络层需要有相同数量的过滤器，即通道数相同；（2）当特征映射大小减半时（经过池化层），通道数量翻倍。

残差单元的结构表示为：

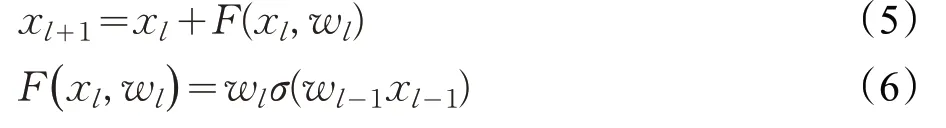
σ 为激活函数，C 为损失函数：

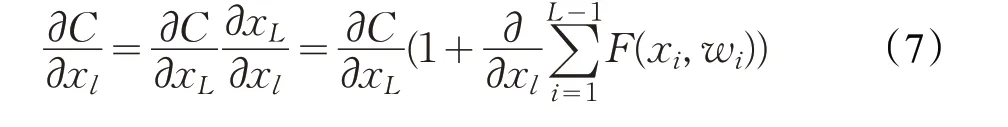
2.4 Very Deep Convolutional Networks（VDSR）

残差结构被运用到大量的实际运用中，在图像超分辨率重建领域，表现最直观的模型是VDSR，在2016 年时提出，通过残差网络来解决加深网络而导致的梯度问题[8]。

VDSR将网络结构加深到20层，实验验证在图像超分辨率重建上达到了很好的效果，采取了残差学习来提高学习率，防止因为网络结构太深对梯度传输产生障碍。并且为了防止卷积使得图像越来越小，在下一次卷积前，对图像进行补0 操作。VDSR 的第三点特别之处在于将不同大小倍数的图像混合在一起训练，这样训练出来的一个模型就可以解决不同倍数的超分辨率问题。

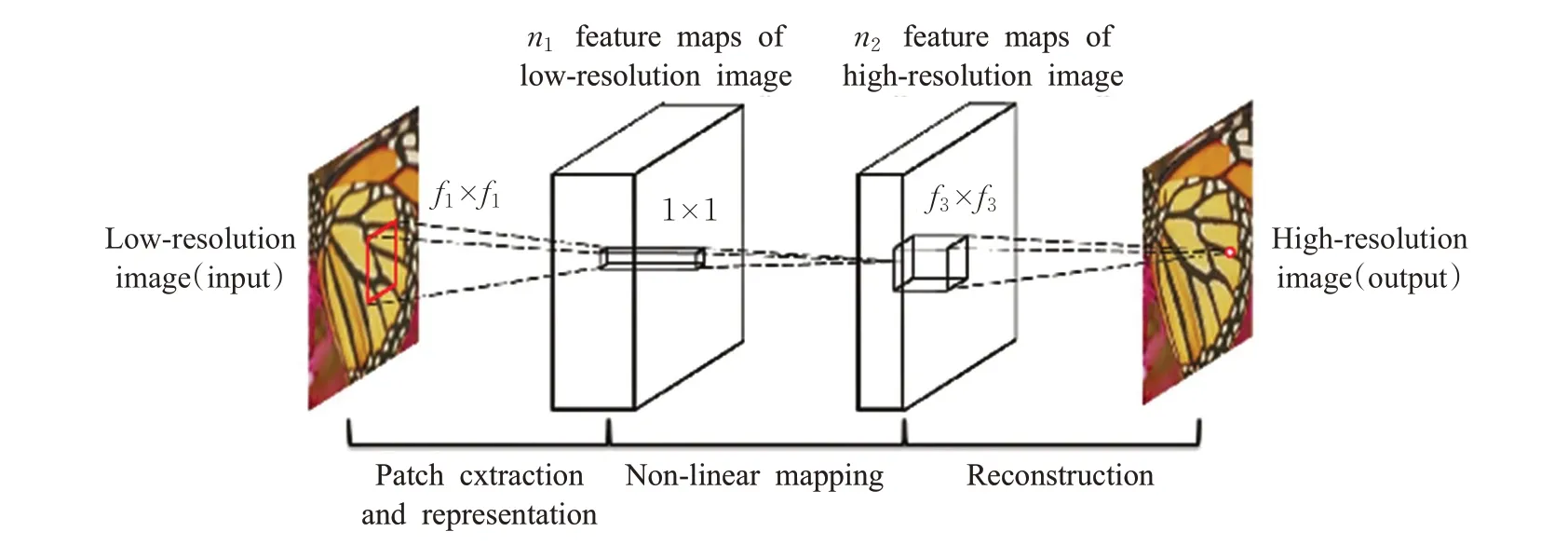
图1 SRCNN网络结构图

3 模型设计及算法流程

为了有效提高图像超分辨率重建的效果，本文在原始SRCNN 的基础上加深了网络结构，但是伴随着网络结构的增加，网络负重也增加，因此为了解决这个问题提出了本文的网络模型。

3.1 模型设计

在本节中，将详细介绍本文所设计的ResNet 和SRCNN相结合的图像超分辨率重建模型。在VDSR及其他典型深度学习的图像超分辨率重建算法中，皆有提及图像重建的效果随着网络层次的加深而提高，加深网络结构虽然会得到不错的效果，但随着深度到达一定的程度时，继续增加深度会导致网络模型误差变大的现象发生。本文主要采用残差学习来减少网络的负重，简单来说，网络不需要去记忆太多的信息，相较于非残差模式，非残差模式随着网络层数的增多，需要记录的特征也随之增多，对于位于深层次的卷积层而言，一些图像信息特征已经丢失（这是由于网络负载过大造成），因此可以采用残差学习一定程度上缓解这个问题。

残差学习的目的类似于ResNet 结构模型中的残差学习单元。输入低分辨率图像x，网络模型表示为y，当传统卷积神经网络到达一定的深度时，可以使得逼近y，此时继续增加网络模型的深度可能会造成饱和目标函数的偏移，因此在RDSR-a模型中，采用残差学的方法将学习目标转换成y-x，使得模型达到继续优化的效果。在网络模型中加入递归学习的方法，为了达到不增加参数的效果，递归层的卷积层之间权值共享，从而提高学习率。

如图3 所示，是简化的网络模型，采取局部残差学习和全局残差学习相结合的方法，所提出的网络模型可以解释成五个步骤：特征提取、收缩、非线性映射、扩张、最后的重建。

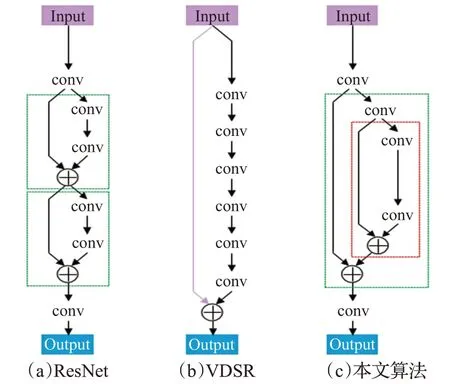
图3 简化的网络模型

第一部分是特征提取阶段，传统SRCNN 仅有三层卷积层，感受野较低，为了增加感受野，采用加深网络结构的方法。随着网络结构的加深，感受野逐步变大，感受野越大表示其能接触到的原始图像范围就越大，可以根据更多的像素点去推断结果像素点。但是随之而来的是运算复杂度的提升，因此，第二部分是应用1×1 的卷积核进行降维，减少网络参数，降低算法的复杂度。第三部分非线性映射部分考虑到加深的网络结构可能会造成学习速率降低，或者梯度爆炸、梯度消失的问题，采取残差学习的方法提高学习率，并且对梯度进行裁剪，提高学习率。

可以通过残差学习提高学习率的方法来解决网络层次加深带来的梯度消失的问题，梯度爆炸和梯度消失的原因可以理解为信息流的过大或者过小，产生这个问题的原因在于网络的负载过大。在深度网络中，图3（c）红色部分即为此网络结构的深度部分。实验部分最先采用6 层卷积层，重建效果并不明显，因此本文采用16层卷积。此外，残差学习在一定程度上加快了算法的收敛速度。

第四部分应用1×1的卷积核扩维到原始维度，最后反卷积重建，实现上采样操作，回复原始图像大小，达到重建后的图像和原始尺寸相同。

算法描述：

输入：低分辨率图像

输出：高分辨率图像

步骤1 选取3×3 的卷积核对低分辨率图像进行特征提取；

步骤2 选取1×1的卷积核进行降维，减少网络参数；

步骤3 进入图3（c）网络结构ResNet 结构中进行训练；

步骤4 应用1×1的卷积核扩维；

步骤5 进入反卷积层，上采样到原始目标图像尺寸；

步骤6 重建出最终的高分辨率图像。

3.2 损失函数

考虑到传统基于卷积神经网络的图像超分辨率重建的图片通过逐步卷积会导致图片越来越小，不适合一个很深的网络。减少SRCNN 中双三次插值的预处理，将原始图像的尺寸作为输入，直接进行卷积操作。考虑到当采用传统卷积操作时，感受野小，边缘区域考虑得较少，于是采取对卷积结果做裁剪的方法，剪去边界区域，但是会使得图像变得更小，因此下一次卷积前，对图像进行补0，将重建图像恢复到原始图像的大小，这样不仅解决了深度浅的问题，也加深了对图像边缘的操作，通过实验证明了对图像细节处理确实是有了明显的改进。

损失函数延用SRCNN中的均方误差（MSE）：

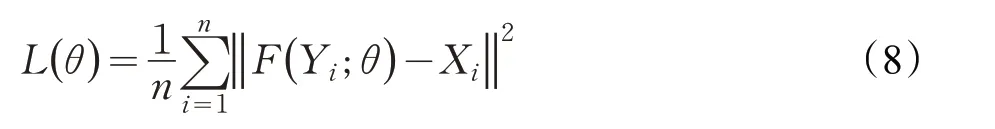
其中，n 表示的是训练样本的数量。使用具有标准反向传播的随机梯度下降法使损失最小化[19]。如果只有损失函数可推导，CNN 并不排除使用其他类型的损失函数。如果在训练过程中给出更好的感知度量，它能够灵活地针对网络去适应度量。相反，这样的灵活性通常来说对于传统的“手工”方法是很难实现的。

3.3 反卷积重建

在实际实验中，卷积操作会使图像越来越小，考虑到这个影响，采取反卷积操作对图像进行重建，能够多尺度放大特征映射图。并没有像SRCNN采用双三次插值预处理是由于双三次插值的预处理限制了学习速度[20-21]。反卷积（Deconvolution）的概念第一次出现是Zeiler在2010年发表的论文《Deconvolutional networks》中，但是并没有指定反卷积这个名字，反卷积这个术语正式的使用是在其之后的工作中[22]。通过反卷积可以使图像变大，实现图像的上采样效果得到想要的图像大小，反卷积的反向传播即卷积层的前向传播，卷积层的前向传播为乘以C，反卷积层的反向传播为乘以(CT)T。

4 实验结果分析

本文所有程序在tensorflow 环境spyder 编译器下运行，硬件平台为PC：Inter®CoreTMi7-8750H CPU@2.20 GHz，内存为8 GB。交叉验证法采用传统的留出法，将数据集分为训练集、验证集和测试集三部分。

在实验中，训练此次改进的残差卷积神经网络的图像集为常用的91 幅自然图像，采取与VDSR 算法中相同的缩放、旋转的方式进行样本增强。

并且同样运用Set5 和Set14、Urban100 测试集对残差网络进行测试。这三个数据集为图像超分辨率重建常用数据集，Set5数据集包含动植物图像，Set14包含动植物、景物图像，细节信息比Set5更多，Urban100数据集包含的是城市建筑图像，边缘信息多，重构难度大。

4.1 评价指标

本文采取的衡量标准是图像超分辨率中常用的评价指标：峰值信噪比（Peak Signal to Noise Ratio，PSNR）和图像的结构相似性（Structural Similarity，SSIM）。

通常来讲，更高的PSNR 表示了更高分辨率的图像，一般情况下通过均方误差（Mean Square Error，MSE）进行定义：

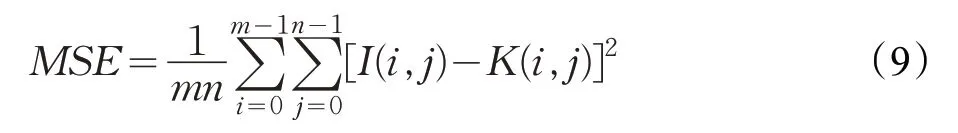
峰值信噪比（PSNR）表示为：

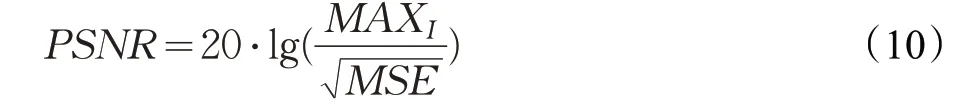
其中，I 和K 表示两个m×n 大小的图像。规定PSNR的单位是dB，且数值越小表示失真越大，即数值越大失真越小。

结构相似性（SSIM）表示为：

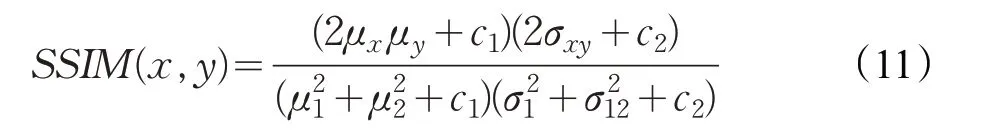
其中，μx表示x 的平均值，μy表示y 的平均值，σx表示x 的方差，σy表示y 的方差，σxy表示x 和y 的协方差。且规定结构相似性的范围是-1 到+1（即SSIM ∈(-1,0]）。

4.2 在数据集上的对比

本文算法主要从加深网络结构、降低网络复杂度方向进行研究。图4 表示在Set5 测试集上本文提出的超分辨率重建算法和其他算法的对比，Set5中的蝴蝶图像在放大细节后可以观察到，本文算法的重建效果更好，细节纹理更加清晰。图5是在Set14测试集上本文提出的超分辨率重建算法和其他算法的对比，Set14 中人像图像在放大帽子边缘的细节后可以看出，本文重建算法的纹理与Bicubic重建的图像和SRCNN、VDSR重建的图像对比均更加清晰。图6是在Urban100测试集上本文提出的超分辨率重建算法和其他算法的对比，Urban100 中图像在放大左上角的细节后可以看出，本文重建算法的纹理与Bicubic、SRCNN、VDSR重建的图像对比均更加清晰。因此，本文提出的增加网络层数引进残差网络的图像超分辨率重建效果从视觉效果来说是有所改进的。

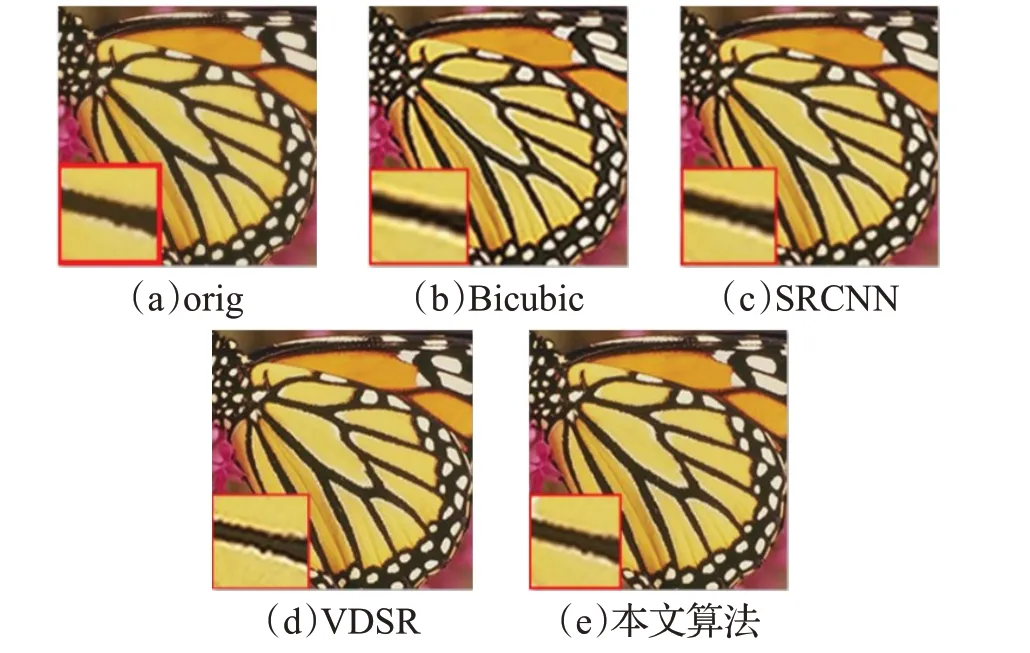
图4 Set5测试集上的对比

图5 Set14测试集上的对比

图6 Urban100测试集上的对比

表1 表示了本文方法和Bicubic、SRCNN、VDSR 在两个数据集上且上采样因子分别为2、3、4时的对比，可以看出Bicubic、SRCNN、VDSR 三种方法在scale 值为2时PSNR和SSIM的值最大。由于本文采取反卷积扩大尺寸，预处理中并未做上采样操作，所以本文结果与其他三种方法最好的情况进行对比。本文算法的PSNR与SSIM 值为采取八组实验后的平均值。Set5 中，本文算法的PSNR 值比VDSR 提高0.07 dB，比SRCNN 提高0.29 dB，比Bicubic提高3.92 dB，本文算法的SSIM值比VDSR提高0.01。Set14中，PSNR值最高的是VDSR，可以看出本文的33.79 dB 比VDSR 的33.03 dB 提高了0.76 dB，本文算法的SSIM 值为0.91 也比SSIM 值为0.90的VDSR和SRCNN算法要高。Urban100中，PSNR值最高的是VDSR，可以看出本文的31.01 dB 比VDSR的30.77 dB 提高了0.24 dB，本文算法的SSIM 值为0.92也比SSIM值为0.91的VDSR算法高。因此可以得出本文算法在数据上优于其他算法的结论。

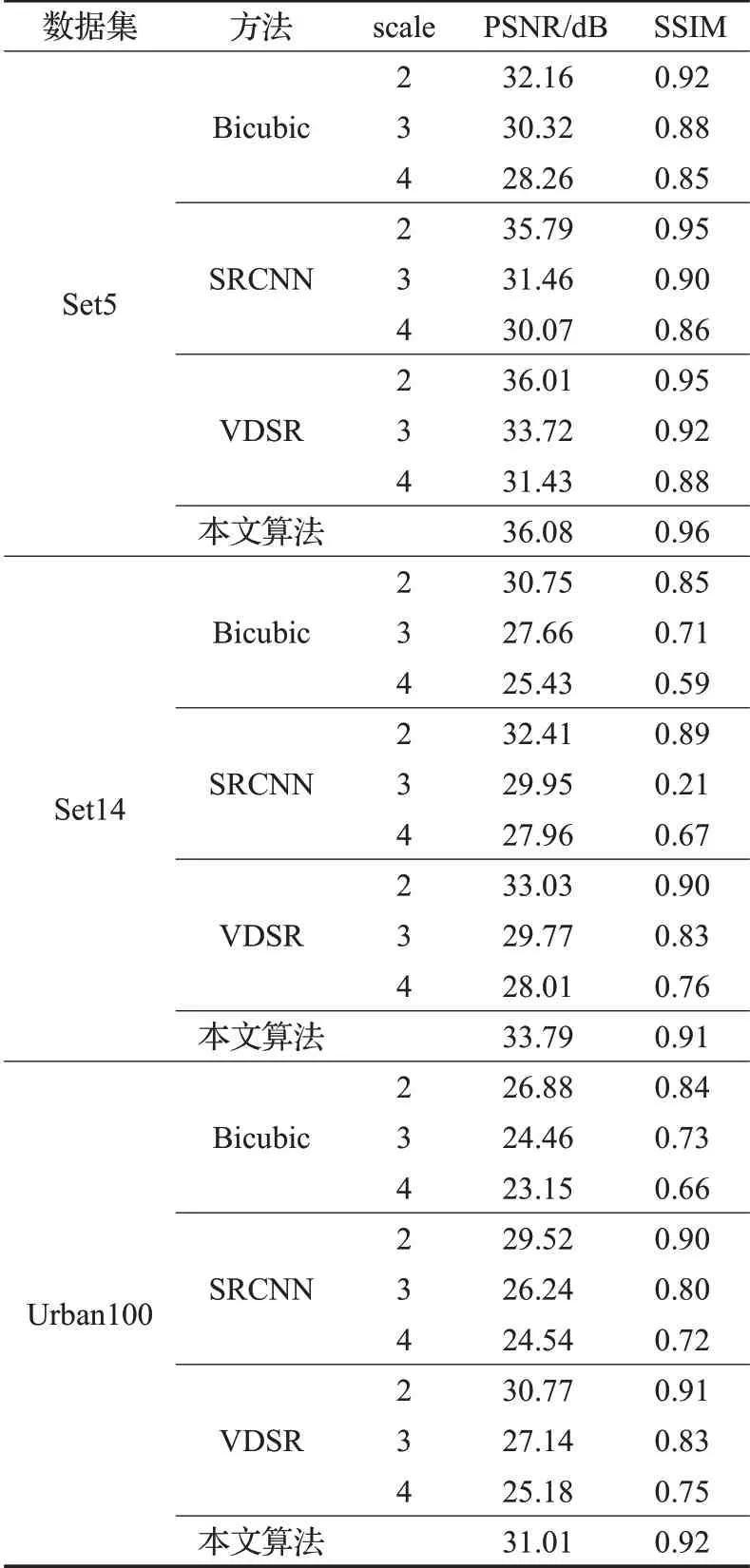
表1 各方法在不同数据集下的PSNR、SSIM值对比

4.3 消融法

本文主要从网络深度和网络结构两个方面对原有的SRCNN算法进行改进，提出了两点改进[23]：

（1）采取局部残差和全局残差相结合。

（2）取消双三次插值，在最后增加反卷积层，且在残差网络结构首尾分别加入1×1的卷积核进行降维和扩维。

随着网络结构的加深，必然会带来算法复杂度的提高，采取1×1卷积核降维可以在不增加参数的情况下降低算法复杂度，有效地提高算法效率，尾部1×1 扩维到原始维度。

为了验证对残差网络进行降维和扩维的有效性，本文采取消融法，对进行降维和扩维的算法验证，采取同样的Set5、Set14、Urban100 数据集，训练集也采取相同的训练集，进行同样的缩放操作。采取八组实验取平均值，在Set5上的PSNR和SSIM值分别为36.03 dB和0.95，在Set14 上的PSNR 和SSIM 值分别为33.41 dB 和0.91。在Urban100 上 的PSNR 和SSIM 值 分 别 为30.89 dB 和0.91。与本文提出的方法对比，本文算法的PSNR 值分别高了0.05 dB、0.38 dB、0.12 dB，而SSIM 值在数据集Set5、Urban100上也提升了0.01。

因此，从客观评价指标中，可以得出本文算法的有效性。和SRCNN、VDSR算法相比，本文算法在主观和客观评价指标上有所提升。

5 结语

SRCNN 的训练速度较慢且存在网络深度的问题，针对这一缺点，本文提出加深卷积层深度，且为了避免深度太深无法训练加入了残差网络ResNet，减少了SRCNN 中Bicubic 步骤，在训练时只fine-tuning 最后的反卷积层，提高了训练速度。引入了全局模式的残差学习和局部模式的残差学习相结合的方式来降低在深层网络中由于网络加深造成的训练难度，并且使用由残差单元组成的递归块来学习高分辨率和低分辨率图像之间的残差图像，可以通过增加网络深度来提高精度，而不需要添加任何权重参数。该算法能够更好地重建图像的高频纹理信息，不论是客观评价还是视觉效果上都取得了较好的效果[24]。

对于未来的研究方向，观察到此次的算法主要对网络结构进行改进，有一定的改进效果，但是距离更好的优化还有一定的改进空间，因此在接下来的研究工作中，将考虑到改进现有的其他算法，例如GAN 网络，并考虑图像超分辨率重建在实际运用中的实验，例如医学图像、光学遥感图像中的运用等[25]。