基于目标预测的扩展目标量测集划分算法

王文慧，李 鹏，胡韵迪

1.江苏理工学院 艺术设计学院，江苏 常州213001

2.江苏理工学院 计算机工程学院，江苏 常州213001

1 引言

传统目标跟踪认为，一个目标在传感器上显示为一个点。但随着传感器技术不断进步，一个目标可能在激光雷达、船舶雷达等高精度传感系统中显示为多个点，称这种目标为扩展目标。扩展目标跟踪研究在车辆跟踪、航船监视、机器人视觉、定位导航等领域有着巨大的应用价值，因此成为近年来各学者研究的热点。

针对扩展目标跟踪问题，Mahler教授提出扩展目标PHD跟踪算法[1]，为随机有限集（Random Finite Set，RFS）理论在扩展目标跟踪领域的应用提供了理论指导，然而该算法由于似然函数求解困难，并未给出具体的程序实现方案。Granström 等人对上述理论框架进行程序实现，分别提出了ET-GM-PHD[2]和GIW-PHD[3-5]两种不同的算法，可以有效地实现不同情况下多扩展目标的精准跟踪，并且国内外众多学者对上述两种算法进行了一定的改进[6-8]。ET-GM-PHD算法适合在传感器两侧噪声已知的情景下使用，具有运算速度快的优势，然而在目标邻近时性能下降。造成该情况的原因是量测集划分算法不能有效地划分邻近目标的量测集。

针对ET-GM-PHD 算法的量测集划分问题，Granström 等人提出了一种基于子划分思想的划分算法，即DP-Kmeans++划分算法[9]，首先利用距离划分DP算法进行初步划分，然后利用Kmeans++算法[10-11]将可能包含多个目标集合进行子划分，提高了目标邻近时的划分效果。然而，ET-GM-PHD 算法在目标邻近时的性能依然不足，因此众多学者对扩展目标划分问题展开研究[12-14]。但这些研究成果仅降低了运算时间代价，其划分精度依然有待进一步提高。

针对扩展目标的量测集划分的精度问题，本文提出一种DP-Kmeans++的改进算法，称之为DP-TP-Kmeans++算法。在原算法运用的DP和Kmeans++步骤之中，插入一步基于目标预测（Targets'Prediction，TP）的量测集分割步骤，进一步提高了邻近目标的划分精度。仿真结果表明，提出算法的OSPA误差距离明显小于其他量测集划分算法。

2 扩展目标高斯混合滤波概述

2.1 ET-GM-PHD算法原理

ET-GM-PHD跟踪算法通过高斯混合的方法来拟合目标的PHD，令目标状态为：

预测：先验目标的PHD表示为：

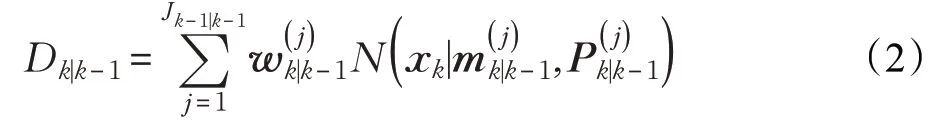
更新：后验目标的PHD通过Dk|k-1来更新，即：

其中，Lzk是伪似然函数，表示为：

其中，γ( )x 是量测数的期望，pD是检测概率，wp是划分权重，φzk是量测空间似然，λk是杂波数均值，ck是杂波空间似然。

2.2 DP-Kmeans++量测集划分算法原理

量测集划分是ET-GM-PHD 跟踪算法中的重要步骤，将量测集Zk分割成有限数量个非空子集W ，即称为一种划分，记做p（为了易于理解，通常在不影响理解的情况下不对W 和p 添加标号）。

DP-Kmeans++划分算法的步骤如下：

步骤1 利用文献[2]中的DP算法，用给定的n 个距离阈值得到n 种划分结果。

步骤2 判定每种划分中的非空子集W 由几个目标产生，判定公式如下：

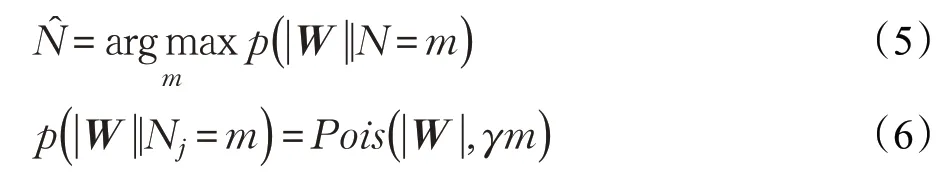
步骤3 若某子集W 对应的大于1，则用Kmeans++算法将W 划分成个子类。

3 DP-TP-Kmeans++量测集划分算法

DP-Kmeans++算法在目标邻近时精度不足，原因是DP 算法和Kmeans++算法都难以正确地分割邻近目标的量测集。因此，本文在两种算法间插入一步基于TP的量测分割算法，提高了原算法的划分精度。

3.1 问题描述与核心思想

DP 算法仅利用量测间彼此距离来分割量测集，因此会将邻近目标的量测聚类为同一子集W 。Kmeans++算法同样容易收敛到错误的分割结果，造成划分失败。DP-Kmeans++算法的主要问题有以下两点：

（1）算法通过公式（5）、（6）来判定W 是否需要进行子划分，但由于目标数量的随机性，有时候两个紧邻目标产生的量测数量仅使N̂=1，造成Kmeans++算法为被启用，划分失败。

（2）Kmeans++算法对紧邻目标的划分时，经常产生如图1 所示的错误收敛现象。图中左上角第一个子图为真实量测结果，椭圆表示两个目标的轮廓；其他子图为迭代过程，黑色圆圈表示类中心，可见划分结果出现严重错误。

针对DP-Kmeans++算法的问题，提出算法保留了DP-Kmeans++算法的步骤。首先，利用DP 算法进行初步划分，区分量测集和杂波集。然后，执行TP 步骤，对于DP 划分结果的量测集，使用目标预测的位置作为聚类中心，预测目标的数量作为类的数量，利用量测与离类中心的距离来进行一步的聚类。最后，对于TP 步骤的聚类结果，再利用公式（5）、（6）对量测数量进行判定，对量测数量过多的量测子集依然使用Kmeans++算法进行分割，进一步保证了提出算法的精度。

3.2 DP-TP-Kmeans++的算法实现

令传感器第k 次探测的量测集表示为Zk，则DPTP-Kmeans++算法可按照下述步骤实现：

步骤1 基于DP算法的初步划分。

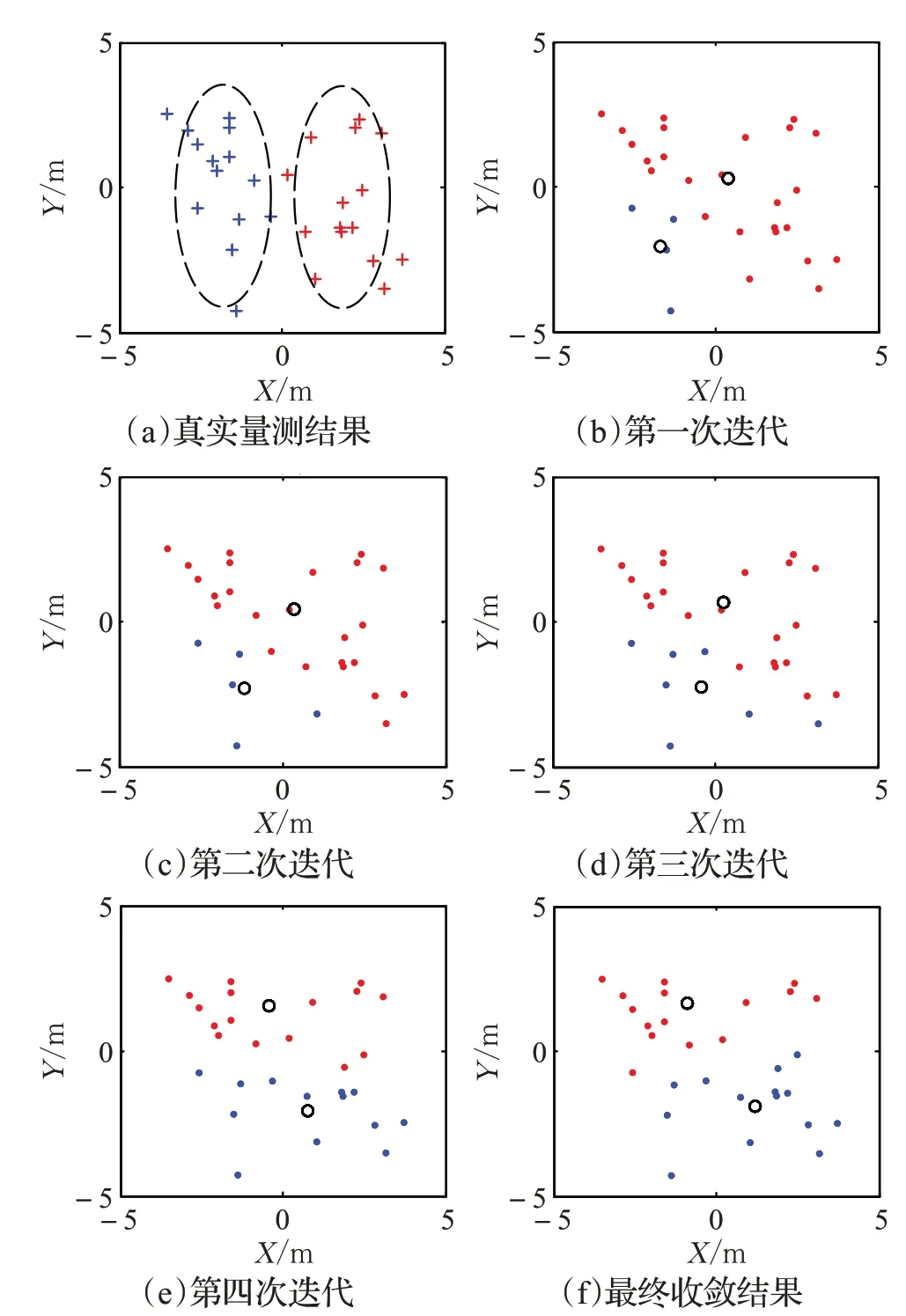
图1 Kmeans++聚类结果

步骤2 基于TP的量测集分割。

令 ||⋅表示集合中元素的数量，则对于划分p 的某量测子集W ，若 ||W =1 则认为是杂波，若 ||W ＞1 则认为是量测。令划分p 中所有杂波组成集合Zclu，所有量测组成集合Zmea。令Jk|k-1表示k 时刻先验目标的数量，表示第j 个目标的预测位置，则Zmea被分割为Jk|k-1个子集，第j 个子集表示为：

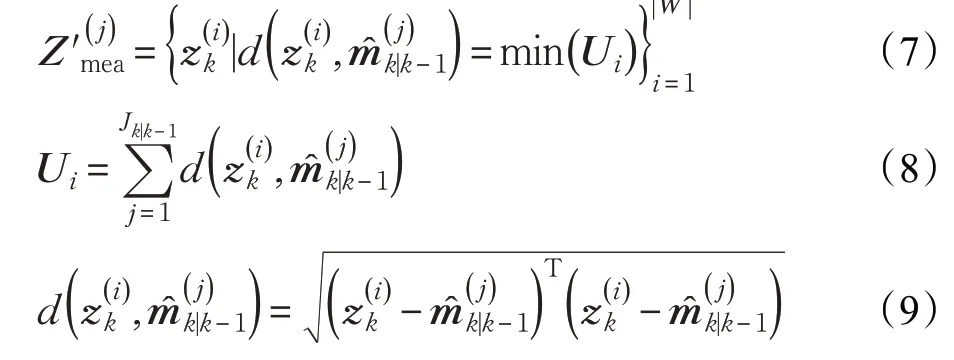
步骤3 基于Kmeans++的特殊量测集分割。

为了在预测目标数不准的情况下保证划分精度，对于步骤2的结果中每个W ，依然需要利用公式（5）、（6）对量测数是否异常来进行检测。若N̂ 大于1，则用Kmeans++算法将对应量测集子分割成N̂个子类。

4 仿真实验

为验证提出算法的有效性，在两组不同的场景中进行了仿真实验。实验环境为：仿真软件：MATLAB 2012a，CPU：Intel®CoreTMi7-6700HQ。不同实验中目标的轨迹如图2所示。图2（a）中目标1和目标2存在时间为1～100 s，目标3 存在时间为21～80 s，目标4 存在时间为41～60 s。图2（b）中两目标的存在时间为1～100 s。

图2 目标轨迹

场景参数设定如下：

其中，Rk表示量测噪声协方差矩阵，表示Qk过程噪声协方差矩阵。S 表示传感器探测面积。λkck表示每帧探测中单位面积的杂波率。场景中传感器的帧间隔为T=1 s。目标存活概率为PS=0.99。传感器检测概率为PD=0.99。

新生目标的参数如下：

其中，m0为目标初始状态，x0和y0表示场景中真实目标的新生坐标。 P0表示目标初始高斯协方差矩阵。初始目标权重为w0=0.1。实验中的跟踪结果误差由OSPA 误差距离[15]进行量化。DP 算法的阈值集合为

为充分验证本文方法的有效性，以文献[13]中SNN-AP方法作为对比实验，从精度和运算代价两个不同维度展示算法的性能。

4.1 多目标交叉场景

本场景目标轨迹如图2（a）所示，共进行了100次蒙特卡洛实验。

图3（a）为100 次实验的平均OSPA 误差距离结果。可以看出，ET-GM-PHD算法使用DP算法进行量测集划分时，在目标邻近时会造成OSPA 误差增大，其原因为DP 算法基于量测间的距离对量测集进行分割，而多目标邻近时彼此量测集也邻近，因此DP 算法失效导致跟踪精度明显下降。DP-Kmeans++作为DP算法的一种改进算法，其在目标邻近时的划分效果明显提高，因此导致目标紧邻时的OSPA误差虽然也明显增加，但远小于DP算法。SNN-AP算法在目标紧邻时的误差值介于DP与DP-Kmeans++之间，其原因是多个目标同时紧邻导致算法的初始化参数不够准确。提出的DP-TP-Kmeans++算法在目标邻近时的OSPA误差略小于DP-Kmeans++，说明提出算法加入的TP步骤有效地增加了邻近目标量测集的划分精度，从而减小了整体跟踪误差。

图3（b）为100 次实验的平均目标数估计结果。可以看出，DP 和SNN-AP 算法在目标邻近时的目标数估计结果明显低于真实值，说明其未能分割邻近目标的量测集，造成目标数漏估计。DP-Kmeans++算法和提出的DP-TP-Kmeans++算法在目标邻近时的目标数估计结果大致相同，且略高于真实值，说明两种算法都可以分割邻近目标的量测集。对比图3（a）结果，说明提出算法优于DP-Kmeans++算法的原因不是势估计的精度提高，是划分结果的精度提高。

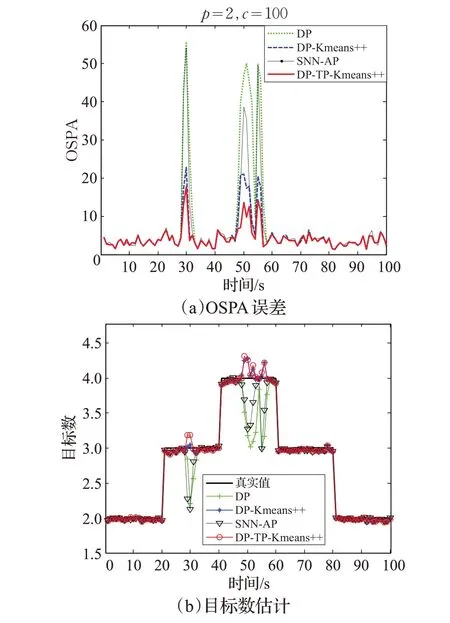
图3 多目标交叉场景100次实验平均结果

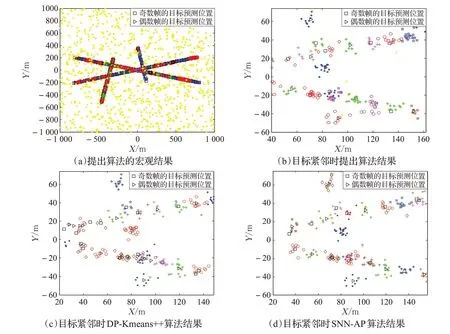
图4 单次实验的划分结果

图4是单次跟踪实验各划分算法的结果图。图4（a）是提出算法划分结果的宏观结果，其中黄色点为提出算法在距离阈值为30时，通过DP算法初步划分得到的杂波，可见利用距离阈值可有效分辨大部分由白噪声产生的杂波。图4（b）是目标1、目标2、目标3紧邻时，阈值取30时提出算法的划分结果。图中用不同符号标出奇、偶数帧的目标预测位置，目的是更清晰地表示出同帧目标的位置。同帧不同的颜色、符号点分别代表不同的量测子集。图中可见提出算法在目标紧邻时能较为正确地根据预测信息划分出量测集。图4（c）是DP-Kmeans++算法在距离阈值为30 时的划分结果，可见多帧出现了目标数的过估计、漏估计显现，在贝叶斯迭代过程中这些错误会向前传递，因此累积的划分错误是造成其目标紧邻时OSPA误差值过大的主要原因。图4（d）是SNN-AP划分的结果，可见大致划分结果与提出方法类似，仅个别帧出现了错误，例如坐标（80，10）附近出现了预测目标的过估计情况（同帧的两个三角形），其原因是上一时刻跟踪系统的状态估计结果不准而导致，说明SNN-AP算法划分精度低于提出算法，导致目标状态估计精度（位置、速度、误差矩阵等）随贝叶斯过程累加降低，有时会出现目标数错估的重大误差，导致EM算法在图3（a）中平均OSPA误差略高于提出算法。

4.2 目标长时间邻近场景

本场景目标轨迹如图2（b）所示，共进行了100次蒙特卡洛实验。

图5 目标长时间邻近场景100次实验平均结果

图5（a）为100次实验的平均OSPA误差结果。可以看出，使用DP算法的OSPA误差远高于其他划分算法，说明其他算法对比DP算法均能有效提高邻近目标量测集的划分精度。SNN-AP算法的误差值与DP-Kmeans++算法大体上相同，说明在两目标紧邻情况下两者的精度基本相同。提出算法的误差略低于SNN-AP 和DPKmeans++算法，说明提出算法在目标长时间邻近情况下依然能保证较高的划分精度。

图5（b）为100 次实验的平均目标数估计结果。可以看出，DP算法导致目标数估计结果低于真实值，说明其会导致目标数漏估计现象发生。DP-Kmeans++算法和提出算法的目标数估计结果大致相同，且略高于真实值，说明其会对邻近目标的量测集进行分割，但有时会发生将两个目标的量测集分割成多个的现象。SNN-AP算法的值明显高于真实值，说明该场景下导致SNN-AP算法精度下降的主要原因是AP算法多度分割了紧邻量测集。

图6为100次实验的平均运算代价结果。运算代价数据的获取方法为在100次的实验中，MATLAB程序中记录划分算法总执行秒数的平均值来获得。可见，SNN-AP算法的运算代价明显小于其他算法；DP算法的时间代价略小于DP-Kmeans++算法；提出的DP-TPKmeans++算法的时间代价明显高于其他三种算法。结合图5 结果，说明在该场景下SNN-AP 算法取得与DPKmeans++相似精度的情况下，可以极大地减小系统的运算代价，适合于对运算速度要求较高的实时跟踪系统。而提出算法在提高了整体精度的同时，也增大了其运算代价，因此提出的DP-TP-Kmeans++算法适合于精度要求较高而对运算代价要求低的跟踪系统。

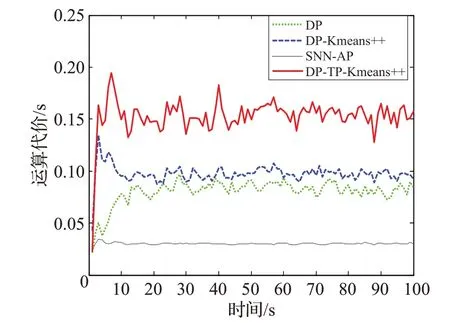
图6 时间代价结果

5 结论

针对扩展目标紧邻时量测集划分精度下降问题，提出了DP-TP-Kmeans++量测集划分算法。创新点如下：

（1）提出利用目标预测信息来划分邻近目标的量测集的方法，提高了划分精度。

（2）结合了DP-Kmeans++算法的步骤，提出DPTP-Kmeans++算法，并应用于ET-GM-PHD算法。

实验结果表明，提出的DP-TP-Kmeans++算法的划分精度高于其他算法，但时间代价也高于其他算法。下一步的工作可以围绕降低提出算法的时间代价展开，以增加提出算法的总体性能。