基于BBS产生器和椭圆曲线的改进RC4算法

陈 虹，刘雨朦，肖成龙，郭鹏飞，肖振久

辽宁工程技术大学 软件学院，辽宁 葫芦岛125105

1 引言

RC4（Rivest Cipher 4）算法是一种在电子信息领域加密的技术手段，由RSA公司在1987年提出，采用由字节流方式产生的密钥流序列对信息进行加密或解密，是密钥长度可变的对称流加密算法。RC4 算法广泛应用于SSL/TLS（Secure Sockets Layer，安全套接层/Transport Layer Security，传输层安全）协议、WEP（Wired Equivalent Privacy，有线等效保密）协议和WPA（Wi-Fi Protected Access，Wi-Fi保护接入）协议等多种网络和数据传输协议。虽然RC4可以加密传输数据，但密钥信息具有不变脆弱性，易被敌手猜测赋值攻击，安全性受到威胁，因此密钥流序列的随机性大小和是否易破解直接影响到RC4算法的安全与否。

RC4 算法易受包括故障引入攻击、区分攻击和“受戒礼”攻击在内的多种攻击。1994 年Finney[1]提出对RC4算法的故障引入攻击，即假设攻击者可获得足够多的PRGA（Pseudo Random Generation Algorithm，伪随机序列生成算法）输出序列并在RC4的运行过程中引入错误，那么根据这些输出序列就可计算出RC4的初始状态，不需要密钥就可以成功破解RC4 的密文。1998 年Knudsen等[2]提出状态猜测攻击。2000年，Fluhrer和Mc Grew[3]通过证明RC4算法密钥流的任意连续两个输出字不独立，给出了对算法的区分攻击。2004年Paul和Preneel[4]提出根据RC4 密钥流前两个输出字节存在的偏差进行区分攻击[5-6]可以恢复算法的初始状态，导致加密信息泄露等严重后果；同年文献[7]提出对RC4算法的错误引入攻击。2013年，Lucky13[8]针对TLS中CBC（Cipher Block Chaining，密码分组链接）模式出现的漏洞对RC4 算法进行攻击。2014年，Shareef等人[9]提出水印和加密是互补的信息安全工具，并在文献[9]中使用RC4 算法加密可变大小的图像，完成了水印和加密算法的组合，认为RC4 是最简单最强大的流密码；Handa[10]和他的团队设计了一种在并行加密大量数据时的并行执行RC4 的方法，命名为PARC4，实验结果表明在实现并行化上效果较好，下一步他们计划研究替代并行化相同算法的技术并测量效率；Jindal P 等人[11]则报告了几个RC4 算法的漏洞并提出了修改的RC4算法MPC4，该算法未修改其基本结构，仅在KSA 和PRGA 部分添加了额外层，结果表明MPC4 算法在增强安全性的同时产生几乎相同的加密时间，但该算法对吞吐量和CPU 负载分析并没有做出分析。2015年，Mantin I利用RC4算法存在的不变性弱密钥[12-15]使RC4 算法陷入了“受戒礼”攻击[15]；同年Vanhoef等在文献[16]中提出一种方法，仅用9×227个密文就可在75 h 内破解采用RC4 加密的存储在用户本地终端上的数据，成功率高达94%。2016年，Liu C等人[17]提出了一种基于大数据处理的新方法分析RC4 安全性的技术，通过演示如何应用大数据分析评估著名的统计特性流密码发现：RC4虽然仍是唯一可用的最安全的流密码协议，但越来越多的证据表明RC4不能提供足够大的安全边距，RC4 算法亟待改进。2018 年，文献[18]提出了对RC4 算法的明文恢复攻击，即高概率对经RC4算法加密的明文的前256字节进行恢复，使RC4算法安全性受到威胁。

本文针对RC4算法易受故障引入攻击、区分攻击和“受戒礼”攻击等导致安全性降低的问题，提出了一种基于椭圆曲线的RC4 改进算法，该算法以随机置换为基础，种子密钥Key 由随机比特产生器产生，同时利用椭圆曲线算法产生的随机整数对状态表进行非线性运算，从而产生用于加解密的流密钥序列。该算法具有不可逆性、高安全性和随机性，能有效抵抗故障引入攻击、区分攻击和“受戒礼”攻击。

2 RC4算法简介

RC4 算法是一种基于非线性变换的流密码算法。从内部结构可分为内部状态S盒、状态变换函数和输出函数，RC4内部状态变化如图1所示。

从运算过程上可分为密钥编制算法KSA和伪随机序列生成算法PRGA。

（1）密钥编制算法KSA（Key Sehedule Algorithm）：设置S盒的初始排列，用长度可变的密钥产生密钥流生成器的初始状态。

（2）伪随机序列生成算法PRGA（Pseudo Random Generation Algorithm）：根据初始状态进行非线性运算，选取随机元素，修改S 盒的原始排列顺序，产生与明文或密文进行非线性运算的密钥流序列。

2.1 密钥编制算法KSA

RC4 的密钥编制算法KSA 用于产生密钥流生成器的初始状态，步骤如下：

步骤1 随机选取一个字长为l 的密钥Key，初始化S盒。

步骤2 指针it遍历S盒中的每一个位置，it每更新一次，jt就会在St-1[it]和Key的作用下产生一个新值。

步骤3 交换St中jt和it对应的两个字节，经过N步遍历即产生RC4的初始状态S0。RC4的密钥编制算法KSA如下所示：

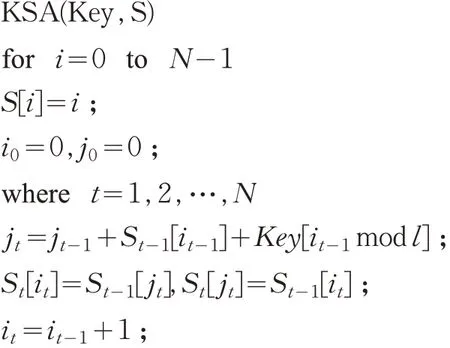
其中，N=256，S盒表示算法的内部状态表，每一个S盒中有N 个8比特值，St表示在t 时刻的状态表，it和jt表示t 时刻的两个指针，指向St中的两个元素。Key表示种子密钥，l 为其长度，l=K 的比特数/n,n 表示算法中使用的一个字节长度，Zt表示t 时刻的密钥流输出字节。

图1 RC4内部状态变化过程

2.2 伪随机序列生成算法PRGA

伪随机序列的生成原理是不断变换S 盒中的元素位置，同时从中选取随机元素输出，即为伪随机序列，构成加解密运算的密钥流序列。伪随机序列生成原理如图2所示。

图2 伪随机序列生成原理

PRGA的步骤如下：

步骤1 根据KSA产生的初始状态表S0，初始化指针it和jt。

步骤2 更新算法中的j，同时交换St中it和jt对应的字节。

步骤3 伪随机序列生成器不断变换S 盒中字节的位置，每次改变后将S中St[it]+St[jt]位置的值输出，即为密钥流输出字节，输出的字节序列是Zt与明文异或加密，与密文异或解密。RC4的伪随机序列生成算法PRGA如下所示：

PRGA(S0)

Initialization：

i0=0

j0=0

while（TRUE）

it=(it-1+1)mod N ；

jt=(jt-1+St-1[it])mod N ；

St[it]=St-1[jt],St[jt]=St-1[it]；

Zt=St[(St[it]+St[jt])mod N]；

output Zt

endwhile

其中，N=256,it,jt表示两个参数，St表示在t 时刻的状态表，Zt表示t 时刻的输出值。加密时，将Zt与明文异或；解密时，将Zt与密文异或。

3 基于BBS和椭圆曲线的改进RC4算法

RC4算法易受错误引入攻击、区分攻击和弱密钥攻击。RC4 的典型改进算法VMPC[19]对RC4 的KSA 部分进行改进，可以灵活选择算法步骤，但密钥流序列随机性不高导致安全性降低。文献[20]利用223输出值将密钥流序列与随机序列区分开，获得了初始状态并破解了文献[19]的VMPC 算法。文献[21]中，在PRGA 部分增加了自我检错步骤抵御状态猜测攻击和错误引入攻击，但密钥字节序列的输出变得复杂，导致效率降低；文献[22]对RC4 算法的密钥流输出序列的偏差规律进行研究，苑超等人[18]借助该规律给出了对RC4算法的明文恢复攻击。

本文提出的基于BBS产生器和椭圆曲线的RC4改进算法同时对KSA 和PRGA 两部分进行改进，以随机置换为基础，借助随机比特产生器和椭圆曲线生成具有高随机性和安全性的密钥流序列。

3.1 改进RC4的密钥编制算法KSA

改进RC4算法的KSA如下所示：

KSA(Key,S)

for i=0 to N-1,a=0 to 30

S[i]=i；

Ba=Xamod 2

Key={B30}

i0=0,j0=0；

where t=1,2,…,N

jt=jt-1+St-1[it-1]+Key[it-1mod l]；

St[it]=St-1[jt],St[jt]=St-1[it]；

it=it-1+1

利用BBS 随机比特产生器产生比特序列作为种子密钥Key进行运算，通过指针进行N步遍历后生成S盒的初始状态S0，步骤如下：

步骤1 从事先准备好的五位大素数库随机选取两个满足条件的素数送入BBS产生器进行运算，生成30位的随机比特数列作为种子密钥Key，初始化S盒。

步骤2 指针it遍历S 盒所有位置，it每一次更新，jt都会在和Key的作用下产生一个新值。

步骤3 交换St中it和jt对应的两个字节，经过N步遍历即产生RC4的初始状态S0。

BBS（Blum-Blum-Shub）产生器是已证明的密码强度最强的伪随机数产生器，它的过程如下：

步骤1 选择两个大素数p,q,满足p ≡q ≡3(mod 4),令e=p×q。

步骤2 选取一个随机数v，使得v 与e 互素。

步骤3 按以下算法产生比特序列{Ba}：

X0=v2mod e

for a=1 to ∞do{

Xa=

Ba=Xamod 2}

即在每次循环中取Xa的最低有效位。

3.2 改进RC4的伪随机序列生成算法PRGA

RC4 算法S 盒中的元素是0～28-1 的全排列，状态表的更新通过交换S盒中的两个元素，前后状态变化不大；同时输出状态仅通过一次交换的操作来更新，易受区分攻击。本文针对上述问题提出的基于BBS产生器和椭圆曲线的RC4 改进算法的伪随机序列生成算法PRGA如下所示：

PRGA（S）

i=0；

j=0；

while（TRUE）

i=(i+1)mod N ；

j=(j+S[i])mod N ；

out=(S[(S[i]+S[j]mod N)+g])mod 256；

S[(S[i]+S[j])mod N]=(g+S[i])mod 256；

改进如下：

（1）采用S 盒前一个状态j 位置值与后一个状态i位置值的和替代当前位置的值，更新状态表。S盒前后状态变化增大，同时确保状态表产生的新元素不依赖S盒中的一个值或几个值。

（2）利用椭圆曲线算法生成秘密整数g ，采用秘密整数与状态表中j 和i 位置的值相加模256的方法生成输出密钥流序列，更新输出状态并确保了输出序列的随机性。

步骤1 获得KSA 初始化的S 盒和秘密整数g ，初始化指针i,j。

步骤2 更新索引指针i 和j，输出两个指针对应的值与g 的和，即(S[S[i]+S[j]mod N]+g)mod 256，其中N=2n。

步骤3 利用g 更新状态表中的元素，即S[(S[i]+S[j])mod N]=(g+S[i])mod 256。

椭圆曲线加密算法（Elliptic Curve Cryptography，ECC）[23-24]是一类以椭圆曲线的数学理论为核心的单向不可逆公钥密码体制，其安全性基于离散对数问题求解的困难性，椭圆曲线密码系统单位比特的高强度使得椭圆曲线密码体制成为目前信息安全领域的核心体制。密码中普遍采用的是有限域上的椭圆曲线，即所有系数都是某一有限域GF(m)中的元素（其中m 为一个大素数）。其中最常用的是由方程y2=x3+ax+b(a,b ∈GF(m),4a3+27b2≠0) 定义的曲线。本文取a=1,b=1 即方程y=x3+x+1 进行运算，其图形是连续曲线，如图3所示，设Gm(1,1)表示方程y=x3+x+1 所定义的椭圆曲线上的点集{ }

(x,y)|0 ≤x ＜m,0 ≤y ＜m,且x,y均为整数 并上无穷远点O（O 为加法单元，即对椭圆曲线上任一点G，有G+O=G）。Gm(1,1)由以下方式产生：

步骤1 对每一x（0 ≤x ＜m 且x 为整数），计算x3+x+1(mod m)。

图3 椭圆曲线y2=x3+x+1 图像

步骤2 判断步骤1中求得的模m 下是否有平方根，如果没有，则曲线上不存在与该x 相对应的点，如果有，则求出两个平方根（y=0 时只有一个平方根）。

按照上述方式GF(m)上的椭圆曲线y2=x3+x+1在第一象限的整数点加无穷远点O 共有1+m+个。本文从五位大素数库中随机取一个作为m 进行运算，从生成的点集Gm(1,1) 中去掉x=0,y=0 和无穷远点，在剩下的点集中随机取一个坐标点，这个坐标点的y 坐标的值即为所需要的秘密整数记为g，进行接下来的运算。

秘密整数g 是由椭圆曲线基于数学上的困难问题——离散对数分解，在有限域上产生单向不可逆的整数产生，本文采用随机选取一个五位大素数的方法来划分椭圆曲线的有限域，增加了秘密整数g 的随机性和破解难度。椭圆曲线选取y=x3+x+1 进行运算，曲线简单，运算速度较快，五位大素数能够满足椭圆曲线有限域的划分需求，其安全性优于四位大素数，速度优于六位大素数，因此，二者结合产生的秘密整数g 增加了随机性和安全性。

3.3 改进的RC4算法

基于椭圆曲线的改进RC4算法借助BBS产生器生成种子密钥Key送入S盒，在指针的作用下N 步遍历后生成S 盒的初始状态S0，利用椭圆曲线产生的整数g更新指针和状态表中的元素，生成用于加解密的密钥流序列。改进RC4算法由密钥编制算法KSA和伪随机序列生成算法PRGA 两部分组成，内部状态如图4 所示，步骤如下：

步骤1 随机取两个五位大素数p,q 送入BBS产生器生成随机比特数列作为种子密钥Key。

步骤2 初始化S盒，在指针作用下遍历S盒生成初始状态S0。

步骤3 随机取五位大素数m 通过椭圆曲线y2=x3+x+1 生成秘密整数g。

步骤4 初始化索引指针i,j，通过g 更新指针和状态表元素，输出密钥流序列。

4 改进RC4算法安全性分析

RC4算法密钥流随机性不高，易被敌手猜测赋值，S盒内部状态被破解等问题使RC4算法安全性降低，遭受多种攻击。本文改进RC4算法针对KSA和PRGA部分进行改进，提高了RC4 算法密钥流的随机性和安全性，通过理论和实验验证改进RC4 算法可有效抵抗故障引入攻击、区分攻击和“受戒礼”攻击。

图4 改进RC4算法的内部状态

4.1 密钥流序列的随机性

密钥流序列的随机性即密钥流中比特之间的相互独立性。随机性越高，攻击者对密文的统计分析难度越大。RC4算法的密钥流序列的随机性有三个影响因素：（1）S 盒中的初始值分布均匀程度；（2）索引指针i,j 分布均匀程度；（3）根据指针输出的结果分布均匀程度。RC4算法的内部状态由一个包含256个字节的S盒和指针i,j 组成，输出的密钥流序列由S 盒中的初始值和指针i,j 决定，输出不重复的值至多Z82个，范围较小，密钥流序列的随机性较差。

（1）理论验证改进RC4算法的密钥流序列随机性

①在KSA过程中，S盒的初始状态由种子密钥Key和指针确定，种子密钥Key 通过BBS 产生器产生，具有高随机性，在指针交换作用下S 盒中256 个元素均匀分布在Z82上。

②在PRGA 过程中，指针i 通过(i+1)mod N 进行更新，指针j 通过j=(j+S[i])mod N 进行更新，索引指针分布均匀；由于S[i]中的值和指针j 分别均匀分布在上，所以(S[i]+S[j])mod N 均匀分布在Z2n上。秘密整数g 通过光滑连续椭圆曲线y2=x3+x+1产生，分布均匀，输出的密钥流序列(S[(S[i]+S[j]mod N)+g])mod 256 也是均匀分布的。因此，每个元素的输出概率是相等的，随机性较高。

（2）实验验证改进RC4算法的密钥流序列随机性

本文密钥流序列的随机性测试采用美国国家标准与技术研究院（National Institute of Standards and Technology，NIST）提供的NIST 统计测试套件[25]完成，Linux是由全球范围的系统软件设计专家在遵守通用公共许可证条款（GPL）的前提下共同开发的符合POSIX标准的类UNIX操作系统。Linux以其源代码公开的特性，广泛用于嵌入式系统中，已经成为抗衡Windows 的实用操作系统[26-27]。本文采用Linux虚拟环境对RC4算法和改进RC4算法的密钥流序列进行测试。测试中，取显著性水平∂=0.01，取256 字节内的密钥，分别输出两种算法的密钥流序列1 048 576 bit，更换随机密钥，产生100 组序列进行测试，密钥流序列随机性测试流程如图5所示。

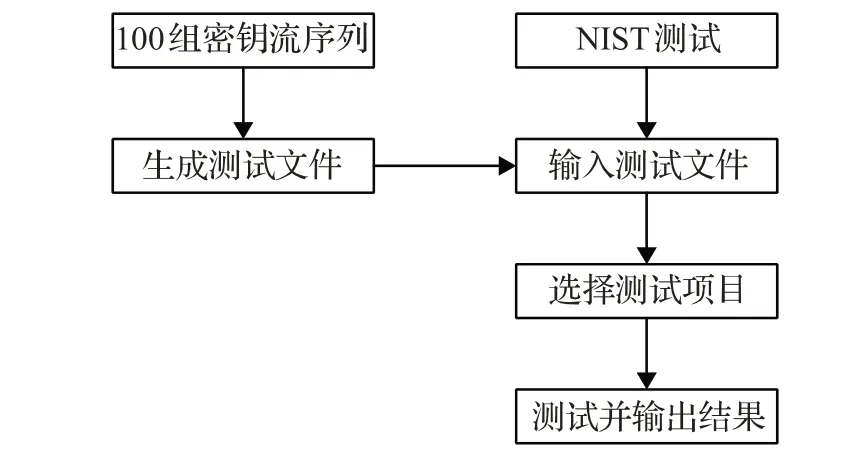
图5 密钥流序列随机性测试流程

步骤如下：

步骤1 产生100 组密钥流序列。将经BBS 产生器产生的种子密钥Key送入S盒生成初始状态，在秘密整数和指针的作用下生成一组密钥流序列，共循环产生100组。

步骤2 生成测试文件。将步骤1中产生的100组密钥流序列以ASCII或二进制形式保存在测试文件中。

步骤3 启动NIST测试平台导入测试文件。在Linux环境下，启动NIST 测试平台，配置参数，并导入步骤2中产生的测试文件。

步骤4 选择测试项目，输入参数后开始测试。在NIST平台中选择频率检验、游程检验、序列检验等16项随机性测试项目，并输入相关参数开始测试。

步骤5 查看测试结果进行分析。

RC4 算法与改进RC4 算法密钥流序列随机性测试结果如表1所示。

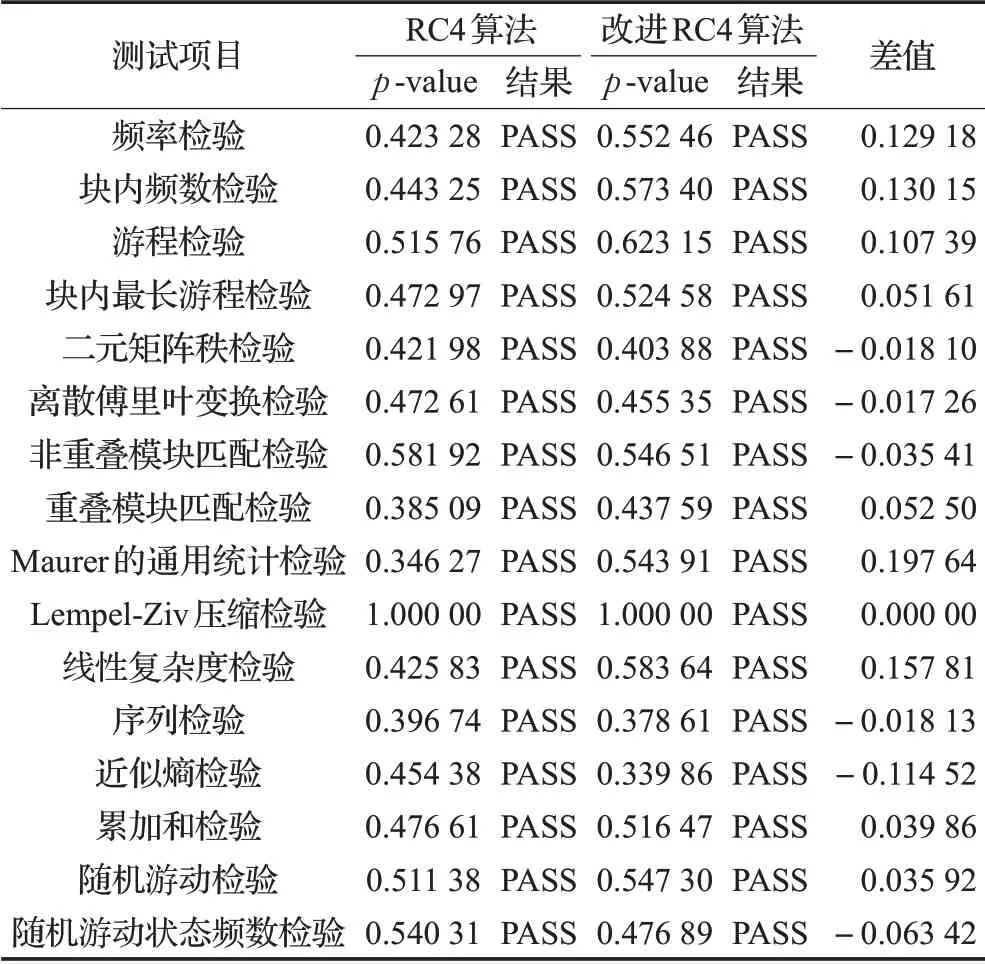
表1 改进RC4与RC4随机性测试结果

表1中p-value是利用卡方分布进行统计分布均匀性的一种指标，测试结果表明，RC4 算法和改进RC4 算法的密钥流序列虽然都能够通过测试，但改进RC4算法检测结果均高于RC4 算法，特别是最重要的3 项测试[28]，频率检验、游程检验和Maurer 的通用统计检验的结果比RC4 算法分别高出0.129 18，0.107 39，0.197 64。因此，改进后RC4 算法的密钥流序列随机性优于RC4算法。这也从密码学统计测试的角度验证了本文改进的RC4算法的随机性和安全性。

4.2 抵抗故障引入攻击

假设攻击者可以获得足够多的PRGA输出序列，然后在RC4的运行过程中引入错误，使其运行进入不可能状态集内，根据这些输出序列，通过分析[21，29-30]就可计算出RC4 的初始状态，那么RC4 的密文不需要密钥就可以成功破解。

Finney[1]对RC4的研究提出一种状态集：{jt=it+1,S[jt]=1},这个状态集有个短的周期((28-1)×28=65 280)，文献[1]指出在RC4算法的运行过程中，由于i0=j0=0，根据短周期和条件jt=it+1 和S[jt]=1，认为这种状态是不可能发生的。Biham 等[29]在RC4 运行过程中的某时刻引入错误，使该时刻的状态进入上面所述的不可能状态集里，进而利用周期性对RC4 的内部状态进行分析，可推测出RC4的初始状态。

分析方法如下：

步骤1 正常运行RC4 算法一次，记录足够多的输出密钥字。

步骤2 重新运行RC4 算法，在it和jt更新为it+1和jt+1且Swap(St[it+1],St[jt+1])未执行前，向S盒的第t个位置引入错误，记录第一个错误的输出时刻T′。

步骤3 重新运行RC4算法，在it-1和jt-1更新为it和jt且Swap(St-1[it],St-1[jt])未执行前，向S 盒的第t个位置引入错误，记录引入错误后得到的第t 个输出密钥字为Z′t和正确的第t 个输出密钥字为Zt。

步骤4 通过判断故障引入攻击后产生的错误密钥字的类型，就可以成功地找出初始状态的值。

由上述步骤可知，错误引入攻击是在PRGA阶段交换操作之前且S盒中的元素不变的条件下实施的，由于改进RC4算法增加一个秘密整数g ，在每次输出之后，利用g 对S盒中的元素重新赋值S[(S[i]+S[j])mod N]=(g+S[i])mod 256，并没有出现交换操作，且在指针和秘密整数的作用下S盒中的元素是不断被更新的，即使在运行过程中向S盒的t 位置引入错误元素，也不能确定t 位置的值，因此，基于Finney状态的故障引入攻击方法对改进RC4 算法无效，即改进RC4 算法可以抵抗故障引入攻击。

4.3 抵抗区分攻击

区分攻击主要通过检查由密钥编制算法KSA引起的偏差或影响密钥流初始化的其他特点所引起的偏差进行攻击。

（1）抵抗内部状态分布均匀的区分攻击

Mantin 和Shamir 在文献[31]中提出了对RC4 算法的区分攻击，他们假设算法在经过KSA 部分后所得到的内部状态是独立且分布均匀的，通过研究RC4密钥流的输出序列发现以下现象：①RC4 密钥流的第二个输出字值是0 的概率为2/N ，如果S0[2]=0 且S0[1]≠2，则第二个输出值为0 的概率约为1，即P[Z2=0]≈1。②RC4密钥流第一个输出字为0的概率为3/N2。由于这些分析，RC4算法遭受区分攻击，安全性受到威胁。

然而在改进RC4 算法中，输出值为(S[(S[i]+S[j])mod N]+g)mod 256，由指针和椭圆曲线生成的秘密整数g 共同确定，无法预知，即使S0[2]=0 且S0[1]≠2，由于g 分布均匀且是秘密数，不会出现概率偏差的情况，Mantin's区分攻击所依靠的两个概率对改进RC4算法并不适用，无法对改进RC4 算法进行攻击，即改进RC4算法可以抵抗内部状态分布均匀的区分攻击。

（2）抵抗内部状态分布不均的区分攻击

文献[12]证明RC4 算法在KSA 部分所得的内部状态分布不均，Paul和Preneel又在文献[4]中指出，RC4密钥流前两个输出字节存在偏差，根据这个偏差进行区分攻击只需要226字节就可以恢复RC4 算法的初始状态S0。而后常亚勤又在文献[6]中证明了密钥流的第1 个输出字节分布不均匀，将区分攻击改进为只要224字节就可恢复初始状态S0。而在本文改进RC4 算法中，KSA部分所得的内部状态分布均匀，不存在这些偏差，因此这些攻击无效。

RC4算法区分攻击的原理如下：

定理1 记P(SN[u]=v)为RC4算法在经过KSA 后，数组SN输入为u、输出为v 的概率[5]，为保证数据不存在偏差，其计算条件为i=0,j=j+S[i],Swap(S[i],S[j]),则：

①当u+1 ≤v ≤N-1 时，有：

其中：

②当v ≤u ≤N-1 时，有：

定理2 RC4 算法密钥流输出的第1个字节Z1的概率为：

对于所有的d(0 ≤d ≤255)，根据定理1 和定理2 可以计算出P(Z1=d)，即理论值Pd。文献[14]利用232个随机密钥产生RC4密钥流的第一个字节进行统计，得到了理论值和实验值结果相同。可见，对于RC4算法的区分攻击只是时间问题，RC4 的初始状态S0总是会被恢复的。

本文改进的RC4 算法抵抗Paul's 区分攻击分为两方面：

（1）定理1 中计算P(SN[u]=v)的公式适用条件为：i=0,j=j+S[i],Swap(S[i],S[j])。本文改进的RC4 算法中，产生的密钥流序列由Key、指针S[i]、S[j]和秘密整数g 共同确定，即使满足上述条件，由于g 是由椭圆曲线产生的一个秘密生成的随机数且均匀分布，不能得出前两个输出字节存在偏差，因此定理1 中公式对改进RC4算法不适用。

（2）改进RC4 算法的Key 由BBS 产生器产生，BBS的安全性基于大整数分阶段困难性，产生的比特序列具有秘密随机的特性，定理1、2中数组SN输入固定值、输出固定值的概率不能确定，第一个输出字为一特定值的概率不能计算，定理1、2不适用于改进RC4算法。

改进RC4 算法的密钥流序列的随机性高于RC4 算法，对改进RC4算法的区分攻击所需要字节数高于RC4算法，耗时长于RC4算法，但密钥流序列具有时效性，在有效时长内区分攻击无法对改进RC4 算法进行有效攻击，因此区分攻击的攻击方法对改进RC4 算法是无效的，即改进RC4算法能够有效抵抗内部状态分布不均的区分攻击。

4.4 抵抗“受戒礼”攻击

“受戒礼”攻击是指利用不变性弱密钥进行的攻击，攻击者通过嗅探监听大量的SSL链接，判断出第一个加密消息包含SSL 的完成消息和HTTP 请求的可预测的信息，当等到一个不变性弱密钥的链接时，一旦明文和这个弱密钥进行异或，攻击者就可以看到生成的密文模式，异或后可获得相应的明文。

改进RC4 算法中，密钥流序列由Key、指针和秘密整数g 共同确定，秘密整数g 由椭圆曲线和五位随机大素数确定，随机性很高，攻击者很难获得可预测信息；改进PRGA中采用S盒前一个状态j 位置值与后一个状态i 位置值的和替代当前位置的值，使得S 盒前后状态变化增大，产生的新元素不依赖S 盒中的一个值或几个值，密钥流序列变化性提高，不存在不变性弱密钥，改进RC4算法可有效抵抗“受戒礼”攻击。

文献[13]中分析了RC4算法中KSA的输出值，发现不变性弱密钥是一个L型图案，这部分密钥可能表现出非随机的特性，攻击者根据这些特性探测出完整密钥从而进行攻击。通过统计状态表S盒内的元素发现，值X在KSA过程结束后出现在状态S中的位置Y 的概率是：

其中，Y′=N-1-Y,p=1/256,q=1-p。尤其值1出现在0位置的概率比随机概率1/N 高37%，值255出现在0位置的概率却比随机概率小26%。攻击者利用这些分析结合N 轮之后的PRGA，也可以恢复密钥。

在改进的RC4 算法中，上述问题很难发生。满足P[S0[Y]=X]的条件是：（1）若X=Si[1]且Y=Si[X]则i ＞1,i ≥X,i ≥X+Y ，其中i 时刻S[X]的状态用Si[X]表示。（2）攻击者必须知道S[1],S[X]和S[X+Y]的值。改进RC4 算法对KSA 部分进行改进，利用BBS 产生器和两个随机的五位大素数生成30位比特序列作为种子密钥Key，BBS 产生器密码强度高，已知一个比特序列的前k 个比特，不存在实际可行的算法能以大于的概率预测下一个比特是0 还是1，即BBS 产生的比特序列无法预测，Key 无法被破解，i ≥1 时的下一次迭代后的状态和S[1]的值也无法获知，不满足上述概率，密钥无法恢复。所以“受戒礼”攻击对改进RC4算法无效，即改进RC4算法可以抵抗“受戒礼”攻击。

5 结束语

本文提出一种基于椭圆曲线的改进RC4算法，该算法借助随机大素数和随机比特产生器生成种子密钥Key，在椭圆曲线生成的秘密整数和指针的作用下进行非线性变换最终生成了随机性和安全性很高的密钥流序列。该密钥流序列由BBS产生器产生的种子Key、大素数、指针i,j 和椭圆曲线生成的秘密整数共同确定，由NIST 随机性测试的频率检验、游程检验和Maurer 等结果可知，改进RC4 算法比RC4 算法分别高出0.129 18，0.107 39，0.197 64，因此，该算法密钥流随机性高于RC4算法，能够有效防止不变性弱密钥的产生，抵抗“受戒礼”攻击。Key是一个分布均匀的随机数，不存在偏差，能够有效抵御区分攻击。椭圆曲线具有单向不可逆性，秘密整数g 无法获知，S 盒内部状态不断变化且未知，能够抵抗故障引入攻击。安全性理论和随机性实验表明改进RC4算法的安全性和随机性高于RC4算法。本文在状态猜测攻击和明文恢复攻击等方面未进行有效测试和验证，这些将是下一步研究工作的方向。