大规模MIMO系统中优化导频分配方案研究

瞿拓思，曹海燕，许方敏，方 昕，王秀敏

1.杭州电子科技大学 通信工程学院，杭州310018

2.中国计量大学 信息工程学院，杭州310018

1 引言

大规模MIMO系统作为5G无线通信标准的关键技术，近年来已经得到学术界和工业界的广泛研究[1-2]。通过在基站端配置大量天线来服务于多个用户，大规模MIMO 技术能增加系统容量，提升能量效率和频谱效率[3]。由随机矩阵理论分析可知，小区间干扰和噪声干扰也能随着基站天线数趋于无穷而避免。但由于导频数量限制会使相邻小区复用一套导频，从而引起的导频污染问题，已经成为大规模MIMO系统性能的瓶颈[1]。

为减轻导频污染的影响，一些研究方案相继被提出[4-8]。在文献[4]中，利用相邻小区间的异步传输设计的时移导频分配是一种有效的解决方案，但会导致数据和导频间的相互干扰。文献[5]中的预编码方案通过多小区联合处理来减轻小区间的干扰，但会造成频谱效率损失。文献[6]提出基于GC（Graph Coloring，图着色）的导频分配方案，结合图论来实现相互干扰小区间的导频分配，有效减少了导频污染。文献[7]则提供了一种依据协方差矩阵的基于空间正交的贪婪导频分配算法，消除了大量天线的导频污染效应，但复杂度大大提高。文献[8]研究了三种导频调度策略使系统可达和速率最大化，分别是基于GA（Greedy Algorithm，贪婪算法）、基于TSA（Tabu Search Algorithm，禁忌搜索算法）和基于GTSA（Greedy and Tabu Search Algorithm，贪婪禁忌搜索算法）的导频调度方案，并给出了一种基于空间正交的贪婪调度算法实现复杂度和性能的折衷。

在文献[8]基于局部搜索算法来获取系统最大可达和速率基础上，本文提出基于IGTSA（Improved Greedy and Tabu Search Algorithm，改进贪婪禁忌搜素算法）的导频分配方案和基于CA（Competition Algorithm，竞争算法）思想的导频分配方案来改善TDD（Time Division Duplex，时分双工）系统中的导频污染问题。前者通过将遗传算法[9]中变异操作引入来扩大搜索空间，优化系统性能。而后者作为人工智能算法，已经在一些领域得到应用[10-11]。本文中的基于CA 思想的导频分配方案则为搜寻系统最大可达和速率提供了有效的优化工具。仿真结果和分析显示该分配方案在性能接近最优的穷尽分配的情况下同时具有更低的复杂度。

2 系统模型

考虑小区数为L 的大规模MIMO 蜂窝通信系统，每个小区内有配置M 根天线的基站和K 个随机分布的用户。每小区共享时频资源并有相同的小区半径。

2.1 信道模型

在大规模MIMO通信系统中，第i 个小区基站的接收信号可以表示为：

其中，ρu为每个用户的平均发射功率，Gil为l 小区中K 个用户到i 小区基站的信道矩阵，xl为l 小区中K个用户的发射数据，而ni为独立加性高斯白噪声。

信道矩阵Gil由下式给出[12]：

其中，Hil表示小尺度衰落系数矩阵，而Dil则为大尺度衰落系数的K×K 维对角矩阵。系数能由下式得到：

其中，himlk为i 小区基站第m 根天线和l 小区第k 个用户之间的小尺度衰落系数，而βilk表示i 小区基站和l小区第k 个用户之间的大尺度衰落系数。

2.2 信道估计

因为上下行链路之间的互易性，TDD大规模MIMO系统在每个相干间隔时间内分为三个阶段。首先，所有的用户都将其导频序列发送到相应基站。上行信道矩阵可由此接收导频信号估计出来。然后用户端再发送上行数据并在基站端通过估计出的信道进行处理。最后，基站依据估计出的结果对下行数据进行预编码，并发送给用户。Φl=[φ1φ2…φk]T∈CK×τ为l 小区中分配给k 个用户的导频矩阵，τ 代表导频序列长度。所以第i 个基站接收导频矩阵的信号可表示为：

其中ρp=τρu，并且Ni是独立加性高斯白噪声矩阵。则最小二乘信道估计矩阵可以表示为[13]：

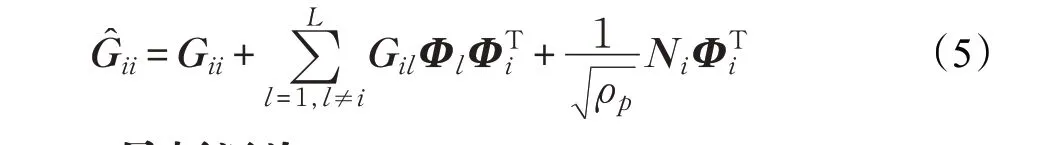
2.3 导频污染

由于在大规模MIMO系统中导频资源有限，相同小区的用户才能被分配正交导频，相邻小区中的用户只能复用同一组导频，这使基站端估计结果受到其他信道分量影响。而这种影响无法通过在基站端提升天线数来解决，极大地制约了通信系统的性能。假设所有小区中用户复用同一套导频，则第i 小区第k 个用户上行信干噪比在基站天线数趋近于无穷时可以表示为[14]：

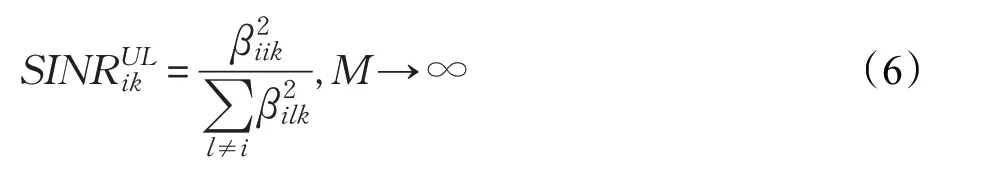
2.4 导频分配索引矩阵

假设相同的K 个导频序列在L 个小区中复用并在同一小区的用户分配互相正交的导频序列。用Uk代表分配第k 个导频序列的用户集合其中代表在l 小区中分配第k 个导频序列的用户。所以导频的分配矩阵[8]如表1 所示，其中pl表示第l 小区的分配情况。以最大可达和速率为性能评判标准来寻找最优导频分配索引矩阵。

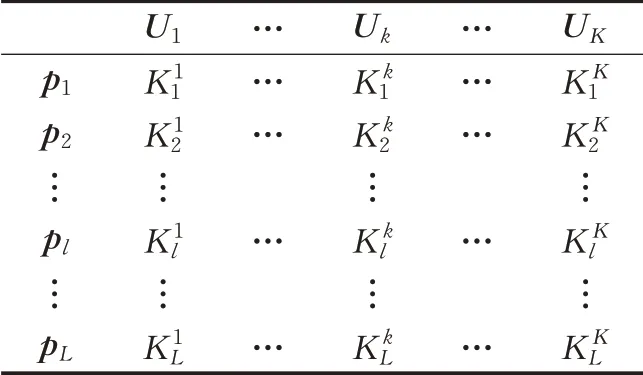
表1 导频分配索引矩阵

3 优化导频分配方案

3.1 IGTSA

禁忌搜索[15]算法主要思想是通过设置禁忌表来记录搜索过程，在下一步的搜索中避开禁忌表中已搜索点。一旦搜索进入局部极值点所在范围内就会以类似爬坡的方式迅速收敛到该点，但一旦陷入局部最优解后，算法如果想要退出并进一步搜寻全局最优解的话，只能通过禁忌表中的记录信息来避开已搜索点，因此算法性能主要取决于禁忌表长度的选定。

为减轻算法对禁忌表候选集大小的依赖，本文引进遗传算法[9]中的变异操作来扩大搜索空间。在基于GTSA的导频分配方案[8]基础上，每一次以小区分配方案为迭代目标时，计算得到其邻域解中的最优目标函数值后加入变异运算达到改进全局搜索能力的目的。本文提出基于IGTSA的导频分配方案。

3.2 基于IGTSA的导频分配方案

把表1中pl作为寻优目标，分不同小区处理。第l小区的用户可达和速率可以由下式得到：

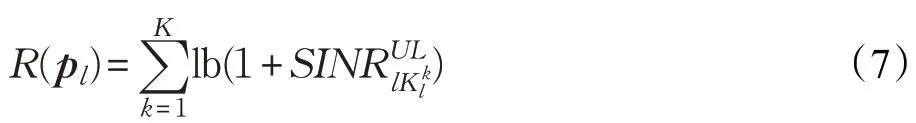
所以最终的分配方案可以表示为：

其中poptl 表示l 小区的最优分配方案，并给出以下定义[8]：

（1）领域定义：定义N(p)表示维度为K 的向量p的领域，即p 中任意两个元素交换位置。

（2）禁忌表定义：设定一个维度为Nt的存储表来存放前几次搜索结果，当表满时剔除表中第一个元素，被删除元素重新成为备选解。

（3）适应度函数定义：

（4）特设准则：定义变量z 记录搜索进程中当前最大目标函数值，如果新目标函数值比z 大，不管其是否在禁忌表中都对z 进行更新。

在此基础上，本文引入变异运算，在导频分配场景下设计如下：

设定ω 为变异标记，Pi为第i 代变异概率，Pset为变异概率阈值，有如下机制：

另设Q 记录z 保持不变的代数，Qset为代数阈值。当Q ＞Qset时，执行变异操作，设向量p 中元素为tk，即将p 中元素作如下改变：

（1）将p(t1)保存至临时变量temp 中。

（2）依次把p(tk+1)的值赋给p(tk)。

（3）将temp 中的值赋给p(tK)。

变异运算具体过程如图1。

基于IGTSA的导频分配方案步骤如下：

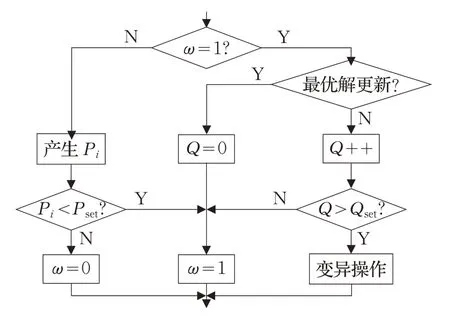
图1 变异运算流程

步骤1 先给出所有用户大尺度衰落系数βilk，其中j,l={1,2,…,L},k={1,2,…,K}。

步骤2 先由GA 算法生成初始分配矩阵[8]，令小区标记l=0。

步骤3 l=l+1，当l ＞L 时终止算法，并输出历史最优解和最优分配方案，否则进入步骤4。

步骤4 当前迭代值为l 小区的分配向量pl，历史最优分配向量记为p*以及最优目标值函数记为ζ=f(I)。设置长度为Nt的空禁忌表，以及算法迭代次数Ts=0，给定迭代次数上限Tset，变异概率阈值Pset和不变代数阈值Qset，变异标记ω 置零。

步骤5 令Ts=Ts+1,如果Ts＞Tset,则记I(l,:)=p*,转至步骤3。否则进入步骤6。

步骤6 对迭代向量的C2K种邻域解计算目标函数并取出最优解pe以及对应分配方案Ie，如果对应目标函数值ζe＞ζ ，则满足特设准则，对ζ 以及p*进行更新并将pe存入禁忌表，否则仅将当前邻域中不包含在禁忌表中的最优解存入禁忌表，转入步骤7。

步骤7 依据图1步骤，进行变异运算，转至步骤5。

改进禁忌算法虽然能扩大搜索空间，避免陷入局部最优解，但其全局搜索能力仍然有待加强。所以本文又提出一种基于CA思想的导频分配方案，达到局部搜索和全局搜索能力的相对均衡，以求进一步提高系统性能。

3.3 CA

近些年来，为更好地解决优化问题，粒子群算法[16-17]、蚁群算法[18]、狼群算法[19-20]等模拟自然现象的群智能全局搜索算法相继被提出并应用到实际中。这类算法在大规模优化问题的求解上相比局部搜索算法有明显优势，能大大提高搜索性能。与这些仿生智能算法相比，CA[11]不但有较强的全局收敛性，还能在较优区域保证算法的局部搜索能力。算法通过分配不同的竞争推动力，达到局部搜索和全局搜索的相对均衡。

利用CA 算法原理，并将每种导频分配方案看成个体组成原始种群，对按目标适应函数进行排序的个体分配不同比例的搜索范围，对处在排序前列的个体分配较小的搜寻空间，对处在排序末尾的个体分配较大的搜寻空间，来增大末尾个体的竞争力。通过竞争的方式保留优秀个体直到搜寻空间逐渐收敛到一个点，也就是算法所求的最优解。在此基础上本文提出基于CA的导频分配方案。

3.4 基于CA的导频分配方案

由于导频分配方案寻优问题并不是连续空间的优化问题，所以本文采用二进制编码[21]来实现离散解空间的寻优，并设定反置操作以及运动算子，假设二进制编码序列集合，则有反置操作：

运动算子：设定θ(B,R,r)为运动算子，其中R 表示反置的编码位集合且不为空，r 表示反置位数，即R 集合元素个数，也被视作分配方案中个体移动步长。

在此基础上引入竞争思想[11]，并依据仿生算法中种群概念[19]，将不同导频分配方案看成个体，依据个体适应度函数值差异来分配不同步长，提出一种基于CA思想的导频分配方案，详细步骤如下：

步骤1 初始化参数，设定种群大小N ，算法迭代次数T 和最大迭代次数Tmax，方向探寻次数S 和最大方向探寻次数Smax，这里的方向指算法搜索方向，历史最优目标函数解Ropt。随机初始化N 组导频分配方案，每种方案表示一个初始种群个体X0i,i ∈{1,2,…,N} ，即有，其中表示l 小区初始分配方案，p0lk为l 小区初始分配第k 个导频序列的用户，个体随着迭代次数更新成

步骤2 将初始个体转换为二进制编码形式，l 小区的初始导频方案对应转换为二进制编码序为编码长度，初始个体转化为

步骤3 判断T ＞Tmax，是则执行步骤8，否则执行步骤4，T=T+1。

步骤4 目标值函数和步长分配概率，每个个体对应分配方案的目标值函数可由以下公式求出：

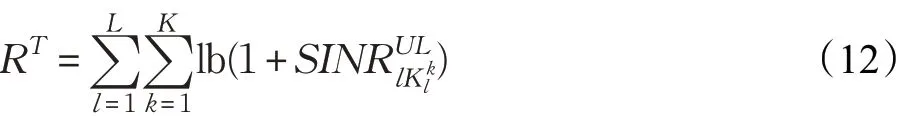
步骤5 分配搜索步长，步长计算公式设定如下：

其中■■为向上取整符号，种群中适应度函数相对小的个体会分配较大步长 从而获得更大搜索空间，以加强全局搜索能力与性能优异个体进行竞争，反之性能优异个体会分配相对较小的步长缩小搜索范围，通过局部精细搜索进一步搜寻更优解。所以个体对应步长为

步骤6 判断S ＞Smax，是则得到更新后种群VT1*,，并求出最优个体对应适应值函数，再判断是否，是则更新历史最优解Ropt，并将VT

1*,代入执行步骤3。如果S ≤Smax，执行步骤7，S=S+1。

步骤7 根据步长随机生成对应长度的反置编码位集合R1,R2,…,RN，并对个体V1,V2,…,VN的相应编码位进行反置操作，然后计算对应的目标函数值，如果则更新个体Vi,否则保持不变，并返回步骤6。

步骤8 算法结束，历史最优解Ropt对应个体为进行解码操作得出个体对应分配方案

4 仿真结果与复杂度分析

考虑到L 小区K 个用户的系统复杂度，穷尽算法需要计算(K!)L-1次可达和速率，而文献[8]中给出的GTSA 的计算次数则为为TSA 迭代次数）。本文提出的两种分配方案，第一种改进禁忌算法虽然在算法过程中增加变异操作，但可达和速率计算次数并未增加，所以即使在GTSA 基础上改进为IGTSA，复杂度依然为。第二种基于CA思想的导频分配方案则需要计算S×T×N 次，因为S，T 和N 都是算法设定参数，所以其他算法随系统总用户数增加导致计算复杂度大大增加时，基于CA思想的导频分配方案的复杂度优势也会得到体现。

设多小区多用户的大规模MIMO 系统中小区直径为1 600 m，路径损耗3.8 dB，阴影衰落8 dB。图2和图3分别给出了理想状况下（天线数趋于无穷）和实际情况下（天线数M=256）基于GTSA、IGTSA、CA 分配以及随机分配和穷尽分配的平均可达和速率的CDF（Cumulative Distribution Function，累积分布函数）比较。可以看出，随机分配的性能最差，基于GTSA 分配相比随机分配在性能上有了很大提升，加入变异操作的IGTSA分配全局搜索能力的增强体现在性能的提升上，而基于CA 思想的分配方案更进一步提升了系统性能，逼近性能最好的穷尽算法，并且复杂度远低于穷尽算法。另一方面，随着系统中小区数和用户数增加，CA分配方案相对于GTSA、IGTSA 分配的复杂度优势也会体现出来。所以仿真结果表明，基于IGTSA 和CA思想的导频分配方案能有效地减轻导频污染对系统性能的影响，而后者不仅在性能上接近穷尽算法，复杂度方面的优势也比较明显。

图2 理想情况中不同导频分配方案下平均可达和速率的CDF

图3 实际情况中不同导频分配方案下平均可达和速率的CDF

为更直观地看出系统趋近于理想情况下性能的变化，图4则给出了小区上行可达和速率随天线数增加的变化情况，可以看出当天线数较少的情况下，非导频污染干扰（多用户干扰和噪声干扰）对系统性能影响较大，使系统的可达和速率被极大地制约。而随着天线数逐渐增加，系统趋近于理想状态，非导频污染干扰的影响随之减小，系统性能在天线数上升初期得到明显提升，但随着天线数趋于无穷，导频污染的存在使系统性能的提升越来越小，最后趋于平稳，接近一个渐进值，所以说导频污染是制约系统性能的关键问题。从图中也能看出，基于IGTSA和CA思想的导频分配方案提升了小区上行可达和速率，减少了导频污染影响。

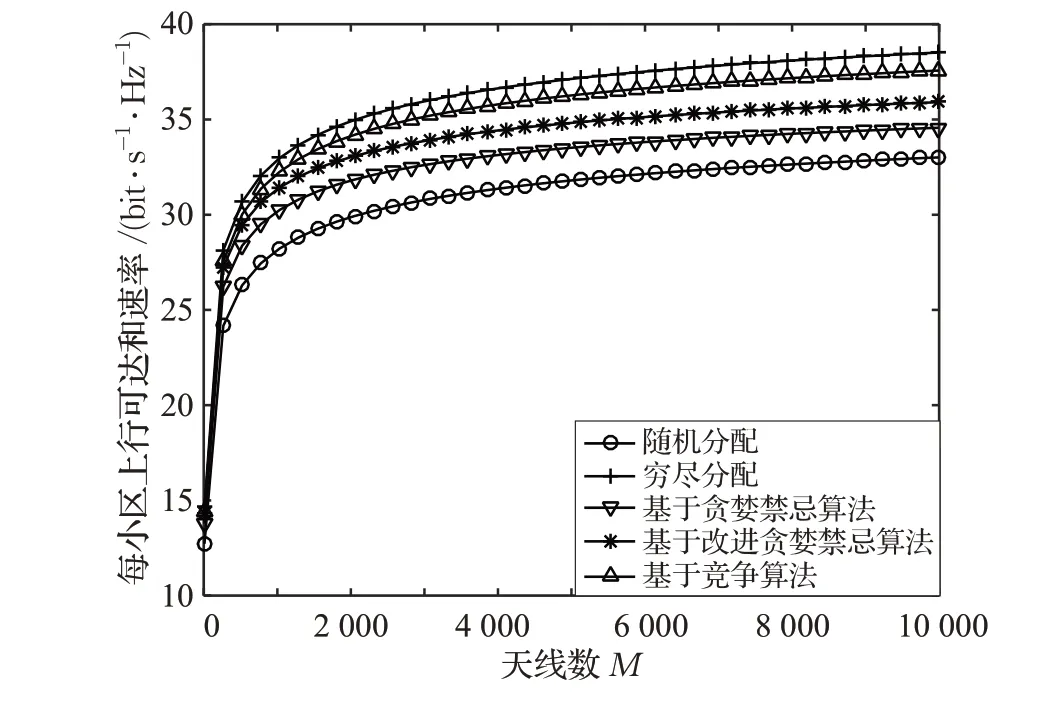
图4 不同导频分配方案下小区上行可达和速率随着天线数变化的情况

为进一步证明基于CA思想的分配方案在减少导频污染以及提高性能方面的优越性，给出其与随机分配方案系统平均速率之差的CDF。如图5 和图6 所示，基于CA思想的分配方案的平均可达和速率明显高于随机分配的平均可达和速率，说明了其对系统性能的有效提升。如图5中，当小区数为4时，所提算法对系统性能的提高随着用户数的增长而增长；在图6中，当用户数为4时，所提算法对系统性能的提高随着小区数的增加而增加。可以得出结论，当系统的整体用户数增加时，基于CA 思想的导频分配方案带来的系统增益也会增加，体现了其在改善导频污染问题方面的有效性和优越性。

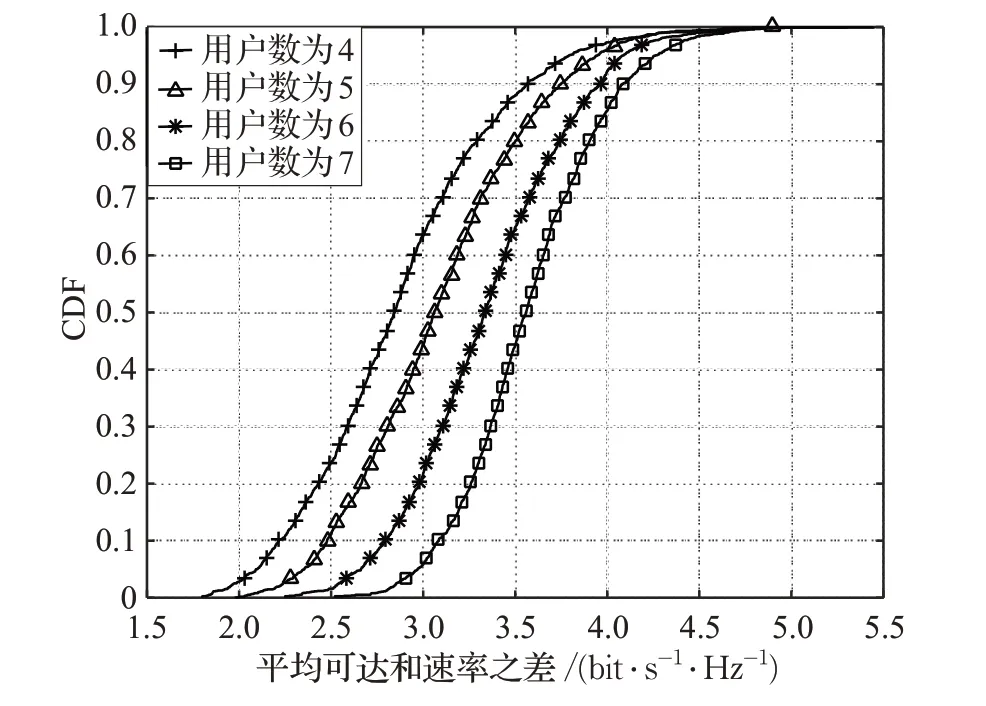
图5 小区数为4时，不同用户数下基于CA分配和随机分配的平均可达和速率之差的CDF比较

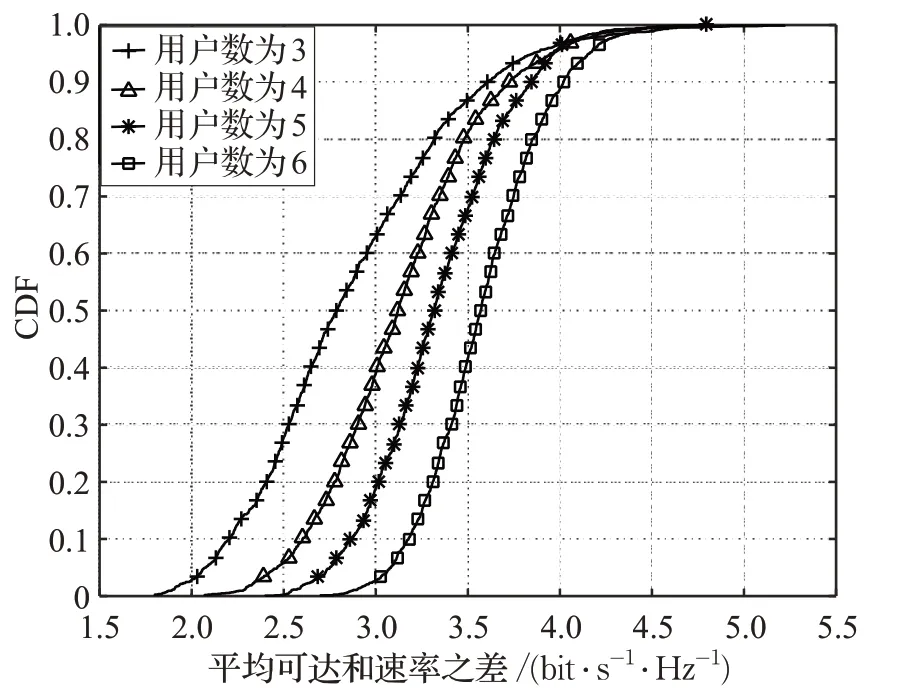
图6 用户数为4 时，不同小区数下基于CA分配和随机算法的平均可达和速率之差的CDF比较

由公式（5）可知，分配方案的不同将会对信道估计产生影响，所以图7 给出不同分配方案下LS 信道估计的最小均方误差变化情况。由图可见，穷尽导频分配方案的均方误差最小，相对应随机分配的性能最差，而基于IGTSA 和CA 思想的分配方案相比除穷尽算法以外的分配方案仍然显示出较强性能优势，亦可见所提方案在改善信道估计性能方面的有效性。

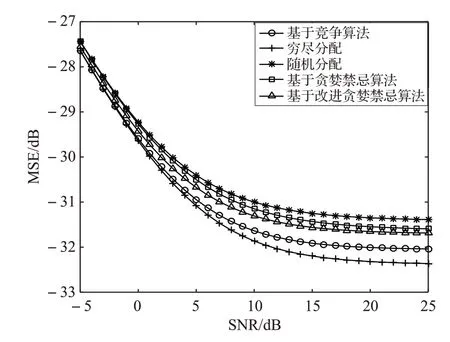
图7 不同导频分配方案下LS信道估计的最小均方误差随SNR变化而变化的情况

5 结语

本文提出了基于IGTSA 和CA 思想的导频分配方案来减轻大规模MIMO系统中的导频污染问题，提高了系统的最大可达和速率。基于IGTSA的导频分配方案在不增加GTSA 分配的复杂度情况下利用变异操作增强全局搜索能力从而获得更优性能。而通过CA算法思想来进一步实现导频最优分配，充分利用算法自身特点，突破局部最优解的限制，在追求用户平均速率更优的同时降低复杂度，仿真结果和分析表明了其算法性能可以接近穷尽算法并在复杂度方面拥有优势。